AdaFlow: Imitation Learning with Variance-Adaptive Flow-Based Policies

↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in robotics and machine learning due to its novel approach to imitation learning. AdaFlow’s fast inference speed and high performance, achieved without sacrificing diversity, address a major bottleneck in current IL methods. This opens avenues for real-world applications of complex, non-declarative robot behaviors where quick responses are essential, impacting fields such as autonomous navigation and manipulation. The theoretical analysis of the ODE discretization error is also a significant contribution, advancing the understanding of flow-based models.

Visual Insights

#

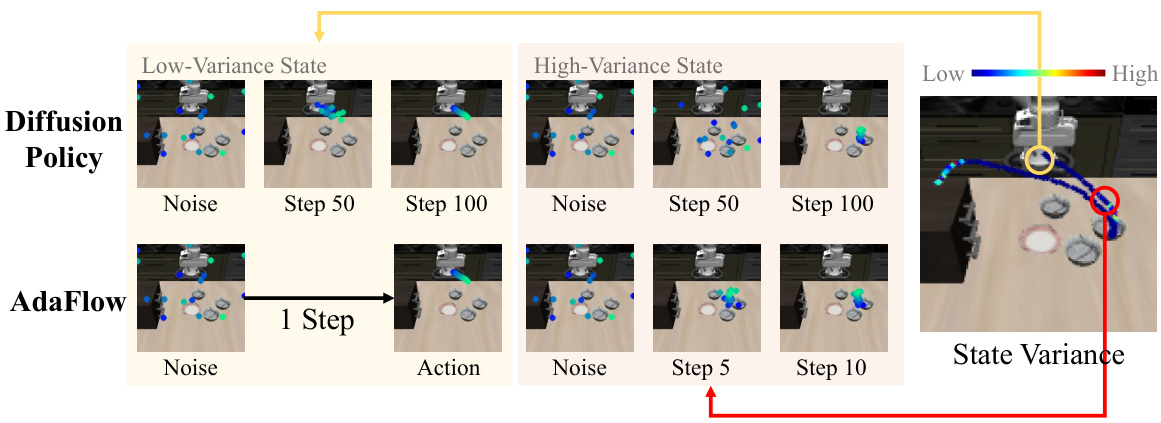
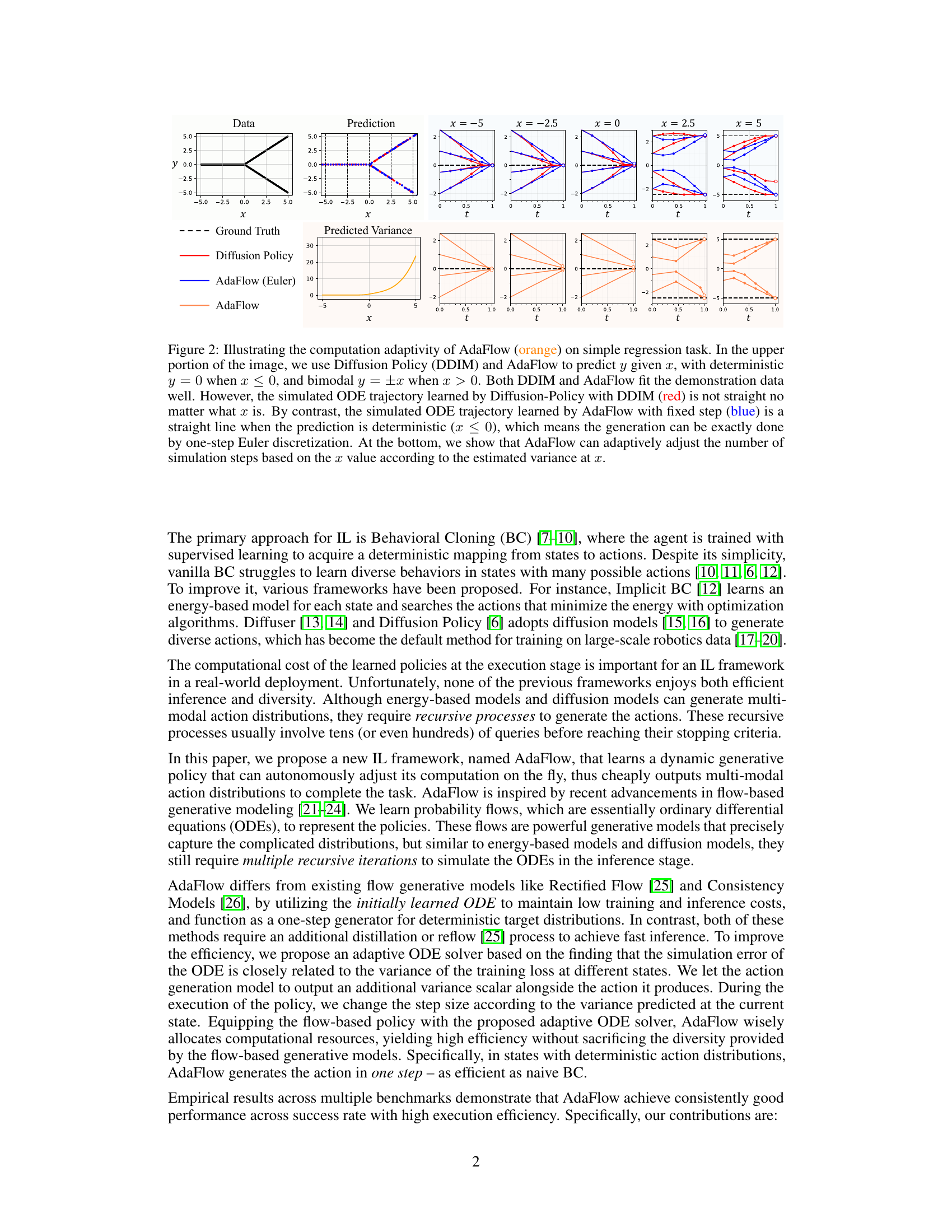
This figure compares the performance of AdaFlow and Diffusion Policy. It shows that AdaFlow can generate actions much faster than Diffusion Policy, especially in low-variance states where it only requires a single step. In high-variance states, AdaFlow still significantly outperforms Diffusion Policy by requiring fewer simulation steps. The color bar visually represents the state variance, illustrating how the algorithm adapts the number of steps to the variance of the state. This adaptive strategy allows AdaFlow to maintain high speed across different states.

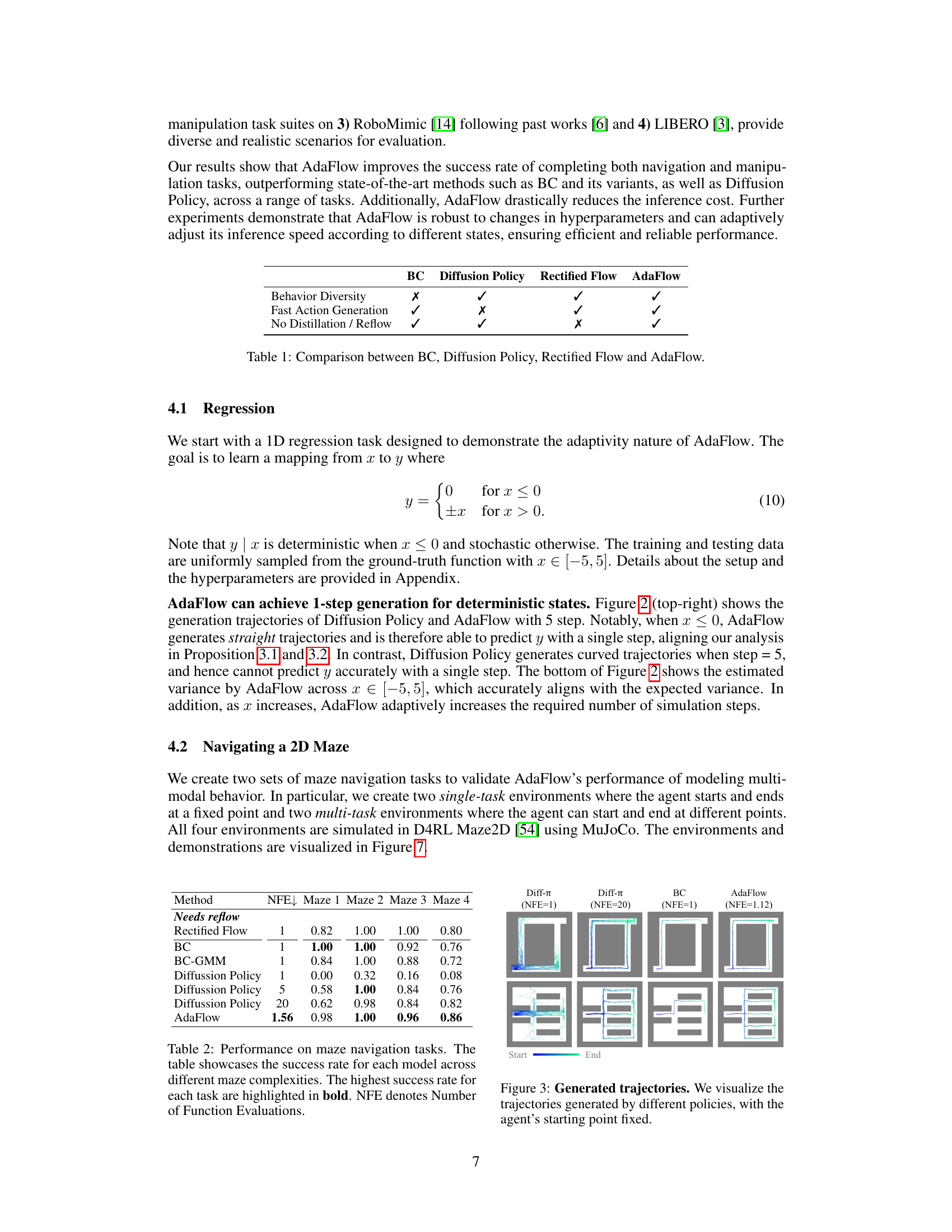
This table compares four different imitation learning methods: Behavior Cloning (BC), Diffusion Policy, Rectified Flow, and AdaFlow. It highlights their capabilities in generating diverse behaviors, achieving fast action generation, and avoiding the need for distillation or reflow techniques. Each method is marked with a checkmark (✓) or cross (✗) to indicate the presence or absence of each capability. BC is shown to be fast but not diverse, while the others offer diversity but at the cost of slower inference, except for AdaFlow, which aims to combine both speed and diversity.

In-depth insights

#

AdaFlow Overview

#

AdaFlow is presented as a novel imitation learning framework that addresses the limitations of diffusion-based methods by employing flow-based generative modeling. Its core innovation lies in a variance-adaptive ODE solver that dynamically adjusts the number of simulation steps during inference. This adaptive mechanism significantly speeds up inference without sacrificing the diversity of generated actions, achieving performance comparable to diffusion models but with drastically reduced computational cost. The framework cleverly links the conditional variance of the training loss to the discretization error of the ODEs. This insight allows AdaFlow to function as a near one-step generator for deterministic actions, while intelligently increasing the number of steps for more complex, multi-modal distributions. The paper highlights empirical evidence showcasing AdaFlow’s superior performance across various benchmarks, demonstrating improvements in success rates with significantly faster inference times than competing state-of-the-art methods. A key strength lies in its theoretical analysis, which supports the design choices and provides an error bound for the adaptive solver. Overall, AdaFlow provides a compelling alternative for efficient and diverse action generation in imitation learning.

Variance Adaptation

#

The concept of variance adaptation in the context of this research paper revolves around dynamically adjusting the model’s behavior based on the uncertainty of the predicted action. The core idea is that when the model is highly confident (low variance), a single, fast prediction step suffices. Conversely, in situations of high uncertainty (high variance), a more extensive, multi-step process is necessary to ensure accuracy. This adaptive mechanism is crucial for improving computational efficiency without compromising the quality of the generated actions. By directly connecting the variance of the training loss to the discretization error of the underlying ODE, the algorithm effectively becomes a self-regulating system, choosing the most efficient sampling strategy according to the inherent complexity of the state. This is particularly valuable in applications such as robotics and decision-making, where both speed and precision are essential. Adaptivity, therefore, is the key to balancing computational cost and performance.

Empirical Results

#

The empirical results section of a research paper is crucial for validating the claims made. A strong empirical results section will present data that is clearly presented and easy to interpret, using appropriate visualizations and statistical methods. It should compare the proposed method’s performance to relevant baselines, demonstrating that the proposed approach yields significant improvements in key metrics. The discussion of the results must be comprehensive, addressing both the strengths and limitations of the findings. Robustness analysis, showing how performance varies under different conditions or with changes in hyperparameters, is vital. Ideally, the section also includes an ablation study to isolate the effect of individual components of the method, demonstrating the contribution of each part. Finally, a strong section will connect the empirical findings back to the paper’s overall contributions and place the results within the broader context of the research field.

Limitations & Future

#

The study’s limitations center on the reliance on offline data, potentially limiting the generalizability of the model to unseen scenarios. Further, the variance estimation network’s accuracy impacts the adaptive ODE solver’s effectiveness, suggesting potential improvements in this area could enhance performance. Computational demands for training and inference, while reduced compared to some alternatives, remain a consideration, especially for complex real-world tasks. Future research directions include exploring online learning methods to enhance model adaptability and investigating methods to improve robustness to noisy or incomplete data. Extending AdaFlow to handle continuous action spaces and incorporating more sophisticated ODE solvers could also enhance performance. Finally, further investigation into theoretical guarantees and error bounds could yield stronger analytical results and greater confidence in the model’s behavior.

Related Works

#

The ‘Related Works’ section of a research paper on AdaFlow, a novel imitation learning framework, would critically analyze existing approaches to imitation learning and generative modeling. It would likely highlight diffusion-based methods like Diffuser and Diffusion Policy, emphasizing their strengths in generating diverse actions but acknowledging their computational limitations due to recursive processes. The discussion would then contrast these with flow-based generative models, such as Rectified Flow and Consistency Models, focusing on their efficiency but noting the challenges in ensuring multi-modal action generation. A key element would be a comparison of AdaFlow’s approach to these existing methods, highlighting AdaFlow’s variance-adaptive ODE solver as the unique contribution that enables efficient inference without sacrificing diversity. This section is crucial for establishing AdaFlow’s novelty and significance within the current state-of-the-art, clearly defining its position relative to previously established techniques.

More visual insights

#

More on figures

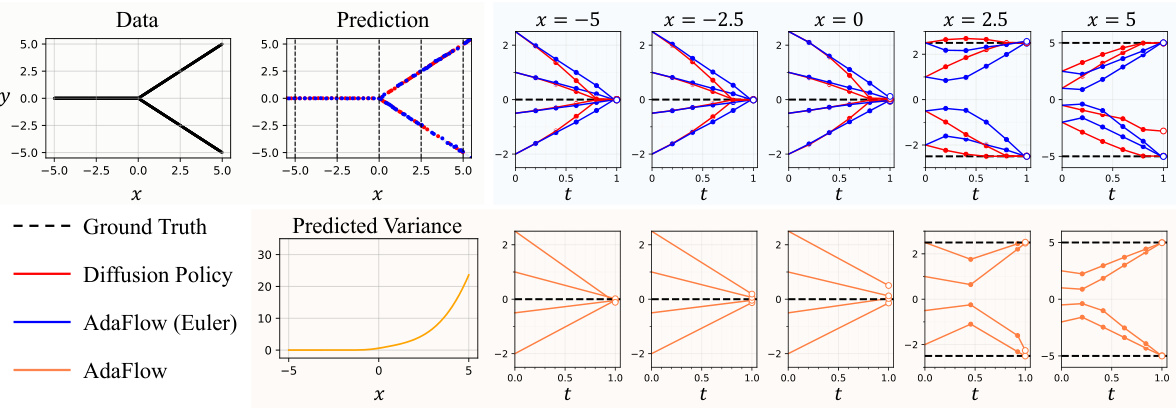
This figure demonstrates AdaFlow’s adaptive computation. The top shows the prediction of y from x using AdaFlow and Diffusion Policy. AdaFlow generates a straight line when the prediction is deterministic, demonstrating its one-step generation capability. The bottom shows how AdaFlow adjusts the number of simulation steps based on the variance at x, achieving efficiency while maintaining accuracy.

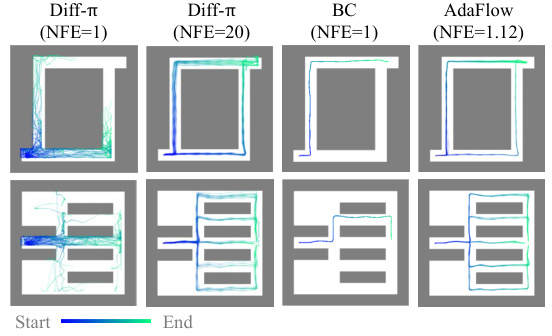
This figure compares the trajectories generated by four different methods: Diffusion Policy with 1 and 20 function evaluations, behavioral cloning, and AdaFlow. It shows that AdaFlow generates trajectories that are both diverse and efficient, while Diffusion Policy with only 1 function evaluation is less successful and less diverse in its results. Behavioral cloning’s trajectories are relatively constrained.

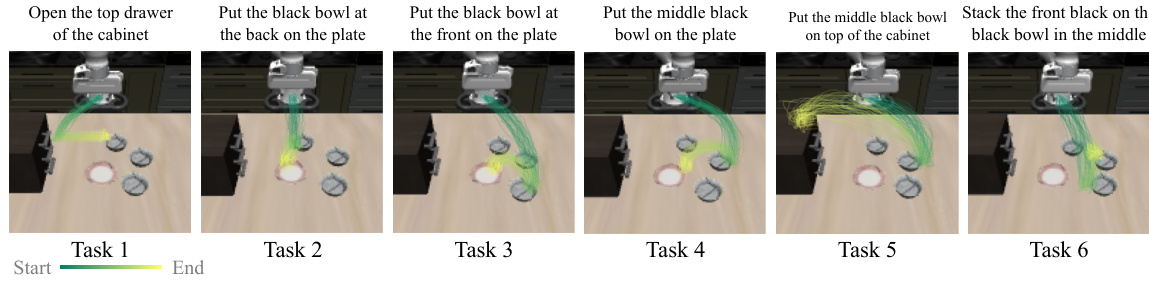
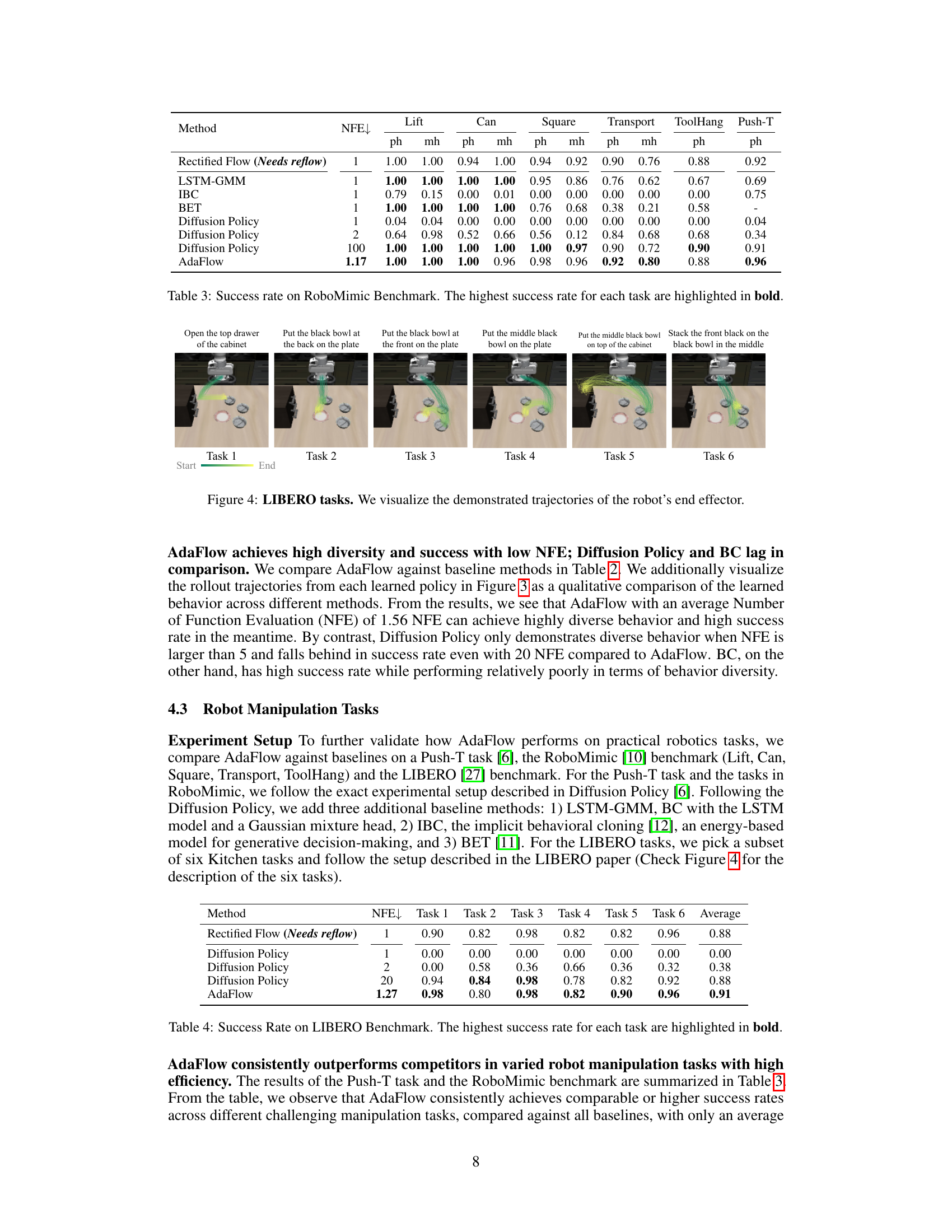
This figure shows six different manipulation tasks from the LIBERO benchmark dataset. Each subfigure shows a single task, visualizing the robot’s end effector movements. The trajectories illustrate the complexity and diversity of the actions involved, highlighting the challenges in robotic manipulation and the ability of the model to execute them effectively.

This figure compares the ground truth variance with the variance predicted by AdaFlow across different states during robot manipulation tasks. The top row shows the ground truth variance, visualized as a colormap on the robot arm’s trajectory during a series of actions. The bottom row displays AdaFlow’s variance prediction for the same task, using similar color coding. It demonstrates AdaFlow’s ability to accurately estimate the variance in states with complex action distributions (high variance), while maintaining efficiency in states with more straightforward deterministic actions (low variance).

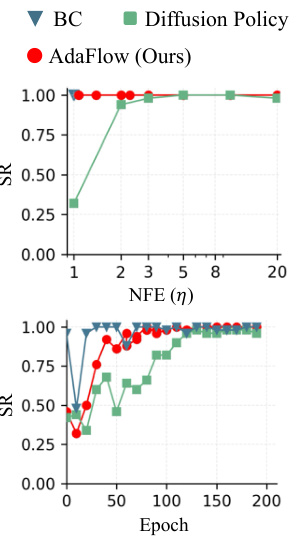
This figure presents ablation studies on AdaFlow, comparing its performance with baselines (BC and Diffusion Policy) across different metrics. The top panel shows success rate (SR) against the number of function evaluations (NFE), demonstrating AdaFlow’s efficiency in achieving high success rates even with low NFE. The bottom panel illustrates the training efficiency by displaying success rate over epochs, highlighting AdaFlow’s faster learning speed compared to Diffusion Policy.

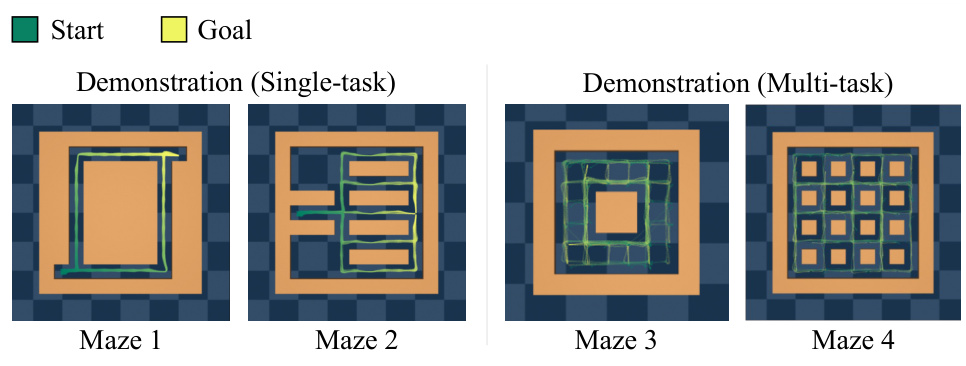
This figure visualizes 100 demonstration trajectories for four different mazes. Two mazes are single-task, meaning the agent always starts and ends in the same location, and two mazes are multi-task, where the start and end locations vary. The trajectories show the paths taken by an expert agent to navigate these mazes, illustrating the diverse and complex behaviors involved in maze navigation. These demonstrations were used to train the AdaFlow model. The color intensity represents the speed of the agent, with brighter colors denoting higher speed.

This figure visualizes 100 demonstration trajectories for four different maze environments (Maze1, Maze2, Maze3, Maze4). Each maze presents a unique navigational challenge with varying complexity and layout. The trajectories showcase the diverse paths taken by an expert agent to navigate each maze, highlighting the multi-modality and complexity of the task that an imitation learning algorithm needs to capture.

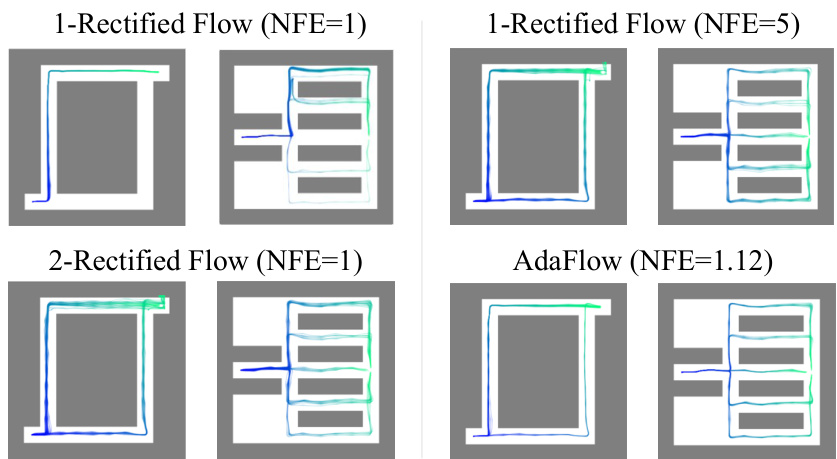
This figure compares the trajectories generated by standard Rectified Flow and AdaFlow in a maze navigation task. The visualization highlights the difference in path planning and action generation between the two methods. Standard Rectified Flow, even with multiple steps (NFE=5), struggles to produce diverse and efficient paths. In contrast, AdaFlow efficiently generates diverse and effective trajectories with a significantly lower number of function evaluations (NFE=1.12). The figure underscores AdaFlow’s improved efficiency and ability to produce diverse and effective behaviors.

More on tables

This table presents the performance of different models on four maze navigation tasks with varying complexities. The success rate (percentage of times the task was successfully completed) is shown for each model, along with the average number of function evaluations (NFEs) required for each task completion. The best performance for each maze is highlighted in bold. This helps compare the efficiency and effectiveness of different methods in navigating mazes.

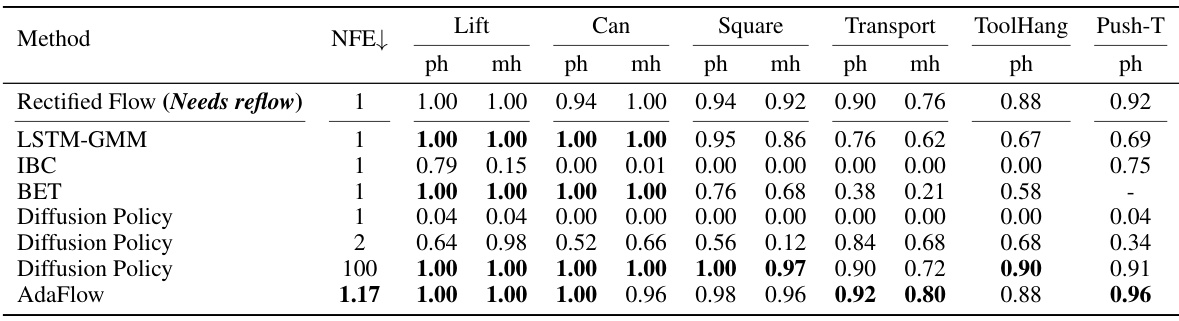
This table presents a comparison of the success rates achieved by different methods on the RoboMimic benchmark. The benchmark consists of several robot manipulation tasks. Each row represents a different method (Rectified Flow, LSTM-GMM, IBC, BET, Diffusion Policy at different numbers of function evaluations (NFEs), and AdaFlow). The columns represent the success rate for each task (Lift, Can, Square, Transport, ToolHang, Push-T) and the average number of function evaluations (NFE) required. The highest success rate for each task is highlighted in bold.

This table presents the success rates of different methods on the LIBERO benchmark, a set of robot manipulation tasks. The methods compared include Rectified Flow (requiring a reflow step), Diffusion Policy (tested with different numbers of function evaluations (NFE)), and AdaFlow. The table highlights AdaFlow’s consistently high success rates, particularly notable given its low average NFE of 1.27, demonstrating high efficiency.

This table presents the results of an ablation study conducted to evaluate the impact of the variance estimation network on the performance of AdaFlow. It compares the success rates of AdaFlow with and without the variance estimation network across four different maze navigation tasks (Maze1, Maze2, Maze3, Maze4). The results demonstrate that incorporating the variance estimation network significantly improves AdaFlow’s performance.

This table compares the performance of AdaFlow trained using two different methods: separate training and joint training. The results show success rates across four different maze tasks (Maze1-Maze4). Separate training is faster but the performance difference between the two methods is minimal.

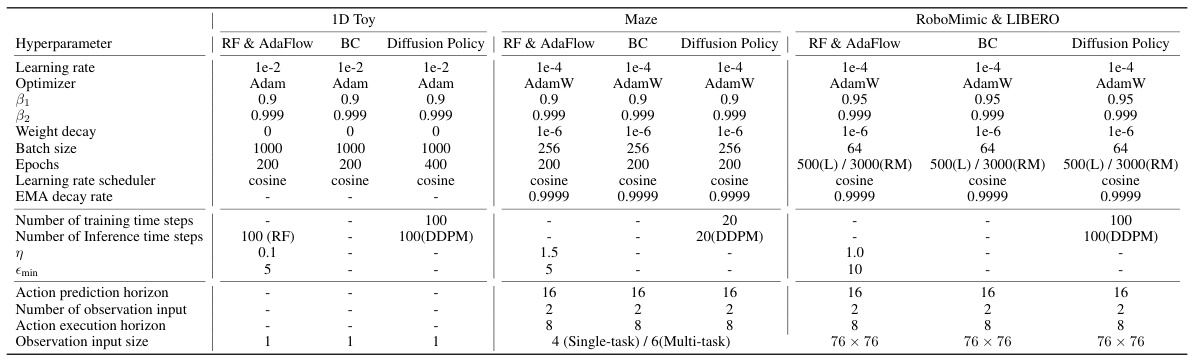
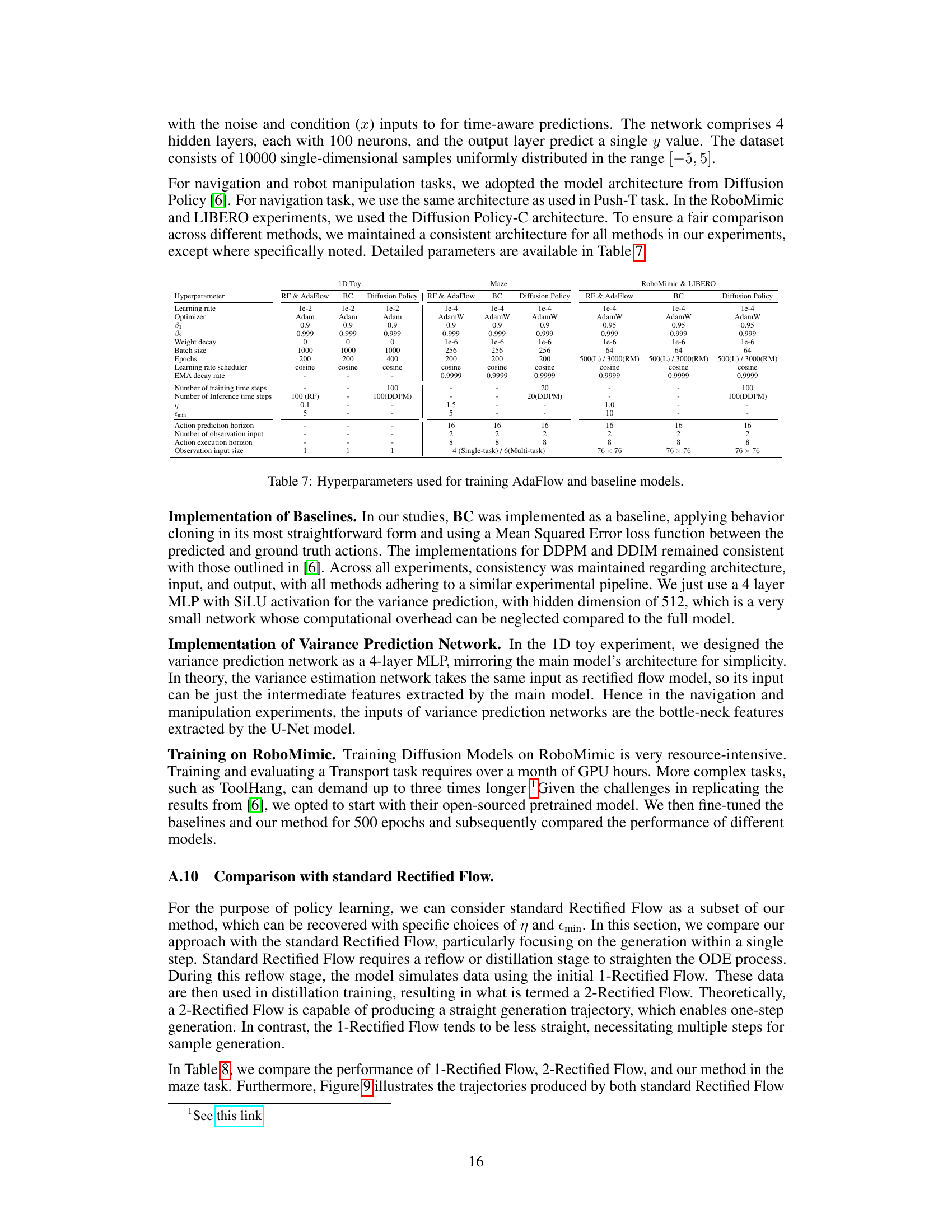
This table lists the hyperparameters used for training AdaFlow and three baseline models (BC, Diffusion Policy, and Rectified Flow) across three different task types: 1D toy regression, 2D maze navigation, and robot manipulation tasks (RoboMimic & LIBERO). For each model and task, the table specifies the learning rate, optimizer, beta1 and beta2 values for the optimizer, weight decay, batch size, number of epochs trained, learning rate scheduler, exponential moving average (EMA) decay rate, the number of training and inference steps, the error threshold (η), the minimum step size (ϵmin), action prediction horizon, number of observation inputs, action execution horizon, and the size of the observation input.

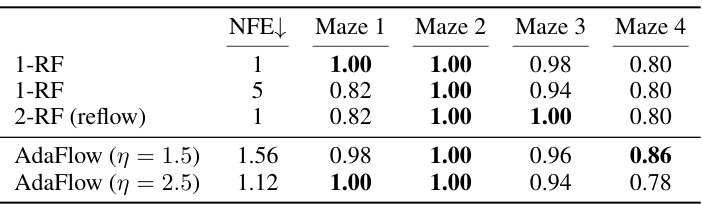
This table compares the performance of several models, including AdaFlow, on four different maze navigation tasks. The success rate (SR) is shown for each model and each maze, highlighting the best performance for each task. It demonstrates that AdaFlow achieves competitive performance with low computational cost. The table also points out that the 2-Rectified Flow model requires an expensive distillation training stage, which contrasts with AdaFlow’s efficiency.

Full paper

#