↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
In-context learning (ICL) is the ability of pretrained models to perform tasks based only on a few examples in the prompt without further training. While previous research focused on linear functions, this paper tackles the more challenging scenario of nonlinear functions, particularly in high-dimensional spaces. Existing methods often struggle with the sample complexity, requiring a number of examples that scales with the input dimension. This poses a significant challenge as practical applications frequently involve high-dimensional data.
The paper proposes a novel method using pretrained transformers with a nonlinear MLP layer to improve ICL efficiency. They focus on single-index models, a type of nonlinear function, where only a single linear combination of inputs influences the output. Through rigorous theoretical analysis, they show that the in-context sample complexity scales with the intrinsic dimensionality of the function, rather than the input dimensionality. This suggests that transformers are inherently adept at identifying and exploiting low-dimensional structure within high-dimensional datasets, thus achieving sample efficiency. The method outperforms baseline algorithms in both theoretical and empirical settings.
Key Takeaways#
Why does it matter?#
This paper is crucial because it demonstrates the surprising efficiency of pretrained transformers in learning complex, nonlinear functions from limited in-context examples. It challenges existing assumptions about ICL and opens new avenues for research into the adaptive capabilities of neural networks, particularly in applications dealing with high-dimensional data.
Visual Insights#

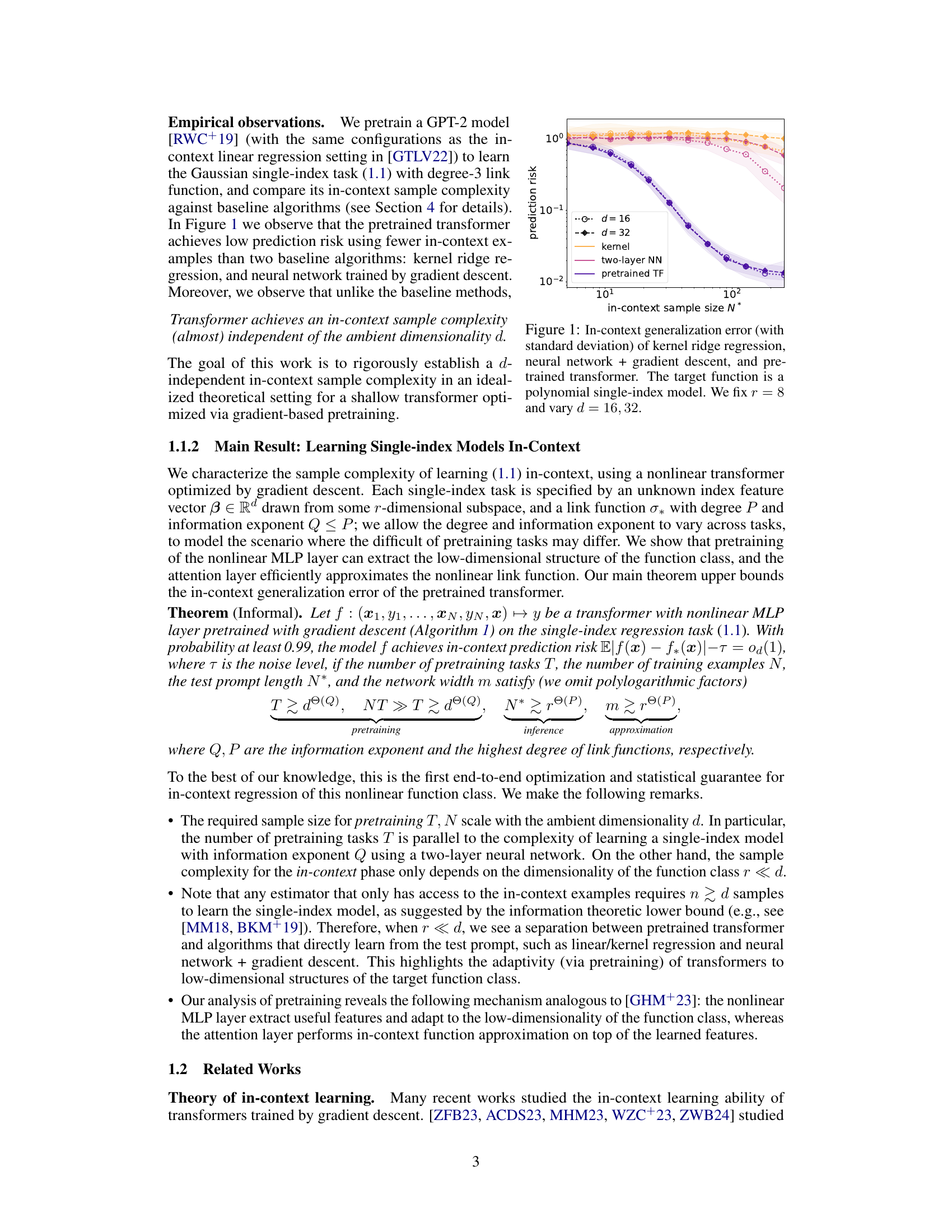
The figure shows the in-context generalization error for three different learning algorithms: kernel ridge regression, a two-layer neural network trained with gradient descent, and a pretrained transformer. The task was to learn a polynomial single-index model, where the dimensionality of the index feature vector (r) was fixed at 8 while the ambient dimensionality (d) was varied (16 and 32). The plot illustrates the prediction risk as a function of the number of in-context examples (N*). It demonstrates that the pretrained transformer achieves lower prediction risk with fewer in-context examples compared to the baseline algorithms.
In-depth insights#
ICL’s Efficiency#
In-context learning (ICL) presents a compelling paradigm shift in machine learning, yet its efficiency remains a subject of significant debate. Existing analyses often focus on linear models, failing to capture the full scope of ICL’s capabilities with nonlinear functions. This paper delves into the efficiency of ICL for low-dimensional nonlinear function classes. By leveraging pretrained transformers, the model demonstrates remarkable sample efficiency, outperforming baseline algorithms that only access the test prompt. This efficiency stems from the transformer’s ability to adapt to low-dimensional structures inherent in the target function class, effectively extracting underlying patterns from the training data. The key insight is that the pretraining process allows the model to identify and learn these structural aspects, leading to improved generalization and reduced sample complexity during the in-context phase. Future research should explore this adaptivity further and determine how these findings translate to high-dimensional settings and more complex tasks, potentially unlocking new frontiers in sample-efficient learning.
Nonlinear ICL#
Nonlinear in-context learning (ICL) presents a significant challenge and opportunity in the field of machine learning. Linear ICL, where models learn linear functions from examples, has been extensively studied, but real-world problems often involve nonlinear relationships. Understanding how pretrained transformers, known for their ICL capabilities, handle nonlinearity is crucial. This involves investigating how the model’s architecture, particularly attention mechanisms and multilayer perceptrons (MLPs), interact with nonlinear activation functions to implicitly learn complex mappings. Key questions include the capacity of transformers to approximate various nonlinear function classes, how the complexity scales with the data dimensionality, and the impact of pretraining data on generalization performance. Analyzing the optimization landscape associated with nonlinear ICL is particularly important to understand convergence and sample efficiency, as non-convexity introduces unique challenges. Theoretical frameworks that establish sample complexity bounds and performance guarantees for specific classes of nonlinear functions are needed to better guide the design and deployment of such models. Ultimately, a deep understanding of nonlinear ICL is key to advancing the capabilities and reliability of in-context learning for broader applications.
Transformer Adaptivity#
The concept of “Transformer Adaptivity” in the context of in-context learning (ICL) centers on the pretrained transformer’s ability to efficiently learn diverse function classes without explicit parameter updates. This adaptivity is not merely about fitting functions, but also about generalizing effectively to unseen data and leveraging inherent structures within the function class. The paper explores this adaptivity by studying a nonlinear function class (Gaussian single-index models) which requires the transformer to adapt not only to the nonlinearity but also to the low-dimensional distribution of target functions. The analysis reveals that the pretrained transformer’s architecture, particularly the interplay between the MLP and attention layers, enables this efficient adaptivity by effectively identifying and leveraging these low-dimensional structures, leading to sample-efficient ICL that surpasses algorithms restricted to in-context data alone. The key is that pretraining enables an implicit learning algorithm, allowing the transformer to quickly adjust to the specific function presented in the prompt. This adaptability, a core strength of transformers, demonstrates their potential as highly effective few-shot learners.
Low-Dim Structures#
The concept of ‘Low-Dimensional Structures’ in machine learning signifies that despite high-dimensional input data, the underlying relationships or target functions often reside within a lower-dimensional subspace. This is a crucial observation because it suggests that the complexity of learning can be significantly reduced by identifying and exploiting this inherent structure. Pretrained transformers, with their ability to learn in-context, demonstrate a remarkable capacity to adapt to these low-dimensional structures. This is important because it allows them to outperform algorithms that operate directly on the raw high-dimensional data, achieving sample efficiency and superior generalization. The exploration of low-dimensional structures through techniques like single-index models helps unveil the true underlying complexity of machine learning problems. Understanding these structures is key to developing more efficient algorithms and better utilizing the power of pretrained models. This adaptive capability suggests that rather than explicitly searching the full high-dimensional space, the pretrained transformer learns to implicitly focus on the relevant lower-dimensional structure during the in-context learning phase. This sample efficiency inherent in identifying and leveraging these low-dimensional structures is a significant advantage.
Future ICL Research#
Future in-context learning (ICL) research should prioritize addressing the limitations of current models. Improving the sample efficiency of ICL, especially for high-dimensional data, is crucial. This involves investigating how model architecture and pretraining strategies can be optimized to adapt to low-dimensional structures within complex datasets. Furthermore, theoretical analysis needs to extend beyond linear settings, focusing on nonlinear function classes and complex input-output relations. Understanding the relationship between pretraining and in-context performance is key; future work should explore how diverse pretraining tasks can be optimally selected and combined to improve generalization. Finally, addressing the robustness and safety of ICL models is critical. Research should investigate potential biases, vulnerabilities to adversarial attacks, and mechanisms for ensuring reliable performance in real-world applications.
More visual insights#
More on figures
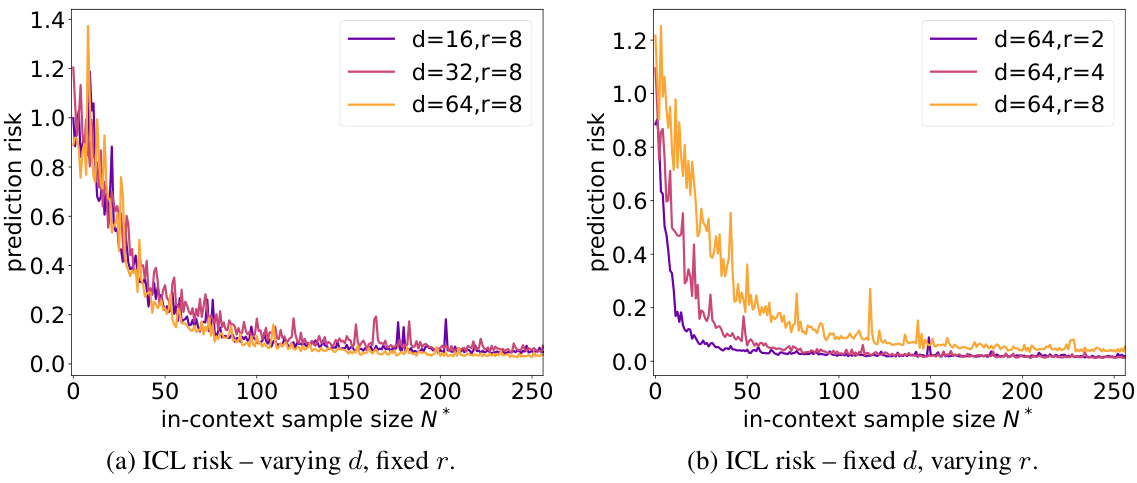
This figure displays the in-context sample complexity results for a GPT-2 model trained on Gaussian single-index functions with a degree-4 polynomial. The left subplot (a) demonstrates the model’s performance across varying ambient dimensions (d) while keeping the target subspace dimensionality (r) constant. The results show that the in-context sample complexity is nearly independent of the ambient dimension, suggesting adaptability to the underlying low-dimensional structure. The right subplot (b) shows the impact of varying the target subspace dimensionality (r) while keeping the ambient dimension (d) constant. As expected, increasing the target dimensionality increases the required number of in-context examples for effective learning.
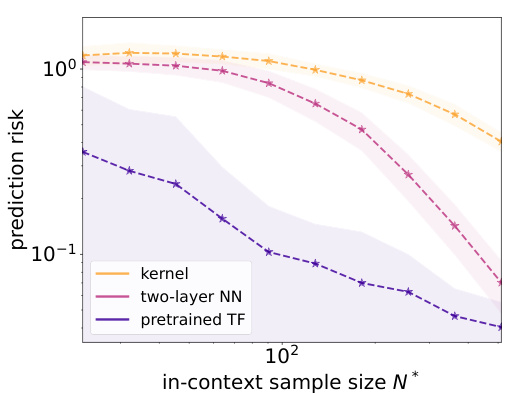
This figure compares the in-context generalization error for three different methods: kernel ridge regression, a two-layer neural network trained with gradient descent, and a pretrained transformer. The experiment uses a polynomial single-index model as the target function, keeping the subspace dimensionality (r) constant at 8 while varying the ambient dimensionality (d) between 16 and 32. The x-axis represents the number of in-context examples used, and the y-axis represents the prediction risk (generalization error). The shaded areas represent the standard deviations.
Full paper#