Parameter Symmetry and Noise Equilibrium of Stochastic Gradient Descent

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it bridges the gap between theoretical understanding and practical applications of SGD. It offers a new perspective on common deep learning phenomena and provides insights into representation formation and other optimization techniques, thus impacting algorithm design and neural network architecture.

Visual Insights

#

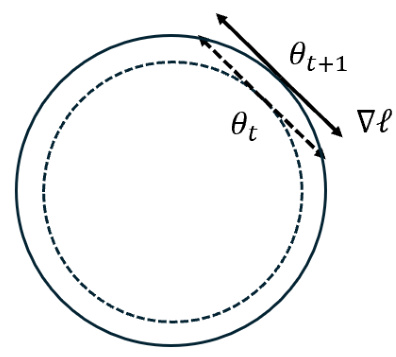
This figure illustrates the effect of scale invariance on the dynamics of SGD. In a deterministic setting (gradient flow), the parameters stay on the same circle, as the gradient is tangential. However, with SGD (stochastic), the noise causes the parameter vector to move outwards to larger circles, diverging to infinity. This illustrates that even with a small amount of noise, the dynamics of SGD can be qualitatively different from gradient flow.

In-depth insights

#

SGD Noise Dynamics

#

Analyzing SGD noise dynamics reveals crucial insights into deep learning. Stochasticity, introduced by mini-batching in SGD, isn’t merely random noise; it systematically biases the learning process. This bias, rather than hindering convergence, can be harnessed to understand phenomena like progressive sharpening/flattening and representation formation. The paper’s focus on continuous symmetries and their interplay with noise is particularly insightful. Noise equilibria, where noise contributions from different directions balance, are identified as unique attractors. This framework elegantly unifies diverse phenomena and offers a mechanistic explanation for regularization effects observed in practice. However, a crucial limitation is the assumption of continuous-time dynamics. The effect of discrete time steps, which is central to practical SGD implementations, needs further investigation. Finally, the analysis of deep linear networks provides a concrete validation of the theory’s power, showcasing its capacity to explain observed behaviors beyond simplistic models.

Symmetry’s Role

#

The concept of symmetry plays a crucial role in understanding the dynamics of stochastic gradient descent (SGD) in deep learning. Symmetries, especially exponential symmetries, which encompass rescaling and scaling symmetries prevalent in deep learning architectures, fundamentally shape SGD’s trajectory. The paper demonstrates that the presence of symmetry leads to a systematic motion of parameters, a “Noether flow,” toward a unique, initialization-independent fixed point. This point, termed a noise equilibrium, signifies a balance and alignment of noise contributions from different directions. Therefore, symmetry is not just a structural property but a dynamic factor influencing SGD’s convergence behavior. The implications are far-reaching, providing a novel way to explain progressive sharpening/flattening and representation formation within neural networks and offering valuable insights into regularization techniques.

Noise Equilibria

#

The concept of “Noise Equilibria” in the context of stochastic gradient descent (SGD) is a novel theoretical framework that explains how noise inherent in SGD interacts with symmetries in loss functions. It proposes that, under certain conditions (primarily the presence of exponential symmetries), the noise contributions from different directions of the parameter space balance out, leading to unique, initialization-independent fixed points. These points are termed “noise equilibria” because the noise-induced dynamics effectively settle there. This is in contrast to gradient descent (GD), which often converges to different solutions based on initialization. The presence of these fixed points provide a mechanism for understanding seemingly random phenomena in deep learning, such as progressive sharpening/flattening and representation formation. This theoretical framework unifies the treatment of various common symmetries, providing a general approach to understanding how noise impacts SGD’s behavior. This offers valuable insights into the implications of representation normalization and other training techniques.

Deep Learning Implications

#

The study of parameter symmetry and noise equilibrium in stochastic gradient descent (SGD) offers profound implications for deep learning. Understanding how symmetries interact with the inherent noise in SGD reveals novel mechanisms for phenomena like progressive sharpening and flattening of loss landscapes, which are crucial for model generalization. The concept of ’noise equilibria,’ where noise contributions are balanced, provides a new lens through which to analyze the dynamics of SGD, explaining why it often outperforms gradient descent in practice. This framework also potentially offers new insights into regularization techniques like representation normalization and warmup, connecting the role of noise and symmetry in mitigating overfitting and ensuring stable training. Furthermore, the research highlights the systematic bias introduced by noise in the degenerate directions of loss functions, leading to a deeper understanding of representation formation within neural networks. These results provide theoretical foundations for the often-observed empirical success of SGD, paving the way for the development of novel training algorithms and improved optimization strategies.

Future Directions

#

Future research could explore extending the theoretical framework beyond exponential symmetries to encompass a broader range of symmetries prevalent in deep learning models. Investigating the interplay between noise equilibrium and other deep learning phenomena, such as generalization and optimization landscapes, warrants further attention. Empirically validating the theoretical findings on a wider variety of architectures and datasets is crucial, as is exploring the practical implications of noise equilibrium for hyperparameter tuning and algorithm design. A deeper understanding of how noise equilibrium interacts with different activation functions and regularization techniques would also be beneficial. Finally, exploring the connections between noise equilibrium and the implicit biases of SGD, particularly in the context of representation learning and generalization, represents an exciting avenue for future research.

More visual insights

#

More on figures

This figure compares the performance of gradient descent (GD) and stochastic gradient descent (SGD) in matrix factorization. The left panel shows a learning trajectory, illustrating that SGD converges exponentially fast. The middle panel tracks 10 individual elements of the matrix difference (UTUU - WWW), demonstrating that they converge to zero under SGD, fluctuating minimally around zero. The right panel highlights that the final solutions obtained by SGD, despite agreeing with the theoretical predictions, significantly differ from GD solutions (by an order of magnitude), irrespective of the initial parameters.

This figure compares the results of training a two-layer linear network with SGD and GD, with and without weight decay, for different data covariances. The left panel shows that SGD leads to norm-balanced solutions only when the data covariance is isotropic (φx = 1), while GD always converges to norm-balanced solutions. The right panel shows that SGD’s solutions exhibit progressive sharpening or flattening depending on the data distribution, unlike GD. The difference is explained by the noise equilibrium of SGD.

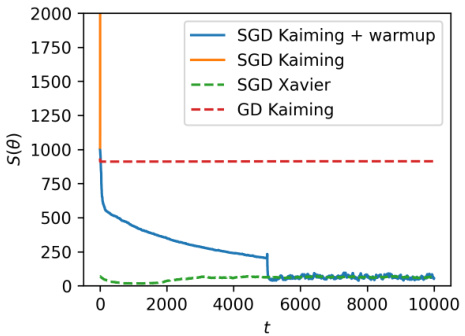
This figure shows the dynamics of the stability condition S (trace of Hessian) during the training process of a rank-1 matrix factorization problem. It compares the performance of SGD with Kaiming initialization (with and without warmup), SGD with Xavier initialization, and GD with Kaiming initialization. The results demonstrate that with a proper learning rate scheduling (warmup), SGD with Kaiming init. improves the stability condition, while other methods do not improve or even worsen the stability during training. The unique equilibrium under SGD is also illustrated.

This figure compares the evolution of parameter norms in two different neural networks (Net A and Net B) trained using SGD and GD. Both networks exhibit scaling symmetry, meaning their loss remains unchanged when all parameters are scaled by a constant factor. The figure demonstrates that, under SGD, the total norm of parameters and individual layer norms monotonically increase, even when layer-wise symmetry is absent. In contrast, GD training maintains a constant parameter norm in Net B, which possesses both global and layer-wise scaling symmetries.

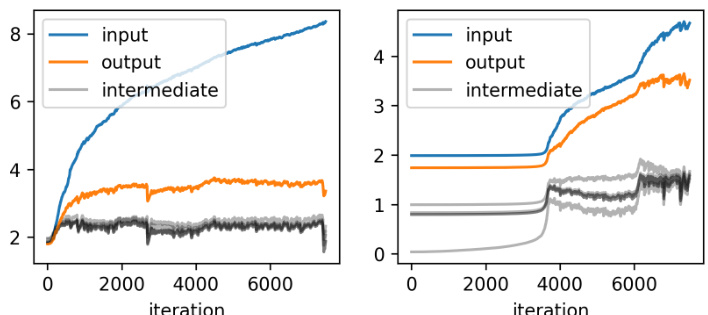
This figure compares the learned latent representations of a two-layer tanh network trained using SGD and GD. The left panels show that the latent representations learned with SGD are similar across layers, consistent with the paper’s theory. The right panels demonstrate that GD produces dissimilar representations across layers. The plots visualize the matrices WΣW (covariance of pre-activations in the first layer) and UΣU. This highlights a key difference in the feature learning of SGD vs. GD.

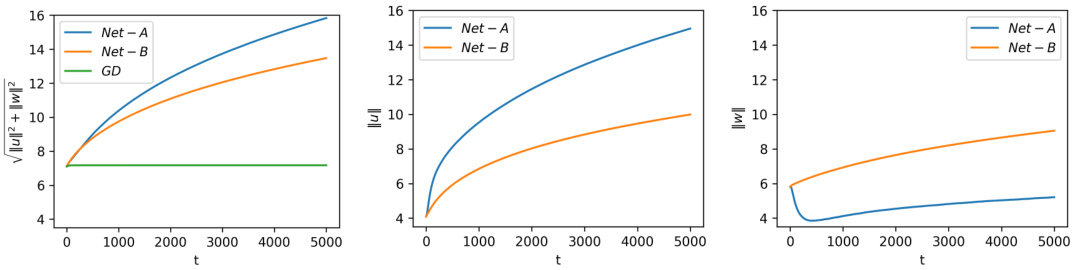
The figure shows the evolution of the norm of parameters in two different neural networks (Net-A and Net-B) trained using SGD and GD. Net-B has layer-wise rescaling symmetry, causing its parameter norms to always increase monotonically under SGD but remain constant under GD. Net-A lacks this layer-wise symmetry, resulting in varying norms in each layer under SGD.

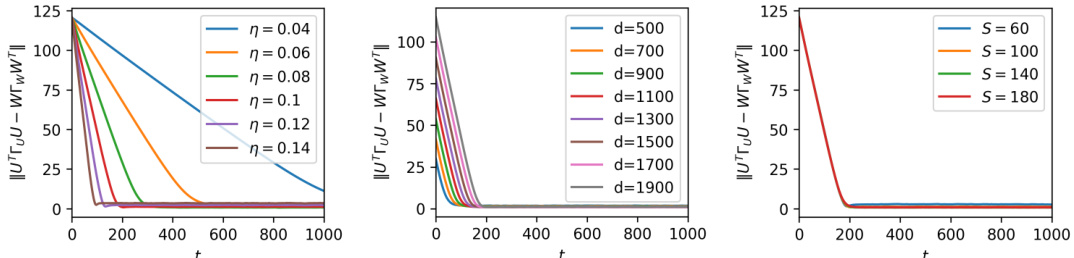
The figure shows how the convergence speed to the noise equilibria is affected by different hyperparameters such as learning rate, data dimension, and batch size. The robustness of the convergence to the equilibria against these variations is demonstrated.

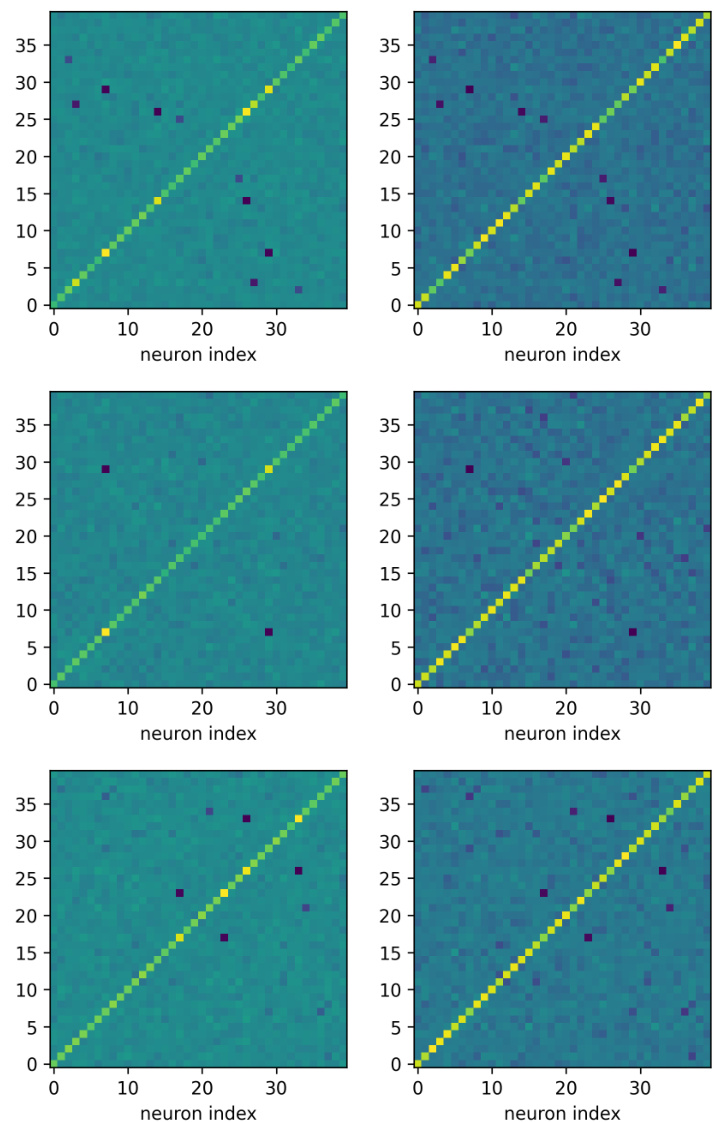
This figure compares the latent representations learned by SGD and GD for a two-layer tanh network. The left side shows that SGD produces similar representations across different layers, aligning with the paper’s theory. The right side demonstrates that GD produces vastly different representations. The matrices shown (WEW and U’U) highlight the covariance of preactivation representations, demonstrating a qualitative difference in feature learning between the two optimization algorithms.

Full paper

#