↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Current methods for enhancing LLMs’ mathematical reasoning capabilities are expensive, either requiring large-scale data collection for pre-training or relying on powerful LLMs for problem synthesis. This leads to high costs and limits accessibility for researchers with limited resources.
This paper introduces JiuZhang3.0, which tackles this issue by training a small, efficient LLM to synthesize a large number of high-quality math problems. This approach significantly reduces the cost of data creation, making it a more accessible solution for researchers. The generated problems were then used to pre-train JiuZhang3.0, which demonstrates state-of-the-art performance on various mathematical reasoning benchmarks.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a cost-effective method for improving mathematical reasoning in large language models (LLMs). It challenges the conventional high-cost approaches by training a small LLM for data synthesis, significantly reducing training and inference expenses. This opens up new avenues for researchers with limited resources to contribute to the advancement of LLMs in mathematical reasoning and promotes broader accessibility in the field.
Visual Insights#

This figure compares the performance and cost of three different models: KPMath-DSMath-7B, Deepseek-Math-7B-RL, and JiuZhang3.0-7B. The left bar chart shows the accuracy of each model on three benchmark datasets (GSM8k, MATH, and ASDiv). The right bar chart shows the estimated total cost (in USD) for each model, highlighting the significantly lower cost of JiuZhang3.0-7B. This demonstrates that JiuZhang3.0-7B achieves state-of-the-art performance at a much lower cost than existing methods.
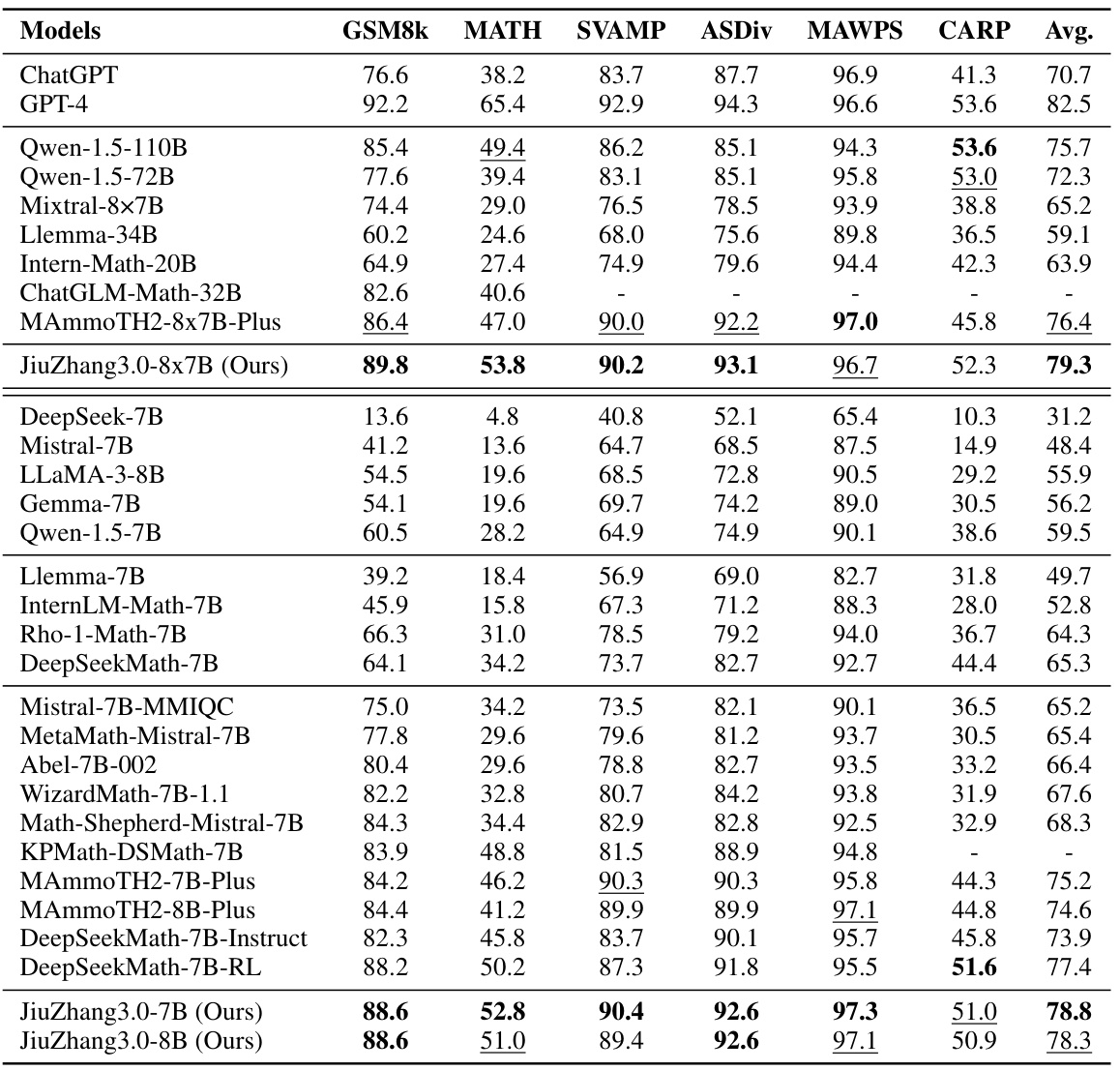
This table presents the performance of various large language models (LLMs) on six different datasets designed for natural language reasoning tasks. The models are categorized by size and type (e.g., open-source, fine-tuned). The table highlights the best and second-best performing models within similar size categories for each dataset, providing a comparison of performance across different LLMs.
In-depth insights#
Small Model Synthesis#
The concept of ‘Small Model Synthesis’ in the context of a research paper likely revolves around training relatively small language models (LLMs) to generate synthetic data, specifically for tasks like mathematical problem solving. This approach contrasts with methods that rely on large, computationally expensive models or extensive real-world data collection. The benefits include reduced costs and faster training times, making it more accessible to researchers with limited resources. However, a key challenge would be ensuring the quality and diversity of the synthetic data generated by a smaller model, to avoid negatively impacting the performance of downstream tasks. The success of this method hinges on clever techniques like knowledge distillation from larger models or careful prompt engineering, to maximize the smaller model’s effectiveness in data synthesis. The paper would likely present quantitative results comparing the performance of LLMs trained on small model-generated data against those trained on larger datasets or with different methods, demonstrating its efficiency and potential.
GPT-4 Knowledge Distillation#
The concept of “GPT-4 Knowledge Distillation” in the context of a research paper likely refers to a technique where a smaller, more efficient language model learns to mimic GPT-4’s capabilities, specifically in mathematical reasoning. This is achieved by training the smaller model on a dataset generated by GPT-4, effectively distilling GPT-4’s knowledge into a more resource-friendly model. This process usually involves crafting prompts to guide GPT-4 in generating high-quality training data that encompasses a wide range of mathematical problems and difficulty levels. The key advantage lies in reducing the computational cost and resource requirements associated with using large models like GPT-4 directly, making the technology more accessible and scalable. The effectiveness of the distillation process depends on several factors, including the quality and diversity of the GPT-4 generated dataset, the architecture of the smaller model, and the training methodology. A successful distillation would result in a model that performs comparably to GPT-4 on specific mathematical tasks but with significantly lower computational cost and resource needs. The technique represents a powerful strategy for democratizing access to advanced mathematical reasoning capabilities.
Gradient-Based Value Estimation#
Gradient-based value estimation is a crucial technique for efficiently selecting high-quality synthetic data in training machine learning models. It leverages the gradients of a reference model to quantify the influence of each synthetic data point on downstream tasks. By comparing gradient similarity between synthetic and real data, the method identifies valuable synthetic samples that significantly benefit downstream model performance. High-value data selection is achieved by prioritizing data with high gradient similarity, ensuring the efficient utilization of limited computational resources. This approach reduces the reliance on computationally expensive techniques, such as exhaustive evaluations, for data selection, making the process of data synthesis more cost effective. The method’s effectiveness depends on the choice of the reference model and the similarity metric used, offering flexibility and adaptability to various machine learning tasks and settings.
Multi-Source Data#
Utilizing multi-source data significantly enhances the robustness and generalizability of machine learning models. This approach leverages data from diverse sources, such as webpages, books, and research papers, to provide a more comprehensive representation of the knowledge domain. By combining multiple perspectives, we create a richer training dataset that reduces overfitting and improves the model’s ability to handle unseen data. The integration of these diverse sources allows for a more nuanced understanding of complex concepts. However, using multi-source data requires careful consideration of data cleaning, preprocessing, and potential biases across different data sources. Effective data harmonization is critical to ensure that the diverse data sources are properly aligned and integrated, allowing the model to learn effectively.
Cost-Effective Approach#
A cost-effective approach to enhancing mathematical reasoning in LLMs is presented, focusing on efficient data synthesis. Instead of relying on expensive large language models (LLMs) or massive datasets for pre-training, this method trains a smaller, more efficient LLM specifically for generating high-quality mathematical problems. This is achieved through knowledge distillation, transferring the data synthesis capabilities of a powerful LLM (like GPT-4) to the smaller model using a carefully curated dataset. The process is further optimized by employing gradient-based influence estimation to select the most valuable training data, reducing the number of GPT-4 API calls significantly. This strategy lowers the overall cost and computational resources needed, making it a more accessible and practical approach for improving the mathematical reasoning abilities of LLMs.
More visual insights#
More on figures

This figure illustrates the JiuZhang3.0 model training pipeline. It starts with a multi-source corpus of mathematical texts which are sampled and fed, along with prompts, into GPT-4 to create an initial knowledge distillation dataset. This dataset is used to train a small LLM for data synthesis. A gradient-based method selects the most valuable texts for a second, enhanced KD dataset, further improving the synthesis LLM. This enhanced LLM generates 4.6B synthetic data points that are filtered and used to pre-train the JiuZhang3.0 model in three sizes (7B, 8B, and 8x7B).

This figure shows how the performance of the JiuZhang3.0 model changes as the proportion of synthetic pre-training data increases. It compares the performance of JiuZhang3.0 trained on Mistral-7B and LLaMA-3-8B base models across three different mathematical reasoning datasets (GSM8k, MATH, and ASDiv). A dashed line represents the performance of the DeepSeekMath-7B model, a strong baseline model, for comparison. The results demonstrate that using a larger proportion of synthetic data improves the model’s performance, and that the LLaMA-3-8B base model shows better performance than the Mistral-7B base model.
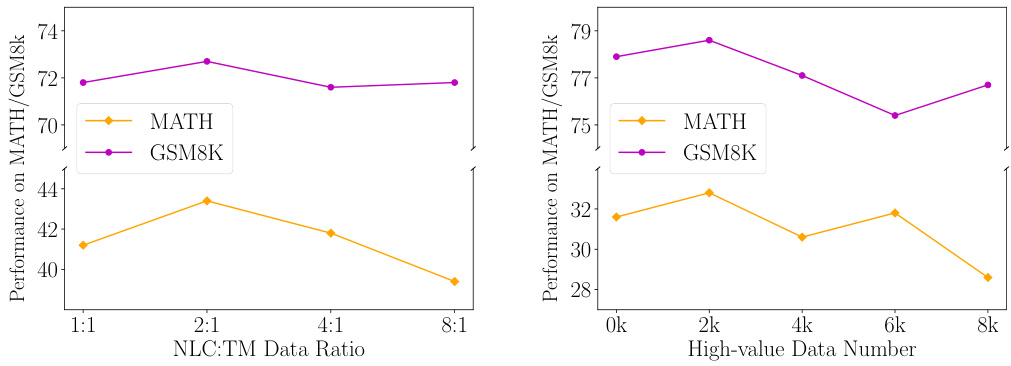
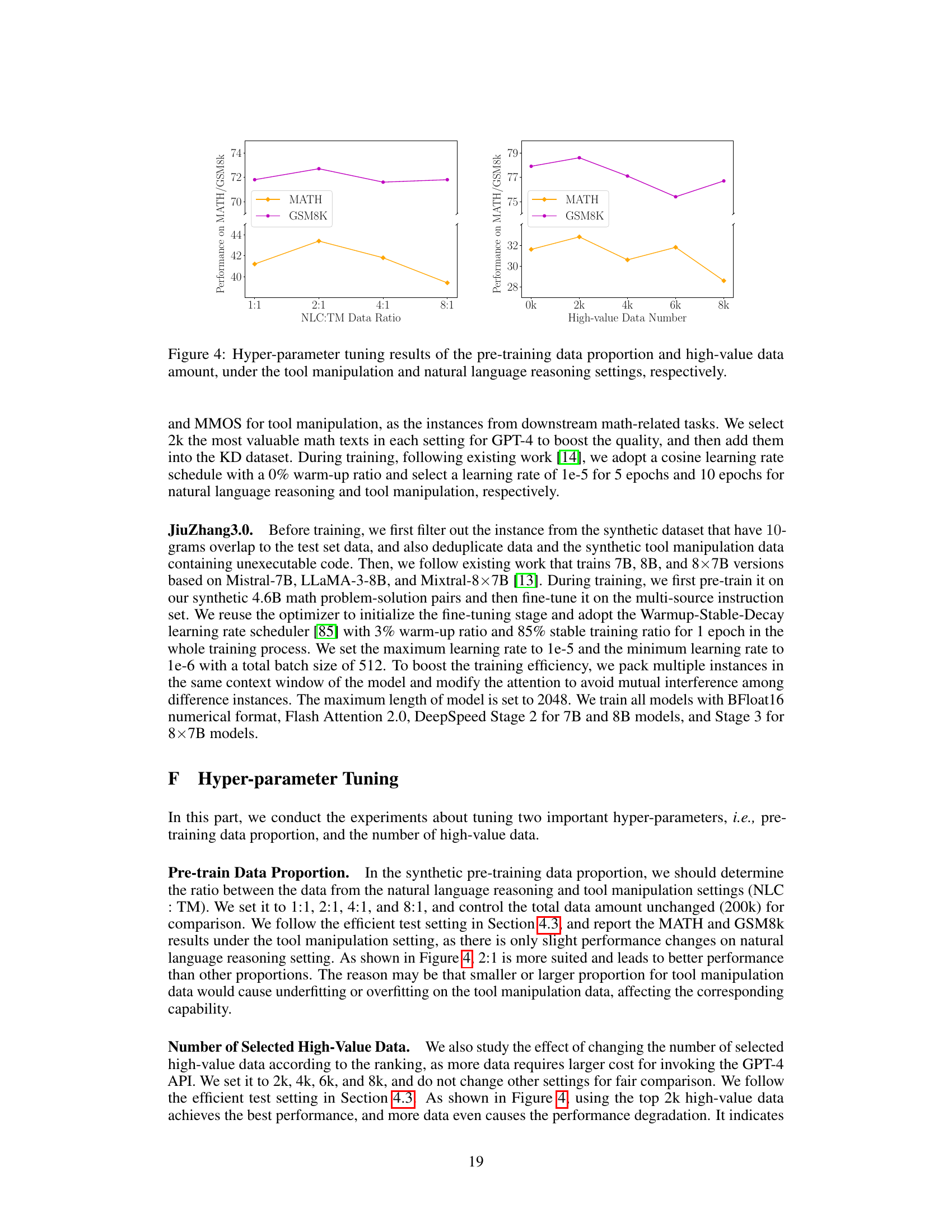
This figure displays the results of hyperparameter tuning experiments for the JiuZhang3.0 model. It shows how the model’s performance on MATH and GSM8k datasets changes with different ratios of natural language reasoning and tool manipulation data used for pre-training (left panel), and with varying amounts of high-value data included during training (right panel). The plots illustrate the impact of these hyperparameters on the model’s ability to perform mathematical reasoning tasks, helping to determine optimal settings for enhanced performance.

This figure illustrates the process of training the JiuZhang3.0 model. It starts with initializing a small LLM for math problem synthesis by knowledge distillation from GPT-4 using randomly sampled data. Then, it boosts this model’s performance by retraining it with high-value data selected using a gradient-based value estimation method. Finally, this improved model generates a large dataset of synthetic math problems used for pre-training the JiuZhang3.0 model.
More on tables

This table presents the performance of various LLMs on five benchmark datasets that differ in data format or domain. The datasets assess the models’ abilities in different aspects of reasoning and knowledge beyond purely mathematical ones, such as general knowledge and scientific understanding. The table highlights the best and second-best performing models within similar parameter scale groups, indicating the relative strengths of different architectures and training methodologies on these diverse tasks.
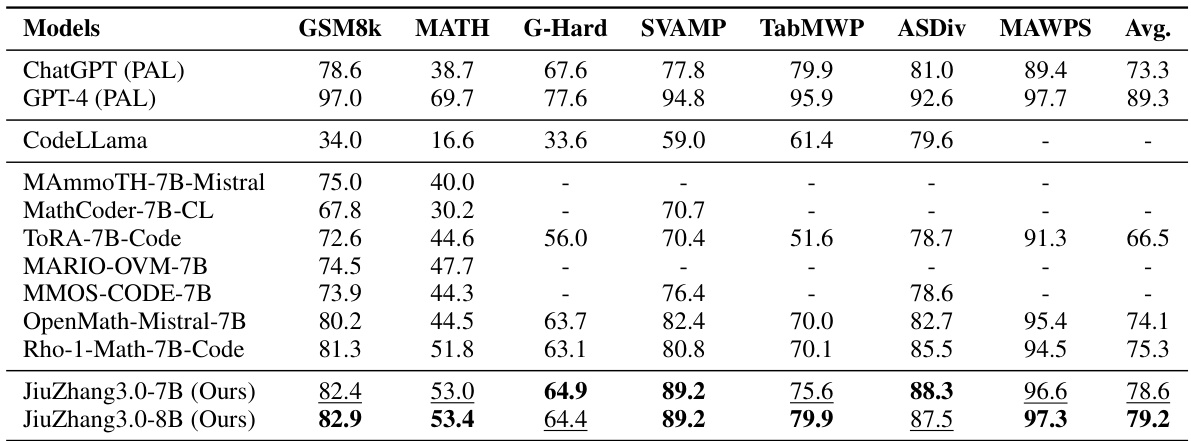
This table presents the performance of various LLMs on six mathematical reasoning datasets using a tool manipulation setting. The best and second-best performing models (among those with similar scales) are highlighted for each dataset, providing a comparison of different LLMs’ abilities to solve mathematical problems by using external tools.
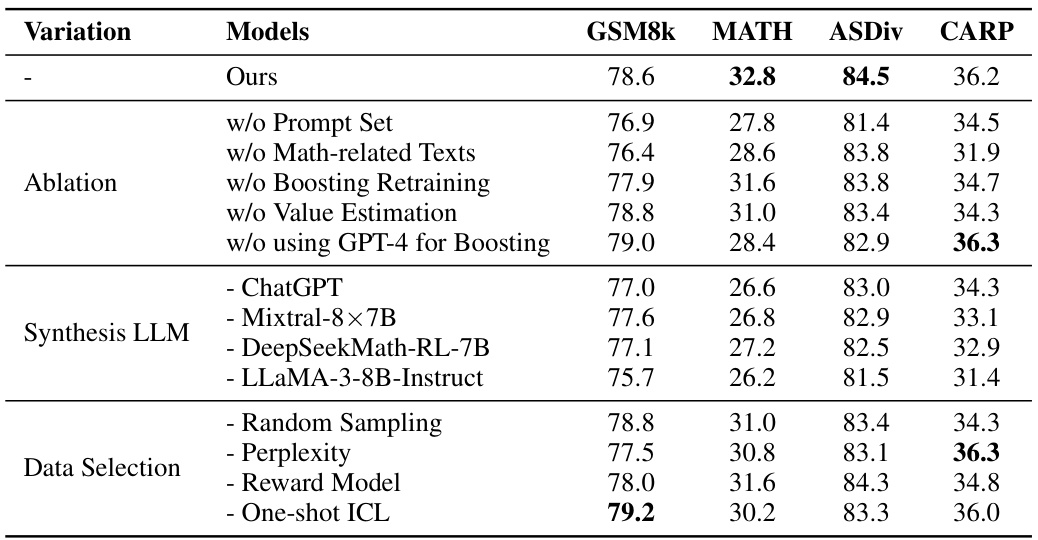
This table presents the results of several large language models (LLMs) on six different datasets designed for evaluating natural language reasoning capabilities, specifically focusing on mathematical problem-solving. The models are categorized by size, and their performance (accuracy) is shown for each dataset. The best and second-best performing models of similar sizes are highlighted for easier comparison.

This table presents the performance of various large language models (LLMs) on six different datasets designed for evaluating natural language reasoning capabilities, specifically focusing on mathematical problem-solving. The results show the accuracy of each model on each dataset, allowing for comparison of performance across models of similar scale. The best and second-best performing models within each size category are highlighted for easy identification.
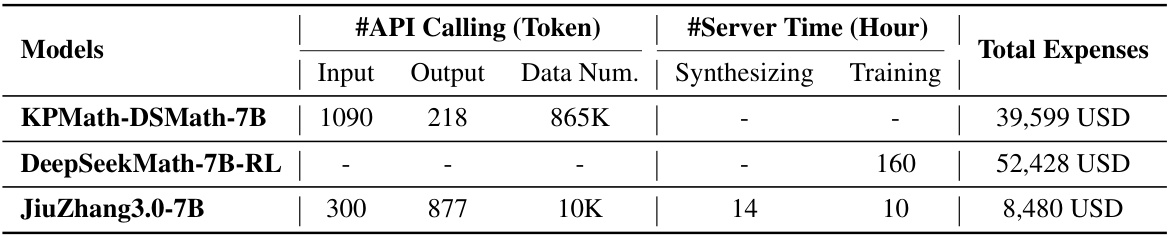
This table presents a cost comparison of training three different large language models (LLMs) for mathematical reasoning. It breaks down the costs into two components: using the OpenAI GPT-4 API for data synthesis, and renting AWS GPU servers for model training. The table shows the number of API calls (broken down by input and output tokens), the number of data points synthesized, and the server time required for synthesis and training for each model. Finally, it provides the total estimated cost in USD for each LLM.
Full paper#