TL;DR#
Multi-unit uniform price auctions are commonly used in various markets, including electricity markets, but strategic bidding by participants makes it challenging to design efficient learning algorithms for resource allocation. Existing algorithms for online bidding in these auctions often yield high regret rates, especially under bandit feedback where bidders only observe their own outcomes. This research focuses on online learning in repeated multi-unit uniform price auctions.
This paper introduces a novel representation of the bid space and leverages its structure to develop a new learning algorithm. The algorithm achieves a significantly improved regret bound of Õ(K4/3T2/3) under bandit feedback and Õ(K5/2√T) under a novel “all-winner” feedback model. The improved regret rates are shown to be tight up to logarithmic terms, bridging the gap between the performance under full information and bandit feedback. The proposed approach demonstrates improved performance for online bidding strategies in a variety of auctions and resource allocation scenarios.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in auction theory and online learning because it significantly improves the regret bounds in multi-unit uniform price auctions under various feedback settings. It offers novel approaches to modeling the bid space and feedback mechanisms, opening new avenues for research in online resource allocation and strategic bidding, particularly relevant to electricity markets.
Visual Insights#

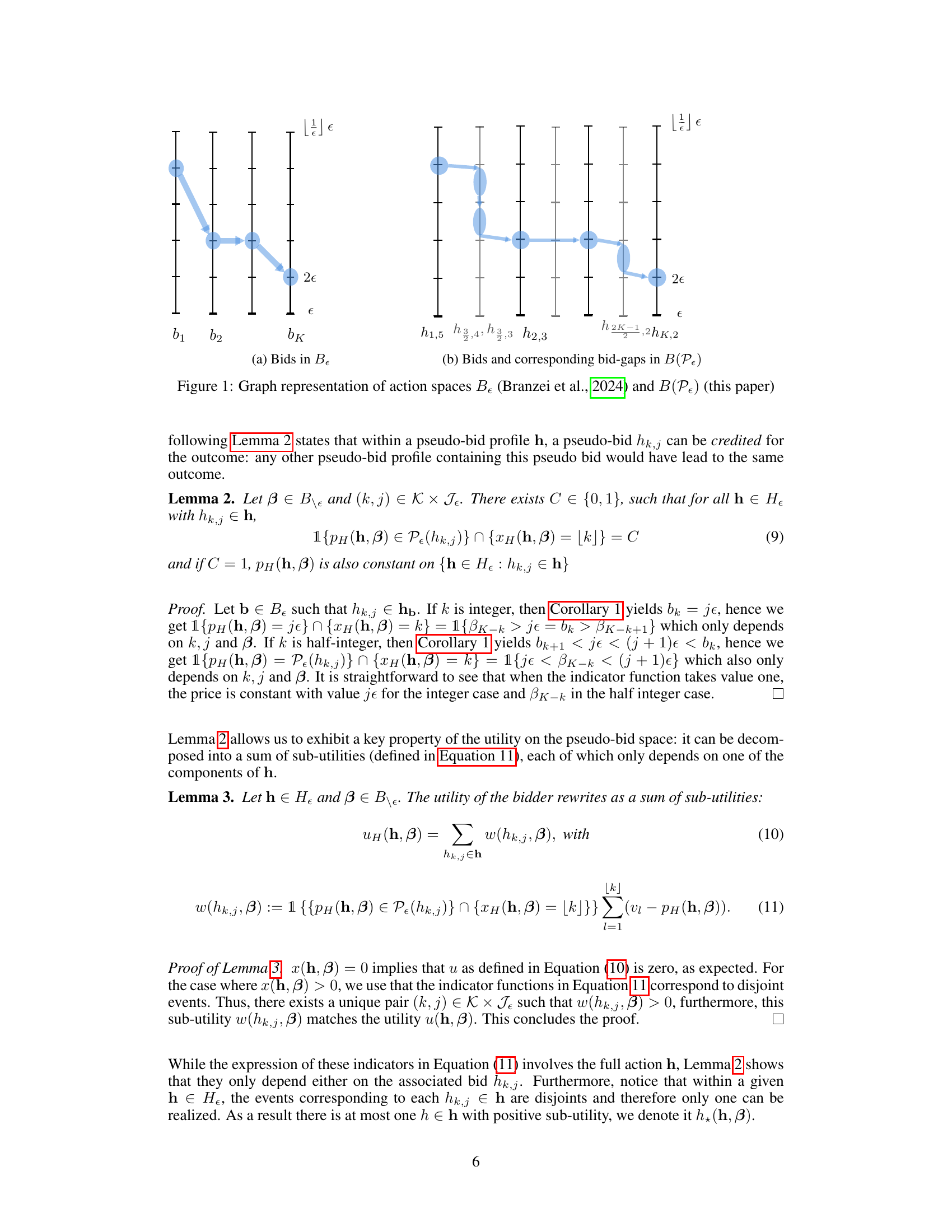
🔼 This figure shows how two corresponding bids are represented in the original action space B (Branzei et al., 2024) and in the new action space B(Pɛ) introduced in this paper. The bids are represented by circles, while the bid-gaps are represented by ellipses. The figure helps to visualize the differences between the two action spaces and how the new action space leverages the regularity of the utility function.
read the caption
Figure 1: Graph representation of action spaces Bɛ (Branzei et al., 2024) and B(PE) (this paper)

🔼 This table summarizes the regret rates achieved by the proposed algorithm under different feedback settings (full information, all-winner, and bandit) in a multi-unit uniform price auction. It compares the regret bounds obtained in this work to those previously reported in the literature and also provides lower bounds on the regret for each feedback setting. The asterisk indicates that the lower bound for the bandit feedback holds specifically for the Last Accepted Bid (LAB) pricing rule.
read the caption
Table 1: Regret Rates in multi-unit uniform price auction. * holds in the LAB pricing rule setting
Full paper#