↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Federated learning (FL) often struggles with nonconvex problems, especially when data is spread across multiple devices (clients). Existing methods either fail to handle manifold constraints effectively or are computationally expensive, and many lack theoretical guarantees. Furthermore, handling heterogeneous data distribution among clients is challenging. Traditional methods face problems such as the server model not lying on the manifold after averaging or high communication and computation costs to correct client drift.
This research introduces a novel algorithm to address these limitations. It cleverly uses stochastic Riemannian gradients and manifold projection to maintain computational efficiency and model feasibility. Local updates reduce communication overhead, and correction terms effectively combat client drift. Rigorous theoretical analysis demonstrates sublinear convergence, proving the algorithm’s robustness. The algorithm outperforms existing methods in numerical experiments on kPCA and low-rank matrix completion tasks.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in federated learning and manifold optimization. It bridges the gap between these two fields, offering an efficient and effective algorithm for nonconvex problems common in machine learning. The theoretical analysis and numerical experiments demonstrate its superiority over existing methods. It also opens new avenues for research in heterogeneous data handling and communication-efficient FL.
Visual Insights#

This figure compares the performance of four algorithms (RFedavg, RFedprox, RFedSVRG, and the proposed algorithm) for solving the kPCA problem using the MNIST dataset. The y-axis represents the norm of the Riemannian gradient (||gradf(x’)||), a measure of how close the algorithm is to a solution. The x-axis shows the number of communication rounds, the total communication quantity (number of matrices transmitted), and the runtime in seconds. The figure visually demonstrates that the proposed algorithm converges significantly faster and requires less communication than the alternatives.
In-depth insights#
Manifold FL#
Manifold Federated Learning (Manifold FL) presents a novel approach to address the challenges of training machine learning models on data residing on decentralized devices while adhering to complex, non-convex constraints. Traditional federated learning struggles with manifold-constrained problems because averaging local models often violates the manifold’s structure. Manifold FL directly tackles this issue by employing techniques such as Riemannian optimization and manifold projection operators, ensuring that model updates remain within the feasible space. This methodology promises improvements in model accuracy and efficiency by leveraging the inherent geometric properties of the data. A key advantage is the ability to handle heterogeneous data distributions across devices, a common hurdle in real-world federated learning scenarios. However, the theoretical analysis of Manifold FL is complex due to the non-convex nature of manifold optimization, necessitating novel mathematical tools to prove convergence. Practical implementations of Manifold FL might also face challenges related to computational costs associated with Riemannian operations and the need for efficient manifold projection techniques. Further research is needed to address these practical considerations and to explore the scalability and robustness of Manifold FL in diverse applications.
Algo Efficiency#
The algorithm’s efficiency is a central theme, focusing on minimizing both computational and communication overheads. Stochastic Riemannian gradients are employed to efficiently handle the manifold constraints, avoiding expensive geometric operations like the exponential map. Local updates reduce communication frequency between clients and server. A novel correction term efficiently addresses the ‘client drift’ problem, common in federated learning, without excessive communication. The algorithm’s efficiency is further validated by numerical experiments demonstrating significantly lower computational and communication costs than existing methods, particularly for high-dimensional problems like kPCA and LRMC. This overall approach prioritizes practicality and scalability in a distributed setting.
Convergence#
The convergence analysis within the paper is a critical component, demonstrating the algorithm’s ability to reach a solution efficiently. The theoretical analysis establishes sub-linear convergence to a neighborhood of a first-order optimal solution. This result is particularly significant because it addresses the complexities of nonconvex optimization on manifolds, a challenging problem in federated learning. The analysis cleverly leverages the manifold’s geometric properties and the loss function’s characteristics, providing a novel approach for this type of problem. Furthermore, the convergence rate is shown to depend on factors such as sampling variance and algorithm parameters. The paper’s numerical experiments further support these theoretical findings, showcasing the practical effectiveness of the algorithm compared to existing methods. A key strength is that the analysis accommodates an arbitrary number of local updates and full client participation, overcoming limitations of prior work. The inclusion of a detailed convergence analysis is crucial for establishing the algorithm’s reliability and validating its effectiveness in practical applications.
Experiments#
The Experiments section of a research paper is crucial for validating the claims made. A strong Experiments section will detail the experimental setup, including datasets used, metrics employed for evaluation, and the specific implementation details of any algorithms or models. It’s essential to demonstrate reproducibility by providing sufficient detail so that other researchers can repeat the experiments. Statistical significance should be carefully considered, and results should be presented with appropriate error bars or confidence intervals. The selection of baselines for comparison is also important, as it can significantly impact the interpretation of results. Robustness testing of the proposed methods against variations in datasets, parameters or experimental conditions strengthens the results. A clear presentation and analysis of results are vital to ensure readers can readily interpret the findings, and any limitations or potential biases of the experiment should be transparently acknowledged.
Future Work#
The “Future Work” section of this research paper on federated learning on manifolds presents several promising avenues. Extending the theoretical analysis to handle more complex scenarios, such as non-smooth manifolds or non-convex loss functions with stronger assumptions, would significantly enhance its practical applicability. Investigating adaptive step-size strategies that dynamically adjust to the manifold’s curvature or data heterogeneity could improve convergence speed and robustness. Exploring different manifold projection operators optimized for specific manifold structures and evaluating their impact on computational efficiency is crucial. Addressing the challenges of client drift in practical settings with highly heterogeneous data and exploring other variance reduction techniques would be valuable. Finally, a comprehensive empirical evaluation on larger datasets and in diverse real-world applications, like PCA and low-rank matrix completion, is needed to confirm the robustness and scalability of this algorithm.
More visual insights#
More on figures
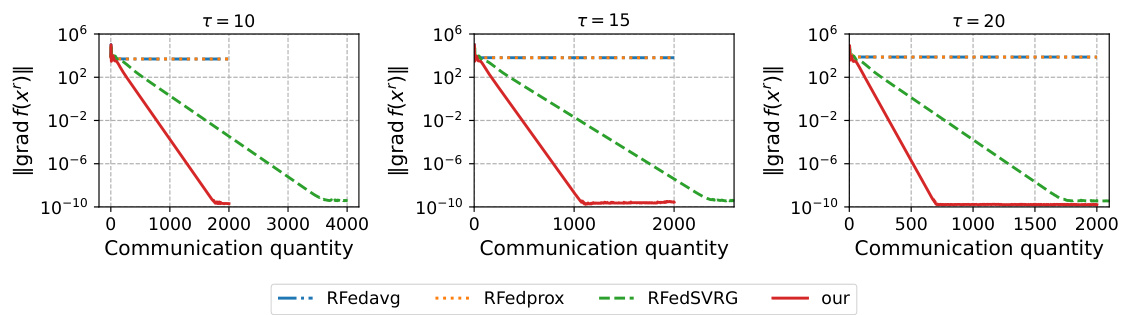
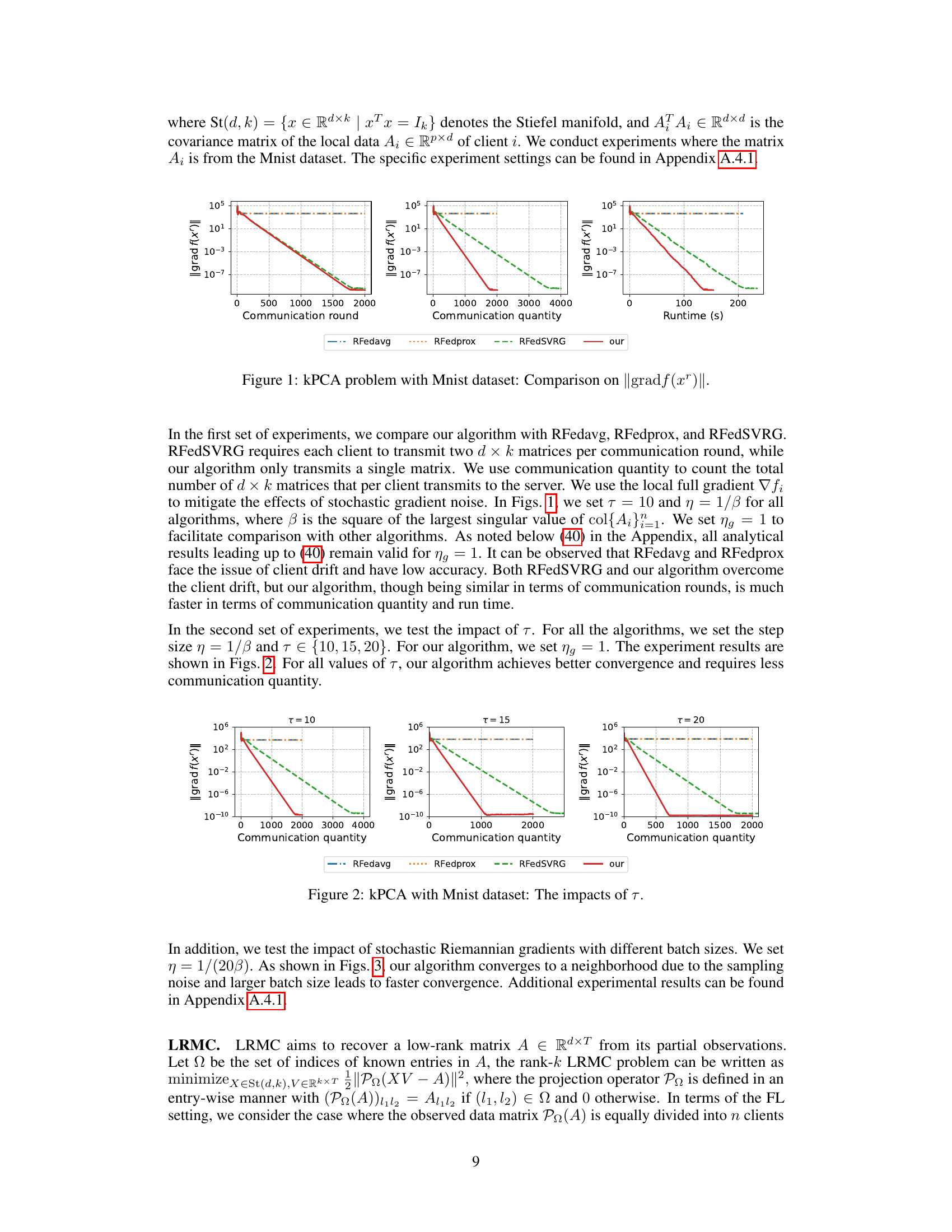
This figure shows the impact of the number of local updates (τ) on the convergence speed of the proposed algorithm and other baseline algorithms (RFedAvg, RFedprox, RFedSVRG). It demonstrates that increasing τ leads to faster convergence, and the proposed algorithm consistently outperforms the baselines in terms of communication quantity needed to achieve a certain level of accuracy.

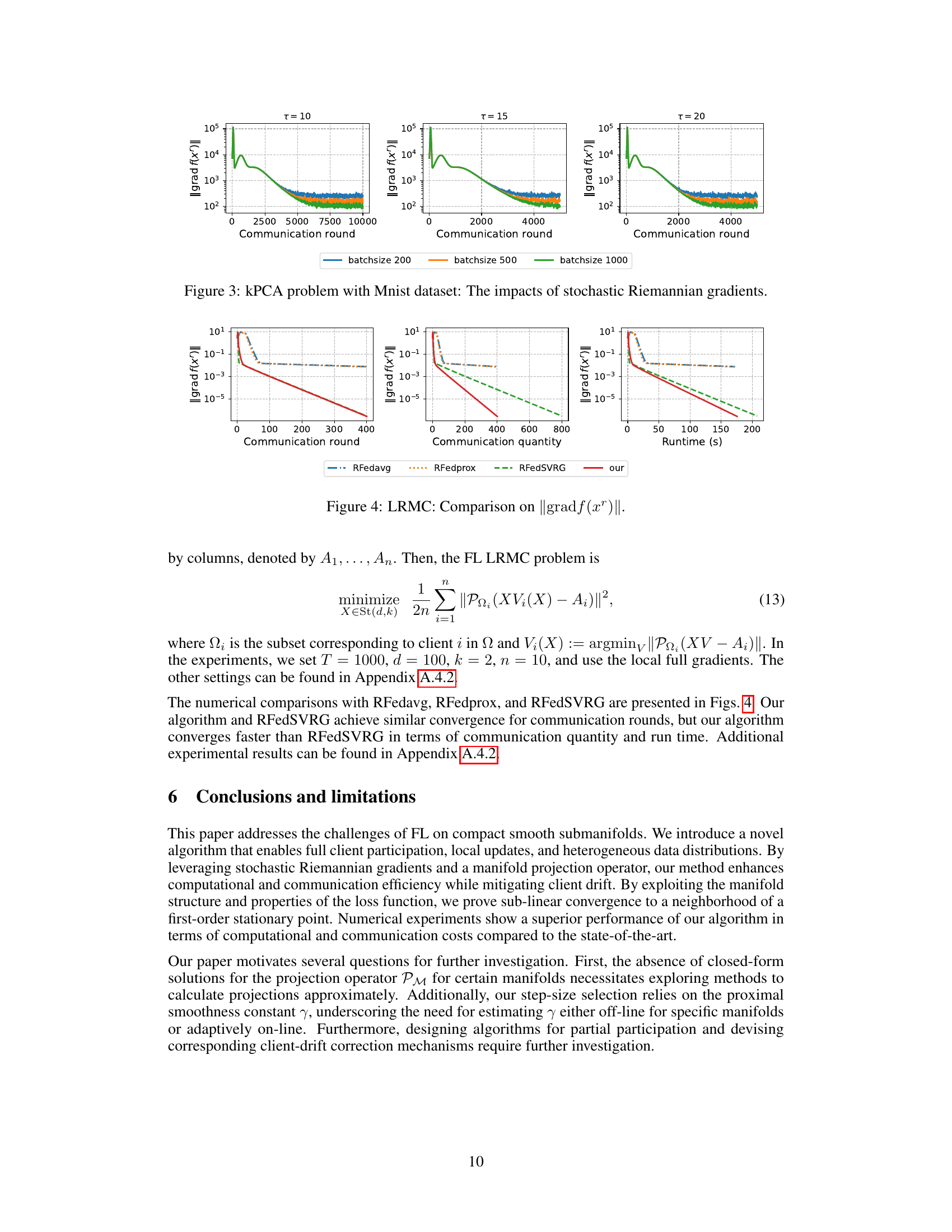
This figure shows the impact of using stochastic Riemannian gradients with different batch sizes (200, 500, and 1000) on the convergence of the kPCA algorithm. The plots illustrate the norm of the Riemannian gradient (||grad f(x’)||) over communication rounds for different values of τ (the number of local updates per client). It demonstrates how varying the batch size affects the convergence speed and the overall accuracy of the algorithm when dealing with stochasticity.
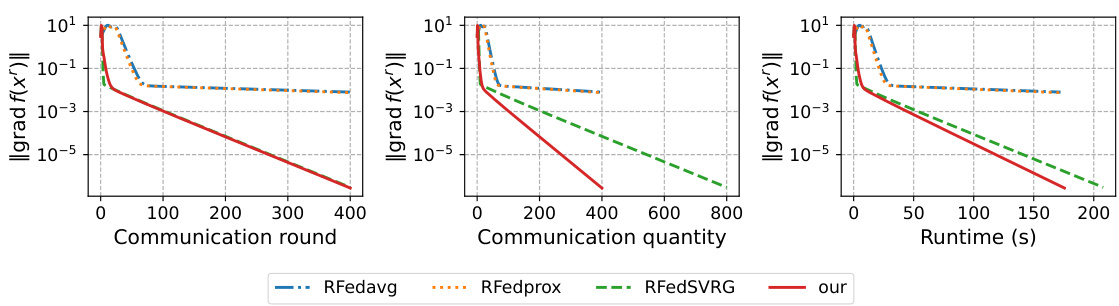
This figure compares the performance of four different federated learning algorithms (RFedavg, RFedprox, RFedSVRG, and the proposed algorithm) on the kPCA problem using the MNIST dataset. The y-axis shows the norm of the Riemannian gradient, which indicates the convergence of the algorithms. The x-axis is shown with three different units: communication rounds, communication quantity, and runtime. The figure demonstrates that the proposed algorithm converges faster and requires fewer communication resources than the other three algorithms.

This figure compares the performance of four algorithms (RFedavg, RFedprox, RFedSVRG, and the proposed algorithm) for solving the kPCA problem using the MNIST dataset. The x-axis represents communication rounds, communication quantity, and runtime (s). The y-axis shows the value of f(x) - f*, which represents the difference between the objective function value and the optimal value. The figure demonstrates that the proposed algorithm converges faster and achieves lower f(x) - f* values compared to the other algorithms.

This figure compares the performance of four different algorithms (RFedavg, RFedprox, RFedSVRG, and the proposed algorithm) for solving the kPCA problem using the MNIST dataset. The y-axis shows the norm of the Riemannian gradient (||gradf(x’)||), a measure of the algorithm’s convergence towards a solution. The x-axis represents the number of communication rounds for RFedavg, RFedprox and our algorithm; it represents the communication quantity for RFedavg, RFedprox and RFedSVRG; it represents the runtime for RFedSVRG and our algorithm. The results show that the proposed algorithm converges faster and achieves a lower gradient norm compared to the other algorithms, indicating improved efficiency and accuracy.

This figure shows the impact of the number of local updates τ on the convergence of the KPCA algorithm with a synthetic dataset. The results are presented for τ = 10, τ = 15, and τ = 20. The plots show that as τ increases, the convergence becomes faster. For all values of τ, the proposed algorithm achieves high accuracy and requires less communication.
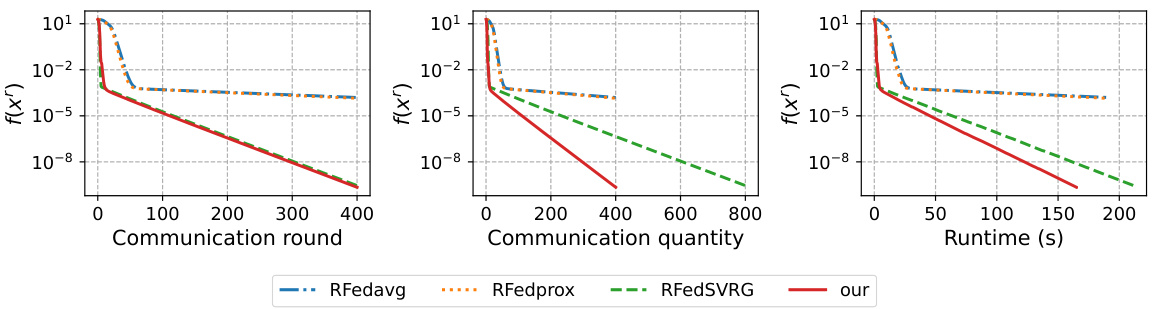
This figure compares the performance of four different federated learning algorithms (RFedavg, RFedprox, RFedSVRG, and the proposed algorithm) on the task of kernel principal component analysis (kPCA) using the MNIST dataset. The y-axis represents the norm of the Riemannian gradient, which is a measure of convergence. The x-axis shows the communication rounds, communication quantity, and runtime. The results indicate that the proposed algorithm converges faster and requires significantly less communication than the other algorithms.
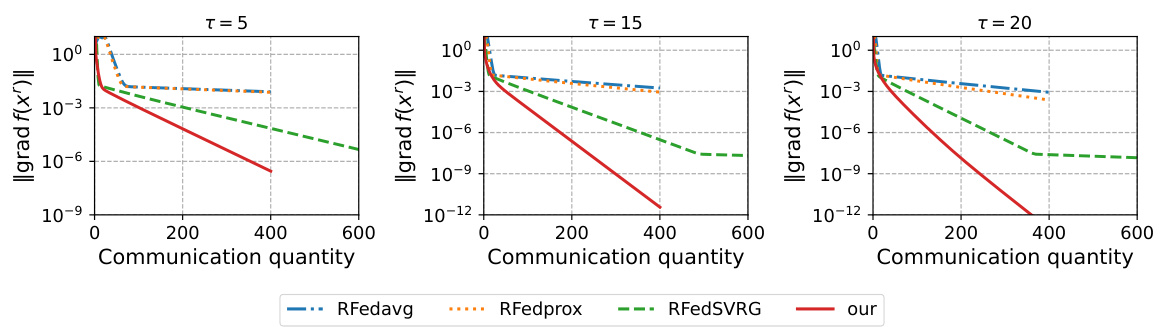
This figure shows the impact of the number of local updates τ on the convergence of the kPCA algorithm with a synthetic dataset. The plots show the norm of the Riemannian gradient ||grad f(xr)|| versus the communication quantity for three different values of τ (10, 15, and 20). The results demonstrate that increasing τ leads to faster convergence and requires less communication.

This figure compares the performance of four algorithms (RFedavg, RFedprox, RFedSVRG, and the proposed algorithm) for solving the kPCA problem using the MNIST dataset. The y-axis represents the norm of the Riemannian gradient, ||gradf(x’)||, which is a measure of how close the current solution is to optimality; a lower value indicates a better solution. The x-axis shows the communication rounds, communication quantity, and runtime. The figure shows that the proposed algorithm achieves a smaller Riemannian gradient norm than other algorithms, suggesting better convergence and solution quality, with significantly lower computational and communication overheads.
Full paper#