↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Training large language models (LLMs) involves computationally intensive forward and backward computations. Previous research focused on the forward step, but LLM training efficiency also depends heavily on the speed of backward computation (gradient calculation). The size of the entries in the model’s parameter matrices plays a significant role in determining the training time. This paper addresses the challenges of the backward step, which is significantly more complex than the forward step.
The researchers developed a novel algorithm that efficiently calculates the gradient for the backward step. They also proved that the same computational threshold observed in the forward step exists in the backward step, confirming that the complexity of both forward and backward computations has a similar computational boundary based on matrix entries. This result completely characterizes the fine-grained complexity of LLM training, providing both upper and lower bounds for each training step, which will directly improve LLM training and scalability.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in large language model (LLM) training because it provides a complete characterization of the fine-grained complexity of both forward and backward computation steps. This understanding enables the design of faster algorithms and provides theoretical limits for further improvement. It is relevant to the current trend of optimizing LLM training efficiency and opens avenues for exploring new algorithms and lower bounds in related computational problems.
Visual Insights#
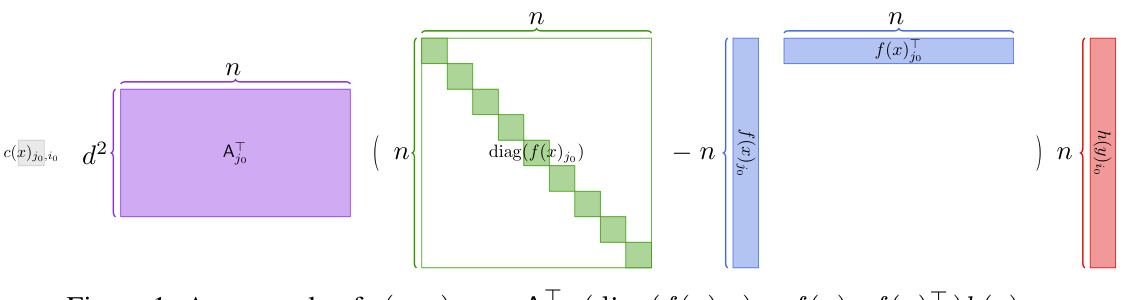
This figure illustrates the computation of c(x, y)jo,io, a key component in calculating the gradient of the attention loss function. The diagram shows the matrix multiplication involved, highlighting the use of diag(f(x)jo) and f(x)jo f(x)T, which represent a diagonal matrix and a rank-one matrix respectively. These matrices are combined with Ajo and h(y)io using matrix multiplication to arrive at the final result, c(x, y)jo,io.
Full paper#