On the Necessity of Collaboration for Online Model Selection with Decentralized Data

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it addresses a critical gap in online model selection, specifically when data is decentralized. By establishing theoretical lower and upper bounds on regret, and proposing a novel federated algorithm, it provides valuable guidance on the necessity and effectiveness of collaborative approaches in various settings. This has significant implications for optimizing resource usage and achieving improved performance in real-world applications.

Visual Insights

#

The table compares the proposed algorithm, FOMD-OMS, with two existing federated online multi-kernel learning algorithms, eM-KOFL and POF-MKL. It shows that FOMD-OMS achieves a better regret bound (a measure of performance) with lower time and communication complexity than the other methods. The time complexity is the computational cost per round on each client, while download (bits) shows the amount of data transmitted from server to clients.

This table compares the proposed algorithm, FOMD-OMS, with two existing federated online multi-kernel learning algorithms, eM-KOFL and POF-MKL. The comparison includes the regret bound, per-round time complexity on the client, and the communication cost (download). It highlights that FOMD-OMS achieves a better regret bound and lower computational and communication costs than the other two algorithms.

In-depth insights

#

OMS-DecD Necessity

#

The necessity of collaboration in online model selection with decentralized data (OMS-DecD) is a central question explored in this research. The authors challenge the prevalent assumption that federated learning inherently requires collaboration, arguing that its necessity is contingent upon computational constraints imposed on individual clients. Without these constraints, collaboration offers minimal benefit; a non-collaborative approach, where each client performs model selection independently, suffices. However, when client computational resources are limited (o(K), where K is the number of hypothesis spaces), collaboration becomes essential to achieve optimal regret bounds. This nuanced perspective shifts the focus from merely comparing collaborative and non-collaborative algorithms to understanding their efficacy under specific resource limitations, providing a valuable framework for future algorithm design in decentralized settings.

Regret Bound Analysis

#

Regret bound analysis is crucial in online learning, providing a measure of an algorithm’s performance against an optimal solution. A tight regret bound demonstrates the algorithm’s efficiency and effectiveness. In this context, a key focus would be on the derivation of both upper and lower bounds. Upper bounds represent the worst-case performance guarantee, while lower bounds establish the best achievable performance under given conditions. A smaller gap between these bounds indicates a more precise understanding of algorithm behavior. Furthermore, the analysis should consider the impact of various parameters like the number of clients (M) and the number of hypothesis spaces (K) on the regret. The analysis might explore how communication costs influence regret, possibly leading to trade-offs between communication efficiency and regret minimization. Analyzing the dependence of regret on other parameters like the dimensionality of data or the type of loss function would be another significant aspect of the regret bound analysis. Finally, the comparison of the obtained regret bounds with those of existing algorithms highlights the novelty and potential advantages of the proposed approach. A high probability regret bound strengthens the result by providing a probabilistic guarantee on the performance of the algorithm.

Federated Algorithm

#

The research paper explores federated learning algorithms in the context of online model selection with decentralized data. A crucial aspect is the design of a federated algorithm that effectively balances the goals of minimizing regret (error in model selection) and respecting privacy constraints inherent in decentralized settings. The paper likely presents a novel federated algorithm, potentially based on online mirror descent or a similar optimization technique, adapted for the specific challenge of selecting models from multiple hypothesis spaces across various clients. The algorithm’s design needs to address the trade-off between communication efficiency (minimizing the data exchanged between clients and a central server) and the accuracy of the selected model. This is achieved via careful techniques like model averaging, gradient aggregation, or intermittent communication, which are standard in federated learning, and the specifics of these techniques are a key contribution of the paper. The algorithm’s performance is rigorously analyzed through theoretical regret bounds which will quantify how well it adapts to various challenges in decentralized data, and finally, the paper likely validates its findings through empirical evaluations.

Computational Limits

#

The concept of ‘Computational Limits’ in the context of online model selection with decentralized data is crucial. It investigates the inherent trade-offs between collaboration among clients and the computational resources available to each. The analysis reveals that without computational constraints, collaboration is unnecessary; individual clients can effectively perform model selection independently. However, when computational resources are limited (e.g., memory or processing power), collaboration becomes essential to achieve optimal model selection, reducing the individual burden and improving overall performance. This highlights the practical considerations in designing federated learning algorithms, demonstrating that the ideal approach adapts to the specifics of the client’s computational capabilities. A key finding is the lower bound on regret that highlights the fundamental limits of non-cooperative algorithms under constrained resources. The research elegantly bridges theoretical analysis and practical considerations, providing valuable insight into the design and optimization of real-world federated learning systems.

Distributed OMKL

#

Distributed Online Multi-Kernel Learning (OMKL) presents a significant challenge in machine learning, demanding efficient model selection and prediction in decentralized data scenarios. Collaboration among clients is crucial for effective distributed OMKL when computational resources are limited. The paper investigates the necessity of collaboration by establishing lower and upper bounds on the regret, highlighting the trade-off between communication overhead and computational constraints. The analysis reveals that collaboration isn’t always necessary, particularly when clients possess ample computational capacity. However, if client-side computation is constrained, collaborative strategies become crucial for optimal regret bounds. The proposed Federated Online Mirror Descent (FOMD) algorithm, tailored for this distributed setting, demonstrates improvements over existing methods by achieving better regret and reduced communication costs, offering a more efficient approach for model selection and prediction in resource-scarce environments. The algorithm’s success relies on decoupling model selection and prediction tasks, thereby optimizing both accuracy and efficiency. The work ultimately provides valuable insights into the inherent trade-offs involved in designing efficient and effective algorithms for distributed OMKL.

More visual insights

#

More on tables

This table compares the proposed FOMD-OMS algorithm with two existing federated online multi-kernel learning (OMKL) algorithms: eM-KOFL and POF-MKL. The comparison includes the regret bound achieved by each algorithm, the per-round time complexity on a single client, and the communication cost (in bits) for downloading information from the server. The table highlights that FOMD-OMS offers improvements in both computational cost and communication overhead compared to the existing methods.

The table compares the proposed FOMD-OMS algorithm with two previously published federated online multi-kernel learning algorithms (eM-KOFL and POF-MKL) in terms of regret bound, per-round time complexity on client, and communication cost (download in bits). It highlights that FOMD-OMS offers improved regret bounds and reduced computational and communication costs compared to existing methods.

This table compares the proposed FOMD-OMS algorithm with two existing federated online multi-kernel learning (OMKL) algorithms, eM-KOFL and POF-MKL. The comparison includes the regret bound achieved by each algorithm, the per-round time complexity on each client, and the communication cost (in bits) for downloading model parameters. The results highlight that FOMD-OMS achieves a better regret bound with significantly lower computational and communication costs than the other two algorithms.

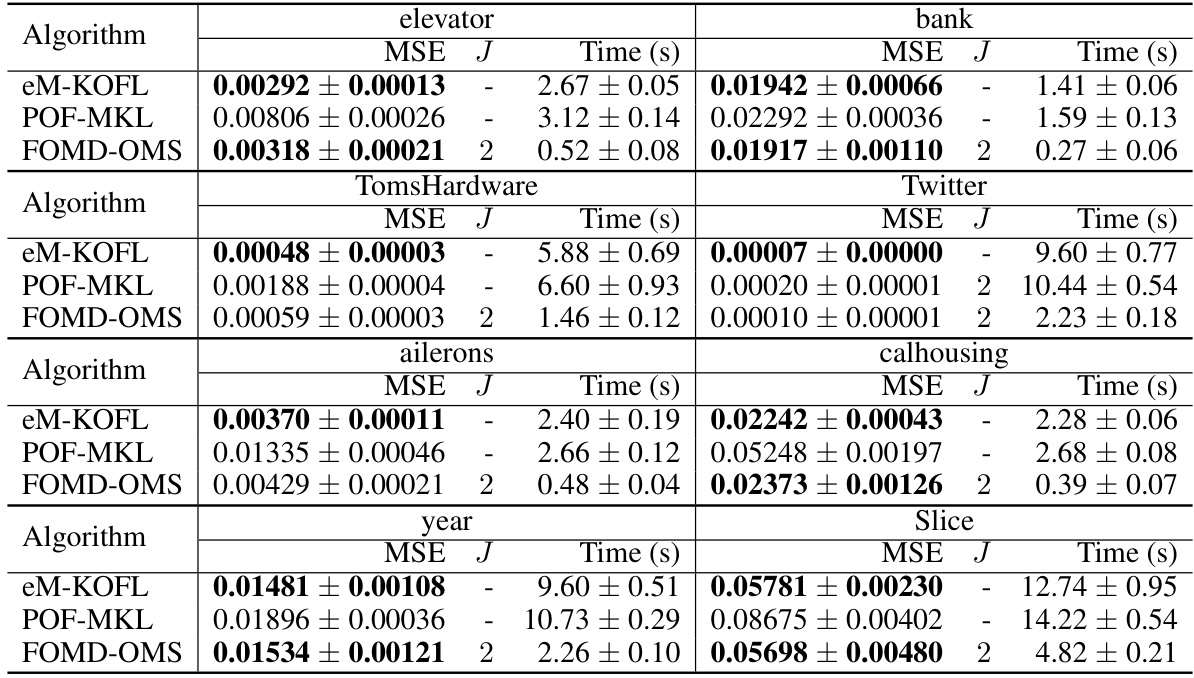
The table compares the proposed FOMD-OMS algorithm with two existing federated online multi-kernel learning (OMKL) algorithms, eM-KOFL and POF-MKL. It shows the regret bounds, per-round time complexity on the client, and download cost (in bits) for each algorithm. The results highlight that FOMD-OMS achieves better regret bounds and lower computational and communication costs than the existing algorithms.

Full paper

#