TL;DR#
Diffusion models are powerful generative models, but their efficiency relies on accurate score estimation. Recent work shows that sampling from an unknown distribution can be reduced to accurate score estimation, but this leaves open the question of how computationally hard it is to estimate these scores. Estimating score functions for complex high-dimensional distributions is challenging and computationally expensive; this makes it impossible to efficiently implement this process for certain distributions.
This paper addresses this issue by demonstrating that L²-accurate score estimation is computationally hard, even when ample samples are available. The authors achieve this by creating a reduction from the Gaussian Pancakes problem (known to be computationally hard under reasonable assumptions) to the score estimation problem. This provides a new understanding of the computational limits of score estimation, and suggests that future research should focus on alternative approaches to sampling or on stronger assumptions about data distributions to make score estimation feasible.
Key Takeaways#
Why does it matter?#
This paper is crucial because it reveals a computational barrier in a widely used machine learning technique, score estimation. This has significant implications for the development of efficient algorithms in generative modeling and post-quantum cryptography, paving the way for more realistic expectations and research directions. The reduction from Gaussian Pancakes problem to L2-accurate score estimation highlights the inherent complexity, urging researchers to explore alternative algorithms or stronger assumptions.
Visual Insights#
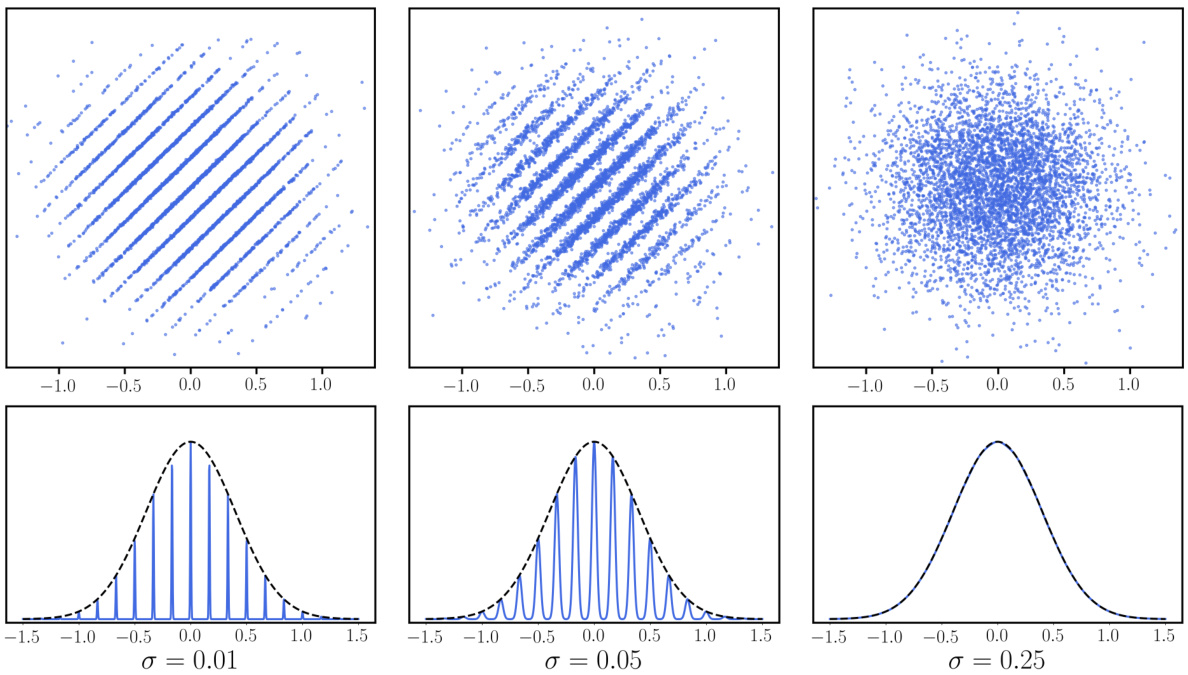
🔼 This figure visualizes 2D Gaussian Pancakes distributions with different thickness parameters (σ). The top row shows scatter plots of samples from the distributions, illustrating how the distribution changes from a clear pancake structure to a more Gaussian-like distribution as σ increases. The bottom row shows the probability density functions along the secret direction u, comparing the Gaussian Pancakes with the standard Gaussian.
read the caption
Figure 1: Top: Scatter plot of 2D Gaussian pancakes Pu with secret direction u = (-1/√2, 1/√2), spacing y = 6, and thickness σ∈ {0.01, 0.05, 0.25}. Bottom: Re-scaled probability densities of Gaussian pancakes (blue) for each σ∈ {0.01, 0.05, 0.25} and the standard Gaussian (black) along u.
Full paper#