↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Large language models require substantial computational resources for fine-tuning. Existing parameter-efficient fine-tuning (PEFT) methods, while efficient, often suffer from accuracy losses compared to full fine-tuning. This necessitates a trade-off between efficiency and accuracy. This paper addresses the limitations of existing PEFT methods by proposing a new approach.
The proposed method, Singular Vectors Fine-Tuning (SVFT), updates the model’s weights using a sparse combination of its singular vectors. By carefully controlling the sparsity of the update, SVFT achieves a superior balance between parameter efficiency and performance. Experiments across various language and vision benchmarks demonstrate that SVFT recovers up to 96% of full fine-tuning performance while only training 0.006% to 0.25% of the parameters, a significant improvement over existing methods.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel parameter-efficient fine-tuning method, SVFT, that significantly outperforms existing methods in terms of accuracy and parameter efficiency. It offers a new approach to model adaptation, opening avenues for research in efficient large model training and deployment. The theoretical analysis and empirical results provide valuable insights for researchers working on related problems.
Visual Insights#
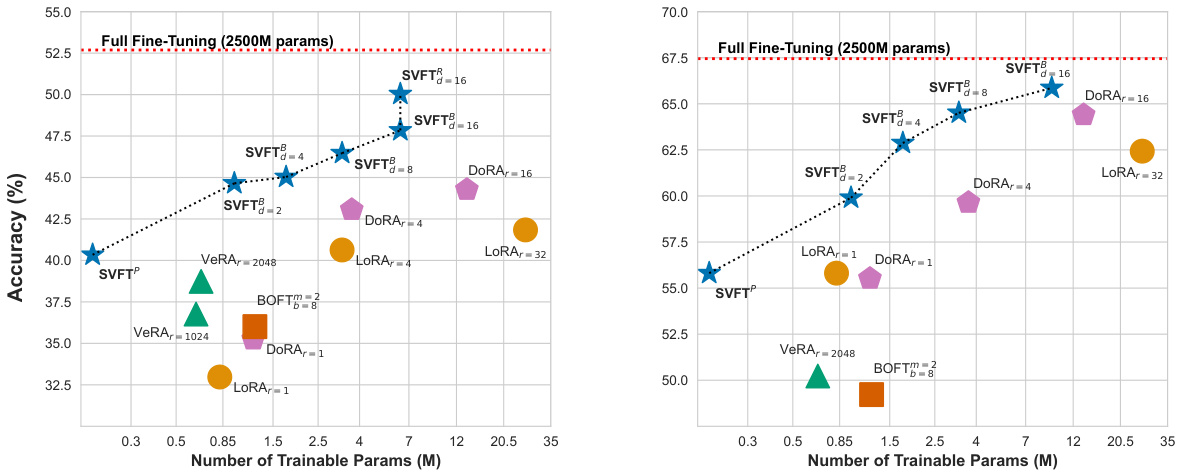
This figure compares the performance (accuracy) of various parameter-efficient fine-tuning (PEFT) methods against the number of trainable parameters required. The left panel shows results on the GSM-8K benchmark, while the right panel shows results on a commonsense reasoning benchmark. Both use the Gemma-2B language model. The figure demonstrates that SVFT achieves higher accuracy than competing methods (like LoRA and DORA) while using significantly fewer trainable parameters. Specifically, SVFT and its random variant (SVFT/R) outperform DoRA with 8 and 16 ranks using 75% fewer parameters.
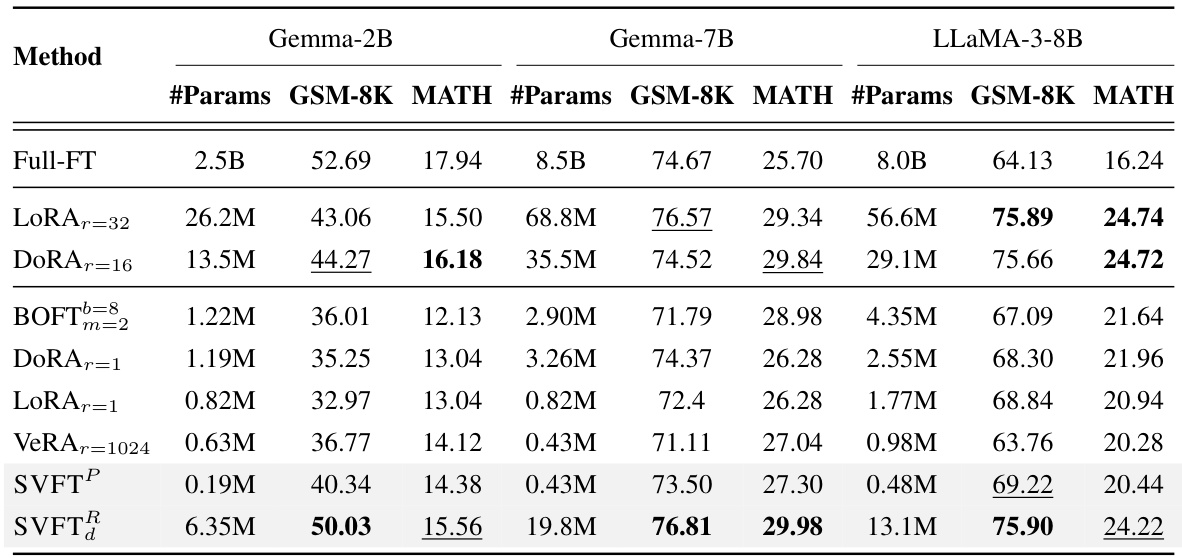
This table presents the performance (accuracy) achieved by various parameter-efficient fine-tuning (PEFT) methods and full fine-tuning on two mathematical reasoning benchmarks: GSM-8K and MATH. The performance is measured in terms of accuracy. The table also shows the number of trainable parameters used by each method. The results highlight SVFT’s superior or competitive performance while using significantly fewer parameters compared to other PEFT techniques.
In-depth insights#
SVFT: Core Concept#
SVFT (Singular Vectors Fine-Tuning) presents a novel parameter-efficient fine-tuning method. Its core concept revolves around structuring the update (ΔW) to a pre-trained weight matrix (W) as a sparse combination of W’s singular vectors (U and V). Instead of learning a large number of parameters directly, SVFT focuses on learning a smaller set of coefficients (M) that weight these singular vectors. This approach is particularly efficient because it leverages the pre-trained model’s existing structure, only learning the necessary adjustments. The sparsity of M is crucial, enabling a trade-off between the number of trainable parameters and model expressivity. This contrasts with methods like LoRA, which use low-rank approximations that might not fully capture the necessary expressiveness. By carefully controlling the sparsity pattern and choosing among different sparsity patterns(Plain, Random, Banded, Top-k), SVFT achieves a balance between accuracy and efficiency, potentially outperforming existing methods. The method’s inherent structure also implies a higher rank update than comparables for the same parameter budget. The key innovation lies in using the singular vectors of the pre-trained weights to guide the fine-tuning process, which directly relates to the pre-trained model’s underlying structure, offering potential advantages over methods ignoring this pre-existing information.
Sparsity Pattern#
The concept of a ‘sparsity pattern’ within the context of parameter-efficient fine-tuning (PEFT) methods like SVFT is crucial for balancing model performance and computational efficiency. SVFT leverages the inherent structure of a weight matrix W by updating it as a sparse combination of its singular vectors. This sparsity is controlled by a pre-determined pattern (Ω) dictating which elements of the trainable matrix M are non-zero. Different sparsity patterns are explored, such as ‘Plain’ (diagonal M), ‘Banded’ (off-diagonal elements included), ‘Random’, and ‘Top-k’, each offering a different trade-off. The choice of sparsity pattern directly impacts the rank of the update, expressivity, and the number of trainable parameters. A denser pattern allows for greater expressiveness, potentially capturing more of the full fine-tuning performance, but at the cost of increased computational complexity. The study of these patterns is key to understanding SVFT’s effectiveness and optimizing its performance for various downstream tasks and computational budgets.
Method Variants#
The concept of “Method Variants” in a research paper typically explores different modifications or adaptations of a core methodology. Analyzing such variants reveals crucial insights into the method’s robustness, flexibility, and limitations. A thoughtful exploration would examine the rationale behind each variant, assessing the changes made to the original method and their impact on performance and efficiency. For instance, some variants might simplify the original approach for increased ease of implementation, while others may enhance its complexity to handle more nuanced datasets or tasks. It’s critical to evaluate the trade-offs associated with each variant, such as computational cost versus performance gains. A rigorous analysis needs to go beyond simply comparing results across variants; instead, it should delve into why certain variants perform better or worse under specific conditions. Ultimately, a strong analysis of method variants will illuminate the method’s strengths, expose its vulnerabilities, and highlight its adaptability across different scenarios, providing a clearer picture of its overall value and potential.
Empirical Analysis#
An Empirical Analysis section of a research paper would delve into the experimental results, providing a thorough examination of the data collected. It would likely begin by describing the experimental setup, including datasets, model architectures, and evaluation metrics. Then, it would present the key findings in a clear and concise manner, using tables, figures, and statistical analyses to support claims. A key aspect would be comparing the performance of the proposed method against existing state-of-the-art methods, highlighting any significant improvements or advantages. Furthermore, a discussion of potential limitations or unexpected outcomes would demonstrate a nuanced understanding of the study’s findings. This section should also discuss the statistical significance of the results, addressing potential biases or confounding factors that may have influenced the outcomes. Finally, a robust empirical analysis would include error bars or confidence intervals, demonstrating the reliability and generalizability of the results. The analysis should go beyond mere reporting of numbers, offering insightful interpretations and drawing connections between empirical evidence and theoretical underpinnings. This would lead to a strong conclusion that clearly summarizes the key findings and their implications.
Future of SVFT#
The future of SVFT (Singular Vectors Fine-Tuning) looks promising, particularly in addressing the limitations of current parameter-efficient fine-tuning (PEFT) methods. Further exploration of different sparsity patterns in the trainable matrix M could unlock even greater performance gains, potentially achieving near full fine-tuning performance with even fewer parameters. Investigating adaptive sparsity learning algorithms, which could automatically determine the optimal sparsity pattern during training, would significantly enhance the method’s efficiency and adaptability. Additionally, research should focus on reducing memory consumption. This could involve exploring techniques like quantization, low-rank approximations of singular vectors, or alternative matrix factorization methods. Finally, extending SVFT’s applicability to diverse model architectures, beyond transformers and vision models, and exploring its effectiveness in other domains, such as reinforcement learning, would further broaden its impact. Theoretical analysis to establish stronger performance guarantees would also enhance confidence in the method’s efficacy.
More visual insights#
More on figures
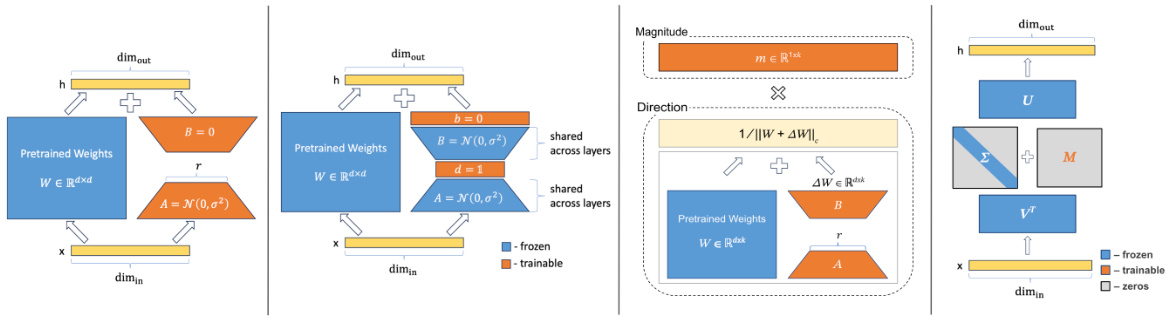
This figure schematically compares four parameter-efficient fine-tuning (PEFT) methods: LoRA, VeRA, DORA, and SVFT. Each method is illustrated with a diagram showing how it updates the pretrained weight matrix (W). LoRA uses low-rank matrices (B and A) to update W. VeRA employs trainable diagonal matrices (Ab and Ad) with shared random matrices. DORA decomposes W into magnitude and direction components, updating only the direction with low-rank matrices. SVFT updates W using a sparse combination of its singular vectors (U and V), training only the coefficients (M) of these combinations. The diagrams highlight the differences in the structure of the update matrices and the number of trainable parameters in each method.
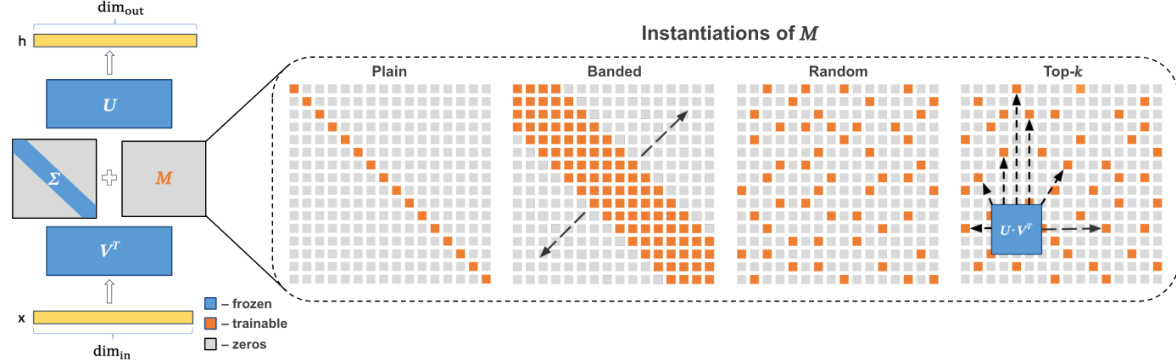
This figure illustrates the core idea of the SVFT method. The original weight matrix W is decomposed using Singular Value Decomposition (SVD) into three components: U (left singular vectors), Σ (singular values), and V (right singular vectors). SVFT introduces a sparse, learnable matrix M to modify the singular values. The figure shows four different configurations for the sparsity pattern of M: Plain (diagonal), Banded, Random, and Top-k. The orange cells represent the trainable parameters within M, while gray cells are fixed to zero. The Top-k configuration highlights a matrix where only the top k strongest interactions are trainable.

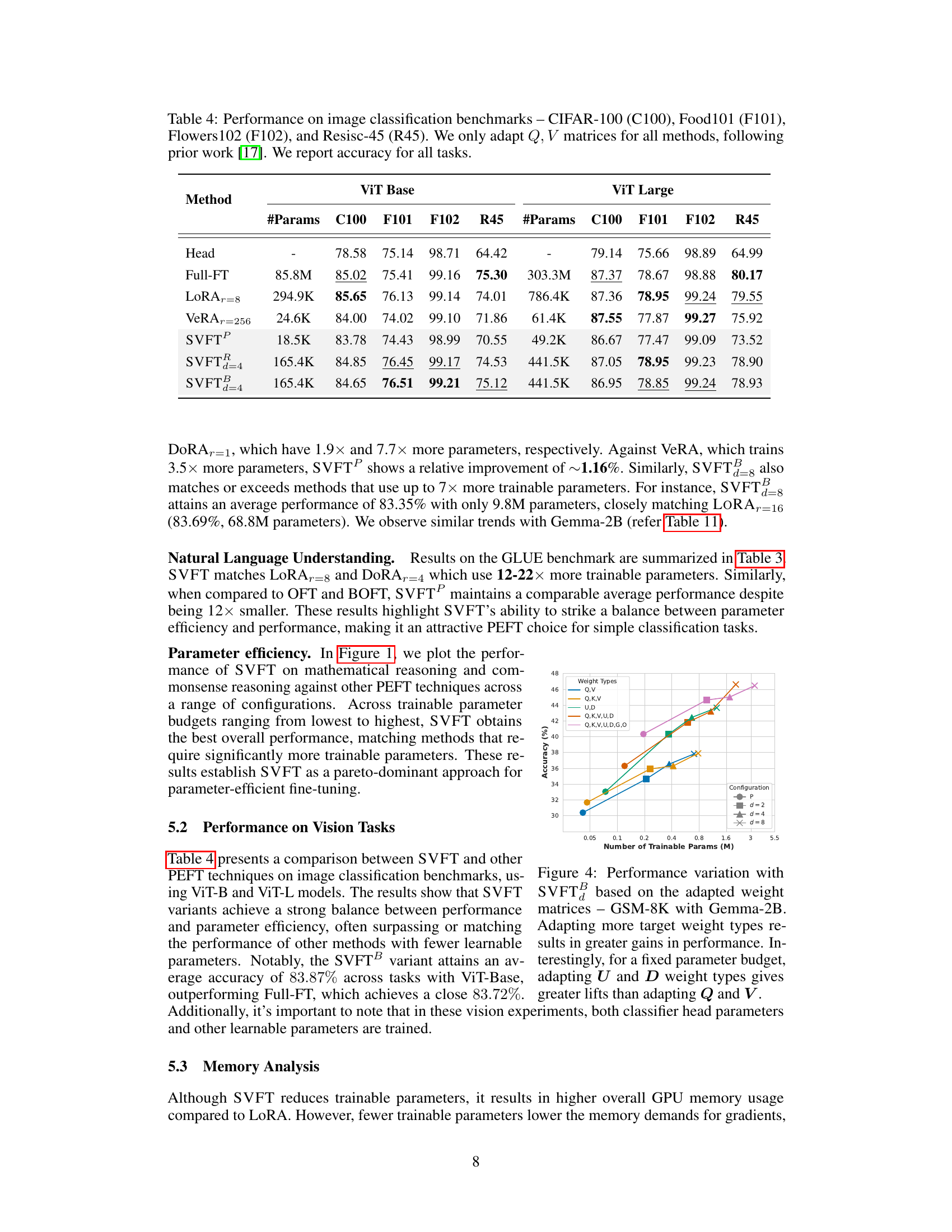
This figure shows the impact of adapting different weight matrices (Q, K, V, U, D, O, G) on the performance of SVFT. It demonstrates that including more weight types in the fine-tuning process generally leads to better accuracy. Different levels of off-diagonal elements (d = 2, 4, 8) are tested. Interestingly, it also highlights that updating the U and D weight matrices provides better performance gains compared to Q and V matrices, especially considering the same parameter budget.
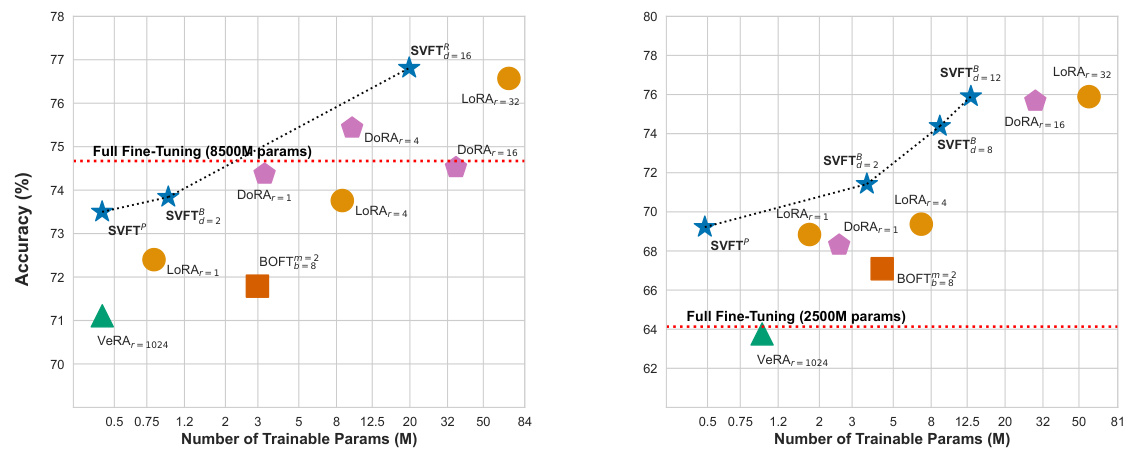
This figure compares the performance (accuracy) of various parameter-efficient fine-tuning (PEFT) methods against the number of trainable parameters used. The left panel shows results for the GSM-8K benchmark, while the right panel shows results for Commonsense Reasoning, both using the Gemma-2B language model. The figure demonstrates that SVFT consistently achieves higher accuracy than competing methods (LoRA, DORA, BOFT, VeRA) while using significantly fewer trainable parameters. Specifically, SVFT outperforms DoRA with 8 and 16 ranks while using 75% fewer parameters.
More on tables
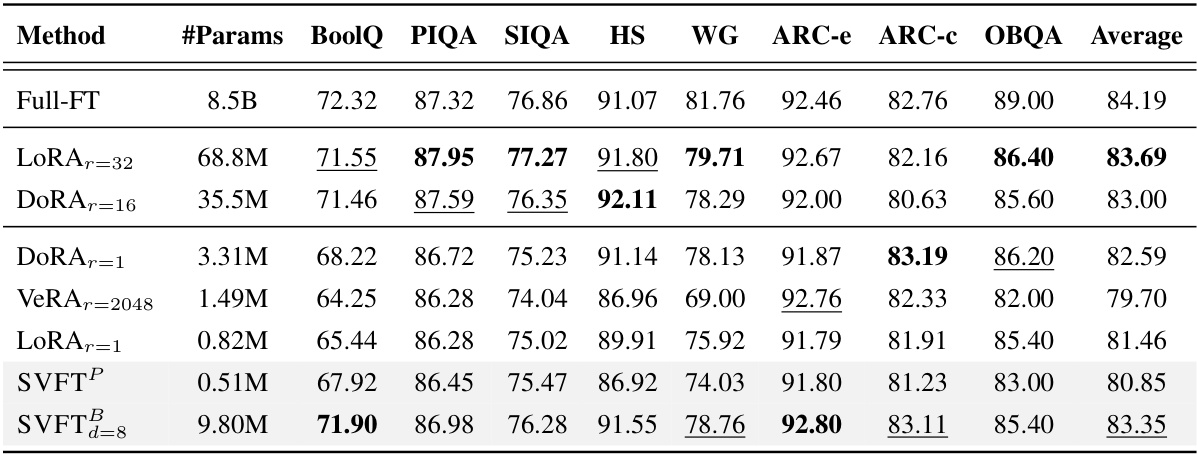
This table presents the performance comparison of different parameter-efficient fine-tuning (PEFT) methods on eight commonsense reasoning benchmarks using the Gemma-7B language model. It shows accuracy scores for each benchmark and highlights that SVFT (particularly SVFT with plain sparsity pattern) achieves competitive performance while using significantly fewer trainable parameters than other methods like LoRA and DORA.

This table presents the performance of different parameter-efficient fine-tuning (PEFT) methods, including SVFT, on the GLUE benchmark using the DeBERTaV3base model. The results show accuracy scores for various tasks within the benchmark, highlighting SVFT’s performance compared to other techniques like LoRA, DORA, and BOFT. The table provides a quantitative assessment of the different models’ effectiveness in adapting to downstream tasks, focusing on the tradeoff between parameter efficiency and accuracy.

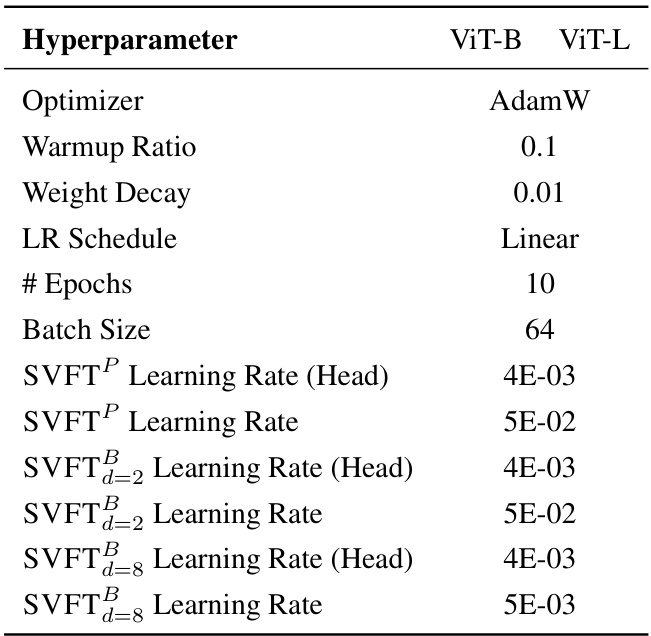
This table presents the performance of different parameter-efficient fine-tuning (PEFT) methods on image classification tasks using two different vision transformer models (ViT Base and ViT Large). The accuracy of each method is reported for four different benchmark datasets (CIFAR-100, Food101, Flowers102, and Resisc-45). Only the Q and V matrices in each model are fine-tuned for the experiments. The results show the accuracy achieved for each method, the number of trainable parameters used, and the model variant used (ViT Base or ViT Large).
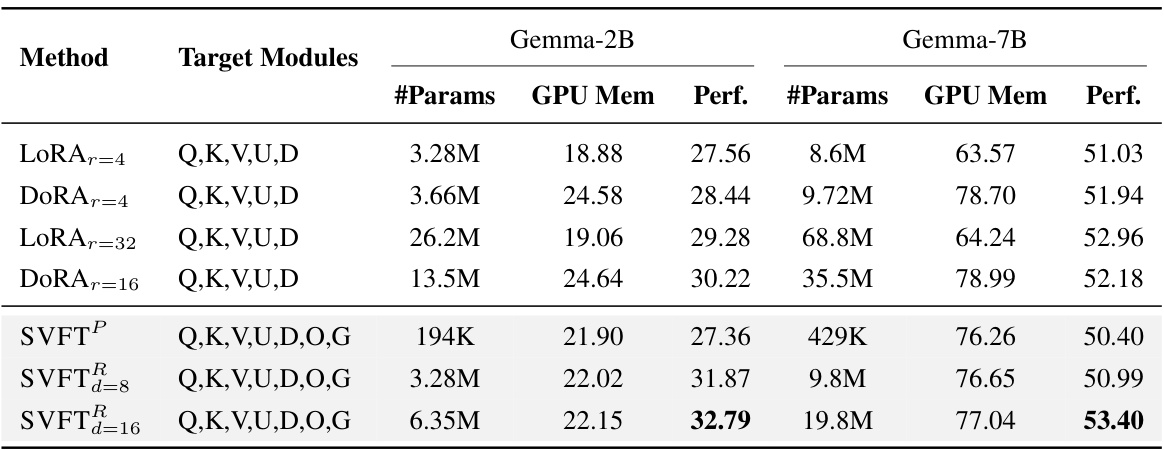
This table compares the GPU memory usage and performance of different parameter-efficient fine-tuning (PEFT) methods, including LoRA, DoRA, and SVFT variants, on the GSM-8K and MATH benchmarks using Gemma-2B and Gemma-7B language models. It demonstrates that SVFT achieves comparable or better performance than LoRA and DoRA while using less GPU memory than DoRA.

This table shows the performance improvement (ΔPerf) achieved by fine-tuning three different methods (Full-FT, LoRA, and SVFT) on the GSM-8K benchmark using Pythia-2.8B checkpoints at two different pre-training stages (39K and 143K steps). The table displays the number of parameters (#Params) used by each method and their respective performance gains. The results demonstrate that SVFT shows a greater improvement with better pre-trained weights and that SVFT outperforms LoRA in both settings.
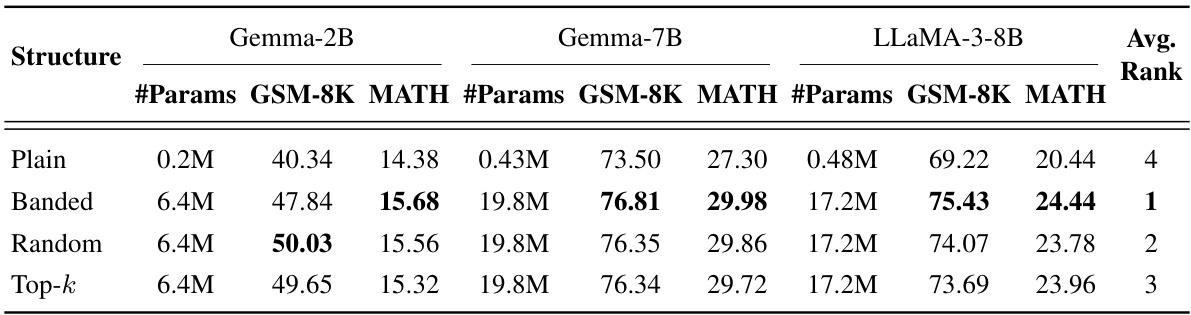
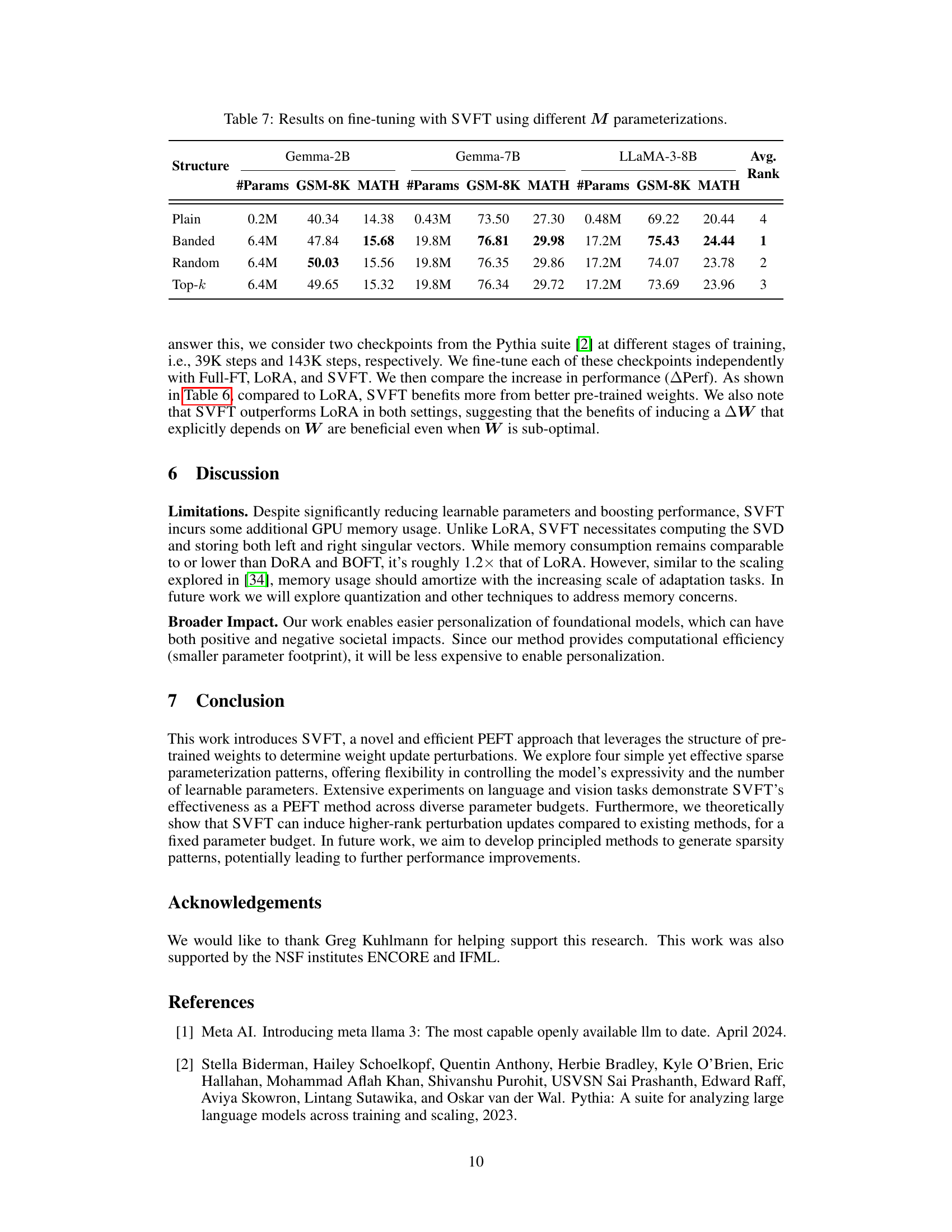
This table presents the results of fine-tuning experiments using the Singular Vectors guided Fine-Tuning (SVFT) method with four different sparsity patterns for the trainable matrix M: Plain, Banded, Random, and Top-k. The table shows the number of parameters used, and the performance (accuracy) on the GSM-8K and MATH benchmarks for three different language models: Gemma-2B, Gemma-7B, and LLaMA-3-8B. The average rank achieved by each sparsity pattern across the three models is also provided. This allows for a comparison of performance and parameter efficiency for the different sparsity patterns.

This table compares the number of trainable parameters for different parameter-efficient fine-tuning (PEFT) methods. It shows the formulas for calculating the number of trainable parameters for LoRA, DoRA, VeRA, and two variants of SVFT (SVFTP and SVFTB). The formulas take into account the number of layers being adapted (Ltuned), the model dimension (Dmodel), the rank (r), and the number of additional off-diagonal elements (k). This provides a quantitative comparison of the parameter efficiency of different PEFT methods.

This table compares the performance of SVF and SVFT on the GSM-8K and MATH benchmarks using the Gemma-2B model. It shows that SVFT, especially with off-diagonal elements, outperforms SVF. The results highlight the advantage of learning the off-diagonal elements in SVFT for improved performance.
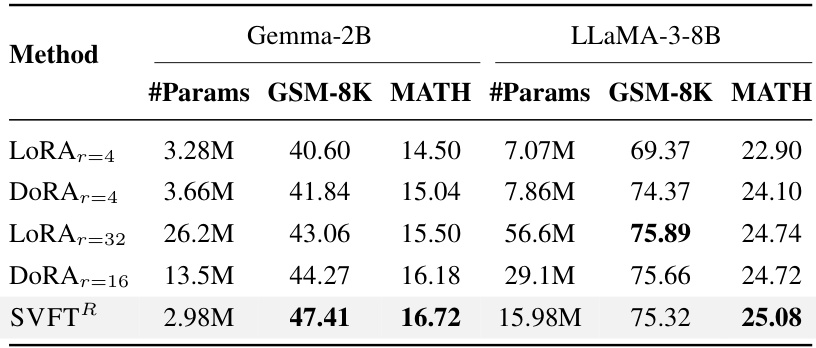
This table presents the accuracy results on GSM-8K and MATH benchmark datasets for different parameter-efficient fine-tuning (PEFT) methods. The methods are compared based on their performance, measured by accuracy, and the number of trainable parameters used. The target modules (Q, K, V, U, D) are the same across all methods, allowing for a fairer comparison. The table shows that SVFT achieves better accuracy than other methods with similar or fewer parameters.
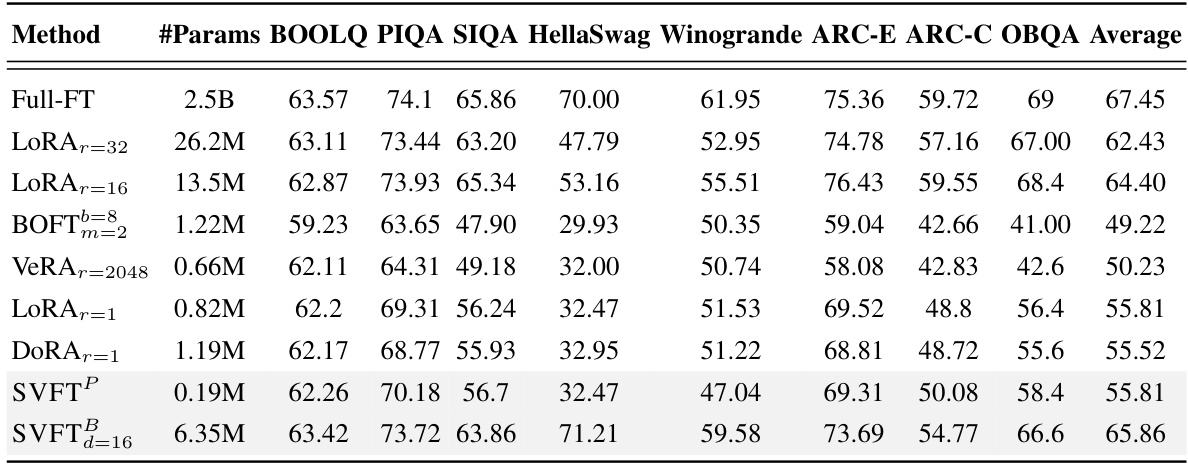
This table presents the performance of various parameter-efficient fine-tuning (PEFT) methods on eight commonsense reasoning benchmarks using the Gemma-7B language model. It compares the accuracy achieved by Full Fine-Tuning (Full-FT), LoRA (with different ranks), DoRA (with different ranks), BOFT, VeRA, and SVFT (both plain and banded versions) across the benchmarks. The table highlights SVFT’s competitive performance while using significantly fewer trainable parameters than other methods.

This table presents the performance of SVFT on GSM-8K and MATH datasets with different rank (r) and number of off-diagonal elements (d) in the trainable matrix M. It shows how performance changes as the model’s expressivity and the number of trainable parameters are varied. The full-rank model (r=2048) achieves the best performance, highlighting the importance of considering all singular vectors and values during fine-tuning.

This table compares the GPU memory usage and performance (measured by accuracy on GSM-8K and MATH datasets) of different parameter-efficient fine-tuning (PEFT) methods. The methods compared are LoRA, DoRA, and SVFT with varying numbers of parameters. The results show that SVFT achieves comparable or better performance while using less GPU memory than DoRA, although using slightly more memory than LoRA.
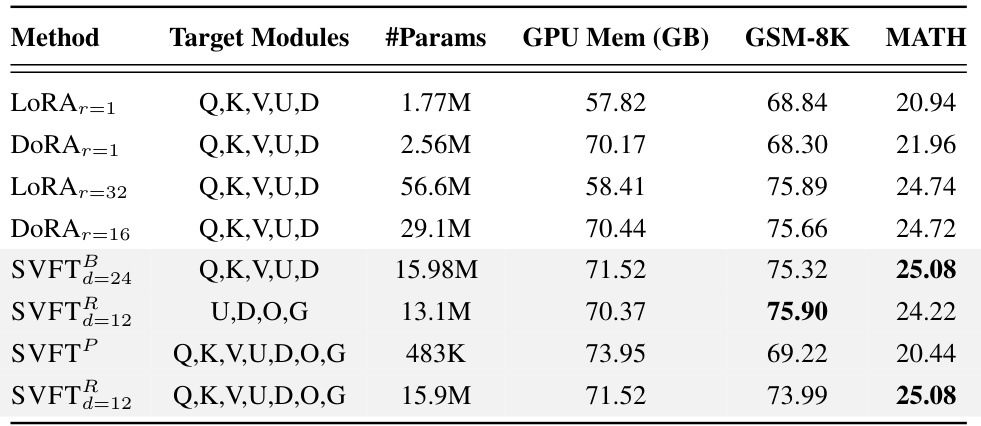
This table presents the GPU memory usage (in GB) and performance (accuracy) on GSM-8K and MATH benchmarks for different parameter-efficient fine-tuning (PEFT) methods, including LoRA, DoRA, and SVFT variants. The table shows the number of parameters (#Params) used by each method and the corresponding GPU memory consumption. It provides a comparison of memory efficiency and performance across various PEFT techniques, highlighting the trade-off between model size and accuracy. The target modules adapted are also specified for each method.

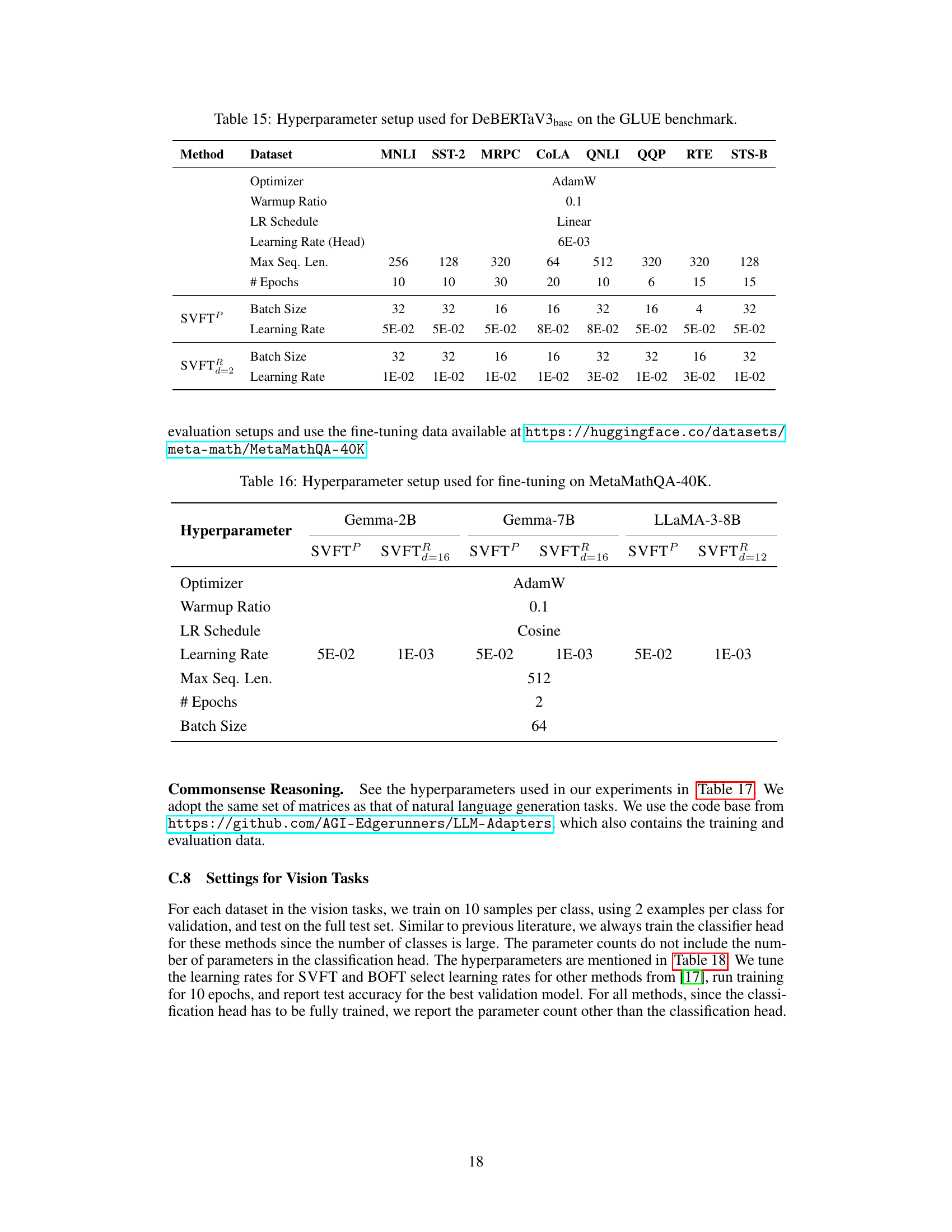
This table shows the hyperparameter settings used for fine-tuning the DeBERTaV3base model on the GLUE benchmark. It includes details for both SVFTP and SVFT2 (with d=2), specifying the optimizer (AdamW), warmup ratio (0.1), learning rate schedule (linear), learning rates (for the head and the main model), maximum sequence length, number of epochs, and batch size for each task within the GLUE benchmark (MNLI, SST-2, MRPC, CoLA, QNLI, QQP, RTE, STS-B). The table provides a detailed configuration of the hyperparameters used in the experiments described in the paper, facilitating reproducibility and comparison.
This table compares the performance of SVFT against other parameter-efficient fine-tuning (PEFT) methods and full fine-tuning on two mathematical reasoning benchmarks: GSM-8K and MATH. The results are presented in terms of accuracy and the number of trainable parameters used by each method. The table highlights that SVFT achieves either the best or second-best accuracy while using significantly fewer parameters than the other methods.
This table shows the hyperparameter settings used for fine-tuning on the commonsense-15K dataset. It lists the hyperparameters for different models (Gemma-2B and Gemma-7B) and variations of the SVFT method (SVFTP and SVFTBd=8). The hyperparameters include the optimizer, warmup steps, learning rate schedule, maximum sequence length, number of epochs, batch size, and the learning rate itself. These settings are crucial for reproducibility of the experiments in this section of the paper.
This table presents the performance (accuracy) of different parameter-efficient fine-tuning (PEFT) methods and full fine-tuning on two mathematical reasoning benchmarks: GSM-8K and MATH. It compares the accuracy achieved by various methods (Full-FT, LoRA, DoRA, BOFT, VeRA, and SVFT) while considering the number of trainable parameters used. The table highlights SVFT’s superior or competitive performance with significantly fewer trainable parameters compared to other methods. The hyperparameter ’d’ used in SVFT is specified for different base models.
Full paper#