TL;DR#
Many machine learning models unintentionally exhibit biases against certain demographic groups, violating fairness. Existing fairness methods often require access to sensitive attributes (like race or gender), but this is problematic for privacy and data availability reasons. This paper focuses on regression tasks—predicting a continuous value like income—and tackles the challenge of ensuring fair predictions without using this sensitive information during the prediction phase.
This research introduces a novel post-processing algorithm that addresses these issues. It uses accurate estimates of the regression function and sensitive attribute predictor to generate predictions satisfying the demographic parity constraint. The method leverages discretization and stochastic optimization of a smooth convex function, making it suitable for online post-processing. The algorithm boasts strong theoretical guarantees, including finite-sample analysis and post-processing bounds, which are validated through experiments.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on algorithmic fairness, especially those focusing on regression tasks and unsupervised post-processing. It offers a novel, theoretically-grounded method for achieving demographic parity even without access to sensitive attributes during inference. The provided algorithm is computationally efficient and backed by strong theoretical guarantees, opening new avenues for research in fair machine learning.
Visual Insights#

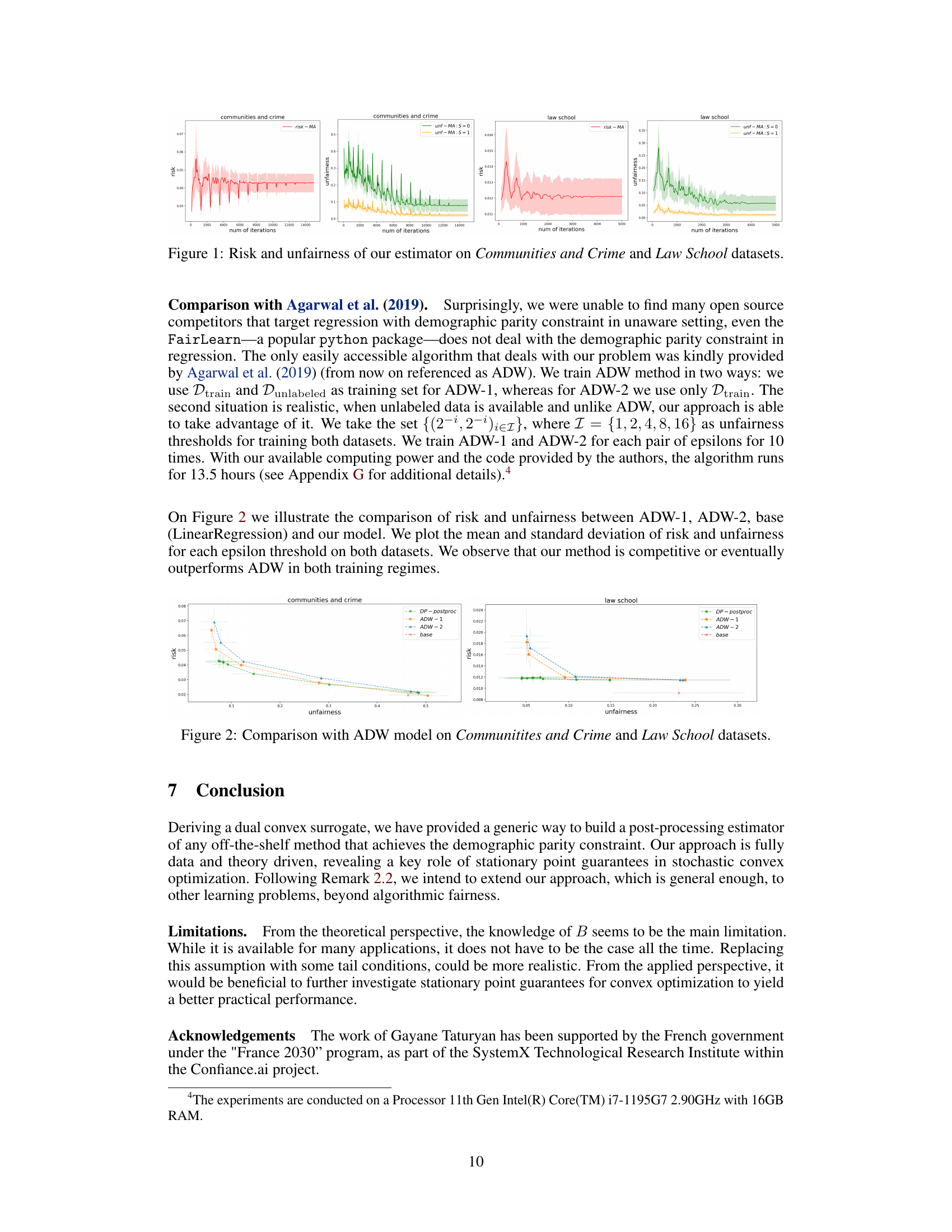
🔼 This figure displays the convergence of the risk and unfairness of the proposed demographic parity constrained regression algorithm over iterations for the Communities and Crime dataset and the Law School dataset. The plots show how the risk (mean squared error) and the unfairness (measured by the maximum difference in conditional outcome distributions across sensitive groups) change as the algorithm progresses. The shaded area represents the standard deviation across multiple runs.
read the caption
Figure 1: Risk and unfairness of our estimator on Communities and Crime and Law School datasets.

🔼 This table shows the average training time in seconds for one epsilon threshold. The training times are presented for three datasets: Communities and Crime, Law School, and Adult. For each dataset, the average training time is reported for three methods: DP-postproc (the proposed method), ADW-1 (Agarwal et al. method trained with both labeled and unlabeled data), and ADW-2 (Agarwal et al. method trained only with labeled data). The table provides a comparison of the computational efficiency of the proposed method relative to the existing method.
read the caption
Table 1: The average training time (in seconds) for one ɛ threshold.
In-depth insights#
Fair Regression’s Challenge#
Fair regression presents a significant challenge in machine learning due to the inherent conflict between accuracy and fairness. Standard regression techniques aim to minimize prediction error, often ignoring potential biases embedded within the training data. These biases can lead to discriminatory outcomes, particularly affecting sensitive groups. Achieving fair regression necessitates methods that simultaneously minimize prediction error while mitigating bias, a problem complicated by the lack of universally agreed-upon definitions of fairness. Different fairness notions (e.g., demographic parity, equalized odds) lead to different optimization objectives, making the choice of appropriate metric crucial and context-dependent. The difficulty is further compounded by the scarcity of labeled data for sensitive attributes, limiting the ability to directly enforce fairness constraints. Therefore, developing effective fair regression algorithms necessitates innovative approaches that handle data scarcity, balance competing objectives, and allow for flexible fairness criteria tailored to specific application contexts. Theoretical guarantees are also vital for ensuring the reliability and robustness of fair regression models. Successfully addressing the challenge requires a multi-faceted approach combining algorithmic innovations with careful consideration of ethical implications and societal impact.
Unlabeled Post-Processing#
Unlabeled post-processing addresses a crucial challenge in fair machine learning: achieving demographic parity in regression tasks without access to sensitive attributes during the prediction phase. This constraint makes it impossible to directly adjust predictions based on sensitive characteristics. The core idea is to leverage accurate estimates of the regression function and a sensitive attribute predictor (obtained from a separate labeled dataset) to generate predictions that satisfy demographic parity constraints on unlabeled data. This approach is particularly valuable when sensitive attribute information is unavailable or ethically problematic to use at prediction time. The algorithm combines discretization, stochastic optimization of a smooth convex function, and advanced gradient-control techniques to guarantee both fairness and accuracy, which are backed by theoretical guarantees. Unlike previous methods that lack rigorous theoretical analysis, this method provides finite-sample analysis and post-processing bounds, making it a significant contribution to the field of fair machine learning. The reliance on unlabeled data significantly broadens the applicability of this approach.
Convex Optimization’s Role#
The paper leverages convex optimization to address the challenge of achieving demographic parity in regression tasks, particularly in the challenging scenario of unawareness (sensitive attributes unavailable during inference). A smooth convex objective function is designed, whose minimization yields predictions satisfying the demographic parity constraint. This approach is fully theory-driven, offering precise control over the gradient norm to ensure both fairness and accuracy guarantees, unlike previous methods. The chosen objective function is well-suited for online post-processing, handling streaming unlabeled data efficiently. Entropic regularization is incorporated, managing the trade-off between fairness and risk. Stochastic optimization techniques are employed, enabling scalability and efficiency. The framework’s strength lies in its theoretical foundations, underpinning its practical advantages for fairness-aware regression in real-world applications.
Discretization & Regularization#
The core idea is to discretize the prediction space, transforming the continuous regression problem into a finite-dimensional one, making it easier to handle computationally. This discretization introduces a trade-off: a finer grid (more discretization points) improves accuracy but increases computational complexity and the number of fairness constraints to satisfy. To manage this complexity and mitigate potential issues from the discretization, the authors introduce entropic regularization. This regularization technique helps to smooth the objective function, promoting better numerical stability during optimization and potentially improving the generalization performance of the learned model by preventing overfitting to the discretized space. The combination of discretization and entropic regularization offers a practical and theoretically sound way to address the challenging problem of regression under fairness constraints in the unawareness setting.
Empirical Validation & Limits#
An ‘Empirical Validation & Limits’ section would critically assess the proposed fairness-aware regression algorithm. It would begin by describing the experimental setup, including datasets used (ideally diverse to show generalizability), evaluation metrics (e.g., risk, fairness measures), and baseline methods for comparison. Key results would demonstrate the algorithm’s effectiveness in achieving demographic parity while maintaining competitive predictive accuracy, showing statistical significance. The section would then delve into the algorithm’s limitations. This could include scenarios where performance degrades (e.g., high dimensionality, imbalanced datasets), sensitivity to hyperparameter choices, and computational costs. A discussion of the algorithm’s robustness to violations of underlying assumptions is vital. For instance, how does the algorithm perform when the sensitive attribute is not perfectly predicted or when the data exhibits correlation structures not accounted for in the theoretical analysis? Finally, it is important to provide concrete examples illustrating these limitations, perhaps with visualizations. The section should conclude by summarizing the algorithm’s strengths and weaknesses, highlighting areas for future work. This might involve developing more robust estimation techniques, exploring different fairness definitions, or designing more efficient algorithms.
More visual insights#
More on figures
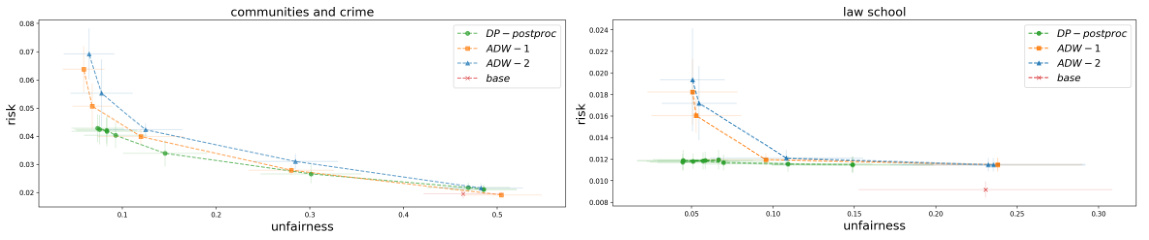
🔼 This figure compares the performance of the proposed DP-postproc algorithm with the ADW algorithm (Agarwal et al., 2019) and a simple base regression model on two datasets: Communities and Crime, and Law School. The comparison is done in terms of risk and unfairness, across a range of unfairness thresholds. Both ADW versions (ADW-1 using both labelled and unlabelled data, ADW-2 using only labelled data) are included. The plot shows that DP-postproc is competitive or outperforms ADW across various settings.
read the caption
Figure 2: Comparison with ADW model on Communitites and Crime and Law School datasets.

🔼 This figure compares the performance of several stochastic gradient descent algorithms (SDG, ACSA, ACSA2, SDG3+ACSA, SDG3+ACSA2) on two benchmark datasets: Communities and Crime, and Law School. The algorithms are evaluated across a range of unfairness levels, with the x-axis representing unfairness and the y-axis showing the risk. The plot illustrates how different algorithms behave under varying levels of fairness constraints, highlighting their strengths and weaknesses in achieving a balance between fairness and accuracy.
read the caption
Figure 3: Comparison of SDG, ACSA, ACSA2, SDG3+ACSA and SDG3+ACSA2 algorithms on Communities and Crime and Law School datasets.
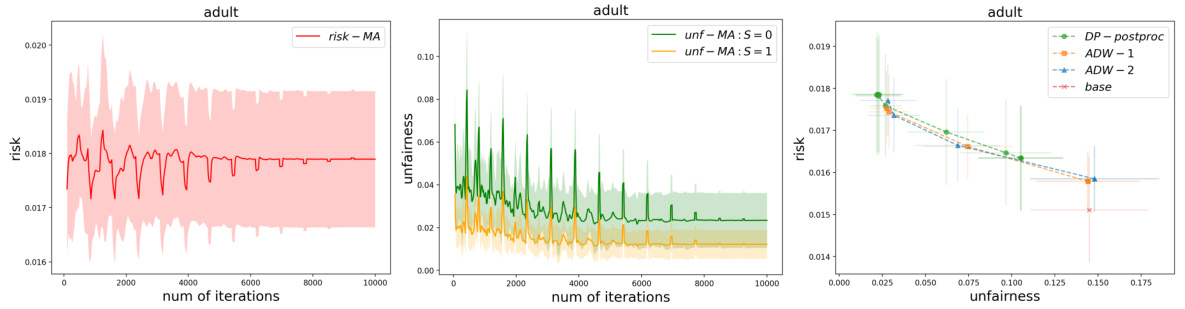
🔼 This figure displays the results of the experiment conducted on the Adult dataset. It shows the convergence of risk and unfairness for the proposed DP-postprocessing method and compares its performance to the ADW method (with and without unlabeled data) and the base model. The convergence is shown for an unfairness threshold of ε = (2⁻⁸, 2⁻⁸).
read the caption
Figure 4: Experiment on Adult dataset: risk convergence, unfairness convergence and comparison with ADW.
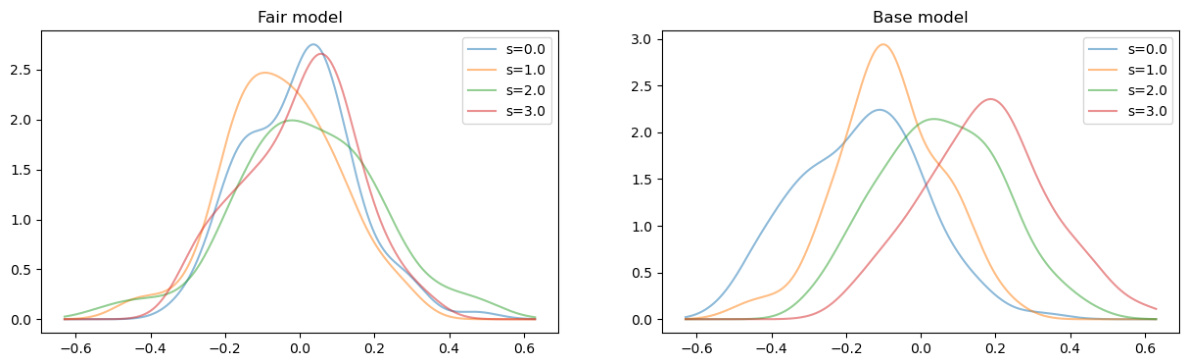
🔼 This figure displays the distributions of predictions from both the fair model (left panel) and the base model (right panel), categorized by the values of sensitive attribute S. The x-axis represents the scaled predictions, and the y-axis represents the density. The purpose is to visually demonstrate the impact of the proposed fair post-processing method. The comparison highlights how the fair model’s predictions are more evenly distributed across different groups (defined by S), reducing bias compared to the base model.
read the caption
Figure 5: The distributions of the (scaled) predictions of the fair and base models.
Full paper#