TL;DR#
Gradual domain adaptation is challenging because of the high cost of continuously labeling datasets for training machine learning models. Existing methods often lead to exponentially increasing errors as the model adapts to successive datasets. This paper tackles this problem by considering data distributions exhibiting a known favorable attribute (e.g., intra-class soft/hard margins). It introduces a sequence of data distributions with gradual shifts, where consecutive distributions are close in Wasserstein distance.
The paper proposes a novel methodology rooted in Distributionally Robust Optimization (DRO) with an adaptive Wasserstein radius. It introduces a “compatibility measure” that characterizes error propagation dynamics along the sequence. This measure demonstrates that, for appropriately constrained distributions, error propagation can be bounded and potentially eradicated. This is substantiated by theoretical bounds and experimental results on Gaussian generative models and more general “expandable” distributions.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working in domain adaptation, particularly those tackling gradual domain shifts. It offers novel theoretical guarantees and practical methodologies for handling such scenarios, potentially improving the robustness and reliability of machine learning models across various applications.
Visual Insights#

🔼 This figure illustrates the workings of the manifold-constrained DRO method for gradual domain adaptation. It shows how a restricted adversarial block (fp) perturbs the source distribution at each step to prepare for the worst-case scenario in the next step. Simultaneously, a classifier (fc) learns from this perturbed distribution. This process aims to improve the robustness and adaptability of the classifier across gradually shifting domains.
read the caption
Figure 1: A schematic view of the proposed procedure for our manifold-constrained DRO. A restricted adversarial block, modeled by fp, tries to perturb the source distribution at each step i to prepare the algorithm for the worst possible distribution in step i + 1. Meanwhile, a classifier fc tries to learn a classifier based on the perturbed distribution.
In-depth insights#
DRO in GDA#
The application of Distributionally Robust Optimization (DRO) to Gradual Domain Adaptation (GDA) presents a promising approach to address the challenges of adapting machine learning models to sequentially shifting data distributions. DRO’s inherent robustness against distributional uncertainty is particularly well-suited to the GDA setting, where the precise characteristics of future data distributions are unknown. By formulating the GDA problem as a DRO problem, the method seeks to find models that perform well not just on the current data distribution, but also on a set of plausible future distributions. This robustness is crucial for mitigating the risk of performance degradation as the data distribution evolves. A key challenge in this approach lies in defining a suitable uncertainty set—the set of plausible distributions considered by the DRO formulation. A poorly chosen uncertainty set can lead to overly conservative or ineffective models. The paper’s contributions in this area are valuable, as they introduce new techniques for adaptively choosing the uncertainty set based on observed data. This adaptive approach allows the DRO formulation to progressively refine its estimate of future data distributions as more information becomes available. The theoretical analysis that establishes error bounds under the proposed method is noteworthy. This provides valuable insights into the conditions under which DRO can effectively control error propagation, and guides the choices of key parameters for optimal performance. However, the practical applicability of the proposed method hinges on its computational efficiency. DRO problems can be computationally intensive, particularly with large datasets or complex models. Therefore, further research in this area is warranted to assess the scalability and performance of the proposed techniques in real-world applications.
Manifold Impact#
The concept of ‘Manifold Impact’ in a research paper likely refers to how the underlying data manifold structure influences the results. A manifold is a high-dimensional space that can be locally represented in a lower dimension. In machine learning, data often lies on or near a low-dimensional manifold embedded in a high-dimensional space. The manifold’s curvature, intrinsic dimensionality, and density variations directly impact the performance of machine learning models. A model’s ability to capture the manifold’s geometry determines its generalization capabilities. For instance, a model trained on a highly curved manifold may struggle to generalize to unseen data points on the same manifold, unlike a model trained on a flat manifold. Algorithms that explicitly leverage the manifold structure, such as those using manifold regularization or metric learning, often show improved performance. Similarly, distributionally robust optimization (DRO) techniques often handle the uncertainties arising from data points near the boundary of the manifold or its low-density regions. Therefore, exploring the manifold impact requires analyzing data distribution, model selection, and algorithm design. A thoughtful analysis must reveal how manifold properties affect the model’s training and performance and explore strategies to mitigate potential issues. This might involve methods that adapt the model to the manifold’s curvature, deal with sparsely sampled areas, or incorporate robustness measures to handle manifold boundary effects.
Error Propagation#
The concept of ’error propagation’ is central to the research paper, focusing on how errors accumulate as a model adapts sequentially to new domains in gradual domain adaptation. The paper demonstrates that unconstrained distributions can lead to exponential error growth, making the adaptation process unstable. Conversely, the use of manifold-constrained distributionally robust optimization (DRO) is proposed as a method to mitigate this issue. By constraining the distributions to a manifold with favorable properties (e.g., hard/soft margins), the error propagation is controlled. A key contribution is the introduction of a compatibility measure which fully characterizes this error propagation behavior. This measure helps identify when the error remains bounded or escalates. The theoretical analysis is supported by experimental results validating the effectiveness of the DRO approach in limiting error escalation. The interplay between distributional constraints and the classifier hypothesis set is crucial for controlling error growth, illustrating a critical trade-off in designing effective gradual domain adaptation strategies.
Gaussian Analysis#
A Gaussian analysis in a research paper on gradual domain adaptation would likely involve using the properties of Gaussian distributions to model the data across different domains. This approach is attractive because Gaussian distributions are well-understood and have many convenient mathematical properties. The analysis might focus on the behavior of the Gaussian parameters (mean and covariance) across domains, investigating how they change as the domain shifts gradually. The goal would be to quantify the degree of similarity or divergence between the Gaussian distributions, perhaps using metrics such as the Kullback-Leibler divergence or Wasserstein distance. Such analysis would help understand the challenge of gradual domain adaptation and design algorithms to effectively transfer knowledge from one domain to another while considering the statistical characteristics of the data. The analysis may explore error bounds and generalization properties based on the Gaussian assumptions, establishing how these metrics are related to the performance of classification models in this setting. Furthermore, the analysis could investigate the impact of various constraints on the Gaussian distributions, such as constraints on the covariance matrices or assumptions of specific types of correlation between features. This in-depth analysis will likely provide valuable theoretical insights into gradual domain adaptation and guide the design of robust algorithms that adapt well to progressively changing data distributions.
Future Works#
Future research directions stemming from this gradual domain adaptation work could involve exploring alternative DRO formulations beyond Wasserstein distance, potentially using other divergence measures like f-divergences. Another promising avenue lies in investigating the impact of different manifold constraints on error propagation and exploring more general manifold learning techniques. The current method assumes a known favorable attribute; relaxing this assumption to handle more complex data distributions poses a significant challenge. Additionally, extending the approach to handle more than two classes, to multi-class problems, would broaden its applicability. Finally, exploring the practical implications and scalability of the algorithm on very large datasets would be crucial for real-world applications.
More visual insights#
More on figures
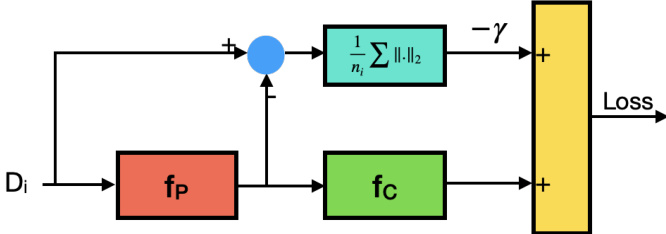
🔼 The figure shows a schematic representation of the proposed manifold-constrained DRO method for gradual domain adaptation. The input data (Di) first passes through a perturbation function (fp), which adds controlled noise. This perturbed data is then fed to a classifier (fc), and the output is combined with the original labels (-γ) to calculate a loss. The method aims to find a robust classifier by iteratively perturbing data and training the classifier.
read the caption
Figure 1: A schematic view of the proposed procedure for our manifold-constrained DRO. A restricted adversarial block, modeled by fp, tries to perturb the source distribution at each step i to prepare the algorithm for the worst possible distribution in step i + 1. Meanwhile, a classifier fc tries to learn a classifier based on the perturbed distribution.
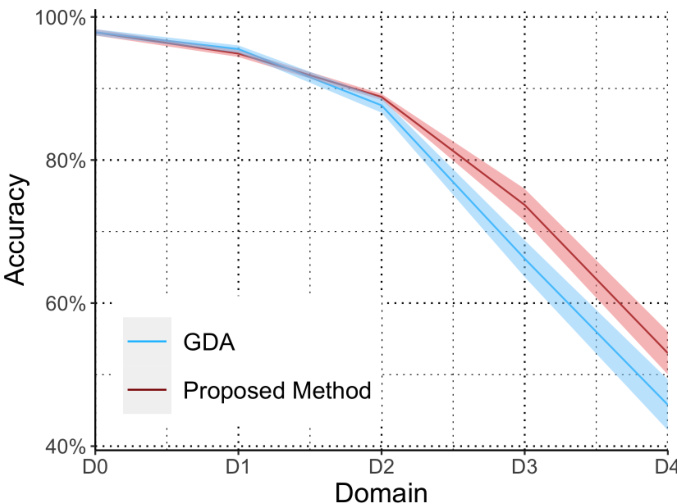
🔼 The figure compares the performance of the proposed gradual domain adaptation method with the GDA method [KML20] on the rotating MNIST dataset. The x-axis represents the different domains (D0 to D4), where each domain corresponds to a different rotation angle of the MNIST images. The y-axis represents the accuracy of each method on each domain. The figure shows that the proposed method consistently outperforms the GDA method across all domains, demonstrating its effectiveness in handling gradual domain shifts. The error bars suggest that this outperformance is statistically significant, although more information would be needed to confirm this statistically.
read the caption
Figure 2: Comparison of the performance of our proposed method with the GDA [KML20] on rotating MNIST dataset.
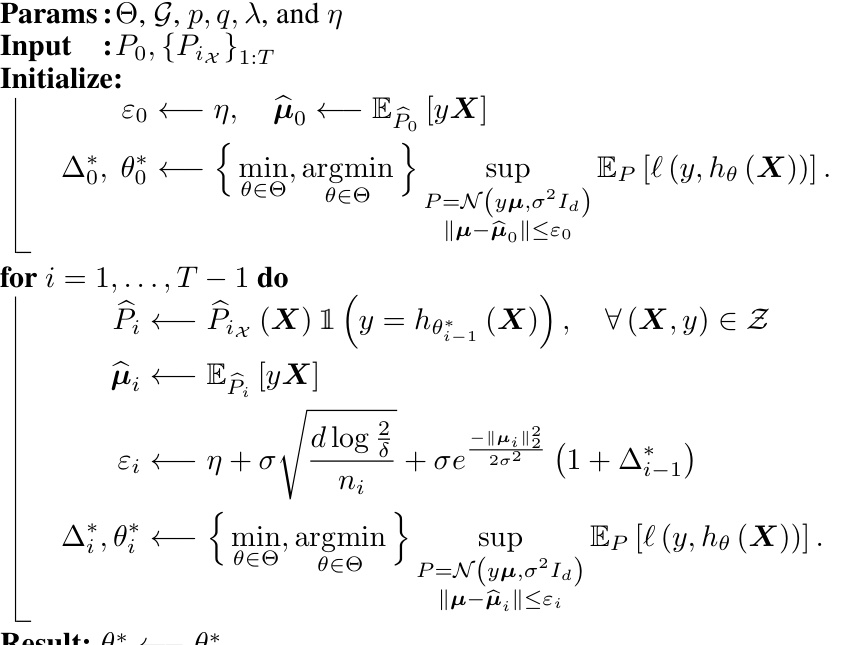
🔼 This figure shows a schematic of the manifold-constrained DRO method used in the paper. It illustrates how the method iteratively perturbs the source distribution using an adversarial block (fp) to prepare for the next distribution in the sequence. A classifier (fc) then learns from this perturbed data. This process aims to improve the robustness of the model against distribution shifts.
read the caption
Figure 1: A schematic view of the proposed procedure for our manifold-constrained DRO. A restricted adversarial block, modeled by fp, tries to perturb the source distribution at each step i to prepare the algorithm for the worst possible distribution in step i + 1. Meanwhile, a classifier fc tries to learn a classifier based on the perturbed distribution.
Full paper#



















