TL;DR#
Many large-scale simulation models are computationally expensive, hindering their use in policy-making. Existing surrogate models often fail to accurately reflect the original model’s behavior under policy interventions. This creates a critical need for more reliable surrogates that accurately reflect system behavior.
This research addresses this by introducing a framework for building interventionally consistent surrogate models using recent advances in causal abstraction. The method views both the original and surrogate models as structural causal models, focusing on preserving the model’s dynamics under various interventions. The authors demonstrate, via theoretical analysis and empirical studies, that their approach generates surrogates that mimic the original simulator’s behavior accurately under interventions of interest, allowing for rapid and reliable policy experimentation.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with complex simulation models because it offers a novel framework for creating efficient and reliable surrogate models. This is important due to the high computational cost often associated with such models, and the method presented here provides a solution for this. The causal abstraction approach presented opens up new research directions in the application of causal reasoning to surrogate modelling. The work has high potential impact, particularly for policy decision making in complex socio-technical systems where rapid experimentation and analysis are paramount.
Visual Insights#
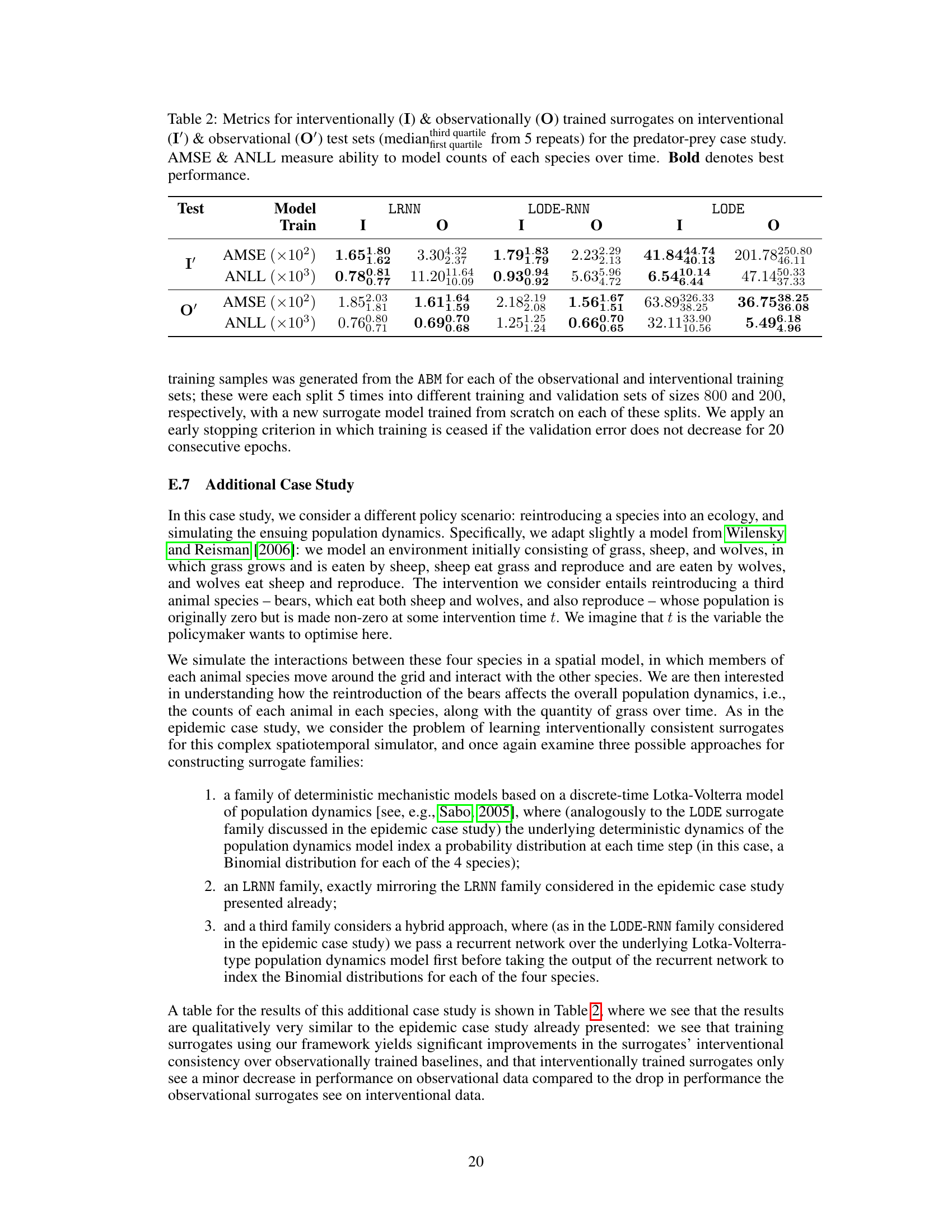
🔼 This figure shows the directed acyclic graph (DAG) representing the causal relationships between variables in a spatial SIRS (Susceptible-Infected-Recovered-Susceptible) agent-based model. The nodes represent variables, with ‘a’ representing an exogenous variable for initialization, ‘v’ representing exogenous variables for model parameters, ‘Io’ being the initial infection proportion, ‘ut’ are the exogenous random variables influencing the transition of states at each time step, ‘xt’ representing the state of the agents at each time step, and ‘θt’ representing the model parameters at each time step. The arrows indicate the direction of causal influence. The DAG visualizes the causal structure of the model, which is crucial for understanding interventions and their effects.
read the caption
Figure 1: The directed acyclic graph induced by the structural causal model for the spatial SIRS agent-based model for T = 3 time steps.

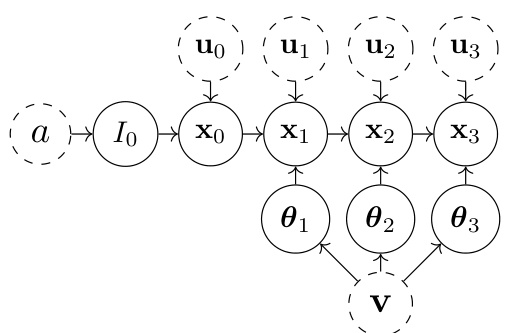
🔼 This table presents the results of the experiments evaluating the performance of interventionally and observationally trained surrogates. It compares the performance of three different surrogate models (LRNN, LODE-RNN, LODE) trained using both interventional and observational data on two test sets: an interventional test set (I’) and an observational test set (O’). The metrics used to assess performance are the average mean squared error (AMSE) and average negative log-likelihood (ANLL). The table shows that interventionally trained surrogates generally outperform observationally trained surrogates, particularly on the interventional test set.
read the caption
Table 1: Metrics for interventionally (I) & observationally (O) trained surrogates on interventional & observational (O') test sets (median, first quartile, third quartile from 5 repeats). Bold denotes best performance.
In-depth insights#
Causal Surrogates#
The concept of “Causal Surrogates” in the context of complex simulation models addresses the computational limitations of high-fidelity simulators. These surrogates aim to mimic the behavior of the original model, specifically focusing on preserving causal relationships and responses to interventions. This contrasts with traditional surrogates that simply approximate the input-output mapping, potentially neglecting crucial causal dynamics. A key advantage is the capacity for rapid experimentation with policy interventions; assessing the effects of changes without the high computational cost of running the full simulation many times. The effectiveness hinges on the surrogate model accurately capturing the causal structure; ensuring interventions have consistent impacts in both the surrogate and the original model. This requires sophisticated methods for building and validating the surrogate, often incorporating causal inference techniques. Such methods aim to learn not just correlations but underlying causal mechanisms, ensuring reliable predictions under different interventions. The accuracy and reliability of causal surrogates are paramount, and careful validation is necessary to build trust and confidence in their results for informed decision-making.
Intervention Consistency#
Intervention consistency, in the context of surrogate modeling for complex simulations, centers on ensuring that a simplified surrogate model accurately reflects the behavior of the original complex model under various interventions. This is crucial because the primary purpose of building surrogates is often to facilitate efficient experimentation with policy changes or other interventions, which would be computationally expensive with the original complex model. Therefore, inconsistent behavior undermines the surrogate’s usefulness. The challenge lies in developing techniques that can learn a surrogate that is not only accurate in predicting the original model’s outputs under normal conditions, but also maintains accuracy across a range of interventions. This requires moving beyond traditional machine learning approaches, which generally focus solely on predictive accuracy, to methods that explicitly incorporate causal reasoning and interventional analysis. The paper likely investigates methods to address this by constructing surrogate models that are consistent with the complex system under interventions, potentially using causal abstraction frameworks to ensure that the surrogate accurately mimics the impact of those interventions.
Abstraction Error#
The concept of ‘Abstraction Error’ in the context of creating surrogate models for complex simulations is crucial. It quantifies the discrepancy between the behavior of a complex simulator and its simplified surrogate, especially under various interventions. Lower abstraction error indicates higher fidelity and reliability, meaning the surrogate accurately reflects the original model’s behavior under different scenarios. The choice of a suitable distance metric (e.g., Kullback-Leibler divergence) to measure this error is important. The authors highlight the significance of minimizing this error, particularly in policy-making contexts. Minimizing abstraction error ensures the surrogate model can reliably guide decision-making, predicting the impact of interventions accurately. This is vital because a high abstraction error can lead to flawed policy recommendations, undermining the usefulness of surrogate models. The framework presented provides a rigorous approach to learn surrogates with guarantees about interventional consistency, thus limiting the abstraction error.
SIRS Case Study#
The SIRS case study section provides a practical demonstration of the proposed framework for building interventionally consistent surrogates. It leverages a spatial SIRS (Susceptible-Infected-Recovered-Susceptible) epidemiological agent-based model, a complex system where policy interventions, such as lockdowns, impact disease transmission. The study highlights the crucial difference between observationally and interventionally trained surrogates. Conventionally trained surrogates, relying solely on observational data, misjudge the effect of interventions, potentially misleading decision-makers. In contrast, the interventionally consistent surrogates, trained using the proposed framework, closely mimic the original simulator’s behaviour under various interventions. This showcases the framework’s ability to learn accurate surrogates that preserve the causal dynamics of the original model, ensuring reliable policy experimentation and decision-making. The choice of using three different surrogate model families (LODE, LODE-RNN, LRNN) further enhances the analysis, allowing for a comparison of different modelling approaches and their effectiveness in capturing interventional consistency. The results demonstrate the superiority of interventionally trained surrogates and the LODE-RNN family’s effectiveness in balancing mechanistic and data-driven modelling, paving the way for efficient and reliable policy exploration in complex systems.
Future Work#
The “Future Work” section of this research paper presents several promising avenues for extending the current work on interventionally consistent surrogates for complex simulation models. One key area is a deeper investigation into the sample complexity of abstraction learning, a crucial factor in determining the efficiency and scalability of the method. This includes exploring the impact of the interventional distribution and the nature of the statistical divergence employed on the overall abstraction error. Another important direction is to extend the theoretical framework to accommodate more diverse surrogate model families, moving beyond the currently used tractable and differentiable families. This would involve exploring alternative divergences and addressing the challenges associated with less tractable models while ensuring that the crucial property of interventional consistency is preserved. Further research could focus on leveraging causal graph knowledge, to potentially accelerate the abstraction learning process and enhance the efficiency of the method. Finally, developing practical guidelines and benchmarks for assessing interventional consistency is essential to facilitate the wider adoption and application of this methodology. This could involve developing robust metrics that account for various aspects of model performance and integrating these metrics into existing simulation modeling workflows.
More visual insights#
More on figures

🔼 This figure shows the directed acyclic graph (DAG) representing the causal relationships between variables in a spatial SIRS (Susceptible-Infected-Recovered-Susceptible) agent-based model, a common model in epidemiology. The nodes represent variables, and the edges represent causal influences. Variables include initial infection rate (I0), exogenous variables (U0, U1, U2, U3, a, v), and endogenous variables (X0, X1, X2, X3, θ1, θ2, θ3). The graph visually demonstrates how exogenous variables affect both initial conditions and subsequent temporal states, revealing the underlying causal structure of the model for T=3 time steps.
read the caption
Figure 1: The directed acyclic graph induced by the structural causal model for the spatial SIRS agent-based model for T = 3 time steps.

🔼 This figure compares the trajectories of the ABM and the LODE-RNN surrogate model under an intervention (lockdown) to illustrate the importance of interventional consistency in training surrogate models. The interventionally trained model accurately predicts the effect of the lockdown on the ABM’s behavior, while the observationally trained model significantly underestimates this effect.
read the caption
Figure 5: Example trajectories from the ABM (middle) and the LODE-RNN trained interventionally (left) and observationally (right). A lockdown is imposed at the dashed vertical line. Solid (resp. dot-dash) lines show trajectories under (resp. without) the lockdown. The transmission-inhibiting effect of the lockdown is vastly underestimated in the observationally trained surrogate, while the interventionally trained surrogate accurately predicts a reduction in disease transmission.
More on tables
🔼 This table presents the performance metrics of interventionally (I) and observationally (O) trained surrogates on both interventional (I’) and observational (O’) test sets. The metrics used are Average Mean Squared Error (AMSE) and Average Negative Log-Likelihood (ANLL). The results are presented as medians and interquartile ranges from 5 repeated experiments. Bold values indicate the best performance for each metric and test set combination.
read the caption
Table 1: Metrics for interventionally (I) & observationally (O) trained surrogates on interventional & observational (O') test sets (median third first quartile quartile from 5 repeats). Bold denotes best performance.
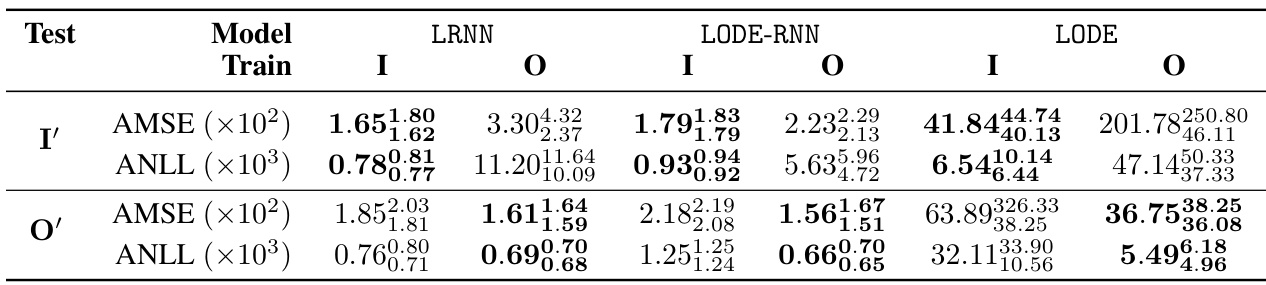
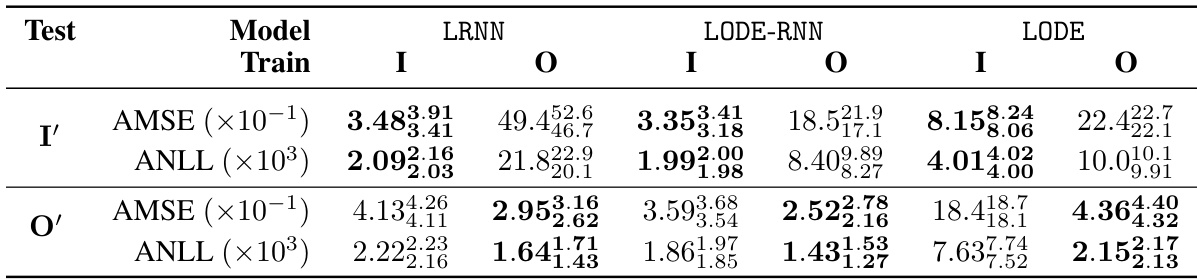
🔼 This table presents the results of an experiment comparing the performance of interventionally and observationally trained surrogates on a predator-prey model. The metrics used are the average mean squared error (AMSE) and the average negative log-likelihood (ANLL), both measuring the accuracy of the surrogate models in predicting the counts of each species over time. The table shows results for three different surrogate model families (LRNN, LODE-RNN, LODE) and two training methods (interventional and observational) across interventional and observational test sets, allowing for a comparison of the different models and training methods under different conditions.
read the caption
Table 2: Metrics for interventionally (I) & observationally (O) trained surrogates on interventional (I') & observational (O') test sets (median, first quartile, third quartile from 5 repeats) for the predator-prey case study. AMSE & ANLL measure ability to model counts of each species over time. Bold denotes best performance.
Full paper#