TL;DR#
Offline safe reinforcement learning (RL) faces challenges due to limited and potentially risky data collection. Existing methods often require unrealistic full data coverage, limiting their practical applicability. Furthermore, many methods struggle with the complexities introduced by constrained Markov decision processes (CMDPs). This paper focuses on the offline setting for convex CMDPs, a general framework that includes many practical scenarios.
The paper presents a novel primal-dual algorithm based on linear programming, incorporating ‘uncertainty’ parameters to enhance data efficiency. The algorithm is proven to achieve a sample complexity of O(1/(1-γ)√n), improving the current state-of-the-art by a factor of 1/(1-γ). This improvement is significant because it directly addresses the limitations of existing algorithms, leading to better performance in practical scenarios. The paper’s theoretical results are supported by strong empirical evidence showing improvements in both safety and learning efficiency.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in safe reinforcement learning because it addresses the critical challenge of data inefficiency and partial data coverage in offline settings. It offers a novel primal-dual method with theoretical guarantees, paving the way for more efficient and reliable safe RL algorithms. The theoretical results and experimental validation demonstrate significant improvements over existing methods, opening new avenues for real-world applications.
Visual Insights#
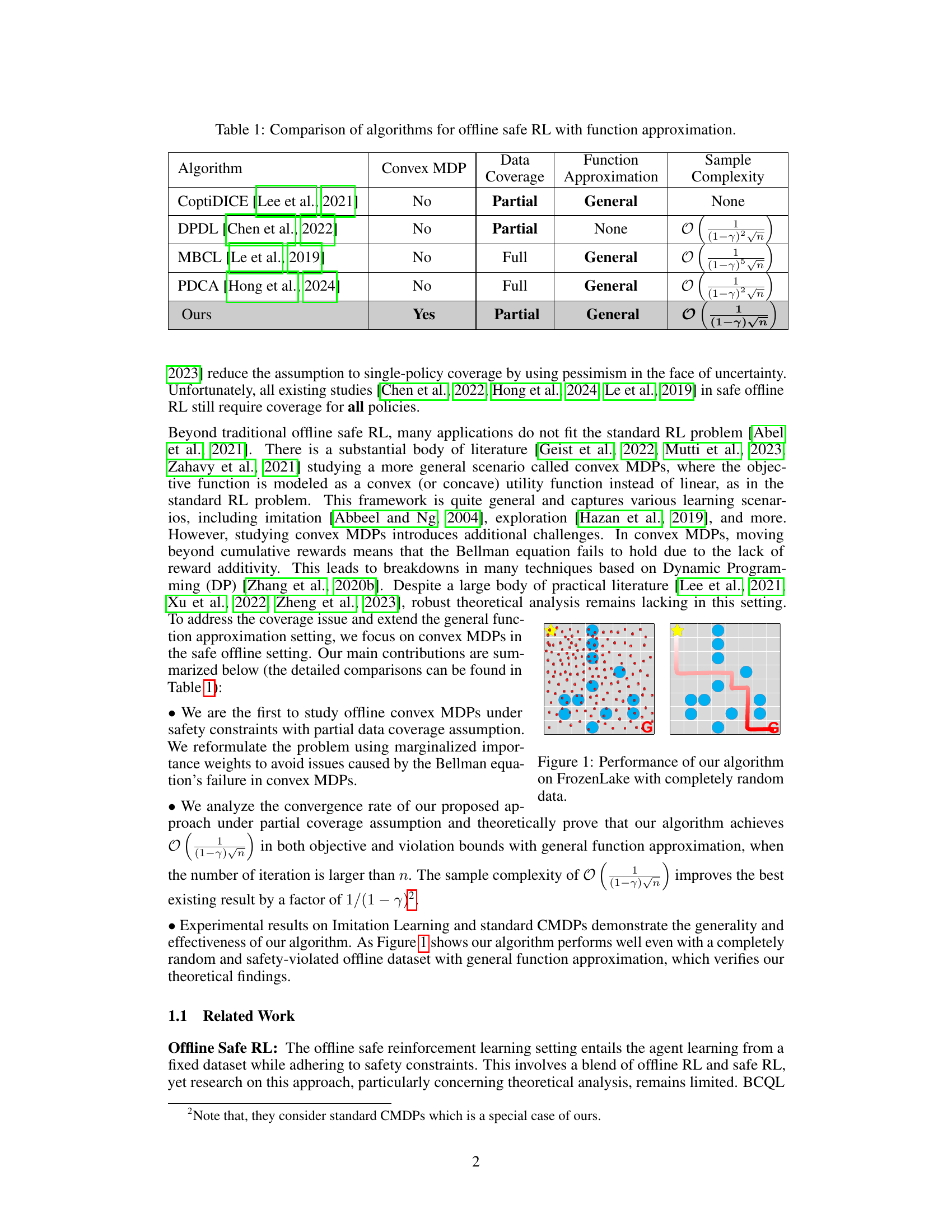
🔼 The figure shows a comparison of the agent’s performance on the FrozenLake environment when trained with completely random data using the proposed algorithm (left panel) and when trained with an ideal policy (right panel). The left panel demonstrates that even with random data, the algorithm finds a path to the goal, although it may not be optimal, whereas the right panel shows the optimal path to the goal.
read the caption
Figure 1: Performance of our algorithm on FrozenLake with completely random data.
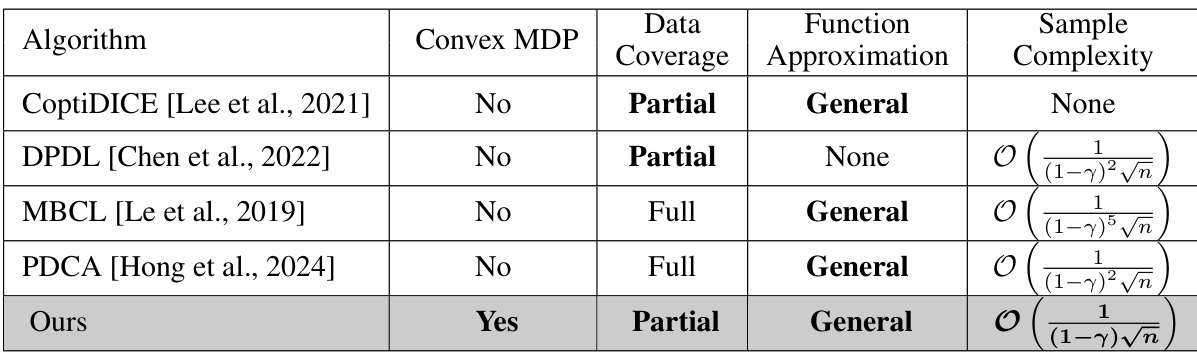
🔼 The table compares different algorithms for offline safe reinforcement learning, focusing on their assumptions regarding the type of Markov Decision Process (convex or not), data coverage (full or partial), function approximation capabilities (general or none), and sample complexity. It highlights that the proposed method improves upon existing approaches by achieving a better sample complexity under the less restrictive assumption of partial data coverage while handling convex MDPs and general function approximation.
read the caption
Table 1: Comparison of algorithms for offline safe RL with function approximation.
In-depth insights#
Primal-Dual Alg.#
A primal-dual algorithm, in the context of optimization, solves a problem by cleverly interacting between its primal and dual forms. The primal problem typically represents the original optimization goal, while the dual problem offers an alternative perspective, providing a lower bound for the primal objective. A primal-dual algorithm iteratively updates both primal and dual variables, aiming to close the gap between these bounds. This approach often exhibits advantages in terms of convergence speed and ability to handle constraints. In safe reinforcement learning, a primal-dual algorithm might be used to balance reward maximization (primal) with safety constraints (incorporated into the dual). The algorithm’s efficiency depends on the specific problem structure, the choice of update rules, and the handling of uncertainty in real-world applications. Convergence guarantees and sample complexity bounds are essential theoretical aspects of primal-dual algorithms for RL, ensuring reliable and efficient learning.
Partial Coverage#
The concept of ‘Partial Coverage’ in offline reinforcement learning is crucial because it addresses the limitations of traditional methods that require complete data coverage. Complete coverage is often unrealistic and impractical, especially in real-world settings where data collection is expensive or risky. Partial coverage acknowledges that we may not have data for all possible state-action pairs, especially those representing rare or hazardous situations. This relaxation makes offline RL more applicable, since it acknowledges real-world data scarcity. However, this relaxation introduces challenges in learning an optimal policy reliably. The theoretical guarantees and algorithms need to account for the uncertainty introduced by the missing data, often using techniques like pessimism or importance weighting to address the distribution shift between the observed data and the true underlying dynamics. Research focuses on developing robust learning methods that still produce reliable and safe policies under partial data coverage, demonstrating improved sample efficiency compared to approaches that assume full coverage. The success hinges on carefully balancing the risk of overestimation with the improved practicality of the partial coverage assumption. Developing bounds to quantify the impact of partial coverage is a key research area, enabling the design of algorithms with theoretical guarantees.
Offline Convex MDP#
Offline Convex Markov Decision Processes (MDPs) present a unique challenge in reinforcement learning. Unlike standard MDPs, offline settings restrict interaction with the environment, relying solely on pre-collected data. This introduces significant hurdles because the data distribution may not align with the optimal policy’s occupancy measure, leading to distribution shift issues. The convexity of the problem adds complexity, as the objective function isn’t necessarily linear in state-action occupancy. The typical Bellman equation approach, commonly used in standard MDPs, is no longer directly applicable, requiring innovative techniques to tackle the optimization problem. Therefore, algorithms designed for offline convex MDPs need to cleverly address both the data limitations (partial data coverage) and the mathematical challenges posed by the convex objective, developing approaches like marginalized importance weighting to mitigate distribution shifts and leveraging primal-dual methods for efficient optimization.
Sample Complexity#
Sample complexity in machine learning, especially within the context of reinforcement learning, is a crucial concept that quantifies the number of data samples needed to achieve a certain level of performance. In offline reinforcement learning, where interactions with the environment are limited, sample complexity is paramount as it directly impacts the feasibility and efficiency of the learning process. This research paper tackles this challenge head-on, focusing on offline convex constrained Markov Decision Processes (CMDPs) and achieving a significant improvement in sample complexity. The authors demonstrate a sample complexity of O(1/(1-γ)√n), which is notably better than the state-of-the-art. This improvement is attributed to a novel primal-dual method and the incorporation of uncertainty parameters, effectively handling partial data coverage. The theoretical analysis rigorously supports these claims, and the results are further validated through numerical experiments. The 1/(1-γ) factor highlights the efficiency gains, particularly crucial in settings with high discount factors, emphasizing the practical significance of the improvement. The work also extends beyond standard CMDPs to convex CMDPs, enhancing the applicability and generality of the findings. This improved sample complexity significantly advances offline safe reinforcement learning, opening up new possibilities for real-world applications.
Future Work#
Future research directions stemming from this offline safe reinforcement learning work could explore several promising avenues. Extending the theoretical analysis to non-convex CMDPs would significantly broaden the applicability of the primal-dual method. This would involve developing novel techniques to handle the complexities introduced by non-convexity, potentially leveraging advanced optimization methods or approximation schemes. Another crucial direction is improving sample efficiency further. While the current sample complexity is already state-of-the-art, exploring alternative algorithmic approaches, such as those based on pessimism or bootstrapping, could lead to even better performance in data-scarce settings. Furthermore, developing more sophisticated methods for handling uncertainty in the offline dataset is vital. Investigating robust optimization techniques or incorporating adaptive strategies to learn uncertainty parameters during training would enhance the algorithm’s ability to deal with noisy or incomplete data. Finally, applying this framework to real-world scenarios with stringent safety requirements, such as autonomous driving or robotics control, will be an important next step. This will require careful consideration of practical constraints and validation in realistic environments to demonstrate its efficacy and reliability in complex, high-stakes applications.
More visual insights#
More on figures
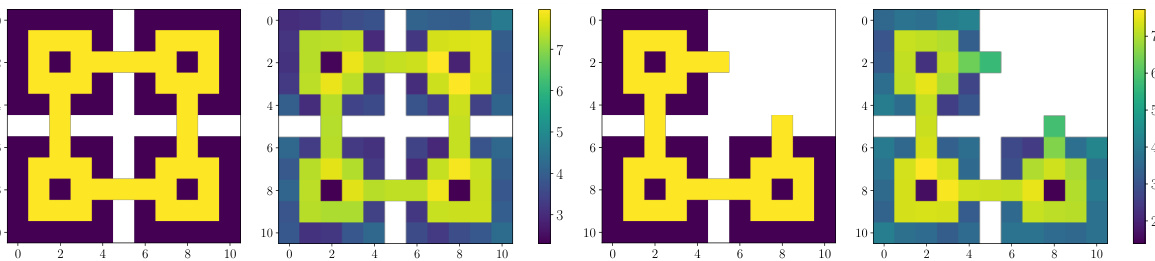
🔼 This figure shows the results of safe imitation learning experiments in a maze environment. Panel (a) displays the expert demonstrations used for training. Panel (b) illustrates the learned policy’s log-density when safety constraints are ignored, and panel (c) shows the target demonstrations incorporating safety constraints (costs assigned to states in the top-right corners). Finally, panel (d) presents the learned policy log-density when safety constraints are considered. The figure demonstrates the ability of the proposed algorithm to successfully learn a safe policy even with partial data.
read the caption
Figure 2: Reading order: (a) target demonstrations in yellow, wall in white; (b) result for log-density without considering the safety constraint; (c) target demonstrations that all states in top-right corners have cost; (d) result for log-density with safety constraint.
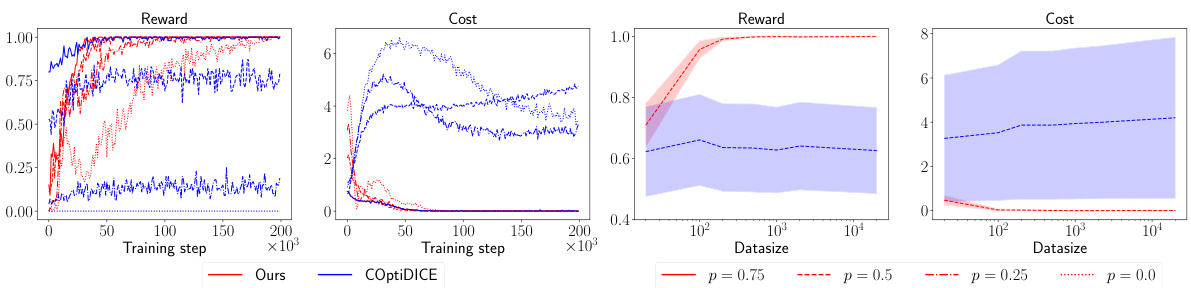
🔼 The figure presents the results of the proposed algorithm (POCC) and the baseline algorithm (COptiDICE) on the FrozenLake environment. Subfigures (a) and (b) show the learning curves for reward and cost respectively, comparing the performance of both algorithms under four different behavior policies (p = 0.75, 0.5, 0.25, 0.0, representing the percentage of optimal policies in the dataset). Subfigures (c) and (d) illustrate how the reward and cost vary with different dataset sizes for a fixed behavior policy (p=0.5). Error bars represent the average over 10 independent runs.
read the caption
Figure 3: Performance on FrozenLake with general function approximation. Reading order: (a) and (b) show the training result with four different behavior policies of COptiDICE and ours. (c) and (d) demonstrate the variations in rewards and costs as the dataset increases. Each point is the average result of 10 independent runs.
Full paper#