Adaptive Labeling for Efficient Out-of-distribution Model Evaluation

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers facing the challenge of reliable model evaluation under distribution shifts. It provides a novel framework that directly addresses this issue, offering a cost-effective solution. The method’s agnosticism to uncertainty quantification techniques and its empirical success across synthetic and real datasets make it broadly applicable and highly impactful. Furthermore, the work opens avenues for improving active learning strategies and developing more sophisticated adaptive sampling techniques.

Visual Insights

#

This figure illustrates the problem of selection bias in model evaluation. The left panel shows a dataset with labels only available for a subset of data points, leading to an underestimation of the mean squared error (MSE). The right panel shows that by adaptively selecting which points to label, the uncertainty in MSE can be reduced, particularly for regions not well represented in the original data set. The adaptive approach focuses on labeling examples to improve the estimation of the model’s performance outside the support of the available data.

This table presents the results of the experiment using Ensemble+ as the uncertainty quantification module. It compares the performance of various algorithms in terms of the variance and error of the estimated l2 loss. The algorithms compared include random sampling, uncertainty sampling (static and sequential), REINFORCE, and the proposed Autodiff 1-lookahead method.

In-depth insights

#

Adaptive Label Planning

#

Adaptive label planning addresses the challenge of efficiently evaluating machine learning models, especially in scenarios with significant distribution shifts and high labeling costs. The core idea is to strategically select which data points to label next, optimizing the information gained per label. This contrasts with traditional active learning, which often focuses solely on improving model accuracy. Instead, adaptive label planning prioritizes reducing uncertainty about the model’s overall performance across the entire distribution of unseen data. This involves framing the problem as a sequential decision-making process, often modeled as a Markov Decision Process (MDP), where the state represents the current knowledge about model performance, actions correspond to selecting batches of data points for labeling, and the reward reflects the reduction in uncertainty. Efficient algorithms are crucial, as exploring all possible label combinations is computationally prohibitive. Pathwise policy gradients provide a particularly powerful approach to finding optimal policies due to their lower variance compared to REINFORCE. The framework’s flexibility allows adaptation to different uncertainty quantification methods, making it applicable to a range of models and tasks. Successfully balancing exploration (discovering unknown aspects of model behavior) and exploitation (labeling data that most effectively reduces uncertainty) remains a key challenge, with lookahead policies offering better performance than simpler, myopic strategies.

Pathwise Policy Gradients

#

Pathwise policy gradients offer a powerful alternative to traditional score-function methods for policy gradient estimation in reinforcement learning and sequential decision-making problems. Unlike score-function methods, which suffer from high variance, pathwise methods leverage the known dynamics of the system to compute gradients with significantly lower variance. This is achieved by differentiating through simulated rollouts or trajectories of the system, effectively backpropagating the observed rewards through the system’s dynamics. The key advantage is that it circumvents the high-variance problem inherent in REINFORCE, facilitating more efficient and stable policy optimization, particularly in complex settings with noisy or stochastic environments. However, pathwise methods are only applicable when the system’s dynamics can be either known or accurately approximated. This makes the applicability of the method reliant on the availability of a differentiable model of the environment or system.

OOD Evaluation Metrics

#

Effective evaluation of out-of-distribution (OOD) generalization demands robust metrics. Standard in-distribution metrics often fail to capture performance in unseen scenarios. Novel metrics must account for uncertainty, distribution shifts, and the cost of errors in real-world applications. For example, a medical diagnosis model should be evaluated not only on accuracy but also on its ability to reliably identify cases where it lacks confidence, avoiding potentially harmful misdiagnoses. Therefore, beyond simple accuracy, we need metrics that consider the trade-off between true and false positives/negatives across different OOD subsets, potentially incorporating epistemic uncertainty. Ideally, a suite of OOD metrics, tailored to the specific application and risk tolerance, should be used for a comprehensive evaluation. The development of such metrics is critical for promoting the safe and reliable deployment of AI systems.

UQ Module Agnosticism

#

The concept of ‘UQ Module Agnosticism’ in the context of adaptive labeling for model evaluation highlights a crucial advantage: flexibility. Instead of being tied to a specific uncertainty quantification (UQ) method, the proposed framework can seamlessly integrate various UQ approaches. This is significant because different UQ methods have varying strengths and weaknesses depending on data characteristics and model complexity. This modular design enhances the framework’s applicability and robustness across diverse settings. By allowing researchers to choose the most suitable UQ method for their specific needs, the framework becomes more adaptable and less constrained by the limitations of any single UQ technique. The ability to swap in different UQ modules without altering the core adaptive labeling process speaks volumes about the framework’s elegant and practical design. This makes it more accessible and less reliant on specialized knowledge of a particular UQ method, thus lowering the barrier to entry for broader adoption and exploration.

Scalability Challenges

#

Scalability is a critical concern in adaptive labeling, especially when dealing with high-dimensional data or complex models. Computational cost increases significantly with the number of data points and the complexity of the uncertainty quantification method used. High-variance gradient estimators, such as REINFORCE, are unreliable for multi-step lookahead policies because their variance grows exponentially with the planning horizon. The combinatorial action space arising from selecting batches of data for labeling poses a significant challenge for efficient optimization. Auto-differentiation, while offering a promising pathway for gradient estimation, faces its own scalability challenges as higher-order gradients can become computationally expensive and numerically unstable. Approximations, such as smoothing techniques, can help to alleviate some of these challenges but may introduce bias. Thus, the development of efficient and scalable algorithms for adaptive labeling remains an open problem. Further research should focus on developing novel optimization methods tailored for the specific challenges of this problem, exploring alternative uncertainty quantification approaches with more manageable computational demands, and investigating approximation strategies that balance bias and variance effectively.

More visual insights

#

More on figures

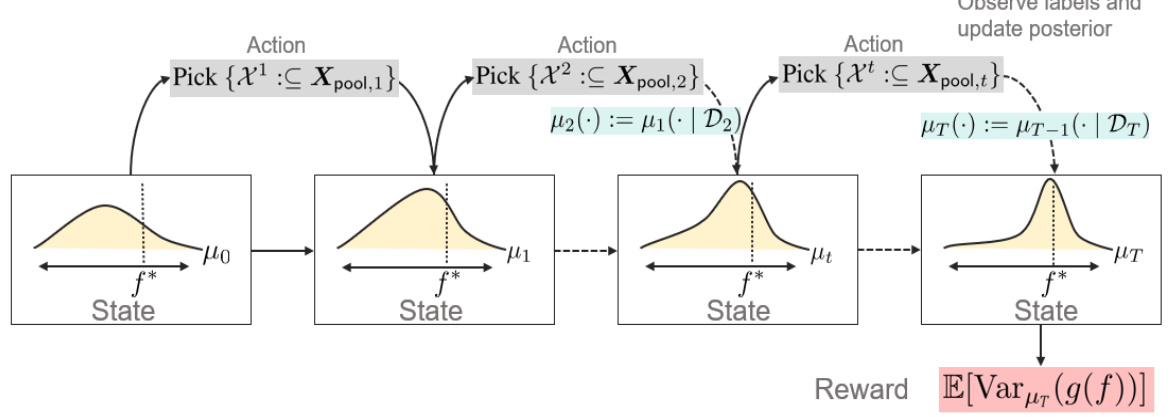
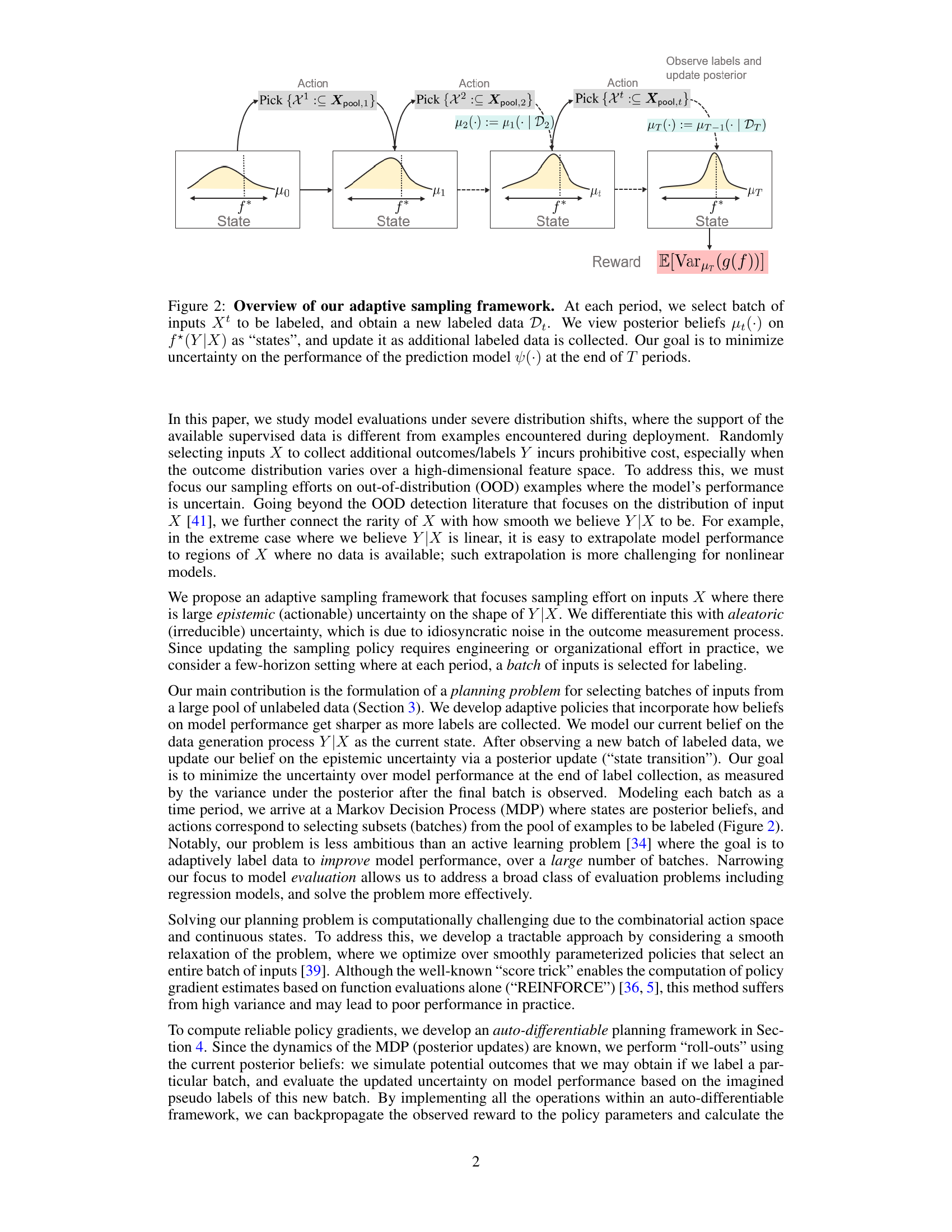
This figure illustrates the adaptive sampling framework presented in the paper. The framework is modeled as a Markov Decision Process (MDP). Each state in the MDP represents the posterior belief on the model’s performance, which is updated with each new batch of labels. The actions consist of selecting a subset of inputs from a pool of unlabeled data to be labeled. The goal of the MDP is to minimize the uncertainty in model performance after a fixed number of labeling periods (T). The figure visually shows the progression through states and actions, ultimately leading to the final state and a reward calculation based on the variance of the model’s performance.

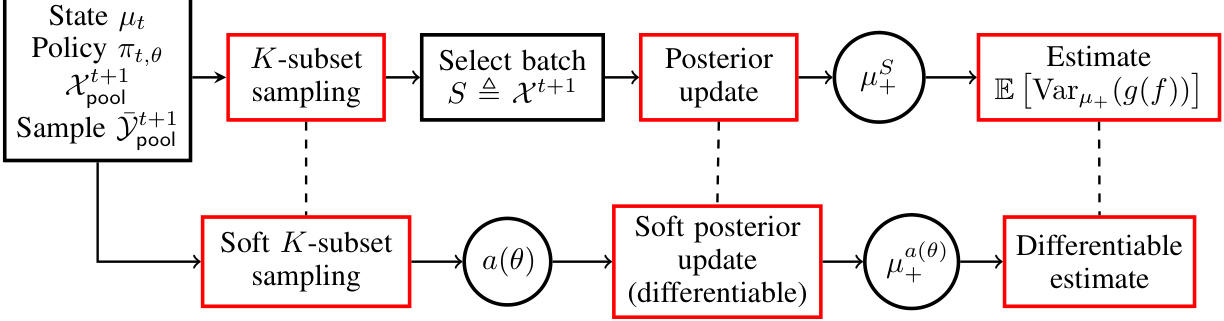
This figure illustrates the differentiable one-step lookahead pipeline used for efficient adaptive sampling. The pipeline begins with the current posterior belief (state μt) and policy (πt,θ). A batch of inputs (Xt+1) is sampled from the pool using K-subset sampling. Then, the selected batch is used to update the posterior belief (μt+1). The variance of the model performance (g(f)) is estimated from this updated posterior. The bottom path shows the differentiable version of this pipeline. The soft K-subset sampling is used to create a differentiable approximation of sampling, allowing for the use of smooth, differentiable posterior updates and a differentiable estimate of the model’s performance variance. This allows for efficient gradient-based policy optimization through backpropagation.

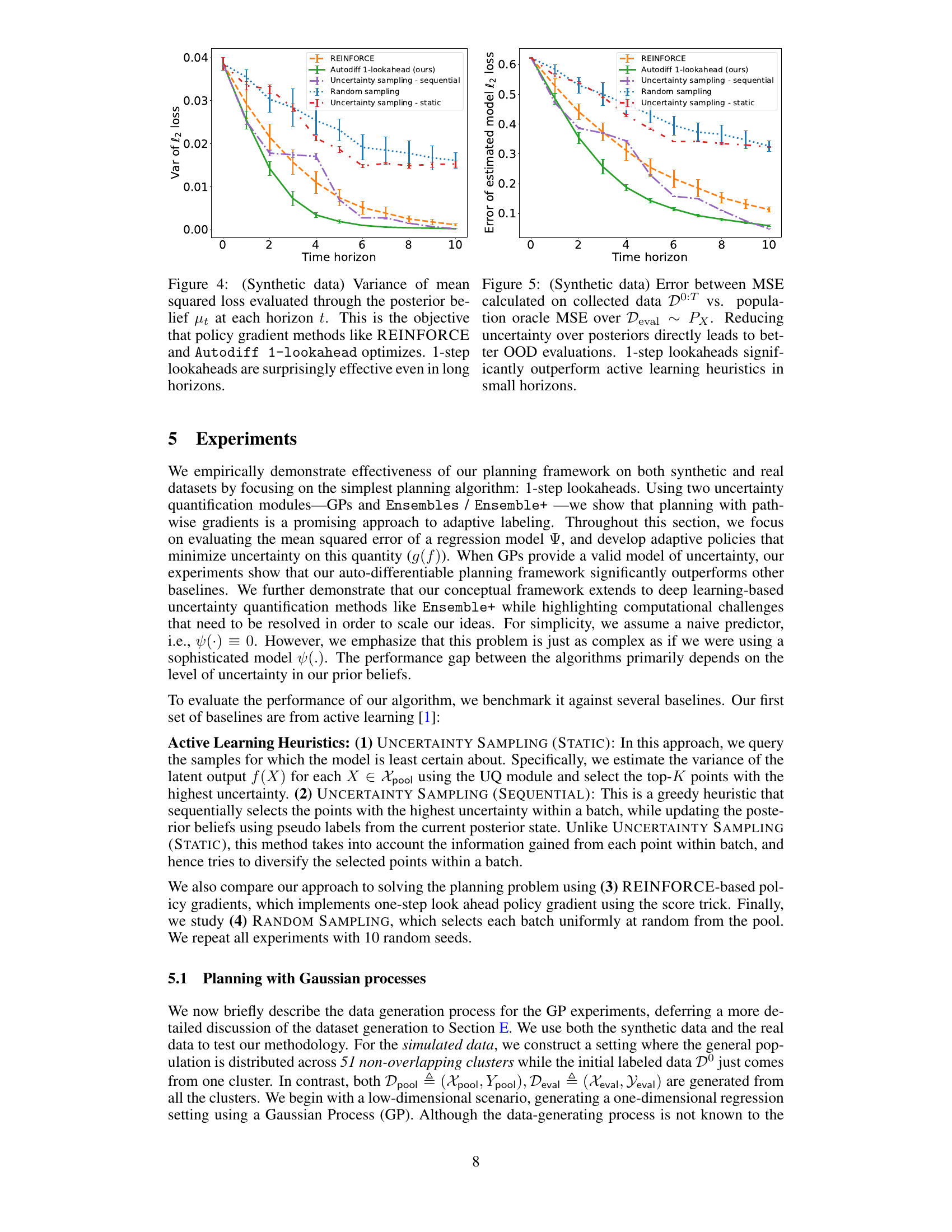
The figure shows the variance of the mean squared loss calculated using the posterior belief at each time step (horizon). It compares the performance of different methods for adaptive sampling: REINFORCE, the proposed Autodiff 1-lookahead method, and several uncertainty sampling heuristics (static and sequential). The graph demonstrates that even a one-step lookahead policy significantly reduces uncertainty in estimating model performance, even over longer time horizons.

The figure shows the variance of the mean squared loss (MSE) evaluated using the posterior belief at different time horizons (t) for various methods including REINFORCE, Autodiff 1-lookahead, uncertainty sampling (sequential and static), and random sampling. It illustrates how the variance of the MSE changes as more data is collected. The results demonstrate the effectiveness of the proposed Autodiff 1-lookahead method, even in longer time horizons, at reducing the uncertainty in the MSE estimate.

This figure shows a detailed overview of the differentiable one-step look-ahead pipeline used in the adaptive sampling framework. It illustrates how posterior beliefs (states) are updated using a soft K-subset sampling procedure and a differentiable posterior update method. The pipeline combines soft K-subset sampling, a differentiable posterior update method, and a differentiable estimate of the variance of MSE to efficiently optimize the policy and adapt the sampling strategy. The algorithm proceeds by: 1) obtaining a posterior state based on the data collected thus far; 2) using the policy to select a set of K inputs from a pool of unlabeled data; 3) using the UQ module (e.g., Gaussian Processes or neural network ensembles) to generate imagined pseudo labels and update the posterior; and 4) estimating the variance of MSE to compute the policy gradient for updating the policy using backpropagation. This process is repeated at each iteration. By making each step differentiable, the authors enable the use of efficient optimization methods like gradient descent to learn the optimal adaptive labeling policy.

Full paper

#