TL;DR#
Reinforcement learning (RL) often struggles with continuous control tasks due to limitations of unimodal policies like Gaussian policies. Diffusion models, known for their expressiveness and multimodality, show promise in addressing this but their integration in online RL remains less explored. Existing methods either suffer from the unavailability of ‘good’ samples or inaccurate Q-function gradients, hindering performance.
This research introduces QVPO, a novel model-free online RL algorithm. QVPO uses a Q-weighted variational loss, which provides a tight lower bound of the policy objective, and addresses the issue of exploration with a special entropy regularization term. To reduce variance, it employs an efficient behavior policy for action selection. Experiments on MuJoCo continuous control tasks demonstrate QVPO’s superior performance, achieving state-of-the-art results in cumulative reward and sample efficiency.
Key Takeaways#
Why does it matter?#
This paper is highly important because it presents a novel model-free online RL algorithm using diffusion models, a current research trend. It addresses limitations of existing online RL methods when integrating diffusion models and enhances the exploration and efficiency. This opens avenues for improved RL in continuous control tasks and inspires further research into enhancing diffusion models for online RL settings.
Visual Insights#
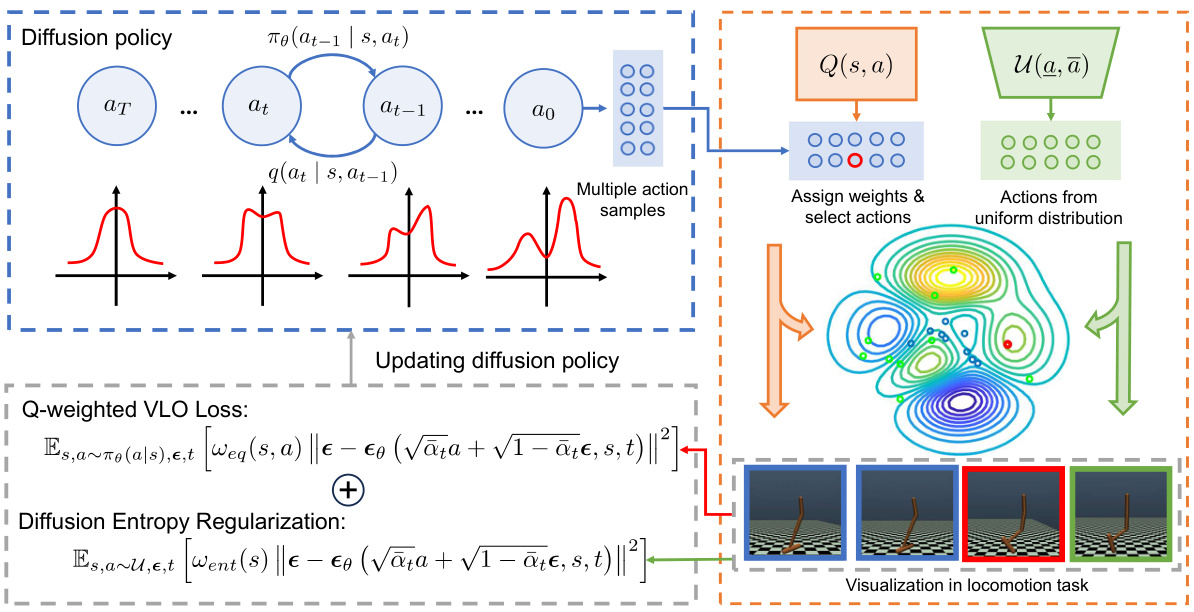
🔼 This figure illustrates the training pipeline of the Q-weighted Variational Policy Optimization (QVPO) algorithm. It shows how the algorithm uses a diffusion policy to generate action samples, assigns weights based on the Q-value from a value network, incorporates samples from a uniform distribution for entropy regularization, and updates the diffusion policy using the combined Q-weighted VLO loss and diffusion entropy regularization.
read the caption
Figure 1: The training pipeline of QVPO. In each training epoch, QVPO first utilizes the diffusion policy to generate multiple action samples for every state. Then, these action samples will be selected and endowed with different weights according to the Q value given by the value network. Besides, action samples from uniform distribution are also created for the diffusion entropy regularization term. With these action samples and weights, we can finally optimize the diffusion policy via the combined objective of Q-weighted VLO loss and diffusion entropy regularization term.

🔼 This table compares the performance of QVPO against six other online reinforcement learning algorithms (PPO, SPO, TD3, SAC, DIPO, and QSM) across five different MuJoCo locomotion tasks. The results show the average episodic reward and standard deviation achieved by each algorithm after 1 million training epochs. QVPO demonstrates superior performance across all tasks.
read the caption
Table 1: Comparison of QVPO and 6 other online RL algorithms in evaluation results. (N/A indicates the algorithm does not work)
In-depth insights#
Diffusion in RL#
Diffusion models have emerged as a powerful tool in reinforcement learning (RL), offering enhanced expressiveness and multimodality compared to traditional approaches. Their ability to capture complex data distributions is particularly advantageous in continuous control tasks, where overcoming the limitations of unimodal policies is crucial. While initially explored extensively in offline RL settings, research is increasingly focusing on integrating diffusion models into online RL algorithms. Challenges remain in directly applying diffusion models’ variational lower bound training objective in online settings due to the unavailability of good samples; however, this is actively being addressed via novel techniques. Exploration and efficiency are key considerations, requiring specialized entropy regularization methods to counter the inaccessibility of log-likelihoods inherent in diffusion policies and careful design of efficient behavior policies to mitigate high variance. Overall, the use of diffusion in RL represents a promising area of ongoing research with the potential to significantly advance the capabilities of RL agents, particularly in complex and high-dimensional environments.
QVPO Algorithm#
The QVPO algorithm presents a novel approach to online reinforcement learning by integrating diffusion models. Its core innovation lies in the Q-weighted variational loss, which cleverly combines the strengths of diffusion models’ expressiveness with the RL objective. Unlike prior methods that struggle with applying diffusion models to online RL, QVPO addresses the unavailability of ‘good’ samples by introducing Q-weights, which effectively guide the learning process. Furthermore, QVPO incorporates a novel entropy regularization term to improve exploration, a critical challenge with diffusion policies. Finally, the algorithm features an efficient behavior policy based on action selection to mitigate the large variance often associated with diffusion models, resulting in enhanced sample efficiency. Overall, QVPO offers a theoretically grounded and practically effective method for leveraging the power of diffusion models in the challenging domain of online RL, leading to improved performance in continuous control tasks.
Exploration Boost#
An ‘Exploration Boost’ section in a reinforcement learning (RL) research paper would likely detail methods for improving an RL agent’s ability to discover novel and rewarding states and actions. This is crucial because insufficient exploration can lead to the agent converging to suboptimal solutions. Effective exploration strategies are often problem-specific, but common approaches include exploration noise, adding randomness to action selection, or curiosity-driven exploration, where the agent is intrinsically motivated to explore unfamiliar states. The paper might also discuss exploration-exploitation trade-offs, the inherent tension between exploring unknown areas and exploiting already known rewards, and how the proposed method addresses this challenge. Entropy maximization, a technique to encourage diverse action selection, is another frequent element of exploration boosts. A key aspect of the section would be demonstrating the effectiveness of the proposed approach on benchmark tasks, potentially showing improved exploration metrics and consequently, better final performance. Theoretical analysis might prove the exploration boost’s effect on convergence properties, showing improvements in sample efficiency and robustness.
Variance Reduced#
The concept of ‘Variance Reduced’ in a reinforcement learning (RL) context likely refers to techniques aimed at mitigating the high variance often encountered in RL algorithms. High variance hinders stable learning, as updates can be erratic and unreliable. Variance reduction methods typically focus on improving the accuracy and consistency of the estimations involved in RL. This could involve strategies such as using importance sampling to correct for the bias introduced by off-policy learning or employing techniques like bootstrapping to reduce the impact of noisy data. Efficient behavior policies are another method to decrease variance; a well-designed behavior policy that guides exploration effectively ensures that the samples collected are more informative, leading to lower variance estimates. Furthermore, the use of value functions can contribute to variance reduction by providing a more stable target for policy updates, lessening the reliance on noisy immediate rewards. Regularization techniques, while often aimed at improving generalization, also implicitly reduce variance by discouraging extreme or unstable policy parameter values. Ultimately, effective variance reduction contributes significantly to improved sample efficiency and faster convergence in RL algorithms.
Future Works#
The ‘Future Works’ section of this research paper presents several promising avenues for future research. Extending the exploration capabilities of diffusion policies is a key area, potentially involving more sophisticated entropy regularization techniques or adaptive mechanisms to adjust the entropy term dynamically. Integrating entropy into the temporal difference (TD) target for soft policy iteration could enhance the algorithm’s ability to learn optimal policies. Another crucial area is improving the sample efficiency of the QVPO algorithm. This may require more advanced action selection techniques or better methods for handling the large variance inherent in diffusion models. Finally, applying the QVPO algorithm to more complex tasks and real-world scenarios would demonstrate its broader applicability and robustness. Thorough investigation of these avenues could significantly improve the algorithm’s performance and expand its utility in practical applications.
More visual insights#
More on figures
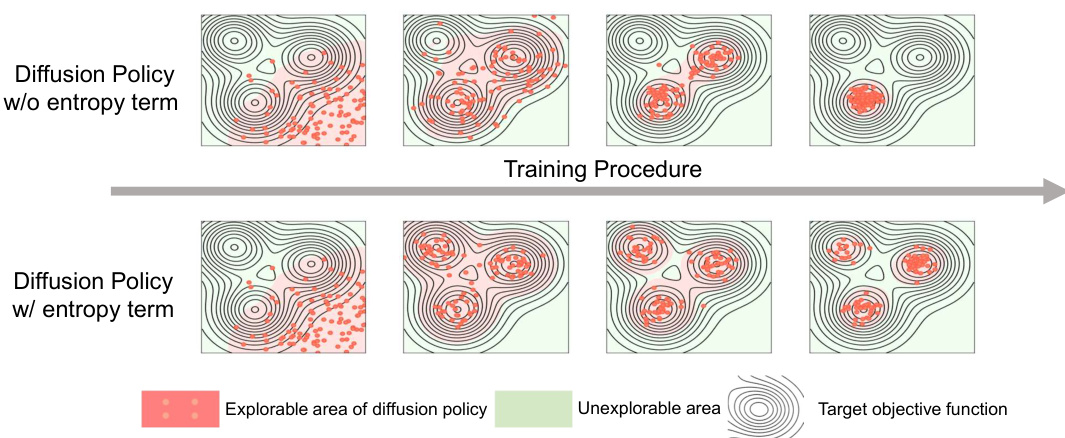
🔼 This figure shows a comparison of the explorable area of a diffusion policy with and without the entropy regularization term. The top row illustrates the diffusion policy without the entropy term, and the bottom row illustrates the diffusion policy with the entropy term. The contour lines show an arbitrarily selected reward function with three peaks. The red dots represent the action samples obtained during training, which demonstrate that the entropy term effectively expands the policy’s exploration range and helps it to discover areas with higher rewards.
read the caption
Figure 2: A toy example on continuous bandit to show the effect of diffusion entropy regularization term via the changes of the explorable area for diffusion policy with the training procedure. The contour lines indicate the reward function of continuous bandit, which is an arbitrarily selected function with 3 peaks.
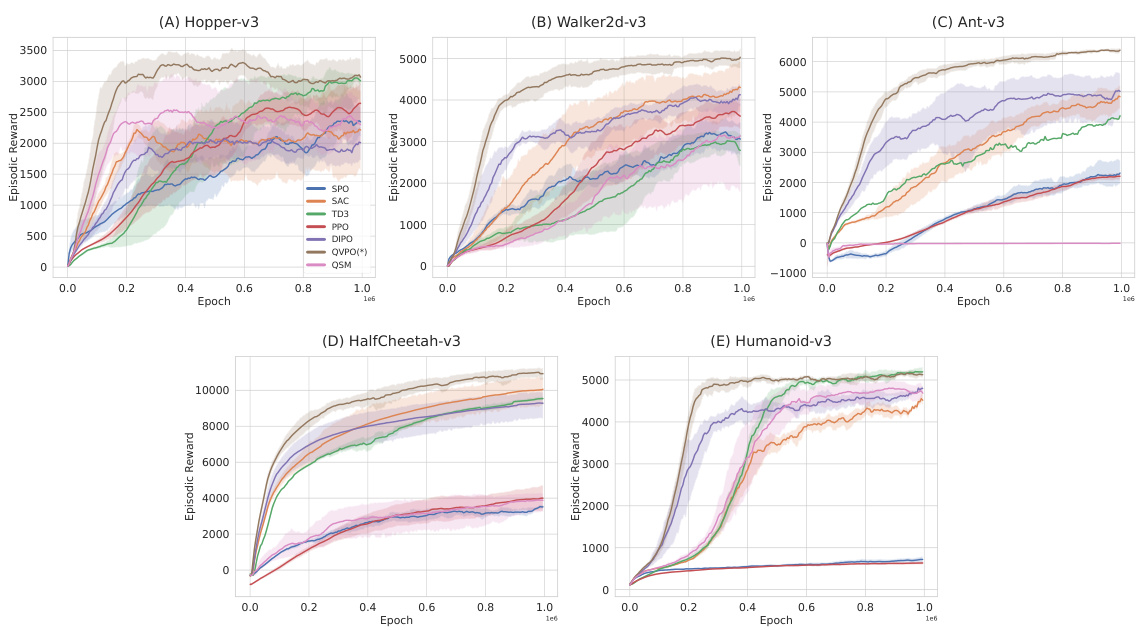
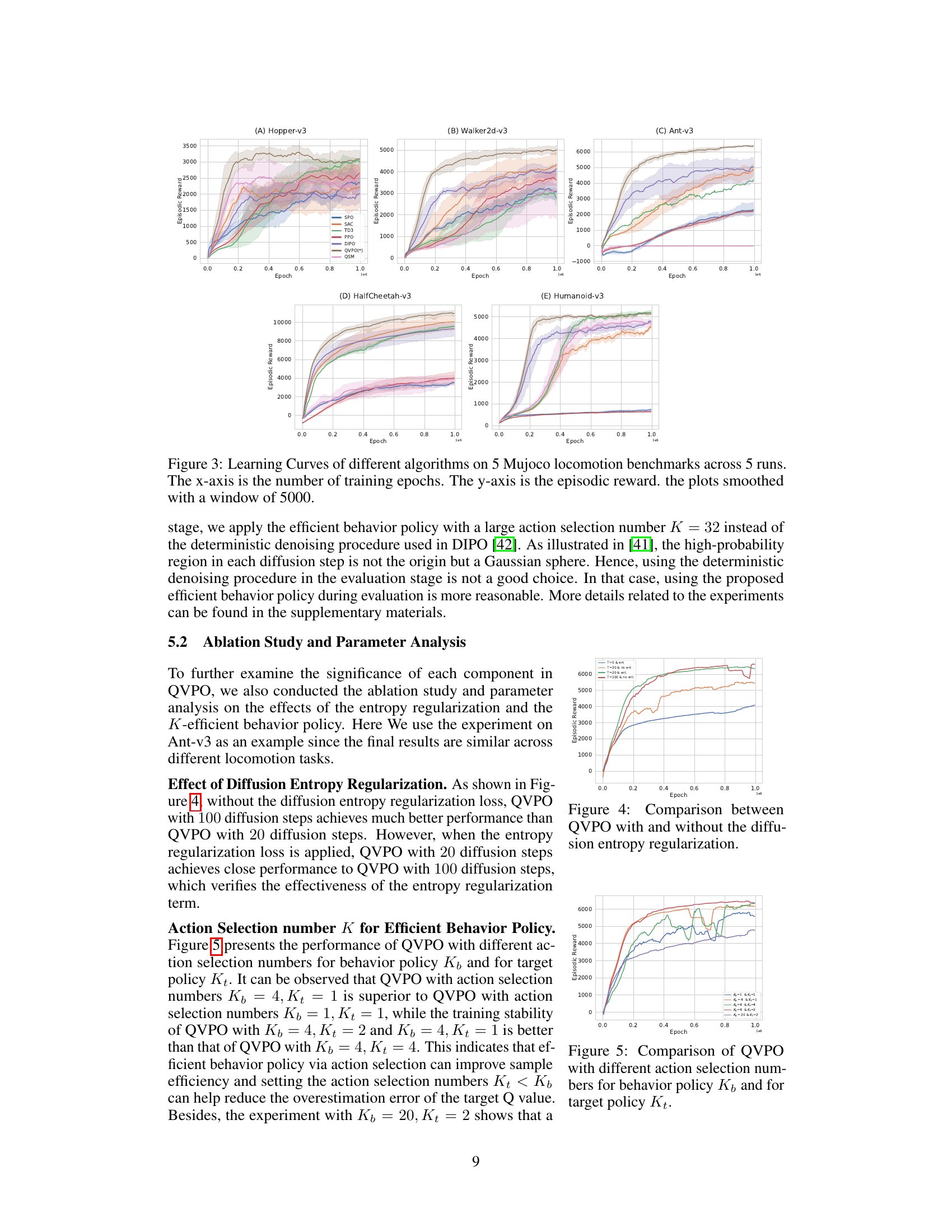
🔼 This figure shows the learning curves of different reinforcement learning algorithms on five MuJoCo locomotion tasks. Each algorithm was run five times, and the average episodic reward is plotted against the number of training epochs. The shaded areas represent the standard deviation across the five runs. The figure clearly demonstrates that QVPO converges faster and achieves higher rewards than other algorithms.
read the caption
Figure 3: Learning Curves of different algorithms on 5 Mujoco locomotion benchmarks across 5 runs. The x-axis is the number of training epochs. The y-axis is the episodic reward. the plots smoothed with a window of 5000.
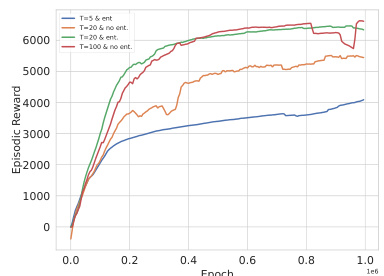
🔼 The figure shows the learning curves of QVPO on the Ant-v3 environment with different settings: 20 diffusion steps with and without entropy regularization, and 100 diffusion steps with and without entropy regularization. It demonstrates the impact of entropy regularization on the model’s performance, especially when the number of diffusion steps is limited (20). With entropy regularization, the performance with 20 steps comes close to that achieved with 100 steps without it, highlighting the effectiveness of entropy regularization in improving exploration and mitigating the performance loss due to fewer diffusion steps.
read the caption
Figure 4: Comparison between QVPO with and without the diffusion entropy regularization.
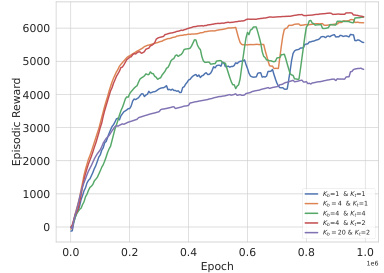
🔼 This figure shows the results of an ablation study on the effect of different action selection numbers (Kb for behavior policy and Kt for target policy) in the QVPO algorithm. It compares the episodic reward achieved by QVPO using different combinations of Kb and Kt values (Kb=1 & Kt=1, Kb=4 & Kt=1, Kb=4 & Kt=4, Kb=4 & Kt=2, Kb=20 & Kt=2). The results demonstrate the impact of action selection on the algorithm’s performance and sample efficiency. Different combinations lead to different levels of exploration and exploitation, influencing the final episodic reward.
read the caption
Figure 5: Comparison of QVPO with different action selection numbers for behavior policy K♭ and for target policy Kt.
More on tables
🔼 This table presents a comparison of the performance of QVPO against six other online reinforcement learning algorithms across five different MuJoCo locomotion tasks. The results show the mean episodic reward achieved by each algorithm, along with the standard deviation in parentheses. The algorithms compared are Proximal Policy Optimization (PPO), Twin Delayed Deep Deterministic Policy Gradients (TD3), Soft Actor-Critic (SAC), Simple Policy Optimization (SPO), Diffusion Policy Optimization (DIPO), and Q-Score Matching (QSM). The table highlights QVPO’s superior performance compared to the other methods.
read the caption
Table 1: Comparison of QVPO and 6 other online RL algorithms in evaluation results. (N/A indicates the algorithm does not work)

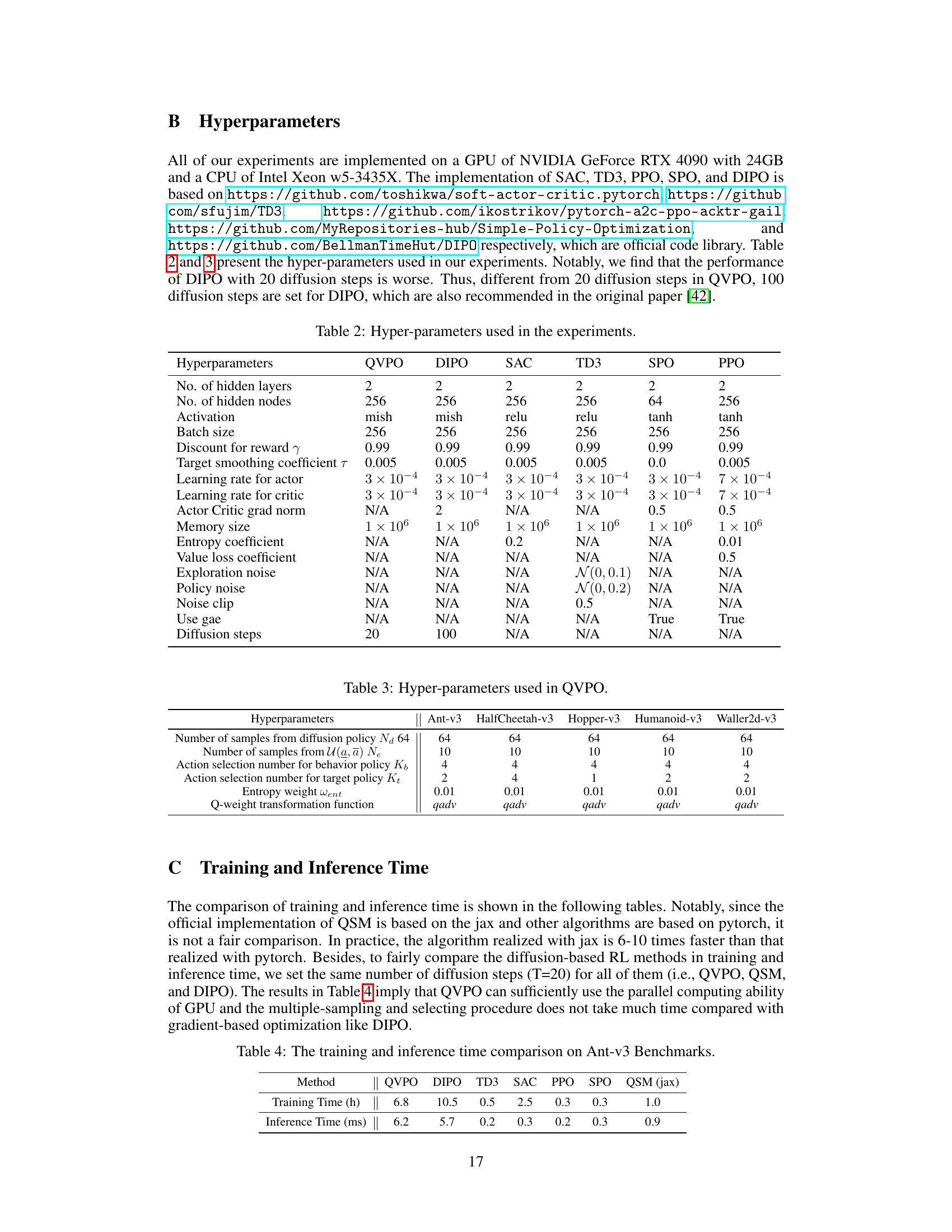
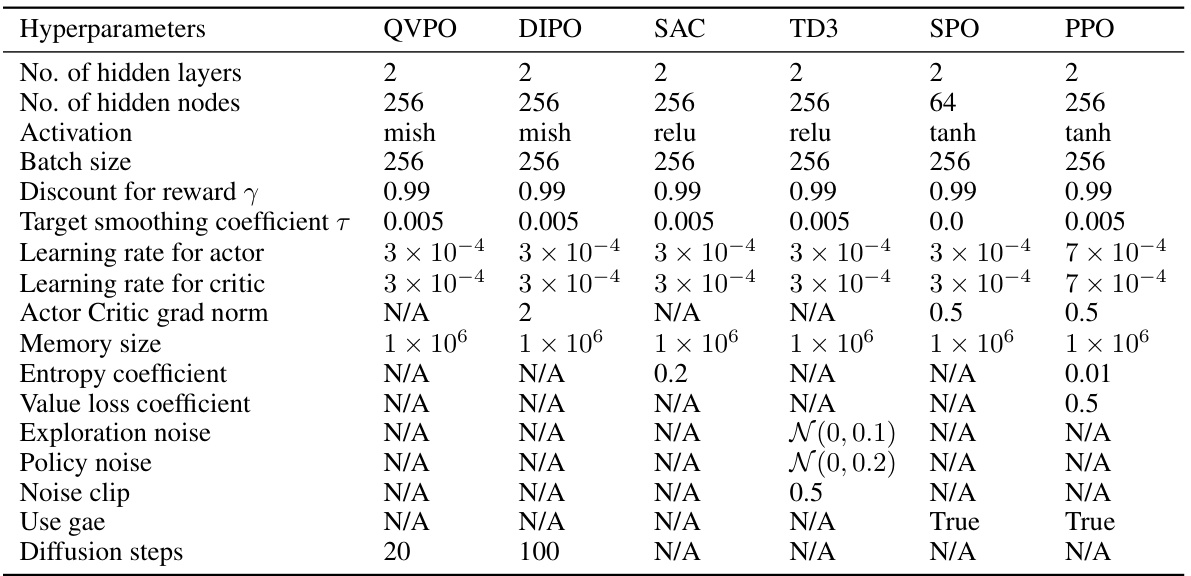
🔼 This table lists the hyperparameters used in the QVPO algorithm for each of the five MuJoCo locomotion tasks. It shows the number of samples drawn from the diffusion policy and a uniform distribution, the number of actions selected for behavior and target policies, the entropy weight, and the Q-weight transformation function used.
read the caption
Table 3: Hyper-parameters used in QVPO.

🔼 This table compares the performance of QVPO against six other online reinforcement learning algorithms across five MuJoCo locomotion tasks. The results show the mean episodic reward achieved by each algorithm, with standard deviations in parentheses. ‘N/A’ indicates that an algorithm did not successfully complete the task.
read the caption
Table 1: Comparison of QVPO and 6 other online RL algorithms in evaluation results. (N/A indicates the algorithm does not work)
Full paper#