↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Viral marketing strategies often aim to influence groups of people (motifs) rather than individuals. However, existing influence maximization (IM) methods often fail to capture the group dynamics effectively, leading to ineffective campaigns. This paper focuses on the motif-oriented influence maximization (MOIM) problem, which seeks to select a small set of initial users (seed nodes) that can maximize the activation of motifs within a social network. The challenge is that activating only part of a motif might not achieve the desired viral effect.
The authors propose a novel algorithm to address this challenge. The core of their approach involves establishing submodular upper and lower bounds for the influence function and then using a greedy strategy to maximize both bounds simultaneously. They demonstrate that their algorithm has a guaranteed approximation ratio and a near-linear time complexity, meaning it can scale well to large social networks. The algorithm’s effectiveness is validated through rigorous experiments on various datasets, demonstrating significant improvements over existing IM techniques. This research offers a more realistic and efficient way to design viral marketing strategies.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in viral marketing and social network analysis due to its novel approach to influence maximization. It addresses the limitations of traditional methods by focusing on motifs, thus offering a more realistic and effective way to model influence spread in social networks. The guaranteed approximation ratio and near-linear time complexity also make this research highly relevant to practitioners dealing with large-scale datasets, which are increasingly prevalent in social media analysis. The work opens new avenues for research, particularly in optimizing influence propagation considering diverse cascade models and real-world constraints.
Visual Insights#
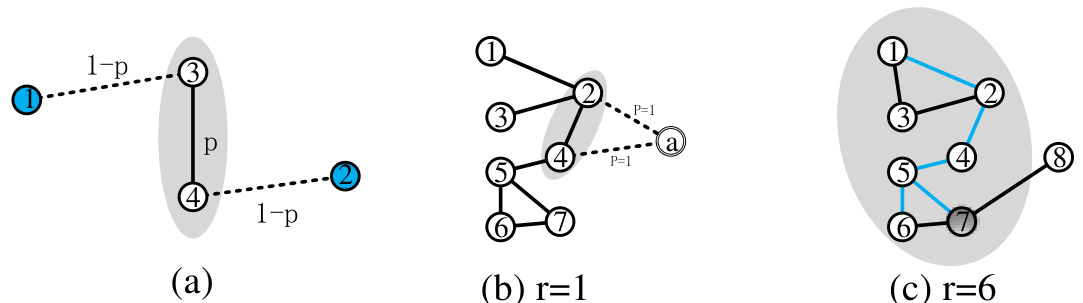
This figure illustrates three graph examples to explain concepts in the paper. (a) shows a simple graph with a single motif consisting of nodes 3 and 4. (b) demonstrates the concept of a ‘super node,’ which represents a motif and is connected to nodes within the motif with probability 1. (c) shows a 5-spanning tree, a subgraph within a motif that connects activated nodes to other nodes within the motif, crucial in the motif activation process. These illustrations help visualize the motif-oriented influence maximization problem and the proposed solution.

This table presents the characteristics of five real social networks used in the experiments. For each network, it lists the number of nodes (n), the number of edges (m), whether the network is directed or undirected, and the average degree of the nodes. These characteristics provide context for understanding the scale and structure of the datasets used in evaluating the influence maximization algorithm.
In-depth insights#
Motif-Oriented IM#
The concept of “Motif-Oriented IM” introduces a significant advancement in influence maximization (IM) by shifting the focus from individual nodes to interconnected groups, or motifs. Traditional IM methods treat each user as an independent entity, neglecting the crucial role of group dynamics in information diffusion. Motif-Oriented IM addresses this limitation by explicitly considering the structure and interdependencies within motifs. This approach recognizes that influencing a subset of users within a motif might not be as effective as targeting the entire group simultaneously, particularly in contexts where group consensus or coordinated action is required. This nuanced perspective leads to more effective viral marketing strategies. The challenge lies in the complexity of modeling motif activation, as the influence function is neither submodular nor supermodular, defying traditional IM optimization techniques. The solution often involves developing approximation algorithms that leverage upper and lower bounds to address the computational hardness while maintaining a reasonable approximation ratio. A key benefit of Motif-Oriented IM is its higher practical applicability, particularly in scenarios involving coordinated group behavior, social circles, or community dynamics, leading to more efficient and targeted campaigns compared to traditional IM approaches.
Greedy Algorithm#
A greedy algorithm, in the context of influence maximization, is a heuristic approach that iteratively selects the node that maximizes a local objective function at each step. It’s inherently myopic, focusing only on the immediate gain without considering the long-term consequences. In the specific case of motif-oriented influence maximization, this myopia is particularly relevant because the algorithm’s effectiveness depends heavily on the choice of the local objective function, which needs to be carefully crafted to capture the underlying complexities of motif activation. A key challenge lies in balancing the greedy algorithm’s simplicity with its potential for suboptimality. To improve the outcome, the algorithm may incorporate submodularity analysis by selecting nodes to improve both upper and lower bounds of the motif activation function simultaneously. This technique offers a trade-off, achieving near-optimal solutions in a reasonable amount of time by sacrificing some optimality to ensure efficiency.
Submodularity Bounds#
The concept of “Submodularity Bounds” in the context of influence maximization is crucial because the objective function, representing the spread of influence, is often not submodular. This lack of submodularity prevents the direct application of efficient greedy algorithms with guaranteed approximation ratios. Submodularity bounds provide a way to circumvent this challenge by framing the problem in terms of submodular functions that act as upper and lower approximations of the original non-submodular objective. By maximizing these bounds, an algorithm can indirectly maximize the original objective, achieving a balance between computational efficiency and solution quality. The tightness of these bounds directly impacts the quality of the approximation, with tighter bounds yielding better results. Developing effective submodularity bounds requires a deep understanding of the problem’s structure and properties. The choice of these bounds significantly influences the overall performance and approximation guarantees of the influence maximization algorithm. A good algorithm might utilize both upper and lower bounds simultaneously, optimizing a combination of them to achieve a robust solution.
NP-hardness Proof#
To rigorously demonstrate NP-hardness for a problem like influence maximization, a reduction from a known NP-complete problem is essential. A common approach involves reducing the problem to a known NP-complete problem, such as the Set Cover problem or the Maximum Clique problem. The reduction needs to show a polynomial-time transformation from an instance of the known NP-complete problem to an equivalent instance of the influence maximization problem. The core argument would demonstrate that solving the influence maximization problem efficiently would directly imply the efficient solution to the NP-complete problem, a contradiction under the assumption that P ≠ NP. This often involves constructing a graph representing the NP-complete problem’s instance, where nodes might represent elements and sets, and edges define relationships. Successfully showing the reduction provides compelling evidence of NP-hardness, signifying that finding the optimal solution for the influence maximization problem is computationally intractable for large-scale networks. However, proving NP-hardness doesn’t preclude the existence of effective approximation algorithms or heuristics for solving it in practice, which are often explored when dealing with NP-hard problems.
Future Extensions#
Future research directions stemming from this motif-oriented influence maximization work could explore several avenues. Extending the model to incorporate diverse motif structures and relationships beyond simple, strongly connected components is crucial. Investigating how motif activation thresholds influence overall effectiveness and exploring alternative diffusion models beyond linear threshold and independent cascade is vital. Developing more sophisticated algorithms with improved approximation guarantees and reduced time complexity is also a key area for improvement. Finally, a thorough investigation of the interplay between motif-oriented influence maximization and real-world applications (e.g., targeted advertising, viral marketing campaigns) is warranted, focusing on the practical challenges and limitations of implementation in complex social networks. This includes evaluating the impact of various factors like user behavior, information spread dynamics, and network structure on the efficiency and efficacy of the proposed approach.
More visual insights#
More on figures

This figure displays the performance of the motif influence function across four different datasets (Flickr, Amazon, Catster, Youtube) under the Linear Threshold (LT) model. The x-axis represents the number of seed nodes (k), and the y-axis represents the expected motif influence. Each subplot corresponds to a different dataset, showing how the expected motif influence increases with the number of seed nodes. The results suggest that the proposed method outperforms other existing methods in all four datasets.
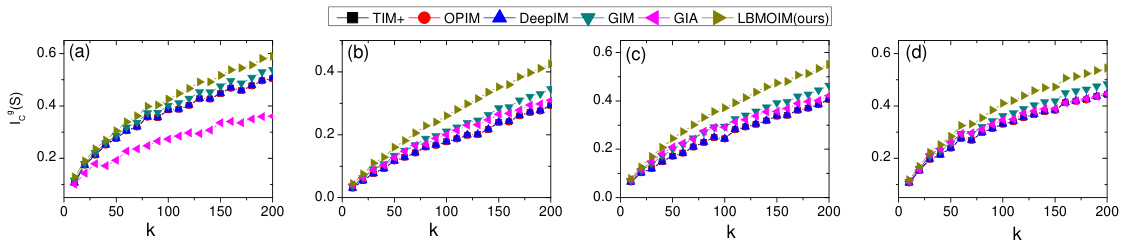
This figure displays the performance of different influence maximization algorithms across four different social network datasets (Flickr, Amazon, Catster, Youtube) under the Linear Threshold (LT) model. The x-axis represents the number of seed nodes (k), and the y-axis shows the expected number of activated motifs. Each subplot corresponds to a different dataset, demonstrating the algorithm’s effectiveness in activating motifs which represent groups of users. The algorithm LBMOIM (ours) consistently outperforms existing methods across all datasets.

This figure displays the performance of the motif influence function under the linear threshold (LT) model, where the threshold (r₁) is set to 1 and motif size is 2. The x-axis represents the number of seed nodes (k), while the y-axis shows the expected motif influence. The results are shown separately for four different datasets: Flickr, Amazon, Catster, and Youtube. The figure visually compares the performance of the proposed algorithm (LBMOIM) against other state-of-the-art methods (TIM+, OPIM, DeepIM, GIM, GIA). A higher value on the y-axis indicates better performance.

This figure displays the performance of different influence maximization methods across various datasets under the linear threshold (LT) model with a motif size of 2 and a threshold value (r₁) of 1. The x-axis represents the number of seed nodes (k), while the y-axis shows the expected motif influence, indicating the number of activated motifs. The figure demonstrates that the proposed LBMOIM method consistently outperforms other state-of-the-art algorithms on all four datasets (Flickr, Amazon, Catster, and Youtube).
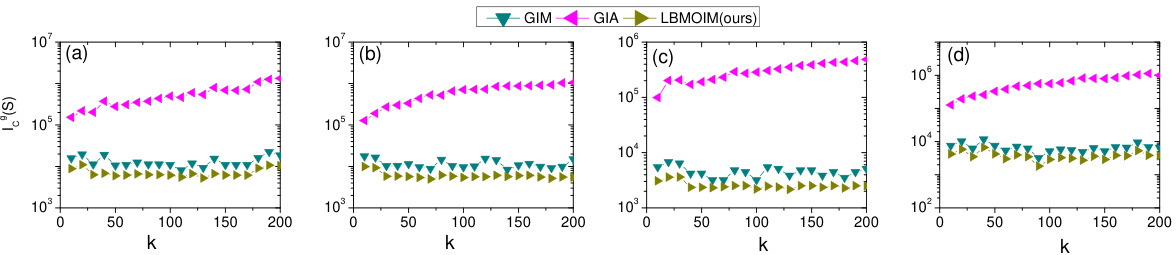
This figure compares the performance of different influence maximization algorithms (GIM, GIA, and LBMOIM) under the Independent Cascade (IC) model on the Douban dataset. It shows the expected number of activated motifs as a function of the number of seed nodes (k) for three different threshold values (r₁ = 1, 2, and 3). LBMOIM consistently outperforms the other algorithms.

This figure illustrates three concepts related to motif-oriented influence maximization. (a) shows a simple graph with one motif (a set of interconnected nodes). (b) introduces the concept of a ‘super node,’ representing a motif as a single node for simplification, connected to its constituent nodes with probability 1. (c) illustrates a ‘semi 5-spanning tree’, a subgraph connecting activated and inactive nodes within a motif. These figures help to explain the mathematical model and concepts used in the paper.
Full paper#



















