↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Deep neural networks, despite their impressive capabilities, often lack robustness—a significant hurdle for their use in safety-critical applications. Existing certification methods like Lipschitz continuity primarily focus on continuous domains and often fail to capture the nuances of discrete data like text, hindering their use in natural language processing. The inherent difficulty in defining distance metrics in discrete spaces compounds this challenge.
This research introduces a new framework called knowledge continuity to address these challenges. Instead of relying on traditional distance metrics, it focuses on the stability of a model’s loss function across its internal representations. This approach offers domain-independent robustness certification guarantees, meaning it works well for both continuous and discrete data. The researchers also developed practical applications such as a regularization algorithm and a certification method. Experiments demonstrate that knowledge continuity can effectively predict adversarial vulnerabilities and improve model robustness.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses the limitations of existing robustness certification methods, especially in discrete domains like natural language. It proposes a novel framework, knowledge continuity, that provides domain-independent robustness guarantees and opens up exciting avenues for research in certified robustness and related areas. The practical applications and algorithms presented enhance the utility of the findings for a broad range of researchers.
Visual Insights#
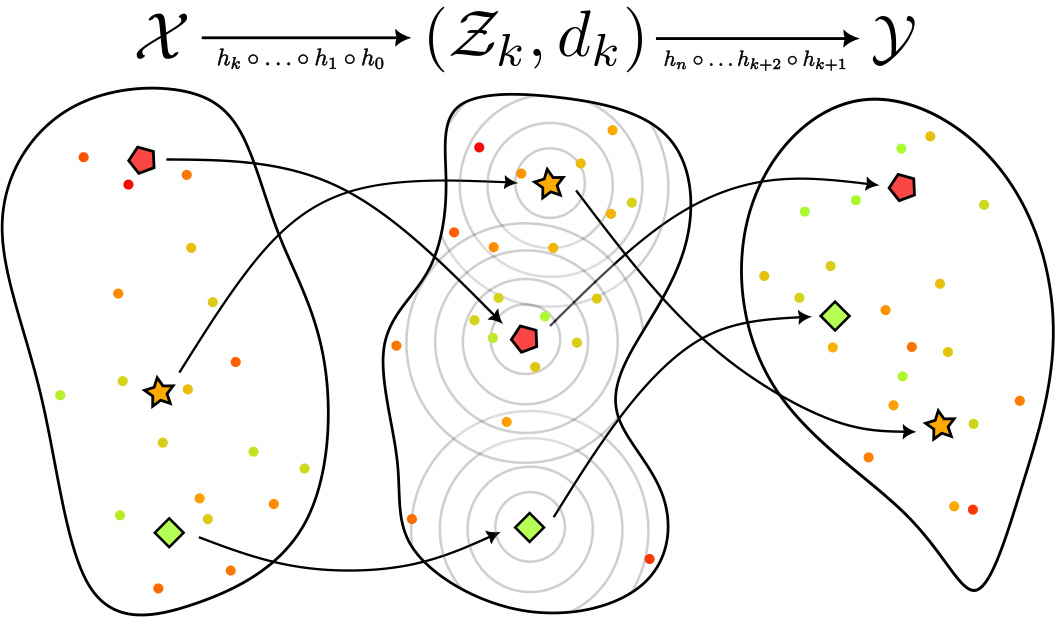
This figure illustrates three scenarios of knowledge continuity in a model’s hidden representation space. The color of the points represents the loss. A single point (★) surrounded by a large space shows sparse knowledge continuity where any small perturbation results in large changes in loss. A cluster of points (★) with smooth changes in loss nearby illustrates knowledge continuity. A point (◆) surrounded by a drastic change in loss exhibits knowledge discontinuity. Importantly, the classification of points is independent of the input-output space clustering since the input-output space might not have a metric.
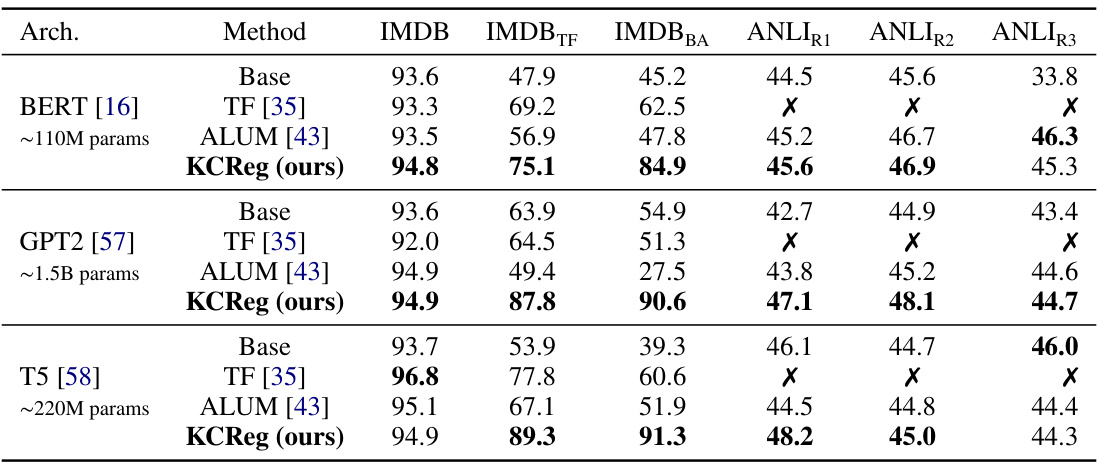
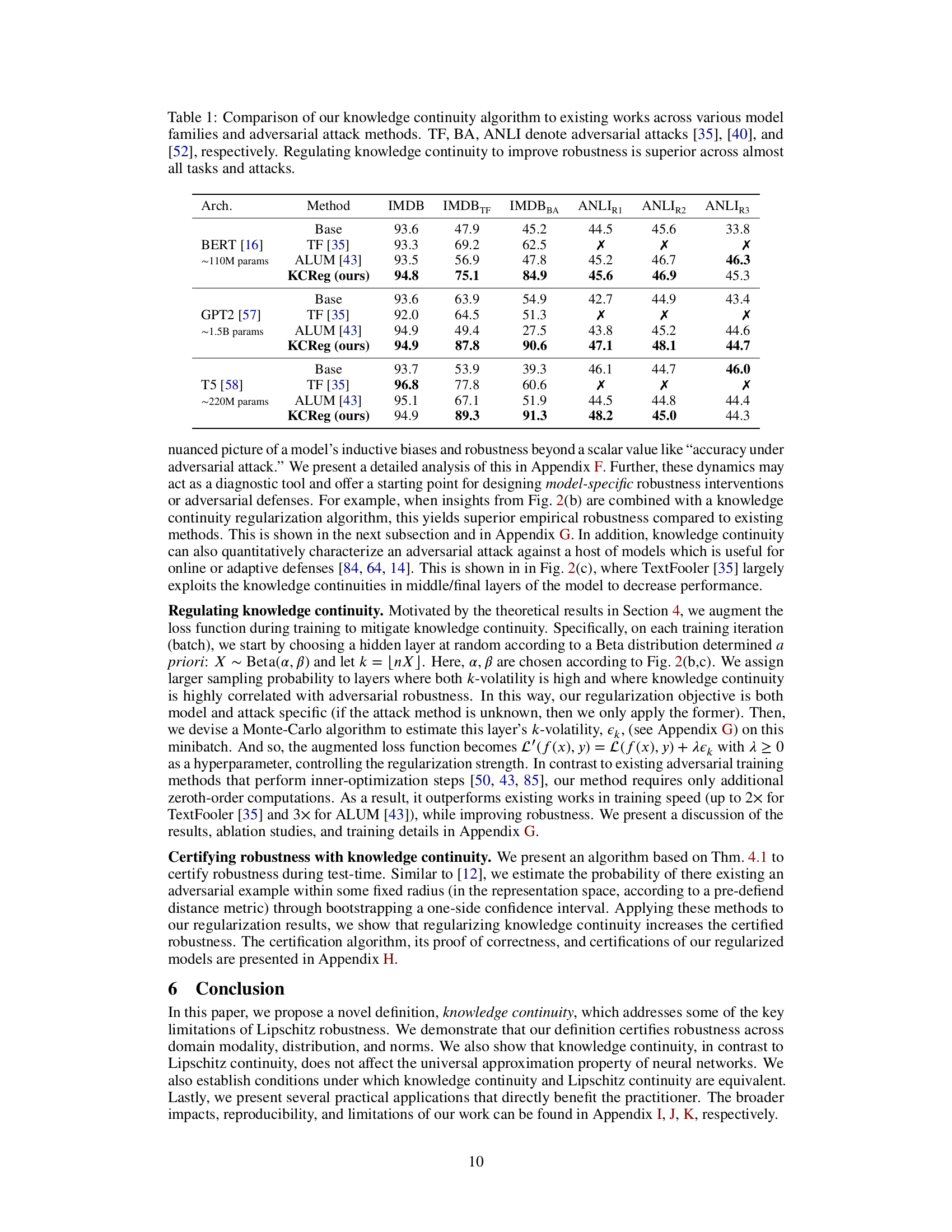
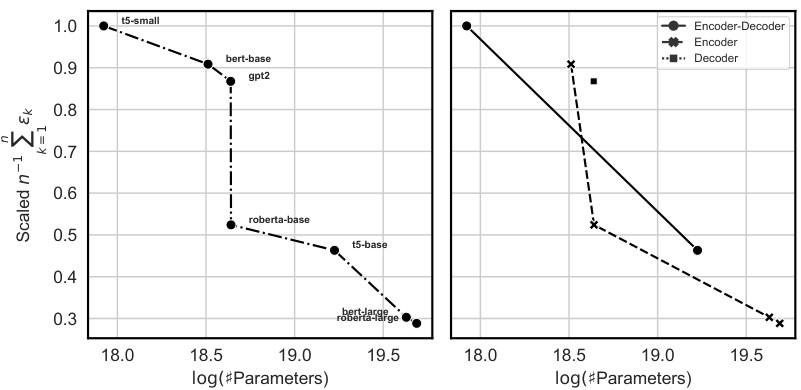
This table compares the performance of the proposed knowledge continuity regularization method (KCReg) against baseline methods (TextFooler, ALUM) across various models (BERT, GPT2, T5) and adversarial attacks (TextFooler, BA, ANLI). The results show that KCReg consistently improves robustness across all tasks and attacks.
In-depth insights#
Knowledge Continuity#
The core idea of “Knowledge Continuity” is to certify the robustness of neural networks by focusing on the stability of a model’s loss function concerning its hidden representations. This approach differs significantly from traditional methods like Lipschitz continuity which rely on input-output space metrics. Knowledge continuity is domain-independent, offering guarantees irrespective of whether the input domain is continuous (like images) or discrete/non-metrizable (like text). The authors propose that robustness is best achieved by focusing on the changes in loss, not directly on the input-output perturbations. Knowledge continuity generalizes Lipschitz continuity in continuous settings while accommodating the limitations of applying Lipschitz continuity to discrete domains. A key advantage is that high expressiveness in the model class does not conflict with knowledge continuity, implying that robustness can be achieved without sacrificing model performance. The practical applications of the framework include employing knowledge continuity to predict and characterize robustness and using it as a regularization term during training.
Certified Robustness#
The concept of “Certified Robustness” in the context of neural networks is explored, focusing on the challenges of guaranteeing robustness across diverse input domains. Traditional approaches, heavily reliant on Lipschitz continuity, often struggle with discrete or non-metrizable spaces like natural language. The paper introduces a novel approach, knowledge continuity, which offers domain-independent certification by focusing on the variability of a model’s loss function concerning its hidden representations, rather than imposing arbitrary metrics on inputs/outputs. This approach yields certification guarantees independent of domain modality, norms, and distribution. Importantly, the paper demonstrates that high expressiveness is not inherently at odds with knowledge continuity, implying robustness can be improved without sacrificing performance. The practical implications are substantial, with applications in regularization, vulnerability localization, and the development of a novel certification algorithm. This approach offers a significant advancement in the pursuit of robust and reliable AI systems.
Empirical Validation#
An Empirical Validation section would ideally present robust evidence supporting the claims made in the paper. This would involve designing experiments to rigorously test the core concepts of knowledge continuity, comparing its performance against existing methods like Lipschitz continuity, and demonstrating its effectiveness across various domains (e.g., computer vision, natural language processing). Key metrics would include adversarial attack success rates, accuracy, and computational efficiency. The experiments should be designed to isolate the impact of knowledge continuity, possibly via ablation studies. Visualization of results (e.g., graphs, tables) is essential for clear communication and should focus on clearly showing the effect of knowledge continuity on the performance metrics. Statistical significance testing should also be carefully conducted to ensure the reliability of results. Furthermore, the section should acknowledge any limitations or caveats related to the empirical validation, such as the datasets used, the types of adversarial attacks tested, or the specific model architectures considered. The overall strength of the empirical validation hinges upon the reproducibility and generalizability of the findings, with a well-designed methodology being crucial.
Limitations#
The research paper’s limitations section would critically examine the probabilistic nature of its certification guarantees, acknowledging that these guarantees don’t extend to out-of-distribution attacks, a significant vulnerability in large language models. The study should also address the restrictive assumptions underlying its expressiveness bounds, acknowledging that the trivial metric decomposition approach simplifies the model’s complexity. Furthermore, a thoughtful limitations analysis would discuss the naive Monte-Carlo algorithm used for k-volatility estimation, highlighting its computational limitations and the potential for improvement. Finally, the impact of hyperparameter choices, specifically α and β in the Beta distribution for layer selection, could be further investigated to understand their influence on model performance and robustness. A complete limitations section would address these critical aspects, enhancing the paper’s overall rigor and transparency.
Future Work#
Future research directions stemming from this work on knowledge continuity could explore several promising avenues. Extending the theoretical framework to encompass more complex model architectures, such as transformers with attention mechanisms, would enhance the practical applicability of the method. Developing more efficient algorithms for estimating k-volatility is crucial for scalability and real-time applications. Investigating the interplay between knowledge continuity and other robustness measures, such as adversarial training and randomized smoothing, could provide a more holistic understanding of model robustness. Finally, empirical evaluation on a wider variety of tasks and datasets, across different domains (e.g., time series analysis, medical imaging), is necessary to validate the generalizability of the proposed method and determine its potential limitations.
More visual insights#
More on figures
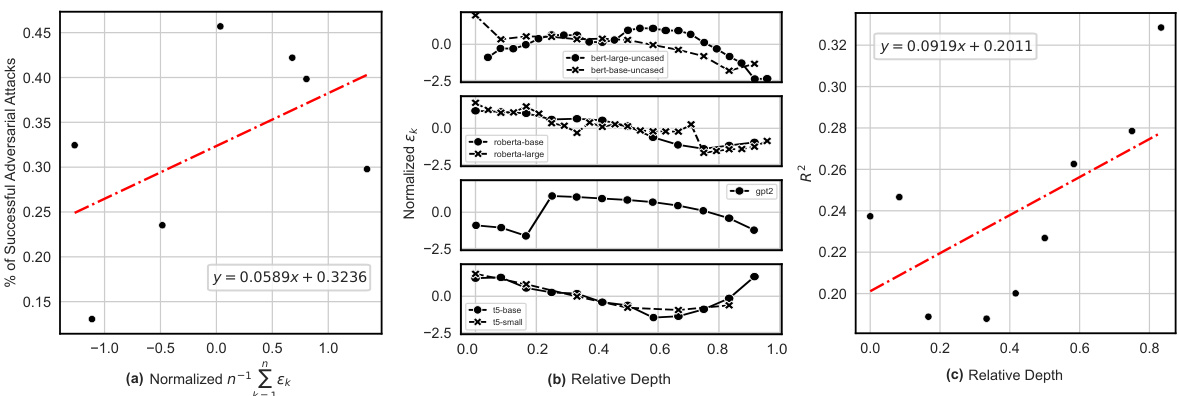
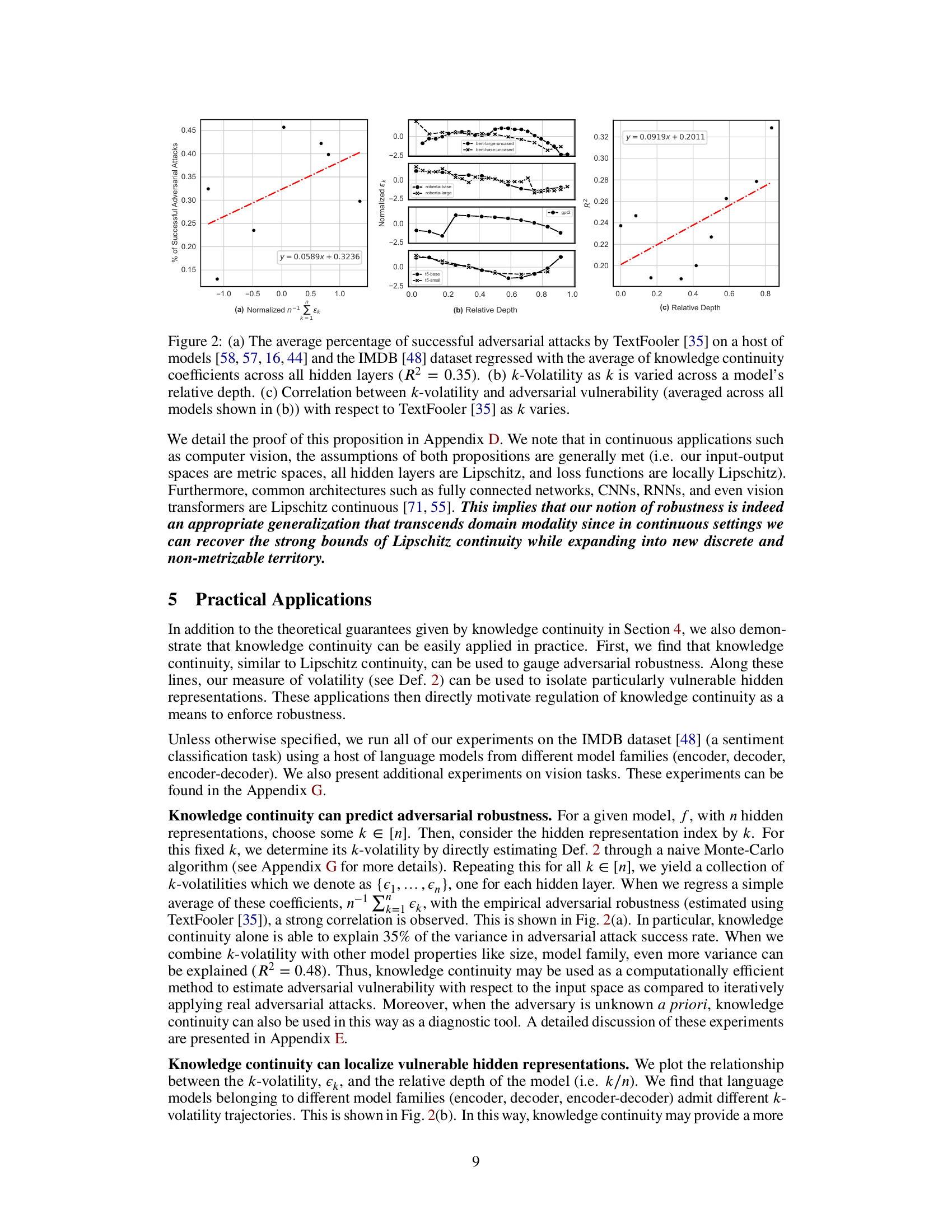
This figure demonstrates the correlation between knowledge continuity and adversarial robustness. Panel (a) shows a regression analysis indicating that the average knowledge continuity across hidden layers correlates with the percentage of successful adversarial attacks (R-squared = 0.35). Panels (b) and (c) further explore this relationship by showing how k-volatility (a measure of knowledge continuity at a specific layer) changes with the relative depth of the model and its correlation with adversarial vulnerability.

This figure illustrates three different scenarios regarding knowledge continuity in a model’s representation space. The first scenario shows sparse knowledge continuity, where a point (star) is isolated and has no nearby points with similar loss values. Any small perturbation would result in a large change in loss. The second case shows smooth knowledge continuity; points near a central point (star) have gradual changes in loss values, indicating continuity. The last case (circle) shows knowledge discontinuity; a point has a drastic change in loss value near it, indicating discontinuity. The key is that the classification (loss) is independent of the input and output spaces’ metrics (or lack thereof).
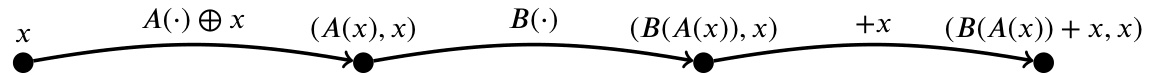
This figure illustrates three different scenarios regarding knowledge continuity in a model’s hidden representation space. The first scenario (★) shows sparse knowledge continuity, where a data point is isolated and far from similar points, leading to high volatility in loss with small changes in the representation. The second scenario (★) depicts knowledge continuity, where smooth changes in loss occur when the representation changes. Finally, the third scenario (●) displays knowledge discontinuity, showing that even a minor change in the representation leads to a large change in the loss function. The color of the points represents the loss values. Importantly, the visualization emphasizes that this classification is independent of any metric on the input/output spaces (X,Y).

This figure illustrates the concept of knowledge continuity using examples of sparse knowledge continuity, knowledge continuity, and knowledge discontinuity. It shows how the change in loss around a point in the hidden representation space relates to the concept of knowledge continuity. The color of the points represents loss, and their arrangement shows how the change in loss varies with respect to the closeness of the points in the hidden representation space. The lack of a metric on X and Y is emphasized, indicating the model’s knowledge is not dependent on input/output distance.
This figure shows the correlation between knowledge continuity and adversarial robustness. Panel (a) demonstrates a regression showing that the average knowledge continuity across hidden layers correlates with the success rate of adversarial attacks (TextFooler) on several language models using the IMDB dataset. Panel (b) illustrates how k-volatility (a measure of knowledge continuity) changes with the relative depth (layer number) of the model. Finally, panel (c) shows the correlation between k-volatility and the success rate of adversarial attacks for different layers in the models.
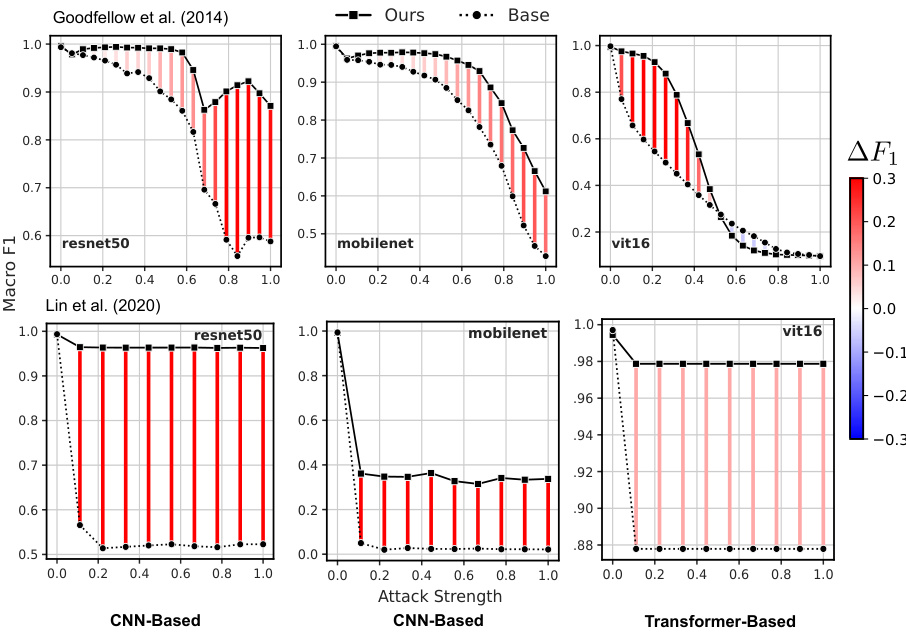
This figure shows the results of applying the knowledge continuity regularization method to various vision models. Two adversarial attacks, FGSM and SI-NI-FGSM, were used with varying strengths. The x-axis represents the attack strength, and the y-axis shows the macro F1 score. The top row shows results for the FGSM attack, while the bottom row displays results for the SI-NI-FGSM attack. The three columns show results for three different model architectures: ResNet50, MobileNet, and ViT16. The red bars represent the performance of the models with the knowledge continuity regularization applied, while the black dots represent the performance of the baseline models without regularization. The color scale shows the difference in macro F1 score between the regularized and baseline models.
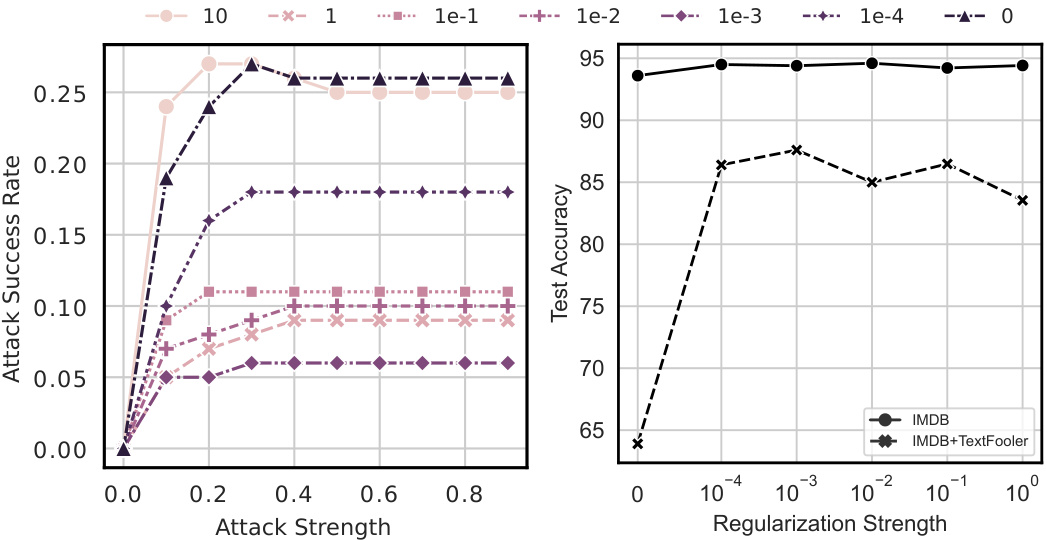
This figure shows the ablation study of the hyperparameters used in the knowledge continuity regularization algorithm. The left plot shows the attack success rate curves with different regularization strength (λ) for various attack strengths. The right plot shows test accuracy against regularization strength (λ) with fixed attack strength (0.3). It demonstrates that moderate regularization significantly improves robustness without sacrificing test accuracy.

This figure shows the results of applying a certification algorithm (Alg. 2) to a GPT-2 model, both before and after applying a knowledge continuity regularization (Alg. 1). The algorithm assesses the model’s robustness to perturbations. Each line represents a different threshold for considering examples as ’non-robust’. The y-axis indicates the certified probability that examples exceed this non-robustness threshold at a given perturbation distance (x-axis). The color gradient likely represents the change in model accuracy from the unperturbed baseline, showing how accuracy degrades with increasing perturbation magnitude.
More on tables
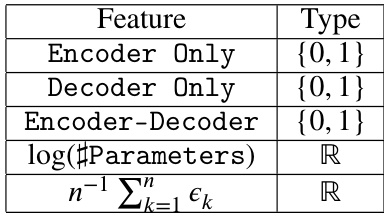
This table compares the performance of the proposed knowledge continuity regularization method against existing methods on various models and adversarial attacks. The results show that regulating knowledge continuity consistently improves robustness across different tasks and attacks.
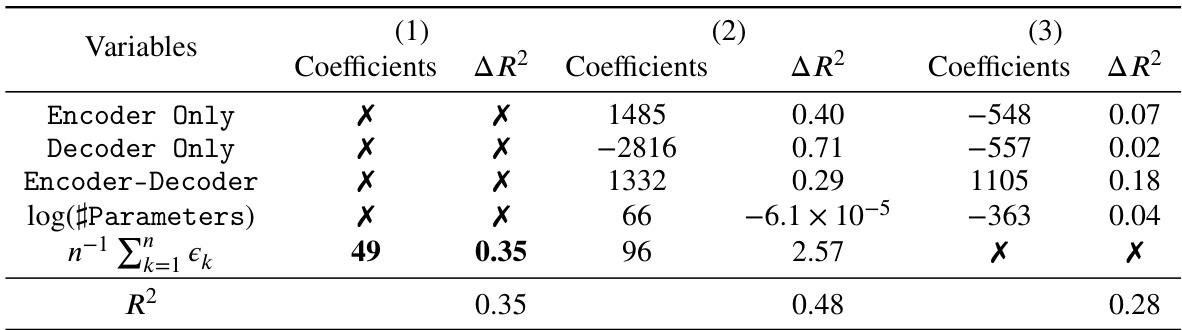
This table compares the performance of the proposed knowledge continuity regularization method against existing methods for various models and adversarial attacks. The results show that regulating knowledge continuity leads to improved robustness across a wide range of scenarios.
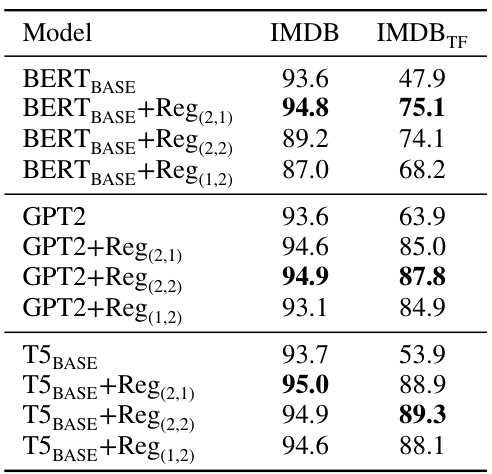
This table compares the performance of the proposed knowledge continuity regularization method against existing methods across various models and adversarial attacks on the IMDB dataset. It shows the accuracy of different models with and without the regularization, highlighting its effectiveness in improving robustness under adversarial attacks.
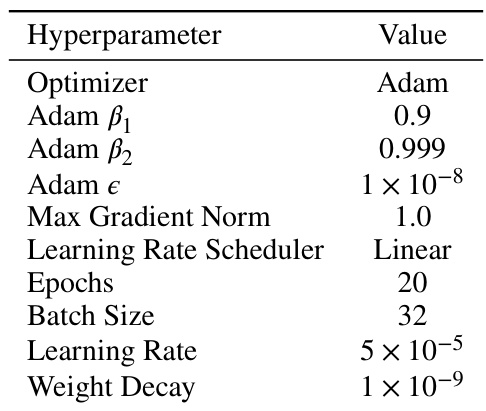
This table compares the performance of the proposed knowledge continuity regularization method against existing methods on various tasks and adversarial attacks. It shows that the proposed method generally achieves superior robustness across different model families and attack types.
Full paper#