Weight for Robustness: A Comprehensive Approach towards Optimal Fault-Tolerant Asynchronous ML

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in distributed machine learning, particularly those working on fault-tolerant systems. It offers a novel approach to asynchronous Byzantine-robust training, addressing a significant challenge in scaling ML to massive datasets and heterogeneous computing environments. The results could lead to more efficient and robust ML systems, and the methodology opens new avenues for research in variance reduction techniques and weighted aggregation strategies.

Visual Insights

#

The figure shows a timeline illustrating delays in asynchronous distributed systems. The timeline is divided into segments representing different update times from a worker (i). The green circles represent previous updates from worker i at time t − τ(i) and t(i). The blue circle represents the current time t. The thick black line at the bottom represents the delay τ(i) between the current update and the previous update from worker i.

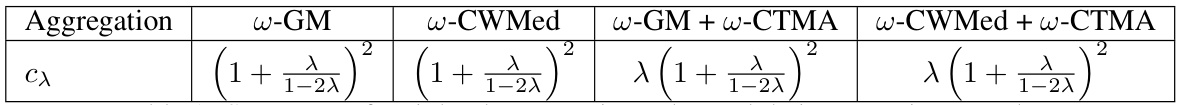
This table summarizes the theoretical guarantees for several weighted robust aggregation rules. The rules are designed to handle Byzantine failures in asynchronous distributed machine learning. The cx value quantifies the robustness of each aggregation rule in terms of how well it filters out the effect of Byzantine updates, with lower cx values being more robust.

In-depth insights

#

Async Byzantine ML

#

Asynchronous Byzantine Machine Learning (Async Byzantine ML) presents a unique set of challenges in distributed training. The inherent asynchronicity, where worker updates arrive at the parameter server at irregular intervals, complicates the detection and mitigation of Byzantine failures (malicious or faulty worker behavior). Unlike synchronous settings, delays obscure the impact of Byzantine updates, introducing additional bias and making it difficult to ensure convergence. Robust aggregation techniques, crucial for handling Byzantine faults in synchronous systems, must be adapted to account for the weighted influence of delayed updates. Weighted robust aggregators are developed to address the unequal contribution of workers based on their update frequency. Achieving optimal convergence rates in this environment necessitates innovative strategies that manage the effects of both asynchronicity and Byzantine behavior, such as variance reduction techniques. The need to utilize historical gradient information, successfully employed in synchronous Byzantine ML to reduce the impact of outliers, also takes on added complexity in asynchronous systems due to potentially stale information. Addressing these challenges leads to more robust and efficient large-scale machine learning systems that are resilient to various types of failures.

Weighted Aggregation

#

In the context of distributed machine learning, particularly when dealing with asynchronous systems and Byzantine failures, weighted aggregation emerges as a crucial technique. Standard aggregation methods, which treat all worker contributions equally, are insufficient in these scenarios. The inherent delays and potential for malicious behavior in asynchronous systems introduce bias that obscures disruptions. Therefore, weighted aggregation schemes, which assign weights to workers based on factors like update frequency or perceived trustworthiness, are necessary to mitigate the impact of these issues. The choice of weights is critical and depends on the specific challenges presented by the asynchronous and/or Byzantine environment. An effective weighting strategy enhances fault tolerance, leading to improved model accuracy and robustness. Robust aggregators, designed to filter out outliers, are often combined with weighted aggregation. The design of these weighted aggregators is an area of active research; finding weighting schemes that achieve optimal convergence rates while handling various failure scenarios remains a key challenge.

μ²-SGD Algorithm

#

The μ²-SGD algorithm is a novel approach to stochastic gradient descent that incorporates a double momentum mechanism to accelerate convergence and enhance variance reduction. It addresses the challenges of asynchronous training, particularly in the presence of Byzantine failures, by leveraging a weighted robust aggregation framework. This framework allows for the unequal weighting of gradient updates from different workers, mitigating the adverse effects of delays and malicious updates. The algorithm cleverly combines the unique features of double momentum, which uses a combination of past and present gradients, along with the robustness of weighted aggregation to produce an optimal convergence rate. This is a significant achievement as it tackles the combined problem of asynchronous communication and Byzantine faults that often plague distributed machine learning systems. Theoretical analysis demonstrates the superiority of μ²-SGD, showcasing a convergence rate that surpasses existing methods and is independent of the problem’s dimensionality. Empirical evaluations further support this finding, highlighting the robustness and efficiency of the proposed algorithm.

Optimal Convergence

#

The concept of ‘Optimal Convergence’ in the context of asynchronous Byzantine machine learning is crucial. It signifies achieving the fastest possible convergence rate to a solution while handling the challenges of both asynchronous updates and potential malicious behavior (Byzantine faults) from some workers. The authors’ claim to achieve this optimal rate is a significant contribution, as asynchronous systems are notoriously difficult to analyze and optimize due to the unpredictable delays and data inconsistencies. Their methodology, involving novel weighted robust aggregation and a variance-reduction technique (μ²-SGD), is designed to mitigate the effects of these delays and Byzantine failures. The key lies in the integration of weights into the aggregation process, which allows the system to adapt to the varying reliability and speed of different workers, giving more importance to more frequent updates. Optimal convergence is demonstrably shown empirically by outperforming non-weighted aggregators and other baselines in asynchronous Byzantine settings. This is backed by theoretical analysis establishing the optimal convergence rate, showcasing a major advance in making asynchronous Byzantine ML systems more efficient and robust.

Future Directions

#

Future research could explore extensions to non-convex settings, as the current work focuses on stochastic convex optimization. Investigating the impact of different robust aggregation techniques beyond those analyzed in the paper, and evaluating their performance under various asynchronous conditions, would be beneficial. A deeper dive into the practical implications of weighted aggregation in diverse distributed machine learning scenarios is warranted. Additionally, analyzing the algorithm’s sensitivity to various Byzantine attack strategies and developing more resilient mechanisms is crucial. Finally, a thorough examination of the trade-offs between convergence speed, communication overhead, and computational cost in different asynchronous Byzantine environments would provide valuable insights for real-world applications.

More visual insights

#

More on figures

This figure compares the test accuracy of weighted and non-weighted robust aggregators on the MNIST dataset in an asynchronous Byzantine setting. The experiment uses 17 workers, 8 of which are Byzantine, and simulates a scenario where faster workers send updates more frequently (arrival probability proportional to the square of their ID). The comparison is shown for two types of Byzantine attacks: label flipping (left) and sign flipping (right). The results illustrate that weighted robust aggregators generally perform better than their non-weighted counterparts.

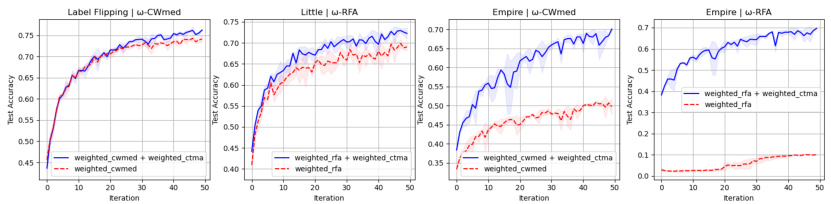
This figure compares the test accuracy of weighted robust aggregators (w-CWMed and w-RFA) with and without the w-CTMA meta-aggregator under different Byzantine attack scenarios in MNIST dataset. The scenarios include sign flipping and attacks named ’little’ and ’empire’, which differ in their characteristics and aggressiveness. The results show that incorporating w-CTMA enhances the accuracy, especially in challenging scenarios like the ’empire’ attack. The x-axis represents the number of iterations, and the y-axis shows the test accuracy.

This figure compares the performance of three different optimizers (μ²-SGD, standard momentum, and SGD) on the CIFAR-10 dataset in an asynchronous Byzantine setting. The results show that μ²-SGD performs similarly to standard momentum, while SGD performs significantly worse. The experiment simulates 9 workers, with 4 of them being Byzantine (malicious or faulty). The fraction of Byzantine updates is set at λ = 0.4 for the first three scenarios, and λ = 0.3 for the label flipping attack. Worker arrival probabilities are proportional to their ID, leading to an imbalanced asynchronous setting. The results highlight the importance of using more advanced algorithms like μ²-SGD, which leverage historical information, for robust performance in asynchronous Byzantine settings.

This figure compares the test accuracy of weighted and non-weighted robust aggregators on the MNIST dataset in an asynchronous Byzantine setting. The experiment uses 17 workers (8 Byzantine), with faster workers having a higher chance of contributing updates. Two attack types are shown: label flipping (left) and sign flipping (right), with different fractions of Byzantine updates (λ). The results demonstrate that weighted robust aggregators consistently outperform their non-weighted counterparts.

This figure compares the performance of weighted robust aggregators (w-CWMed and w-RFA) with and without the addition of the w-CTMA meta-aggregator under different Byzantine attack scenarios in the MNIST dataset. The attacks simulated are sign flipping, little, and empire. The results show that w-CTMA improves robustness, particularly in more challenging attack scenarios like the empire attack.

This figure compares the performance of three different optimizers: μ²-SGD, standard momentum (with β=0.8 and β=0.9), and standard SGD in an asynchronous Byzantine setting on the MNIST dataset. The experiment setup includes 9 workers with 4 Byzantine workers (λ=0.4), and workers’ arrival probabilities are proportional to their IDs. The figure shows that μ²-SGD achieves comparable performance to momentum while significantly outperforming standard SGD, highlighting the importance of incorporating historical information when addressing Byzantine scenarios.

More on tables

This table summarizes the values of the parameter cx for several weighted robust aggregation rules. The parameter cx is a crucial element in determining the robustness of the aggregation rules against Byzantine failures. Lower values of cx imply greater robustness. The table includes weighted versions of the Geometric Median (w-GM), Coordinate-Wise Median (w-CWMed), and their combinations with the Weighted Centered Trimmed Meta Aggregator (w-CTMA).

This table summarizes the experimental setup used in the paper for both the MNIST and CIFAR-10 datasets. It details the model architecture (including convolutional and fully connected layers, activation functions, and batch normalization), learning rate, batch size, and data pre-processing and augmentation techniques (normalization and random transformations). The specifics are tailored to each dataset to optimize performance.

Full paper

#