TL;DR#
Stochastic second-order optimization methods are attractive for solving large-scale machine learning problems because they offer faster convergence rates than first-order methods. However, they often suffer from slow global convergence and high per-iteration costs. The method presented in [1] improved this by using a Hessian averaging scheme; however, it still suffered from slow global convergence.
This paper introduces a novel method called Stochastic Newton Proximal Extragradient (SNPE) that overcomes the limitations of existing methods. SNPE achieves a faster global convergence rate and reaches the same superlinear rate in significantly fewer iterations than existing methods. This improvement is achieved by extending the Hybrid Proximal Extragradient (HPE) framework, allowing for faster transitions between convergence phases. The results are supported by both theoretical analysis and numerical experiments.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on stochastic optimization, particularly those focusing on second-order methods. It offers significant improvements in convergence rates and computational efficiency, opening new avenues for large-scale machine learning applications and impacting fields relying on large datasets. The introduction of the hybrid proximal extragradient framework provides a novel and potentially more broadly applicable approach.
Visual Insights#
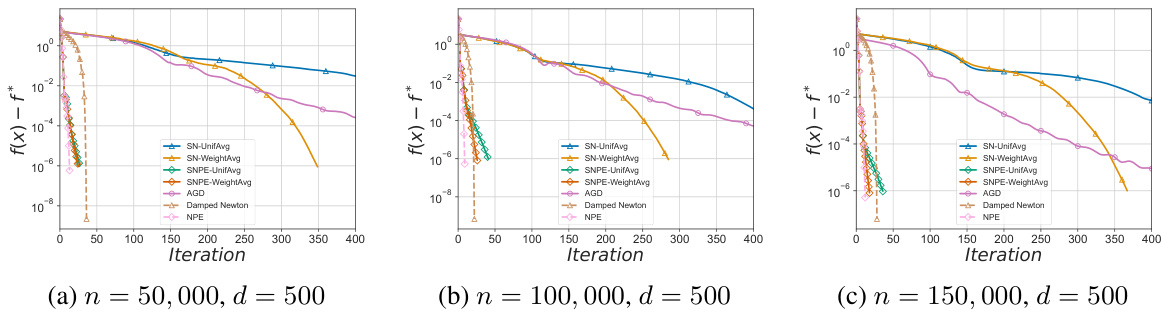
🔼 The figure shows the iteration complexity comparison for minimizing the regularized log-sum-exp objective function on a synthetic dataset. Different optimization methods are compared: Stochastic Newton with uniform averaging, Stochastic Newton with weighted averaging, SNPE (Stochastic Newton Proximal Extragradient) with uniform averaging, SNPE with weighted averaging, Accelerated Gradient Descent (AGD), Damped Newton, and Newton Proximal Extragradient (NPE). The x-axis represents the number of iterations, and the y-axis represents the difference between the objective function value and its optimal value (f(x) - f*). The results are shown for three different dataset sizes (n = 50,000, 100,000, and 150,000, with d = 500 in all cases). The figure demonstrates the convergence behavior of various methods, highlighting the relative performance of SNPE compared to other methods in terms of convergence speed.
read the caption
Figure 1: Iteration complexity comparison for minimizing log-sum-exp on a synthetic dataset.

🔼 This table compares the performance of the proposed Stochastic Newton Proximal Extragradient (SNPE) method (Algorithm 1) with the stochastic Newton method from a previous work [1] in terms of the number of iterations required to reach different convergence phases (linear, initial superlinear, and final superlinear) and the corresponding convergence rates. It shows that SNPE requires significantly fewer iterations to transition between phases and achieves faster convergence rates, particularly in the initial superlinear phase. The comparison is made for both uniform and non-uniform weight averaging schemes for Hessian estimates.
read the caption
Table 1: Comparison between Algorithm 1 and the stochastic Newton method in [1], in terms of how many iterations it takes to transition to each phase, and the convergence rates achieved. We drop constant factors as well as logarithmic dependence and 1/8, and assume 1/poly(κ) < γ < O(κ).
In-depth insights#
SNPE: Core Concept#
The core concept of Stochastic Newton Proximal Extragradient (SNPE) lies in its innovative integration of second-order information with the Hybrid Proximal Extragradient (HPE) framework. Unlike traditional stochastic Newton methods that suffer from slow global convergence due to diminishing stochastic Hessian noise, SNPE cleverly employs a weighted averaging scheme for Hessian approximations. This significantly reduces noise while maintaining computational efficiency, leading to faster convergence rates. The method leverages the HPE framework’s strength in global convergence, combining it with the local quadratic convergence speed of Newton’s method. By carefully managing inexact proximal point updates through a line search mechanism, SNPE achieves a fast global linear rate and a superlinear local convergence rate, thereby outperforming existing methods in both global and local convergence behavior. The use of weighted averaging for the Hessian is a crucial aspect. It allows SNPE to balance the trade-off between bias and variance in Hessian estimates, offering superior performance over uniform averaging strategies.
Hessian Averaging#
Hessian averaging is a crucial technique in stochastic Newton-type methods for optimization. It addresses the challenge of noisy Hessian estimations by combining multiple noisy Hessian approximations, effectively reducing the variance and improving the quality of the Hessian information used in the optimization process. The averaging scheme, whether uniform or weighted, plays a significant role in balancing bias and variance. Uniform averaging is simpler but may converge slower, while weighted averaging, which assigns more weight to recent Hessian estimates, offers faster convergence but introduces more complexity. The choice of averaging scheme and its parameters is key in determining the trade-off between computational cost and convergence speed. The core idea is to leverage past information to better estimate the true Hessian, thereby enhancing the performance and stability of stochastic Newton methods. Effectively mitigating the adverse effects of noisy Hessian approximations is crucial to ensuring efficient and accurate optimization, especially in large-scale machine learning problems where exact Hessian computation is prohibitively expensive. Therefore, careful consideration and analysis of Hessian averaging are critical to optimize the overall efficiency and effectiveness of the algorithm.
Convergence Rates#
The analysis of convergence rates for stochastic Newton methods is multifaceted, involving distinct phases with varying rates. Initially, a warm-up phase exists where convergence is slow due to high noise in the stochastic Hessian approximations. This transitions to a linear convergence phase with a rate dependent on the condition number (κ) and noise level (Υ). Notably, the method’s ability to achieve a superlinear convergence rate is a key focus, typically characterized by a transition from a slower to a faster superlinear rate. The number of iterations required to reach these different phases significantly impacts the overall computational complexity and is heavily influenced by the averaging scheme used for the stochastic Hessian estimates. The use of uniform versus weighted averaging strategies notably impacts these transition points. Weighted averaging often proves more efficient, accelerating convergence and reducing the iterations needed to achieve both linear and superlinear rates.
Computational Cost#
Analyzing the computational cost of a stochastic Newton method reveals a complex interplay of factors. Gradient computation, typically O(nd), is often significantly cheaper than Hessian computation, which can be O(nd²) or even O(n³). Stochastic methods aim to mitigate this by using subsampling or sketching to approximate the Hessian, lowering the cost to O(sd²) where s « n. However, this introduces noise, impacting convergence rate and iteration count. Averaging techniques, like those used in the paper, trade off bias and variance, improving convergence but also potentially increasing per-iteration costs. The paper cleverly analyzes the trade-offs by considering the convergence rate, global vs. local convergence and the cost of achieving superlinear convergence. The choice of averaging scheme, uniform or weighted, significantly influences the overall efficiency, affecting both iteration count and the transition points to superlinear regimes. Therefore, a comprehensive cost analysis must integrate per-iteration computational cost with the number of iterations required to reach a desired accuracy, making a direct comparison to deterministic methods challenging.
Future Work#
The paper’s focus on strongly convex functions presents a natural avenue for future work involving the extension to the more general class of convex functions. This would significantly broaden the applicability of the proposed stochastic Newton proximal extragradient method (SNPE). Addressing the non-convex setting is also crucial, potentially leveraging techniques like curvature approximations or line searches tailored to such scenarios. Another promising area is improving the Hessian approximation strategies to reduce bias and variance, perhaps by incorporating adaptive sampling or advanced sketching techniques. The current analysis relies on the assumption of a positive semi-definite Hessian approximation; relaxing this assumption could enhance practicality. Finally, empirical evaluation on diverse large-scale machine learning tasks, alongside a detailed comparison with state-of-the-art methods, would strengthen the paper’s impact and showcase SNPE’s practical performance.
More visual insights#
More on figures

🔼 The figure shows the iteration complexity comparison for minimizing the regularized log-sum-exp function on three synthetic datasets with varying sample sizes (n = 50,000, 100,000, and 150,000) and dimension (d = 500). It compares the performance of several algorithms, including Stochastic Newton with uniform and weighted Hessian averaging (SN-UnifAvg, SN-WeightAvg), Stochastic Newton Proximal Extragradient (SNPE) with uniform and weighted Hessian averaging (SNPE-UnifAvg, SNPE-WeightAvg), Accelerated Gradient Descent (AGD), Damped Newton, and Newton Proximal Extragradient (NPE). The y-axis represents the value of f(x) - f*, where f* is the optimal value, showing the convergence progress of the algorithms over iterations (x-axis). The plot demonstrates that SNPE methods converge faster than other methods, especially in later iterations.
read the caption
Figure 1: Iteration complexity comparison for minimizing log-sum-exp on a synthetic dataset.

🔼 This figure compares the performance of the Stochastic Newton Proximal Extragradient (SNPE) method with and without the extragradient step. The results show that removing the extragradient step generally leads to faster convergence for all three datasets (n=50,000, 100,000, and 150,000 with d=500). The SNPE method with the extragradient step still outperforms the Stochastic Newton method from [1].
read the caption
Figure 3: The effect of the extragradient step in stochastic NPE.
More on tables

🔼 This table compares the number of iterations required to reach different convergence phases (linear, initial superlinear, and final superlinear) for Algorithm 1 (Stochastic NPE) and the stochastic Newton method from a previous work [1]. It shows how the convergence rates differ between the two methods under both uniform and non-uniform Hessian averaging schemes. The table highlights the improved iteration complexity of Algorithm 1, particularly in transitioning to the superlinear convergence phases.
read the caption
Table 1: Comparison between Algorithm 1 and the stochastic Newton method in [1], in terms of how many iterations it takes to transition to each phase, and the convergence rates achieved. We drop constant factors as well as logarithmic dependence and 1/8, and assume 1/poly(κ) < Y < O(κ).

🔼 The table compares the number of iterations required to reach different convergence phases (linear, initial superlinear, and final superlinear) for Algorithm 1 (the proposed Stochastic Newton Proximal Extragradient method) and the stochastic Newton method from a previous work [1]. It shows how the convergence rates and the number of iterations needed to transition between phases depend on the condition number (κ) and the noise level (Y) for both methods, using different weighting schemes (uniform and non-uniform).
read the caption
Table 1: Comparison between Algorithm 1 and the stochastic Newton method in [1], in terms of how many iterations it takes to transition to each phase, and the convergence rates achieved. We drop constant factors as well as logarithmic dependence and 1/8, and assume 1/poly(κ) < Y < O(κ).
Full paper#



















