↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many machine learning applications involve bilevel optimization problems. However, existing algorithms struggle with problems where the upper-level function’s smoothness is unbounded—meaning its smoothness constant scales with the gradient norm, lacking a uniform upper bound. This makes finding an approximate solution (within a certain error tolerance) computationally expensive, limiting their applicability to large-scale problems.
This paper introduces AccBO, a novel algorithm designed to tackle this challenge. AccBO achieves a significantly improved convergence rate (O(ε⁻³)) compared to the state-of-the-art (O(ε⁻⁴)). This improvement stems from its use of normalized stochastic gradient descent with recursive momentum for the upper-level and stochastic Nesterov accelerated gradient descent for the lower-level variables. The improved algorithm is rigorously analyzed and shown to provide the predicted theoretical speedup through experiments on various machine learning problems.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in bilevel optimization and related machine learning fields. It addresses a significant limitation of existing methods by handling unbounded smoothness in nonconvex upper-level problems. The improved oracle complexity of O(ε⁻³) offers a substantial efficiency gain, making it relevant for large-scale applications. The novel algorithmic techniques and theoretical analysis open doors for developing more efficient and scalable bilevel optimization algorithms.
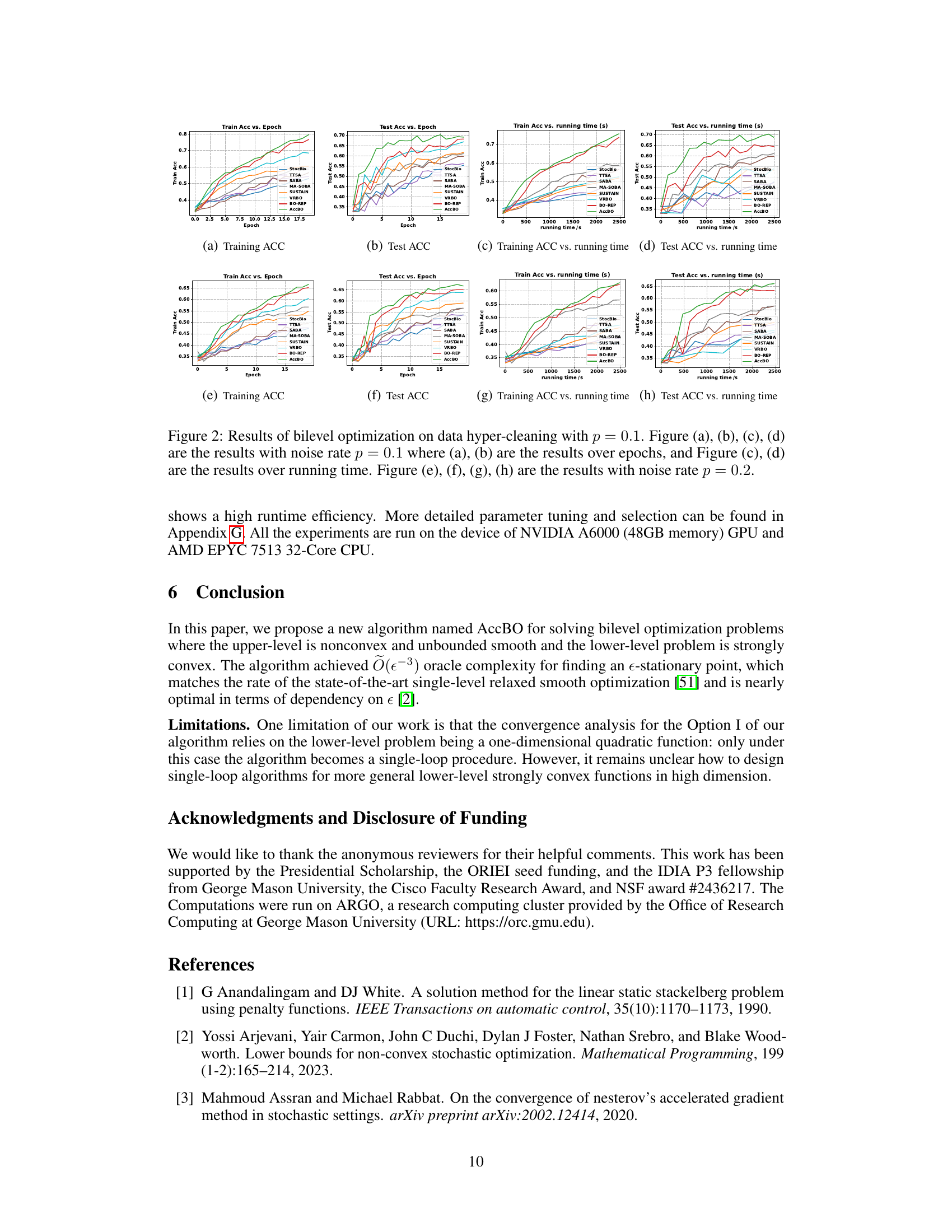
Visual Insights#

This figure presents the results of applying bilevel optimization algorithms to a deep AUC maximization task. Subfigures (a) and (b) display the training and test AUC scores, respectively, plotted against the number of training epochs. Subfigures (c) and (d) show the same metrics but plotted against the running time of the algorithms. The figure compares the performance of the proposed AccBO algorithm against several baselines, including StocBio, TTSA, SABA, MA-SOBA, SUSTAIN, VRBO, and BO-REP. The results demonstrate that AccBO achieves higher AUC scores and faster convergence than the other methods.

This algorithm details the steps of the Stochastic Nesterov Accelerated Gradient Method, which is a crucial subroutine used within the AccBO algorithm for updating the lower-level variable. It leverages momentum to accelerate convergence towards the optimal solution of the lower-level problem, given a fixed upper-level variable. The algorithm iteratively updates the lower-level variable using stochastic gradient information, incorporating momentum from previous iterations. It’s an adaptation of the Nesterov Accelerated Gradient method to handle stochasticity.
Full paper#