TL;DR#
Distributionally Robust Optimization (DRO) aims to improve model performance by considering uncertainty in data distributions. However, traditional DRO methods struggle when dealing with datasets contaminated by outliers; these outliers can significantly skew the results. Existing methods, like those relying on the Wasserstein distance, are especially sensitive to outliers.
This paper introduces a novel DRO framework that leverages unbalanced optimal transport (UOT) to mitigate the effect of outliers. Instead of using hard constraints to define the ambiguity set (as in traditional WDRO), UOT uses a soft penalization term, which is more resilient to outliers. The authors establish strong duality for their proposed method and its Lagrangian penalty formulation, showcasing theoretical rigor. They also demonstrate the computational benefits of their approach, making it suitable for large datasets.
Key Takeaways#
Why does it matter?#
This paper is important because it offers a novel and efficient solution to the challenging problem of outlier robustness in distributionally robust optimization (DRO). The proposed method, using unbalanced optimal transport, provides improved robustness to outliers while maintaining computational efficiency, making it highly relevant for large-scale machine learning applications. This work opens new avenues for research in DRO, particularly in handling contaminated data, and contributes significantly to the development of more reliable and practical DRO algorithms.
Visual Insights#

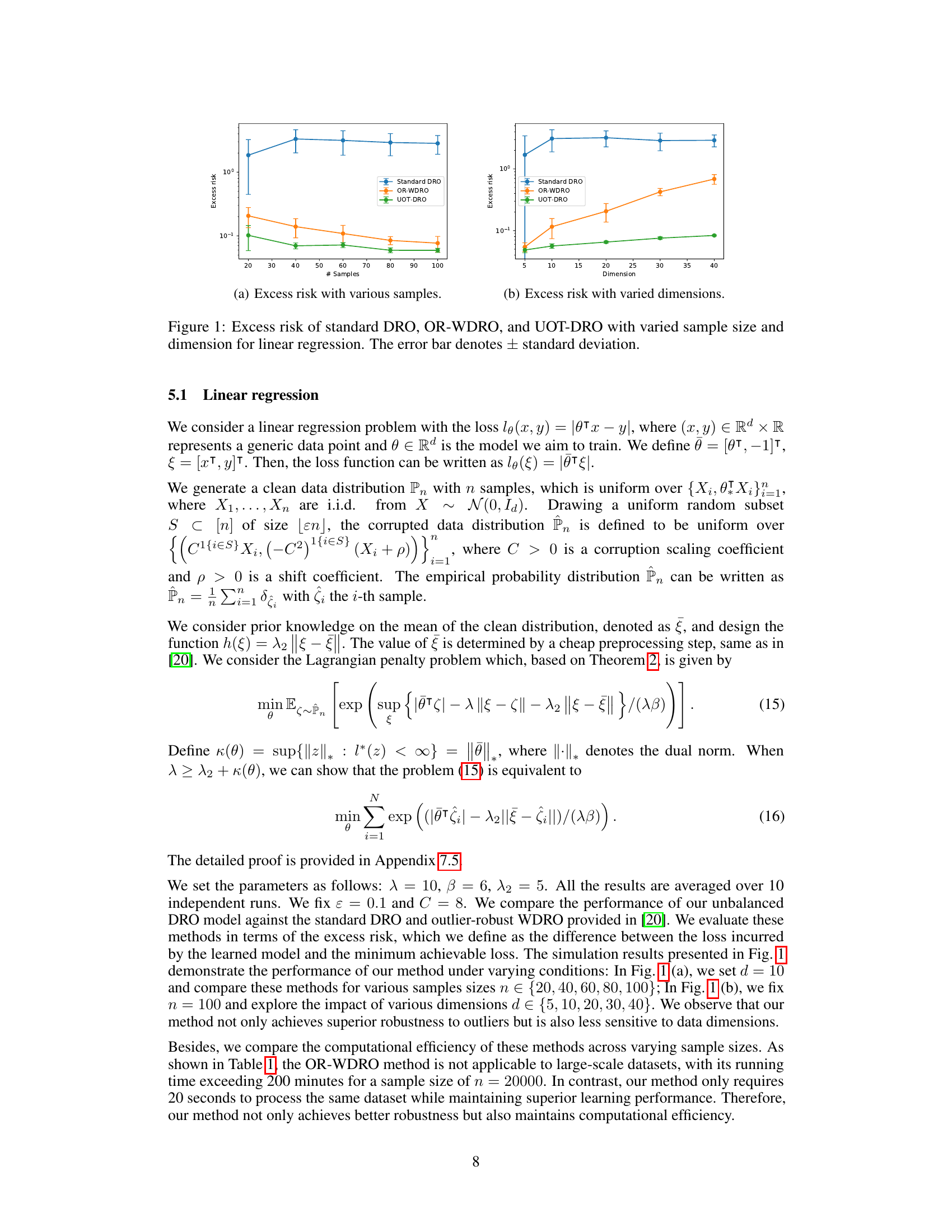
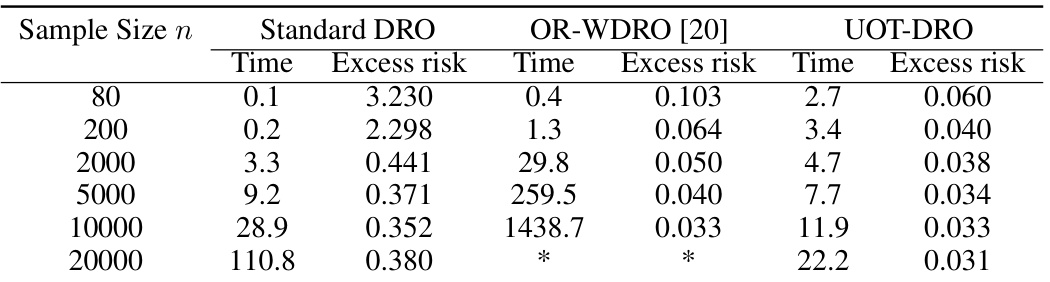
🔼 This figure compares the excess risk (difference between obtained loss and the minimum achievable loss) of three different distributionally robust optimization (DRO) methods: standard DRO, outlier-robust WDRO, and the proposed UOT-DRO. The comparison is done across varying sample sizes (Figure 1a) and dimensions (Figure 1b) in a linear regression setting. UOT-DRO consistently shows lower excess risk across different sample sizes and dimensions, indicating superior robustness and less sensitivity to data dimensionality, especially compared to the standard DRO method.
read the caption
Figure 1: Excess risk of standard DRO, OR-WDRO, and UOT-DRO with varied sample size and dimension for linear regression. The error bar denotes ± standard deviation.
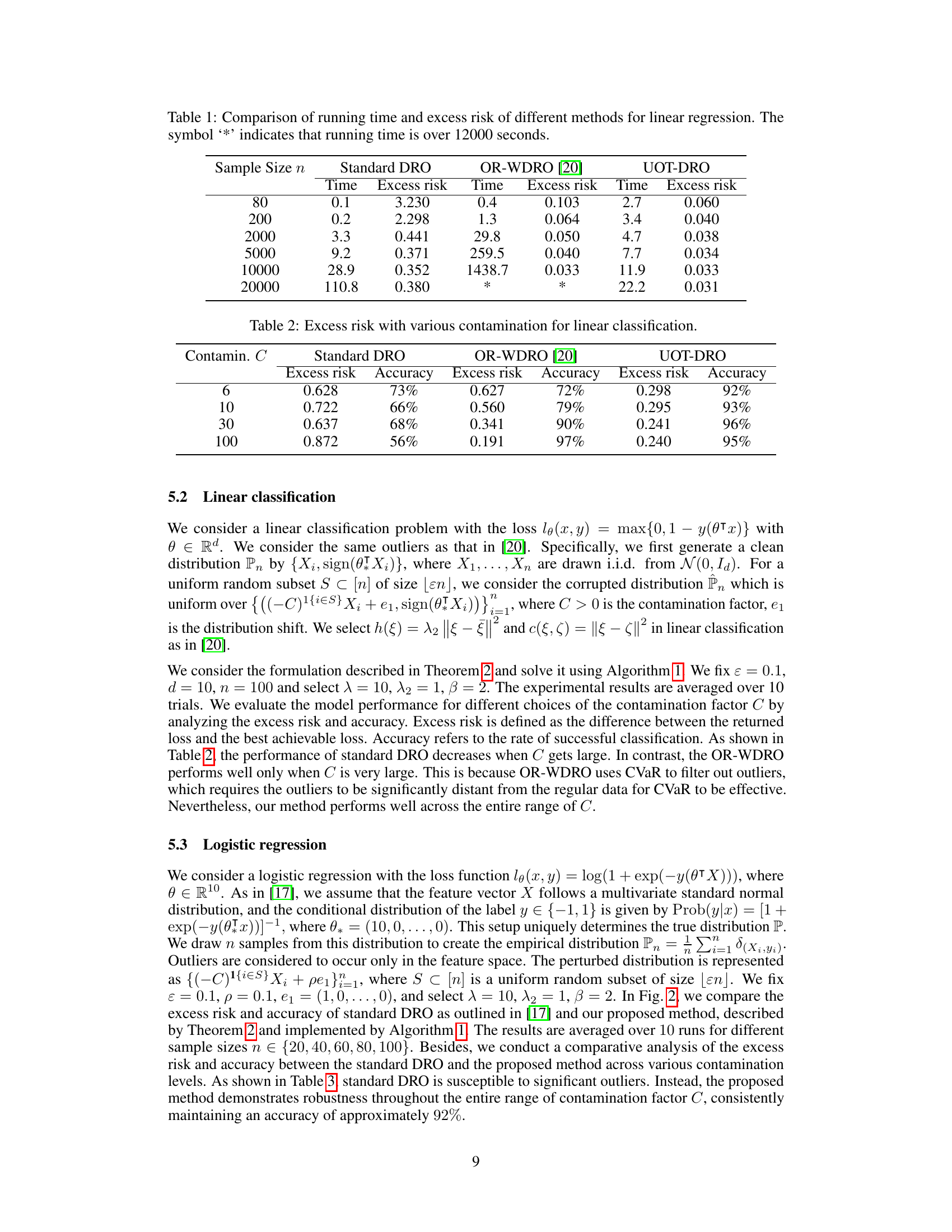
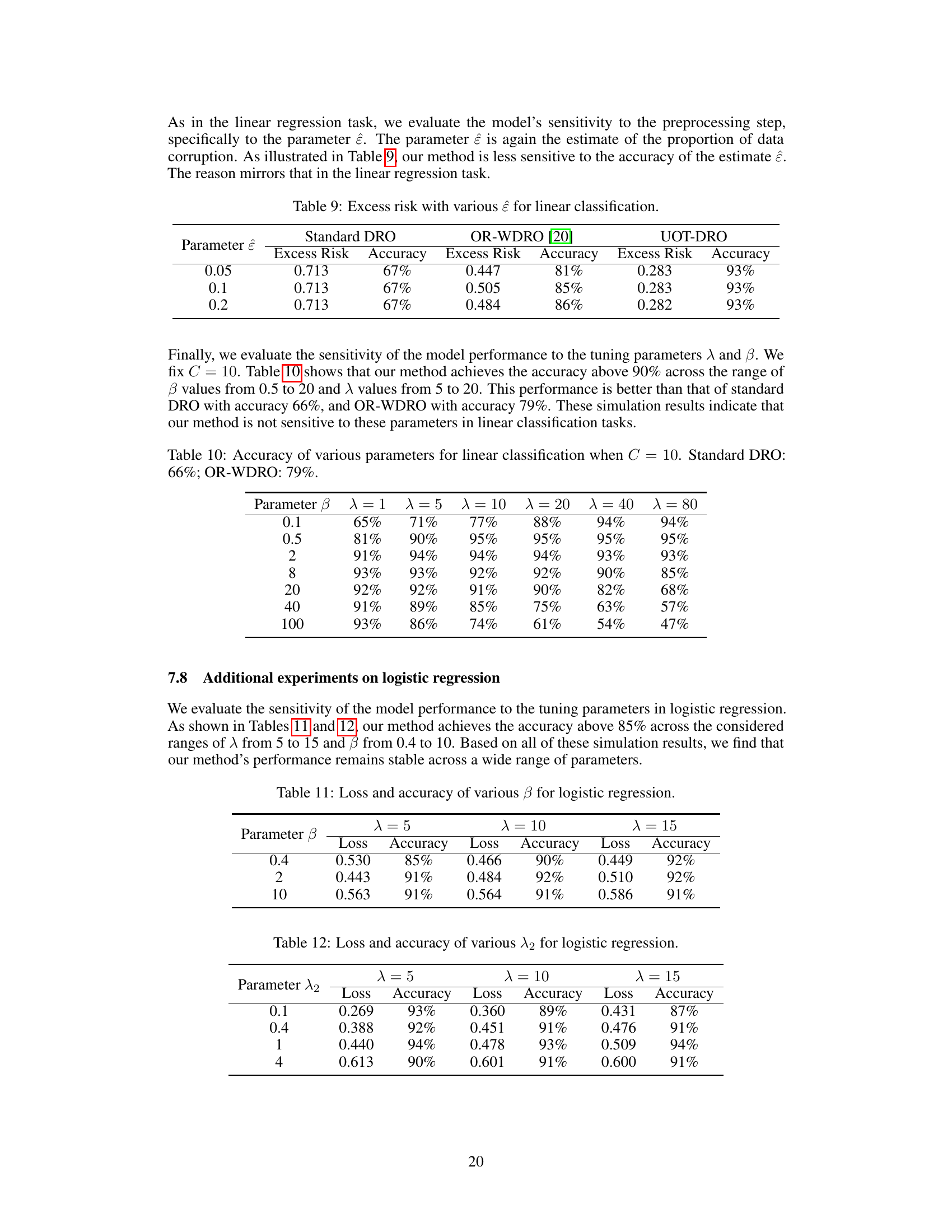
🔼 This table compares the computational efficiency and prediction accuracy of three different methods for linear regression: Standard DRO, OR-WDRO, and UOT-DRO. The comparison is made across six different sample sizes (80, 200, 2000, 5000, 10000, 20000). For each method and sample size, the table shows the running time (in seconds) and the excess risk (a measure of prediction error). The asterisk (*) indicates that the running time exceeded 12000 seconds, highlighting the computational advantages of the UOT-DRO method, especially for larger datasets.
read the caption
Table 1: Comparison of running time and excess risk of different methods for linear regression. The symbol '*' indicates that running time is over 12000 seconds.
In-depth insights#
UOT DRO#
The proposed “UOT DRO” framework offers a novel approach to distributionally robust optimization (DRO) by leveraging unbalanced optimal transport (UOT). This method addresses the limitations of traditional DRO, which struggles with outlier-contaminated datasets. Unlike standard DRO that uses hard constraints, UOT DRO employs a soft penalization term, resulting in an ambiguity set more resilient to outliers. This makes the UOT DRO approach more suitable for real-world applications with noisy data. The theoretical analysis establishes strong duality under smoothness conditions for both the original DRO problem and its computationally efficient Lagrangian penalty formulation. The resulting algorithm is computationally less demanding than traditional WDRO methods, enabling scalability to larger datasets. Empirical evidence from regression and classification tasks highlights improved robustness to outliers and enhanced computational efficiency. The combination of UOT’s outlier robustness with the theoretical guarantees of DRO positions UOT DRO as a promising technique for enhancing the reliability and practical applicability of DRO models.
Outlier Robustness#
The paper investigates enhancing the robustness of distributionally robust optimization (DRO) models to outliers. Existing DRO methods often struggle with outliers as they significantly affect the Wasserstein distance used in defining ambiguity sets. The proposed approach leverages unbalanced optimal transport (UOT), introducing a soft penalty term instead of hard constraints. This allows the model to be more resilient to outliers by effectively down-weighting their influence. The paper proves strong duality results for the UOT-based DRO formulation, offering theoretical guarantees for its performance. The resulting Lagrangian penalty formulation provides a computationally efficient algorithm suitable for large datasets. Experimental results show that this UOT-DRO approach provides improved robustness to outliers compared to traditional DRO methods and outlier-robust WDRO, while maintaining computational efficiency. This is particularly beneficial for real-world applications where data may contain significant outliers that could negatively bias the model’s performance. The method’s effectiveness is demonstrated across various regression and classification tasks, showing consistent improvements in out-of-sample performance.
Strong Duality#
Strong duality is a crucial concept in optimization, bridging the gap between primal and dual problems. It asserts that the optimal values of both problems are equal, which is incredibly valuable for several reasons. First, it offers an alternative way to solve a complex primal problem by tackling its often simpler dual counterpart. Second, strong duality provides valuable insights into the problem’s structure, revealing relationships between its constraints and objectives. The presence of strong duality also allows for the development of efficient algorithms exploiting the equivalence between primal and dual optimal solutions. However, strong duality is not guaranteed for all optimization problems, and its existence often depends on specific conditions such as convexity of the objective function and the feasibility of the problem. The paper’s exploration of strong duality in the context of unbalanced optimal transport demonstrates its relevance in robust optimization when dealing with data distributions affected by outliers. The theoretical results on strong duality establish a firm foundation for the proposed method’s computational efficiency and robustness to outliers.
Lagrangian Penalty#
The Lagrangian penalty method offers a computationally tractable approach to solving distributionally robust optimization (DRO) problems, particularly those involving the unbalanced Wasserstein distance. It addresses the challenge of strong duality, which is often difficult to establish and computationally expensive to solve in the original DRO formulation. By introducing a penalty term related to the unbalanced Wasserstein distance, this method provides strong duality guarantees under relaxed assumptions, making it more amenable to practical applications. The resulting dual problem allows for an efficient algorithm, such as the stochastic subgradient method, enabling the handling of large-scale datasets. This technique effectively reweights data points, mitigating the impact of outliers by using an exponential weighting scheme in the dual objective function. This approach balances robustness to outliers with computational tractability, making it a significant improvement over more traditional DRO methods that struggle with outliers and computational efficiency, particularly in the context of high-dimensional data.
Empirical Results#
An effective ‘Empirical Results’ section in a research paper would systematically present findings, comparing the proposed method (e.g., UOT-DRO) against established baselines (Standard DRO, OR-WDRO). Key metrics, such as excess risk and accuracy, should be reported across various experimental settings (sample size, dimensionality, contamination levels). The results should clearly demonstrate the superiority of the proposed method, especially in handling outliers and maintaining efficiency with large datasets. Visualizations, like plots showcasing excess risk across different sample sizes or dimensions, would strengthen the presentation. Crucially, the discussion should go beyond mere reporting to analyze the observed trends and provide insightful interpretations of why the proposed method performs better under specific conditions. Statistical significance should be addressed, justifying the claims about improved robustness and efficiency. Finally, the section should acknowledge any limitations of the empirical evaluation, for example, the chosen datasets or hyperparameters, ensuring an honest and balanced assessment of the method’s performance.
More visual insights#
More on figures
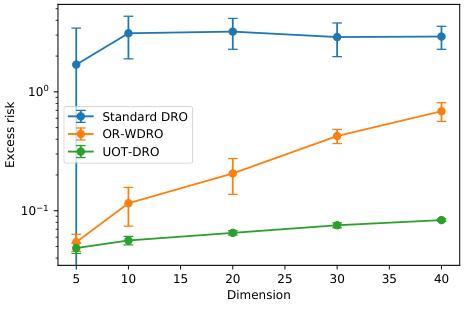
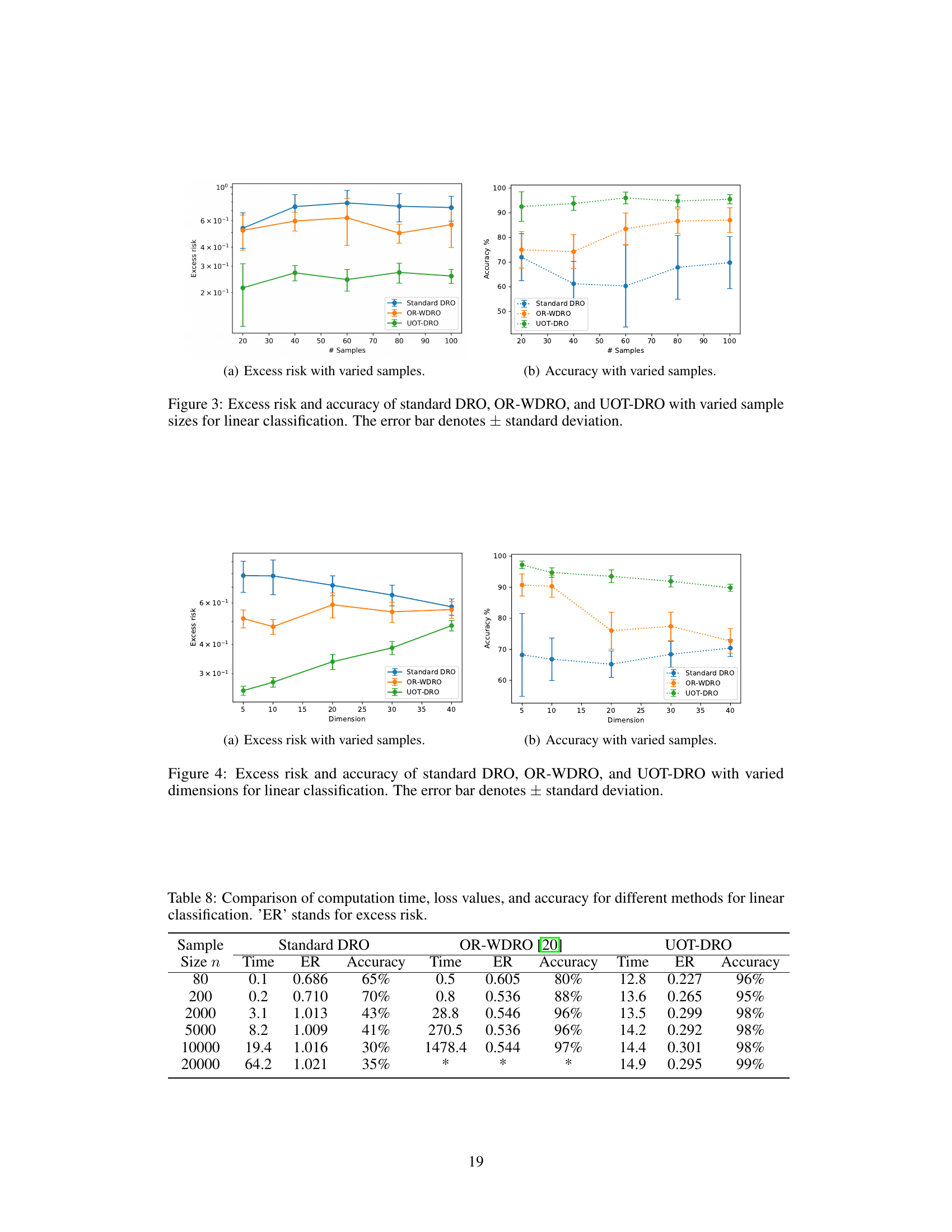
🔼 This figure compares the performance of three different distributionally robust optimization (DRO) methods for linear classification tasks across various dimensions. The x-axis represents the dimensionality of the data, and the y-axis shows the excess risk (the difference between the achieved loss and the minimum possible loss). The plot includes error bars indicating the standard deviation of the results. The figure helps illustrate how each DRO method handles varying dimensional data, allowing readers to assess the robustness of each approach in high-dimensional settings.
read the caption
Figure 4: Excess risk and accuracy of standard DRO, OR-WDRO, and UOT-DRO with varied dimensions for linear classification. The error bar denotes ± standard deviation.

🔼 This figure displays the performance comparison of standard DRO and the proposed UOT-DRO method on logistic regression tasks. The left panel shows the excess risk (the difference between the achieved loss and the minimum possible loss) for different sample sizes. The right panel shows the accuracy for different sample sizes. Both panels include error bars, representing the standard deviation across multiple trials, to illustrate the variability of the results.
read the caption
Figure 2: Excess risk and accuracy of standard DRO and UOT-DRO with varied sample sizes for logistic regression. The error bar denotes ± standard deviation.

🔼 This figure presents the excess risk (difference between the model’s loss and the minimum achievable loss) for linear regression using three different methods: standard DRO, OR-WDRO (outlier-robust Wasserstein DRO), and the proposed UOT-DRO method. The experiment is conducted with varying sample sizes (Figure 1a) and dimensions (Figure 1b) of the dataset, showcasing the robustness and efficiency of UOT-DRO in handling outliers and different data properties. The error bars show the standard deviation.
read the caption
Figure 1: Excess risk of standard DRO, OR-WDRO, and UOT-DRO with varied sample size and dimension for linear regression. The error bar denotes ± standard deviation.
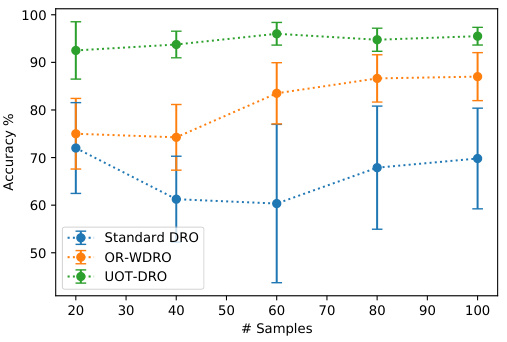
🔼 This figure compares the performance of three different distributionally robust optimization (DRO) methods - standard DRO, outlier-robust WDRO (OR-WDRO), and the proposed UOT-DRO - on a linear classification task. The x-axis represents the number of samples used for training, and the y-axis shows the excess risk (difference between the achieved loss and the minimum possible loss) and the accuracy. Error bars indicate the standard deviation, showing variability in the results. The plot demonstrates how the proposed UOT-DRO method achieves higher accuracy with increased sample sizes and outperforms the other methods in terms of excess risk.
read the caption
Figure 3: Excess risk and accuracy of standard DRO, OR-WDRO, and UOT-DRO with varied sample sizes for linear classification. The error bar denotes ± standard deviation.

🔼 This figure compares the performance of three different distributionally robust optimization (DRO) methods – Standard DRO, OR-WDRO, and UOT-DRO – in linear classification tasks, specifically focusing on their robustness to outliers. The experiment varies the dimensionality (number of features) of the data, while keeping other factors (sample size, outlier contamination levels, etc) constant. The excess risk (the difference between the achieved risk and the minimum achievable risk) is plotted against the dimension. Error bars show standard deviations across multiple trials, demonstrating the stability of each method. The results show UOT-DRO consistently demonstrates lower excess risk across various dimensions, indicating improved robustness to outliers compared to the other methods.
read the caption
Figure 4: Excess risk and accuracy of standard DRO, OR-WDRO, and UOT-DRO with varied dimensions for linear classification. The error bar denotes ± standard deviation.

🔼 This figure compares the performance of three different distributionally robust optimization (DRO) methods for linear classification tasks across different feature dimensions (d). The x-axis represents the feature dimension, while the y-axis shows both the excess risk (how much worse the model’s performance is compared to the best achievable performance) and the accuracy (percentage of correctly classified samples). The figure shows that the proposed UOT-DRO method consistently outperforms standard DRO and OR-WDRO across all feature dimensions, indicating better robustness and generalization.
read the caption
Figure 4: Excess risk and accuracy of standard DRO, OR-WDRO, and UOT-DRO with varied dimensions for linear classification. The error bar denotes ± standard deviation.
More on tables

🔼 This table presents the results of a linear classification experiment, comparing the performance of three different methods (Standard DRO, OR-WDRO, and UOT-DRO) under varying levels of data contamination (represented by the ‘Contamin. C’ column). For each contamination level, the table shows the excess risk and accuracy achieved by each method. Excess risk measures the difference between the achieved loss and the minimum possible loss, while accuracy represents the percentage of correctly classified data points. The results illustrate the robustness of the proposed UOT-DRO method to outliers compared to the other two methods.
read the caption
Table 2: Excess risk with various contamination for linear classification.
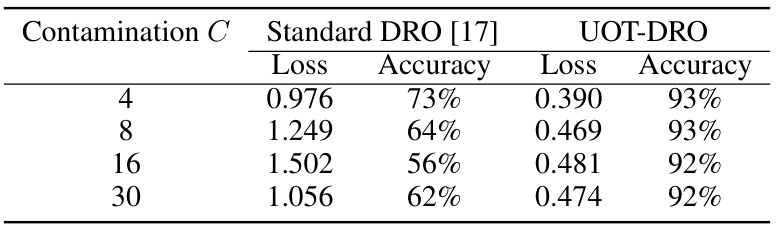
🔼 This table presents a comparison of excess risk and accuracy for three different methods (Standard DRO, OR-WDRO, and UOT-DRO) in a linear classification problem with varying levels of data contamination (C). It demonstrates the robustness of the UOT-DRO method against outliers, as its performance remains consistent across different contamination levels, unlike the other two methods.
read the caption
Table 2: Excess risk with various contamination for linear classification.

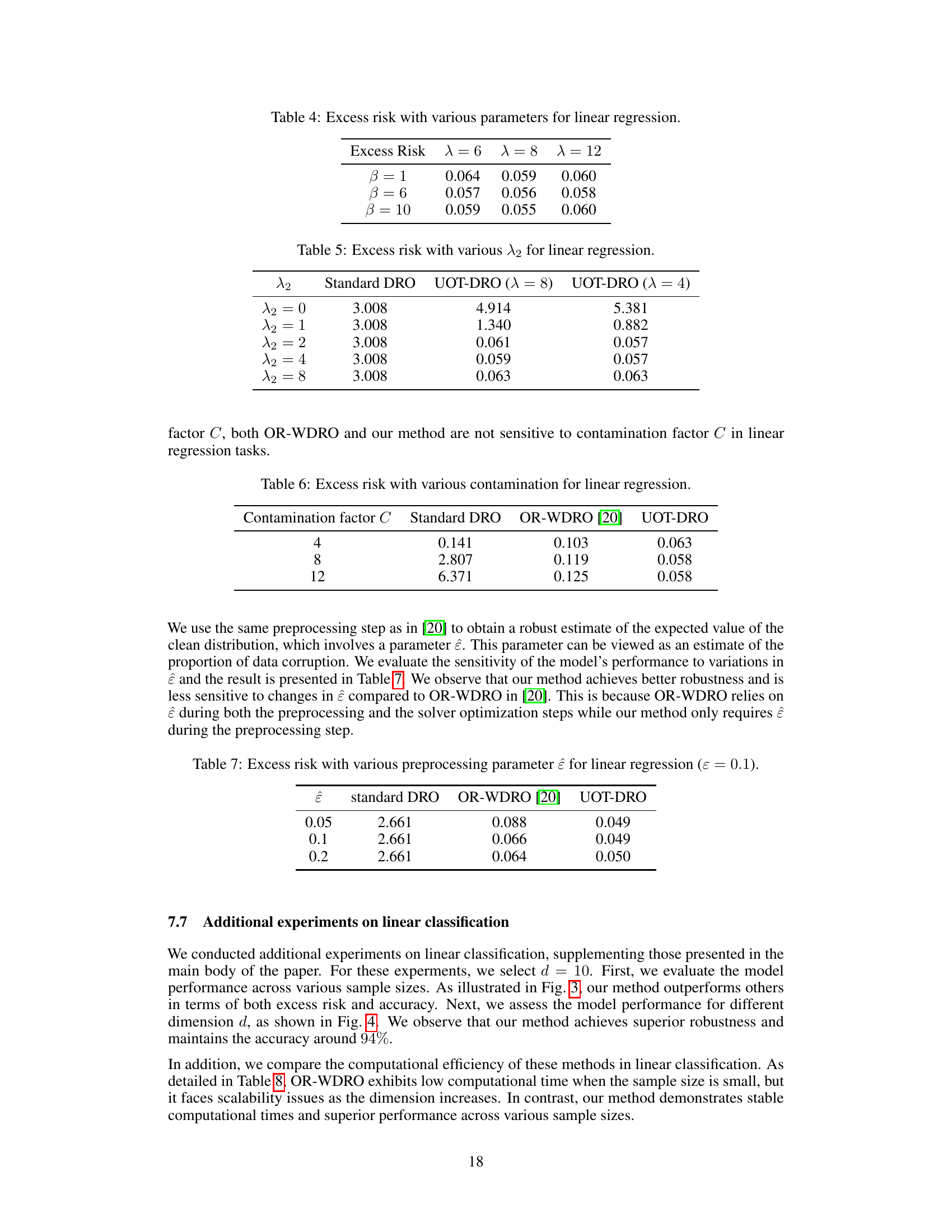
🔼 This table shows the excess risk for different combinations of lambda (λ) and beta (β) parameters in the linear regression experiment. The results demonstrate that the model’s performance shows minimal sensitivity to variations in these parameters across a range of values.
read the caption
Table 4: Excess risk with various parameters for linear regression.
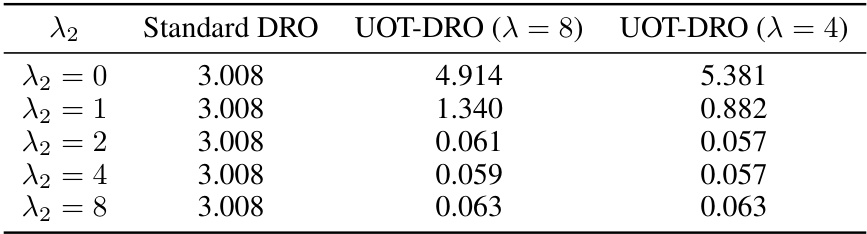
🔼 This table presents the excess risk achieved by standard DRO and UOT-DRO methods under different values of the parameter λ2. The parameter λ2 controls the weight given to prior knowledge in identifying outliers. The table shows that the UOT-DRO method is significantly more robust to outliers, achieving a much lower excess risk than the standard DRO, particularly when λ2 is greater than 1.
read the caption
Table 5: Excess risk with various λ2 for linear regression.

🔼 This table compares the excess risk of three different methods (Standard DRO, OR-WDRO, and UOT-DRO) for linear regression under different levels of data contamination. The contamination factor (C) represents the degree of data corruption. The excess risk is a measure of the model’s performance relative to the optimal performance. Lower values of excess risk indicate better performance.
read the caption
Table 6: Excess risk with various contamination for linear regression.

🔼 This table compares the excess risk of standard DRO, OR-WDRO [20], and UOT-DRO for linear regression with different values of the preprocessing parameter ĉ (epsilon). The parameter ĉ represents the estimated proportion of data corruption. The table shows how sensitive each method is to variations in ĉ.
read the caption
Table 7: Excess risk with various preprocessing parameter ĉ for linear regression (ε = 0.1).
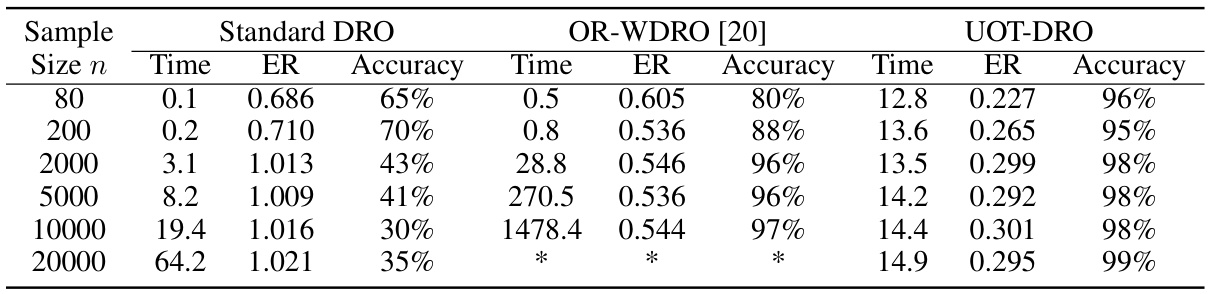
🔼 This table compares the computational time and excess risk (difference between obtained loss and minimum achievable loss) of three different methods for linear regression: Standard DRO, OR-WDRO [20], and the proposed UOT-DRO. The excess risk and computational time are shown for different sample sizes (n). The ‘*’ symbol indicates that the running time exceeded 12000 seconds for the OR-WDRO method, highlighting its computational inefficiency compared to the UOT-DRO method, particularly for larger datasets.
read the caption
Table 1: Comparison of running time and excess risk of different methods for linear regression. The symbol '*' indicates that running time is over 12000 seconds.

🔼 This table compares the excess risk and accuracy of three different methods (Standard DRO, OR-WDRO, and UOT-DRO) for linear classification with varying levels of data corruption (represented by the parameter ĉ). The results show the robustness of UOT-DRO against changes in the corruption level, maintaining high accuracy.
read the caption
Table 9: Excess risk with various ĉ for linear classification.

🔼 This table shows the accuracy of the UOT-DRO model for different values of parameters β (beta) and λ (lambda) in a linear classification task where the contamination factor C is 10. The accuracy is compared to standard DRO and OR-WDRO methods to highlight the robustness of the UOT-DRO approach and its insensitivity to parameter tuning. The wide range of accuracies for different parameter choices indicates the method’s stability.
read the caption
Table 10: Accuracy of various parameters for linear classification when C = 10. Standard DRO: 66%; OR-WDRO: 79%.

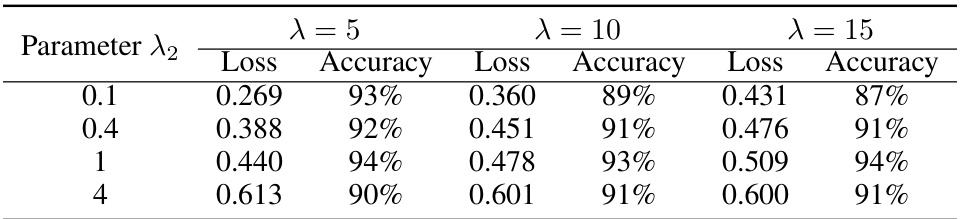
🔼 This table presents the loss and accuracy of the logistic regression model using the proposed UOT-DRO method with varying values of the parameter β. The results are shown for three different values of the parameter λ (5, 10, and 15), demonstrating the impact of β on the model’s performance across different levels of regularization.
read the caption
Table 11: Loss and accuracy of various β for logistic regression.
🔼 This table presents the excess risk of standard DRO and UOT-DRO with various λ2 for linear regression. λ2 is a parameter that represents the credibility level assigned to the function h, which is designed based on prior knowledge about the data distribution. A larger value of λ2 indicates higher confidence in h, meaning that h(ξ) is more likely to be larger at outlier points. The results show the impact of λ2 on model performance under different values of λ, illustrating the trade-off between robustness and performance based on prior knowledge.
read the caption
Table 5: Excess risk with various λ2 for linear regression.
Full paper#