↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
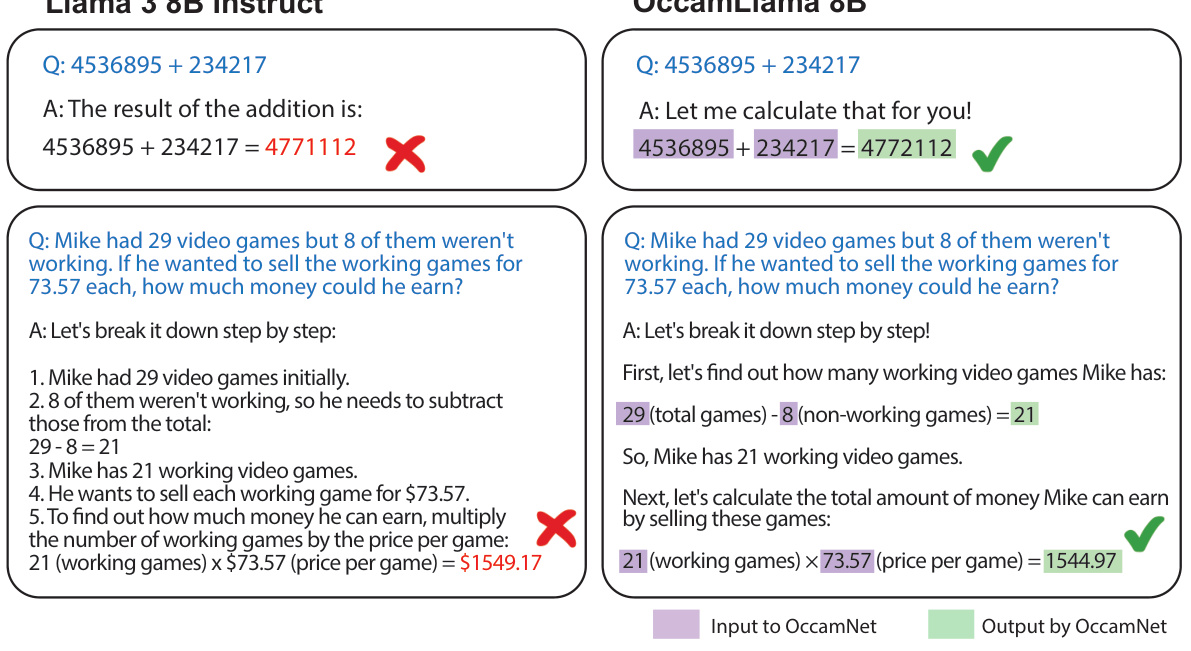
Large Language Models (LLMs) struggle with accurate arithmetic, often relying on slow and insecure code generation. This paper introduces OccamLLM, a novel framework addressing this issue. Current methods compromise speed and security, and fine-tuning risks catastrophic forgetting. LLMs’ inability to perform basic mathematical operations also hinders their application in diverse fields.
OccamLLM achieves 100% accuracy on single-step arithmetic operations (+,-,×,÷,sin,cos,log,exp,√) using a symbolic architecture controlled by the LLM’s hidden states. This single-step process is faster, more secure, and more interpretable than generating code. Benchmarking shows OccamLLM outperforms GPT-4 (with and without code interpreter) on various mathematical problem-solving tasks, demonstrating its superior performance. The research highlights a new paradigm for LLM arithmetic and opens avenues for enhancing various AI systems.
Key Takeaways#
Why does it matter?#
This paper is crucial because it introduces a novel framework for accurate and efficient arithmetic within LLMs, a significant limitation in current models. This addresses a critical bottleneck in various applications, paving the way for faster, more secure, and interpretable AI systems. The framework’s simplicity and effectiveness open exciting avenues for future research into improving LLM capabilities and creating more sophisticated AI tools. It significantly advances interpretable LLM arithmetic, impacting areas like multi-agent systems and LLM-powered scientific discovery.
Visual Insights#

This figure illustrates the architecture of the OccamLLM system. The system combines a large language model (LLM) with a symbolic model called OccamNet to perform arithmetic operations. For each token in the input sequence, the LLM’s hidden states are used by a decoder to assign weights to OccamNet. OccamNet then uses these weights and the relevant numbers from the input text to perform the calculation. Finally, a switch decides whether to output the LLM’s prediction or OccamNet’s result.
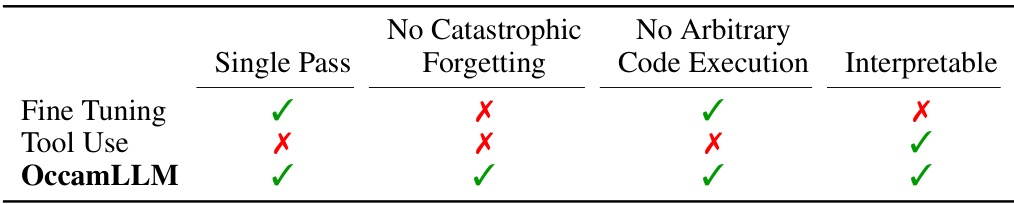
This table compares different methods for improving the arithmetic capabilities of pretrained LLMs along four key aspects: single-pass arithmetic, risk of catastrophic forgetting due to finetuning, need for arbitrary code execution, and interpretability of the process. It highlights that OccamLLM uniquely excels in all four aspects.
In-depth insights#
OccamLLM’s Speed#
OccamLLM’s speed advantage stems from its unique single-step arithmetic operation. Unlike traditional LLMs that generate code for calculations, significantly increasing latency, OccamLLM leverages a symbolic architecture (OccamNet) controlled by the LLM’s hidden states. This allows for direct, immediate arithmetic within the autoregressive generation process. The result is a substantial speedup compared to methods relying on code generation or external tool use, as demonstrated by OccamLLM’s performance exceeding GPT-4, even GPT-4 with Code Interpreter, on several benchmarks, often using orders of magnitude fewer tokens. This enhanced efficiency is crucial for real-time applications and multi-agent systems where rapid computation is essential. However, the speed benefit might vary depending on the specific computational graph generated by OccamNet, which inherently introduces some variability. While generally very fast, specific complex arithmetic expressions could potentially demand more computational time. OccamLLM’s efficiency hinges on the efficient design of the OccamNet and the decoder’s ability to quickly select and apply appropriate arithmetic operations.
Single-Step Arith#
The concept of “Single-Step Arith” in the context of large language models (LLMs) signifies a significant advancement in enabling LLMs to perform arithmetic operations efficiently and accurately. Traditional methods often involve multi-step processes, like generating code to perform calculations, which are slow and can introduce security vulnerabilities. Single-step arithmetic directly addresses these issues by integrating arithmetic computation within the LLM’s autoregressive process, allowing for a single step calculation. This approach drastically improves speed and security while maintaining the LLM’s core capabilities, making the process faster and less vulnerable to errors. The core innovation likely involves a novel architecture or technique that allows the LLM to directly manipulate numerical representations within its hidden states, thereby facilitating immediate arithmetic computation without the need for intermediate code generation. The success of single-step arithmetic hinges on the model’s capability to accurately interpret and integrate numerical data within its internal representation, leading to precise and fast arithmetic abilities. Interpretability is another important aspect, as the method likely provides insights into the LLM’s internal arithmetic processing, enhancing transparency and facilitating further optimization and debugging. Overall, “Single-Step Arith” presents a significant step towards creating more efficient, secure, and interpretable LLMs with enhanced arithmetic reasoning capabilities.
Symbolic Control#
The concept of ‘Symbolic Control’ in the context of large language models (LLMs) centers on using symbolic representations and architectures to manage and direct the LLM’s internal mechanisms. This contrasts with traditional approaches that rely solely on statistical methods. Symbolic control offers several key advantages: enhanced interpretability, facilitating the understanding of LLM decision-making; increased precision and reliability in tasks requiring exact calculations or logical reasoning; and enhanced security by limiting reliance on potentially unsafe code generation. A crucial aspect of symbolic control involves the design of an interface between the symbolic system and the LLM’s internal state, allowing the symbolic system to influence the LLM’s output. The effectiveness of symbolic control hinges on the seamless integration of symbolic and neural computation, demanding further exploration into methods for efficiently bridging the gap between the discrete nature of symbolic systems and the continuous, probabilistic representation within neural networks. A key challenge lies in designing the symbolic control mechanisms to avoid catastrophic forgetting, or the LLM losing its previously learned abilities through the introduction of external knowledge or training. The successful implementation of symbolic control would lead to more robust, interpretable, and trustworthy LLMs with advanced reasoning capabilities.
OccamNet’s Role#
OccamNet serves as a neurosymbolic arithmetic engine within the OccamLLM framework. Instead of relying on external tools or code generation, OccamNet uses the LLM’s hidden states to directly control its operations. This approach is computationally efficient and interpretable, offering improved speed and security. OccamNet’s symbolic architecture allows for precise arithmetic calculations in a single autoregressive step, enhancing LLM capabilities without the risks associated with finetuning or external code execution. The model’s interpretability is a significant advantage, facilitating a deeper understanding of the LLM’s arithmetic reasoning. The choice of OccamNet over other symbolic models is motivated by its interpretability and scalability, making it well-suited for integration with LLMs.
Future Research#
Future research directions stemming from this OccamLLM work are rich and impactful. Extending OccamNet’s capabilities beyond single-step arithmetic to handle more complex mathematical expressions and multi-step reasoning problems is crucial. This involves exploring deeper and more sophisticated symbolic architectures, potentially incorporating other tools. Improving the OccamLLM switch’s robustness and generalization across diverse prompts and linguistic styles is another key area. Addressing catastrophic forgetting in other tool-using LLM approaches, by exploring alternative training methodologies, remains a relevant concern. Further research into safe and effective techniques for integrating OccamLLM with larger LLMs is essential for creating even more powerful systems. Finally, investigating the potential for OccamLLM to enhance other aspects of LLM functionality, such as code generation and reasoning, represents a significant opportunity for broader impact.
More visual insights#
More on figures
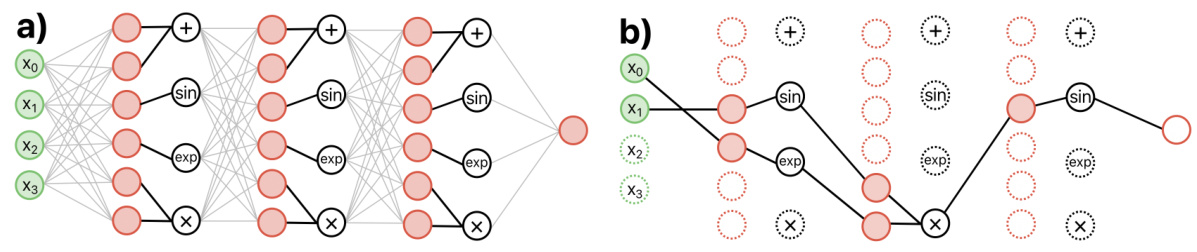
This figure shows a schematic of the OccamLLM system architecture. It illustrates how the hidden states of a language model are used to control a symbolic model called OccamNet for arithmetic computations. The system takes the language model’s hidden states for a given token as input. These states are fed into a decoder block, which assigns weights to OccamNet based on the task at hand (e.g., addition, subtraction, etc.). OccamNet receives numerical inputs from the text and, based on the weights assigned by the decoder, performs the computation. Finally, a decision is made to use either the output from OccamNet or the output from the language model for the next autoregressive step in text generation.

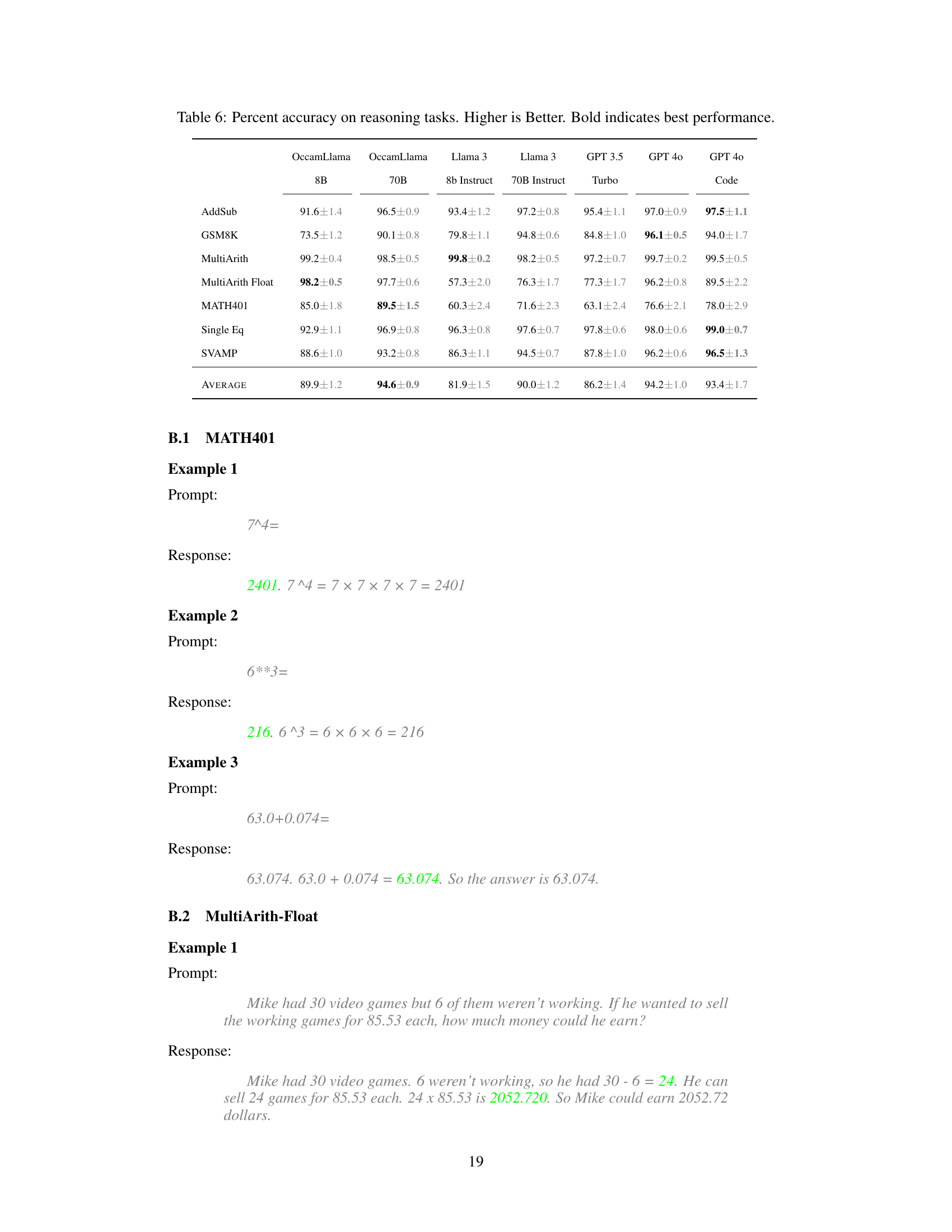
This figure compares the accuracy of OccamLlama models (8B and 70B parameters) against several baseline LLMs (Llama 2 7B, Llama 3 8B and 70B, GPT 3.5 Turbo, GPT 4, and GPT 4 with code interpreter) on six mathematical problem-solving benchmarks (AddSub, GSM8K, MultiArith, MultiArith Float, MATH401, Single Eq, and SVAMP). The results demonstrate that OccamLlama, especially the larger 70B parameter model, significantly outperforms the baselines, particularly on tasks involving more challenging arithmetic.
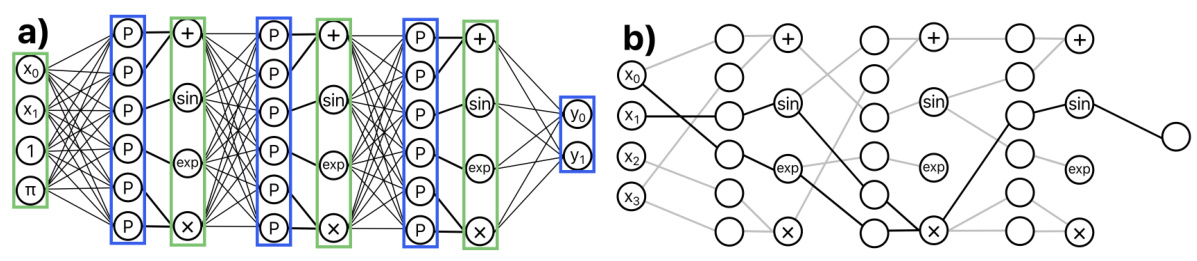
This figure illustrates the architecture of the OccamLLM system. It shows how the hidden states of a language model are used to control a symbolic model (OccamNet) for arithmetic operations. The system performs an autoregressive step, feeding the hidden states to a decoder that determines OccamNet’s weights for the operation. The numbers from the input text are then fed to OccamNet, which computes the result. Finally, a decoder decides whether to use the LLM’s output or OccamNet’s result for the next token.

This figure compares the performance of OccamLlama (8B and 70B parameter versions), Llama 2 7B Chat, Llama 3 (8B and 70B parameter versions), GPT 3.5 Turbo, GPT 4, and GPT 4 with code interpreter on six mathematical problem-solving benchmarks. It demonstrates OccamLlama’s superior performance, particularly on tasks involving complex arithmetic.
This figure illustrates the architecture of the OccamLLM system. It shows how the hidden states of a language model (LLM) are used to control a symbolic model called OccamNet. The LLM’s hidden states are input to a decoder which assigns weights to OccamNet, determining which arithmetic operation OccamNet performs. Numbers from the text are passed to OccamNet, which computes the result. Finally, a decision is made whether to use the output from OccamNet or the LLM, selecting the most appropriate output for that step in text generation.

This figure illustrates the architecture of the OccamLLM system. The system uses a language model (LLM) in conjunction with a symbolic model (OccamNet) to perform arithmetic calculations within a single autoregressive step. The LLM’s hidden states influence the weights assigned to OccamNet, which then processes numerical inputs from the text. A decoder decides whether to use the LLM’s output or OccamNet’s output for the next token generation.
More on tables
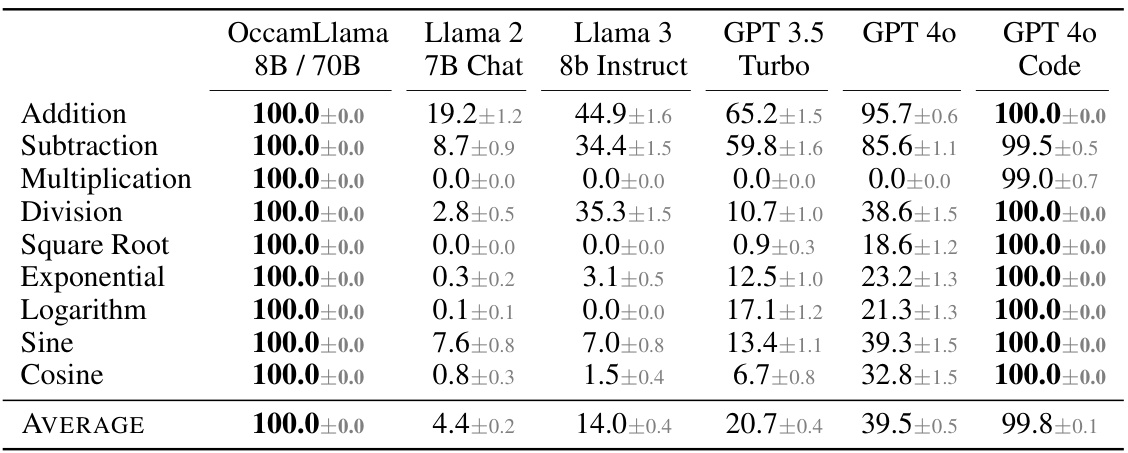
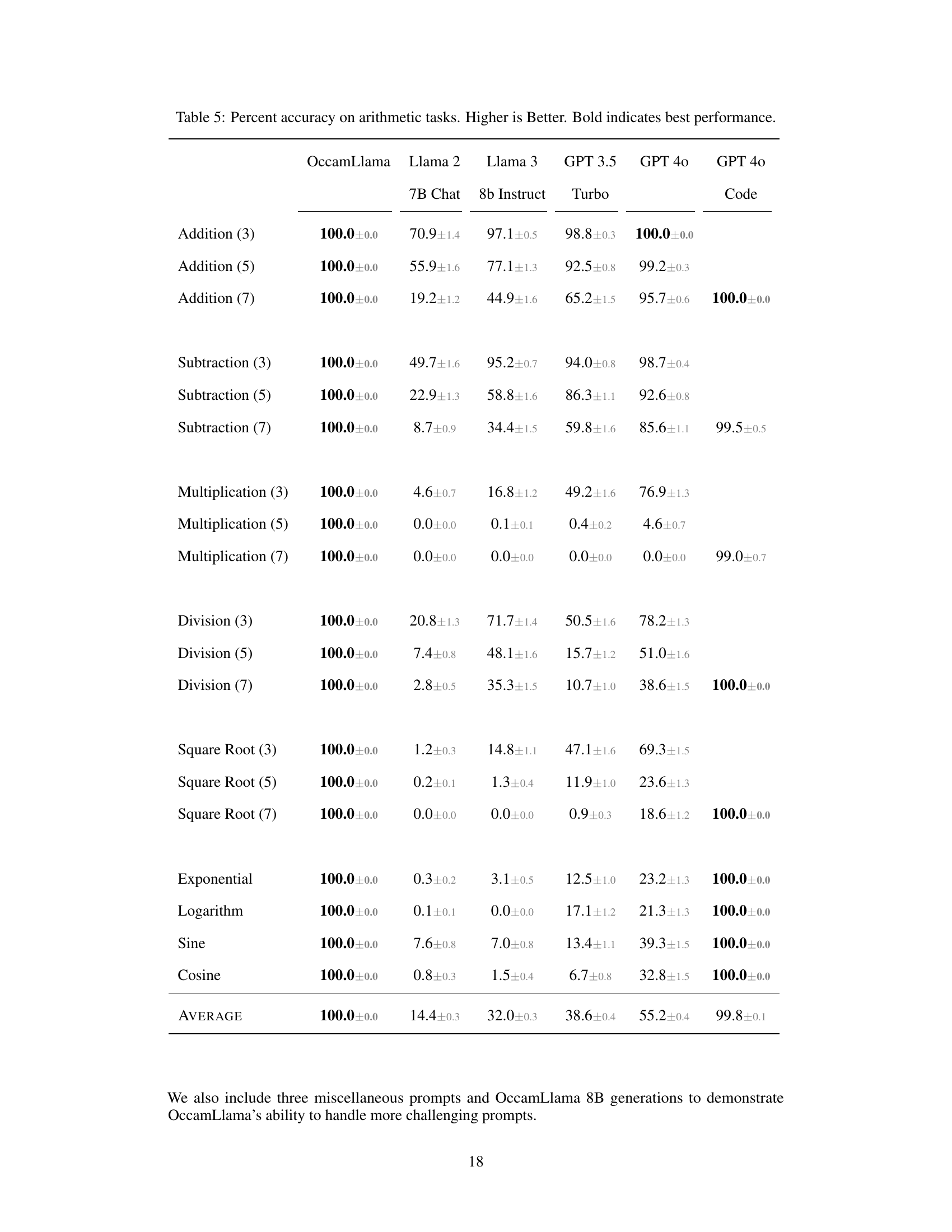
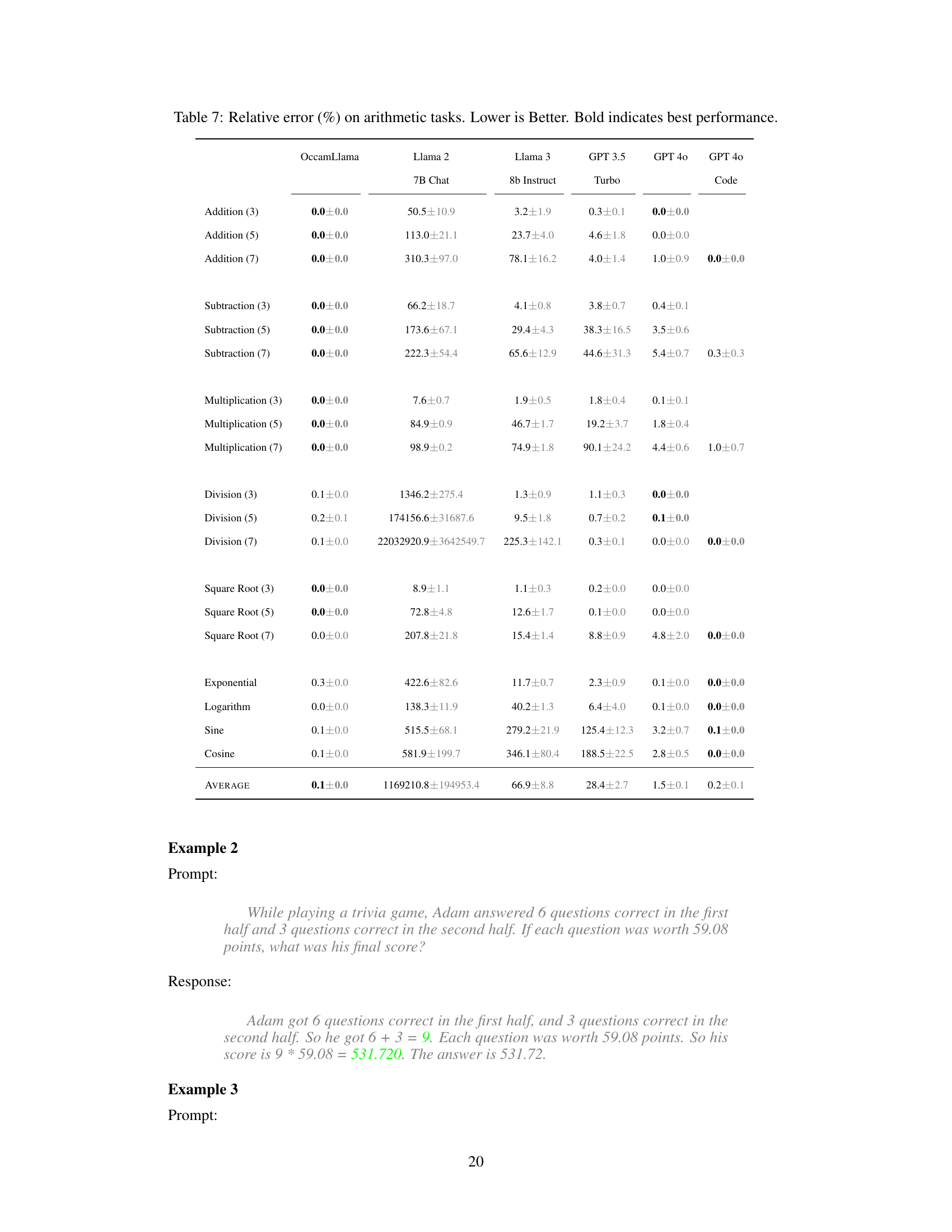
This table presents the accuracy of different language models on various arithmetic tasks. The accuracy is shown as a percentage, with higher percentages indicating better performance. The models compared are OccamLlama 8B, OccamLlama 70B, Llama 2 7B Chat, Llama 3 8b Instruct, GPT 3.5 Turbo, and GPT 40 (with and without code interpreter). The arithmetic tasks include addition, subtraction, multiplication, division, square root, exponential, logarithm, sine, and cosine. OccamLlama consistently achieves 100% accuracy, significantly outperforming other models, especially on more complex operations.
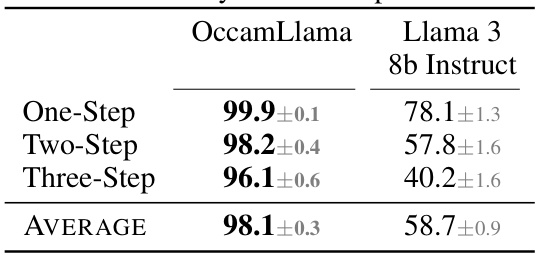
This table compares the accuracy of OccamLlama and Llama 3 8B Instruct on multi-step arithmetic tasks (one-step, two-step, and three-step). It demonstrates OccamLlama’s ability to handle increasingly complex arithmetic operations with high accuracy, even outperforming Llama 3 8B significantly, especially as the number of steps increases.

This table compares the accuracy of various language models on a series of arithmetic tasks, including addition, subtraction, multiplication, division, square root, exponential, logarithm, sine, and cosine. The accuracy is presented as a percentage, with standard error included. OccamLlama consistently achieves 100% accuracy, significantly outperforming other models, especially on more complex operations.

This table presents the accuracy of different language models on various arithmetic tasks, including addition, subtraction, multiplication, division, square root, exponential, logarithm, sine, and cosine. The accuracy is measured as a percentage and presented with error bars. OccamLlama consistently achieves 100% accuracy, significantly outperforming other models, particularly on more complex operations.

This table presents the accuracy of different language models on various arithmetic tasks, including addition, subtraction, multiplication, division, square root, exponential, logarithm, sine, and cosine. The accuracy is measured as a percentage, with higher percentages indicating better performance. The results for OccamLlama represent the average performance of both the 8B and 70B versions of the model. The table highlights the superior accuracy of OccamLlama compared to other models, especially on more complex arithmetic operations.
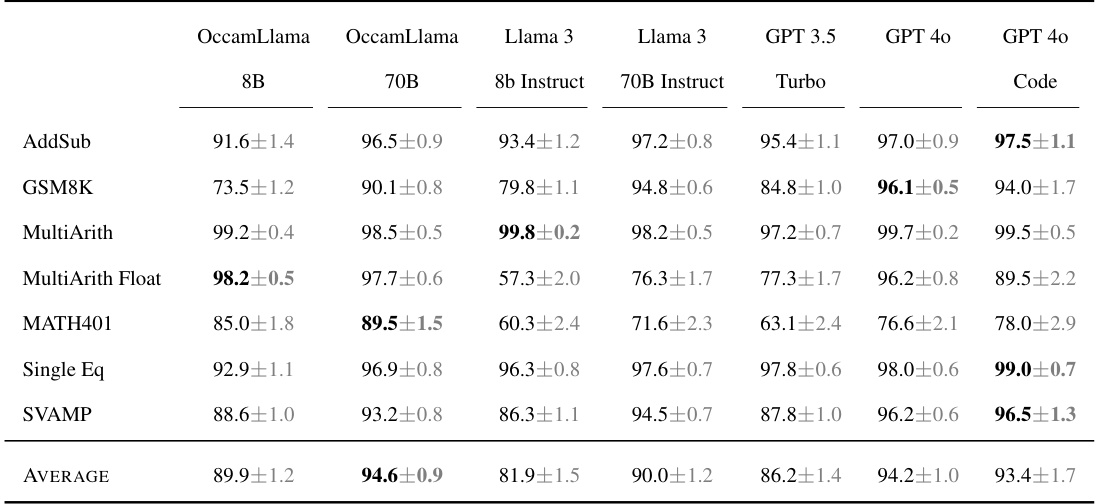
This table presents the accuracy of various LLMs on mathematical reasoning tasks. The LLMs are compared across several benchmarks (AddSub, GSM8K, MultiArith, MultiArith Float, MATH401, Single Eq, SVAMP). The accuracy is expressed as a percentage with error bars. OccamLlama models (8B and 70B) show superior performance compared to baselines like Llama 3 and GPT models, especially on tasks with challenging arithmetic.
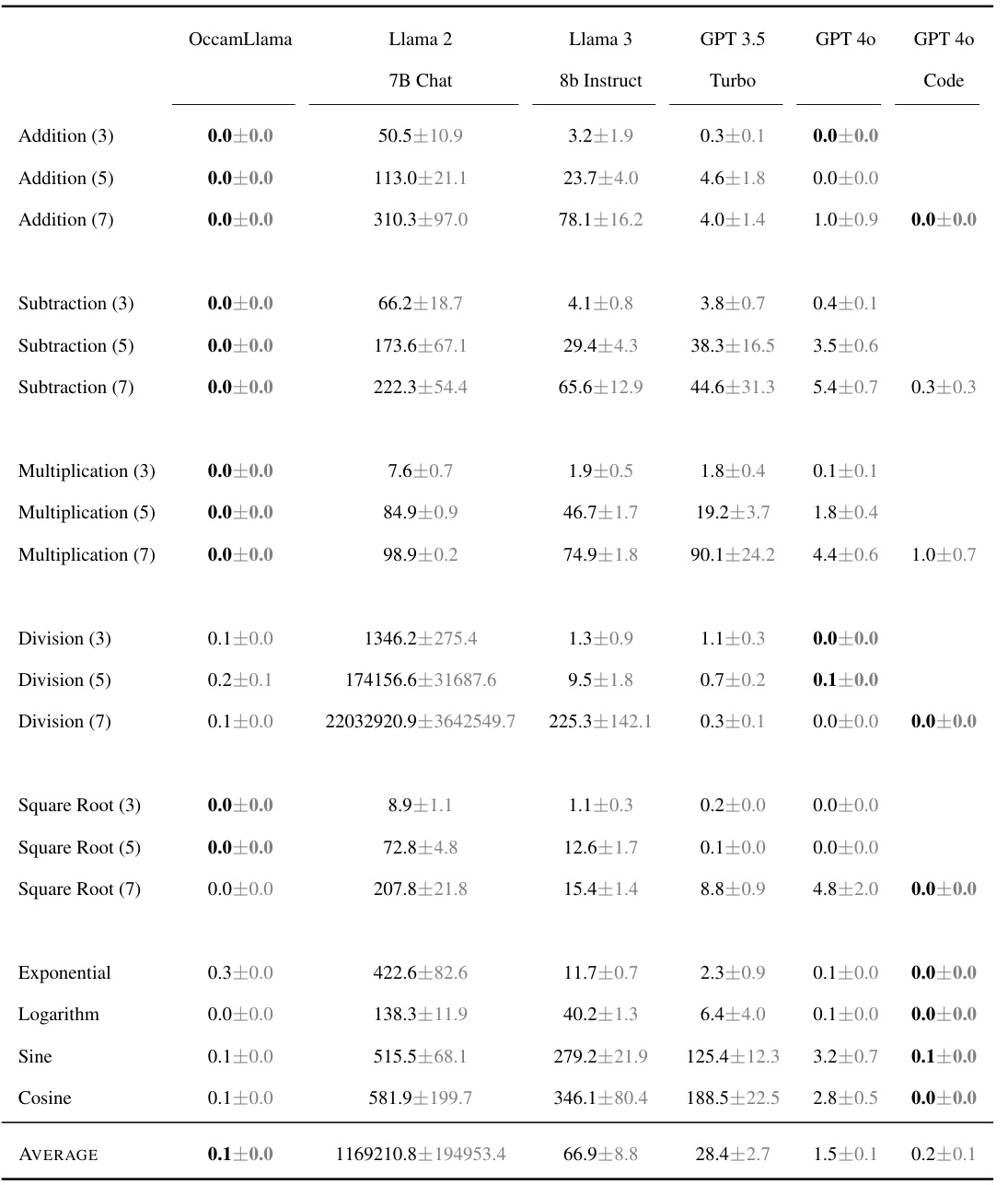
This table presents the accuracy of different language models on various arithmetic tasks (addition, subtraction, multiplication, division, square root, exponential, logarithm, sine, cosine). The accuracy is expressed as a percentage, with the OccamLlama models (OccamLlama 8B and 70B) showing 100% accuracy on all tasks. Other models, such as Llama 2, Llama 3, GPT 3.5 Turbo, and GPT 40 (with and without code interpreter), show significantly lower accuracy, highlighting the superior performance of OccamLlama on arithmetic tasks.
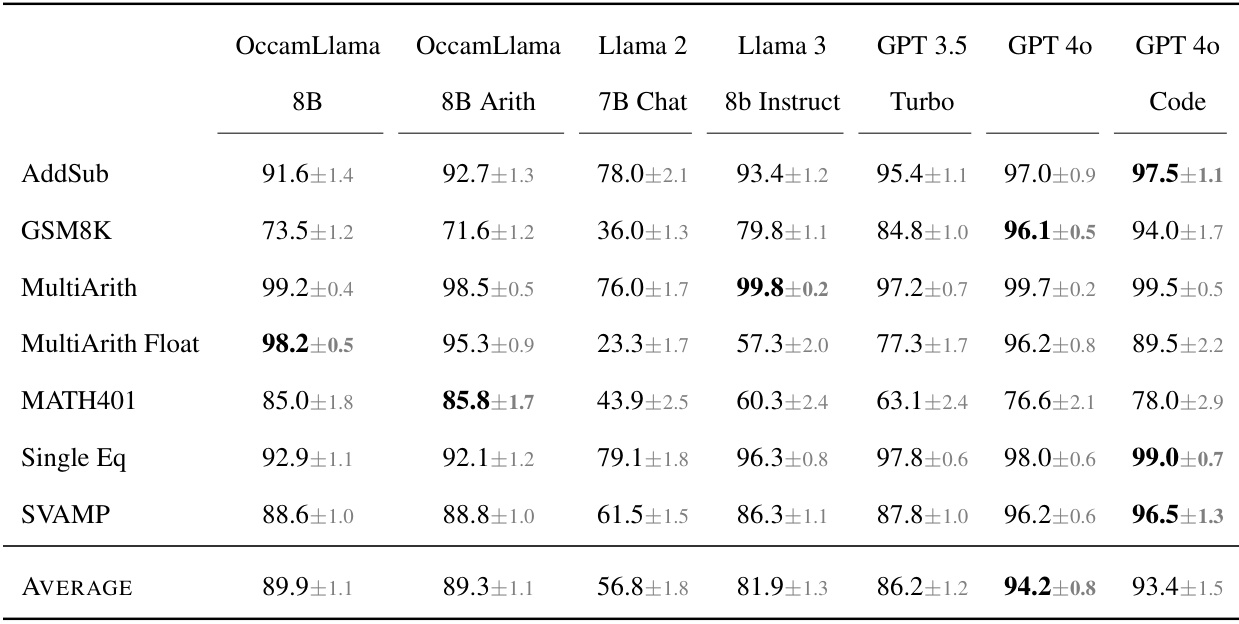
This table presents the accuracy of various language models on mathematical reasoning tasks. The models are compared across six different benchmarks (AddSub, GSM8K, MultiArith, MultiArith Float, MATH401, Single Eq, SVAMP), each designed to test different aspects of mathematical reasoning ability. The table shows the percentage accuracy for each model on each benchmark, highlighting the best-performing model for each benchmark in bold. The results show that OccamLlama consistently outperforms other models, especially on more challenging tasks.
Full paper#