↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Current methods for enhancing LLMs’ mathematical reasoning abilities heavily rely on high-quality, process-supervised data, which is expensive and time-consuming to obtain. This often involves human annotation or assistance from powerful models like GPT-4. This creates a bottleneck in advancing research in this area.
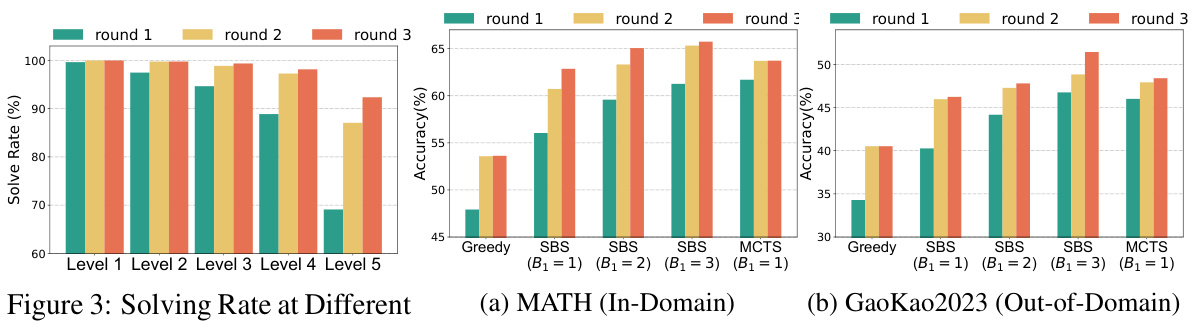
The proposed AlphaMath framework bypasses this limitation. It leverages Monte Carlo Tree Search (MCTS) and a value model to enable an LLM to generate its own process supervision and step-level evaluation signals. An efficient inference strategy, step-level beam search, further enhances performance. Experiments show that AlphaMath performs competitively with state-of-the-art methods even without external high-quality annotations.
Key Takeaways#
Why does it matter?#
This paper is important because it presents AlphaMath, a novel framework that significantly advances mathematical reasoning in LLMs without relying on expensive and time-consuming human or GPT-4 annotations. This addresses a critical limitation of existing methods and opens up new avenues for research in LLM development and applications.
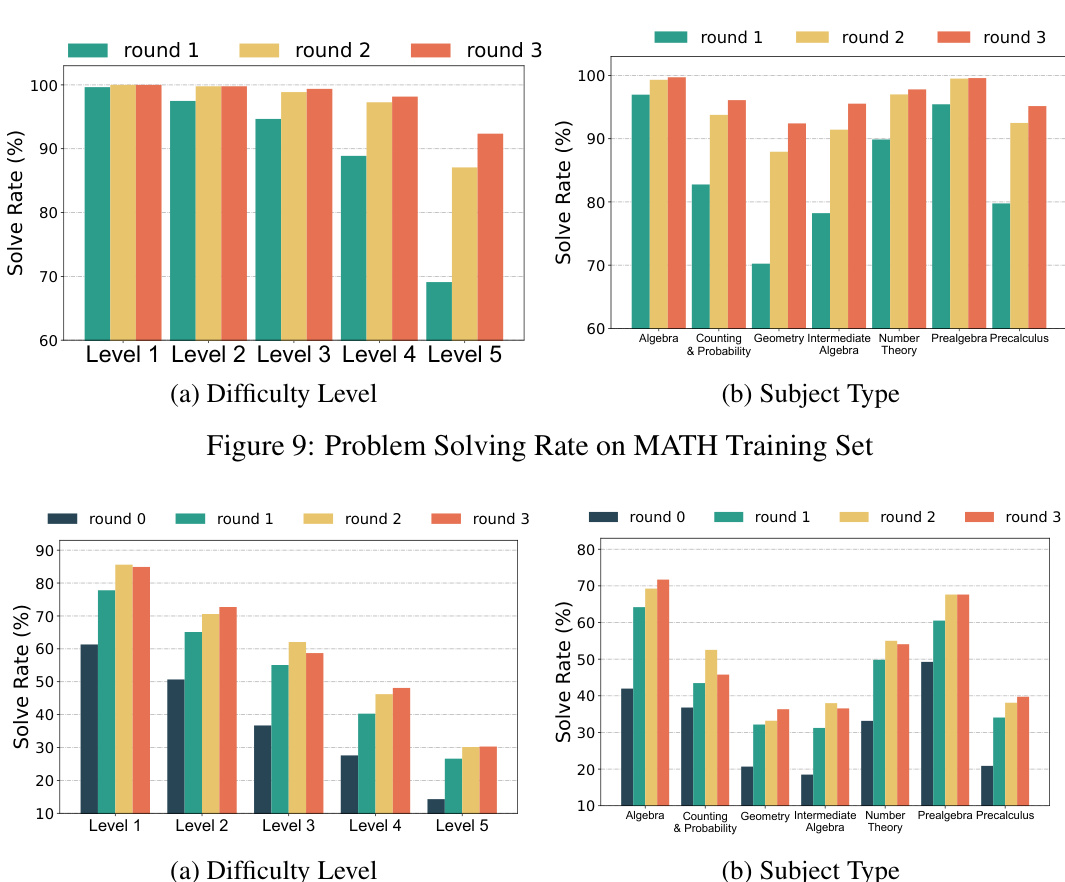
Visual Insights#

This figure illustrates the iterative training process of AlphaMath. It starts with a mathematical dataset containing questions and answers. The AlphaMath framework then uses Monte Carlo Tree Search (MCTS) with a policy model (LLM) and a value model to generate solution paths. These paths, including both correct and incorrect ones, along with their associated state values, are used to iteratively train and improve the policy and value models. This iterative process allows AlphaMath to learn and enhance its mathematical reasoning capabilities without explicit process supervision.
This table presents the main results of the AlphaMath model and compares it to various other models on both in-domain and out-of-domain datasets. It shows the performance of different models across various metrics, including the use of different tools, the amount of seed data used, the annotation sources used for the seed data, and the overall performance achieved. The table highlights the performance of AlphaMath, both with and without the step-level beam search (SBS) and Monte Carlo Tree Search (MCTS) methods, demonstrating its effectiveness.
In-depth insights#
AlphaMath: Zero-Shot#
The hypothetical concept of “AlphaMath: Zero-Shot” suggests a novel approach to mathematical reasoning in large language models (LLMs). A zero-shot approach implies that the model, after initial training, can tackle mathematical problems without explicit examples or fine-tuning on specific tasks. This eliminates the need for costly and time-consuming process annotation, a significant limitation of existing LLM-based methods. AlphaMath likely leverages a strong pre-trained LLM and incorporates techniques like Monte Carlo Tree Search (MCTS) or beam search for efficient exploration of solution paths. A value model would be crucial, dynamically evaluating the quality of intermediate steps during the search, allowing for intelligent navigation towards correct solutions and bypassing reliance on solely prior probabilities. The core innovation is the model’s ability to learn and improve its mathematical reasoning through self-supervised learning from its own generated solutions, iteratively enhancing its knowledge base without external expert guidance. This self-evolution is key to AlphaMath’s zero-shot capability and potentially outperforms state-of-the-art methods that rely on heavily annotated datasets.
MCTS-based Training#
The core idea revolves around using Monte Carlo Tree Search (MCTS) to generate high-quality, process-supervised training data for LLMs without human annotation. MCTS guides the LLM to explore different solution paths, creating a dataset of both correct and incorrect reasoning steps with associated state values. This process is iterative, allowing the LLM and a value model to improve concurrently. The value model learns to assess the quality of intermediate reasoning steps, helping the LLM navigate more effective reasoning paths during inference. This eliminates the costly and time-consuming process of human or GPT-4 annotation, while simultaneously enhancing the LLM’s reasoning abilities and its understanding of mathematical problem-solving strategies.
Step-Level Beam Search#
The proposed step-level beam search is a significant optimization to enhance the efficiency of the Monte Carlo Tree Search (MCTS) algorithm in mathematical problem-solving. Instead of performing multiple simulations from each state in the MCTS, as traditionally done, this method leverages a lightweight value model to directly assess the quality of intermediate steps, thereby accelerating inference. This strategy closely mimics human reasoning, allowing for quick evaluation and selection of promising solution paths during the search process, without the need for time-consuming rollouts for reward estimations. The integration of the value model allows the LLM to navigate more effective solution paths, as opposed to solely relying on prior probabilities. The step-level approach, in conjunction with beam search, makes AlphaMath efficient and practical for real-world applications, making it scalable and deployable in production environments where computational resources are limited. The performance gains highlight the potential of combining LLMs with a carefully designed search strategy to achieve results competitive with or even surpassing state-of-the-art methods that depend on expensive and labor-intensive human annotations or GPT-4 assistance.
Limitations and Future#
The study’s limitations primarily revolve around the reliance on readily available question-answer pairs for training, limiting the exploration of a truly unsupervised approach. While this simplifies data acquisition compared to process-supervised methods, it restricts the framework’s ability to learn completely from scratch. Future work should focus on developing a truly unsupervised reward model, eliminating the need for ground-truth answers. This would entail creating a system capable of autonomously assessing the quality of reasoning paths. Further investigation into the applicability of the AlphaMath framework to other domains beyond mathematical reasoning is also warranted, which could unlock its potential for various complex reasoning tasks. Investigating the effects of different model architectures and the impact of varying hyperparameters also present valuable avenues for future improvement. Finally, a thorough analysis of the computational efficiency and scalability of the methods for real-world applications is needed.
Value Model’s Role#
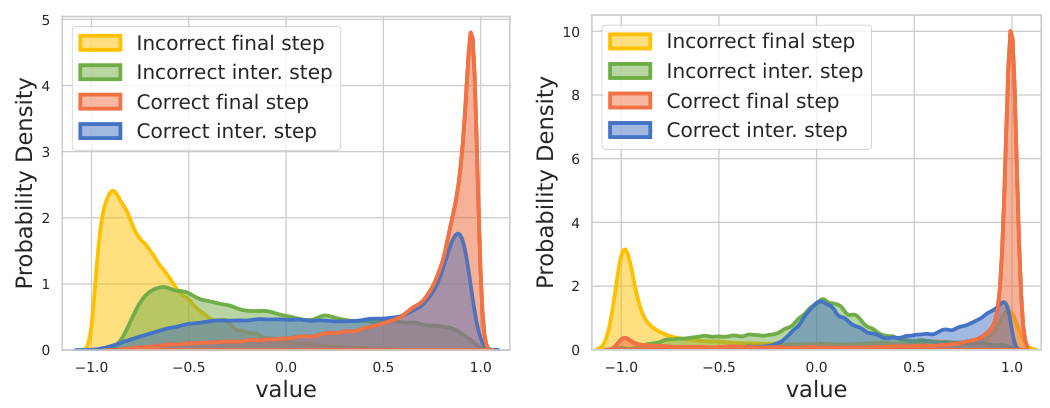
The paper’s value model plays a crucial role in enhancing the LLM’s mathematical reasoning capabilities. It assesses the quality of intermediate reasoning steps, providing valuable feedback during the Monte Carlo Tree Search (MCTS) process. Unlike methods relying solely on final answer accuracy, this step-level evaluation guides the LLM towards more effective reasoning paths. By integrating with the LLM, the value model avoids time-consuming rollouts, improving efficiency. The value model’s estimations are used in the step-level beam search, further enhancing the LLM’s ability to navigate complex problems effectively. This synergy between the policy (LLM) and value models mimics human problem-solving, where intermediate steps are evaluated and potentially revised. The experimental results demonstrate the value model’s effectiveness in achieving comparable or superior results to prior state-of-the-art methods, even without the need for expensive human-annotated process supervision. Its impact is especially evident in more challenging datasets, highlighting its significant contribution to AlphaMath’s success.
More visual insights#
More on figures

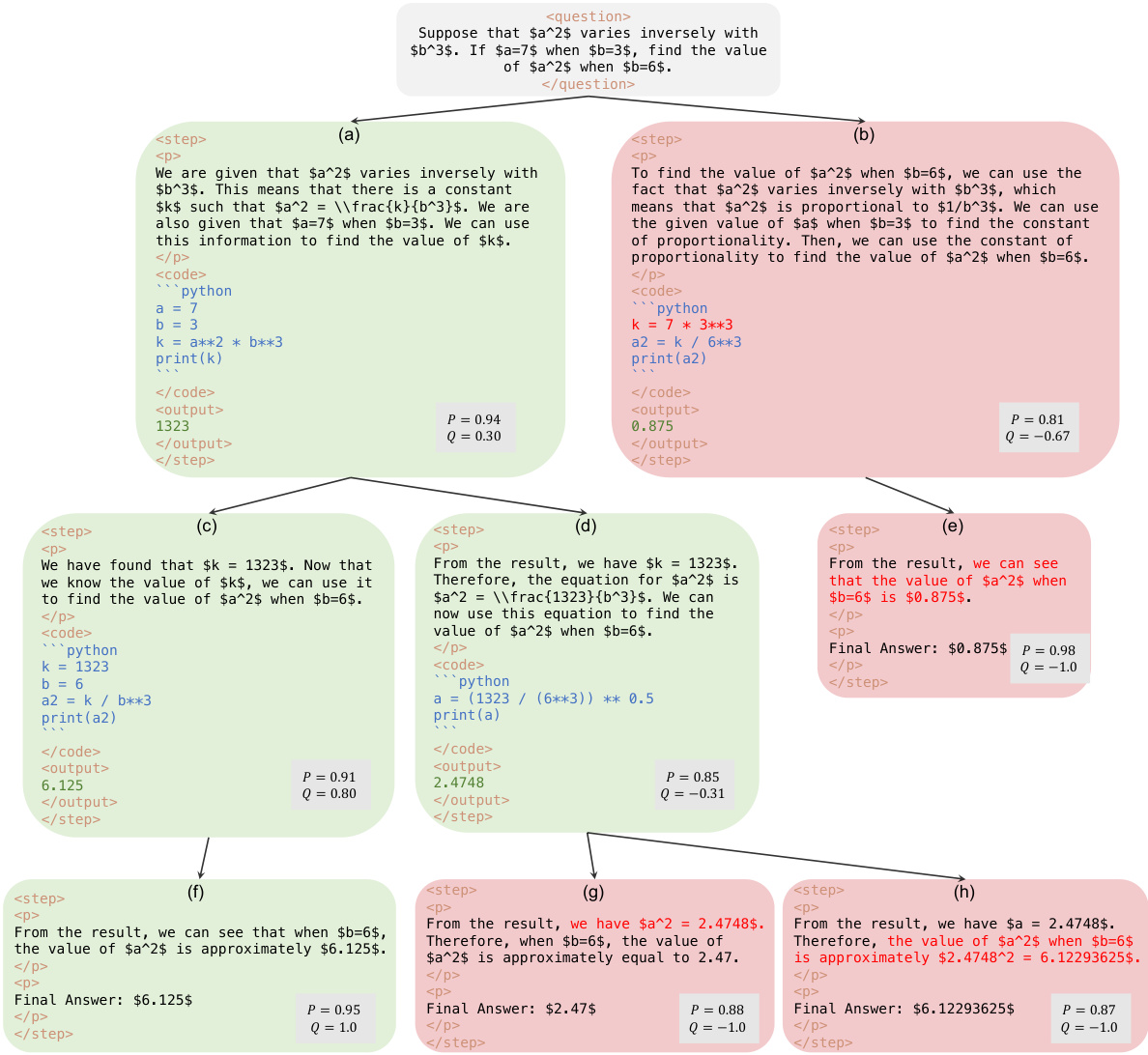
This figure illustrates the four key operations of the Monte Carlo Tree Search (MCTS) algorithm used in the AlphaMath framework. These steps are Selection, Expansion, Evaluation, and Backpropagation. Selection involves choosing a node based on a variant of the PUCT algorithm. Expansion involves expanding the selected leaf node, generating new partial solutions from the LLM. Evaluation involves assessing the leaf nodes using a value model or reward function. Backpropagation involves updating the Q-values and visit counts of the nodes along the path from the leaf node to the root.
This figure illustrates the iterative training process of the AlphaMath framework. It shows three main stages: data collection (question-answer pairs), MCTS application to generate solution paths with state values (both correct and incorrect), and model optimization using the generated data. The process is cyclical, with improved models feeding into subsequent iterations.
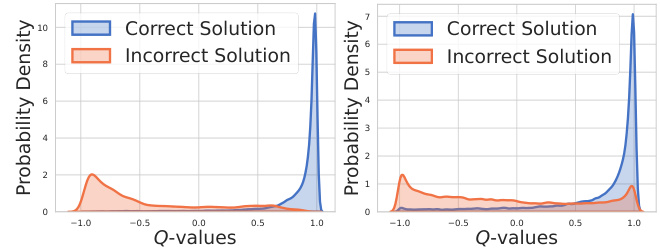
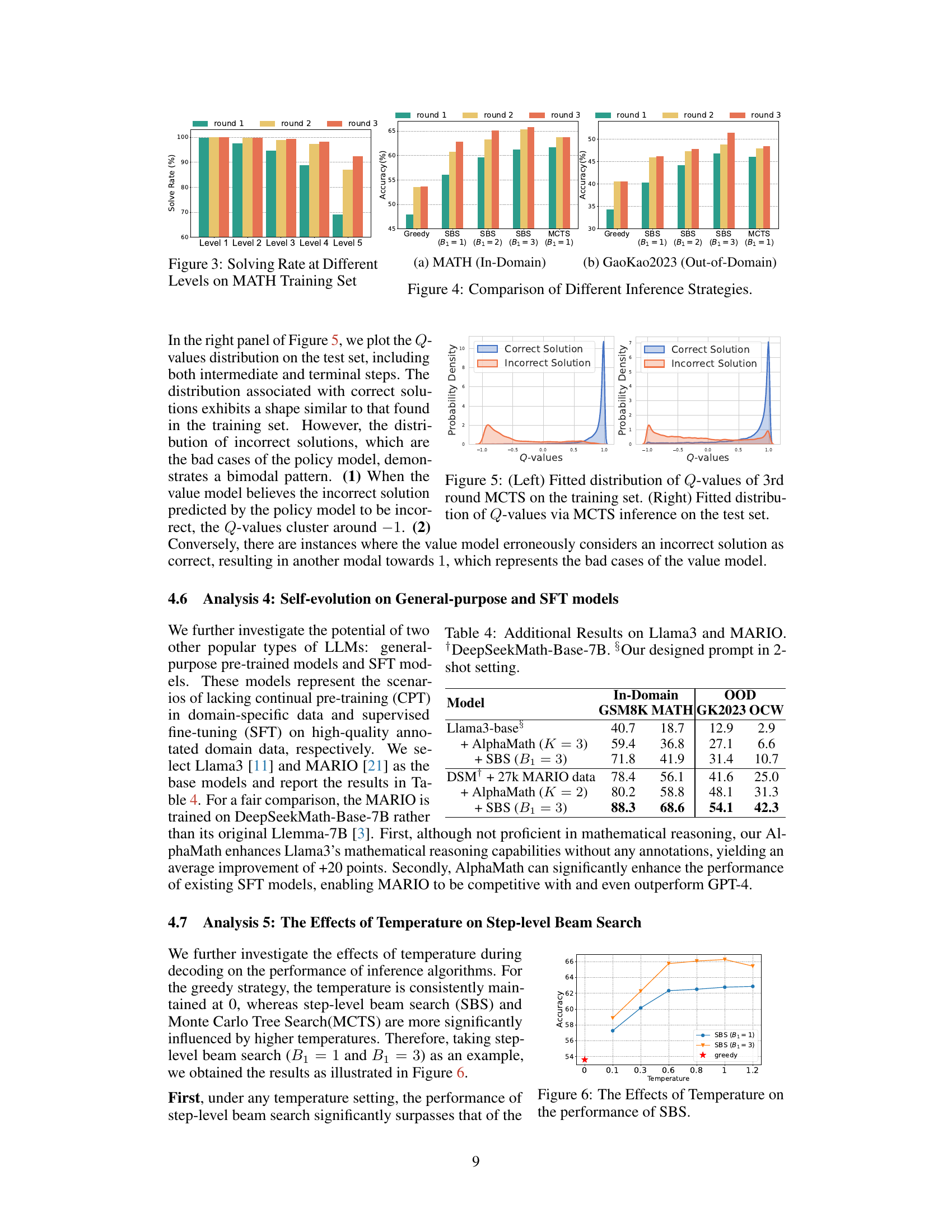
The figure shows the distribution of Q-values obtained from the Monte Carlo Tree Search (MCTS) algorithm. The left panel displays the distribution of Q-values from the training set in the third round of MCTS, while the right panel displays the distribution of Q-values obtained during MCTS inference on the test set. The distribution for correct solutions in both cases shows a strong skew towards a value of 1, while the distribution for incorrect solutions is more spread out with a smaller skew towards -1, which reflects how well the value model is able to distinguish between correct and incorrect solution paths.
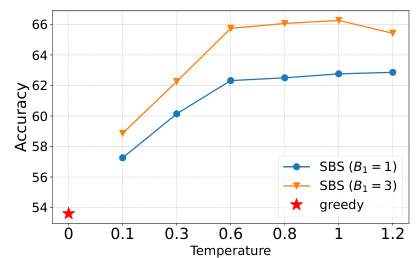
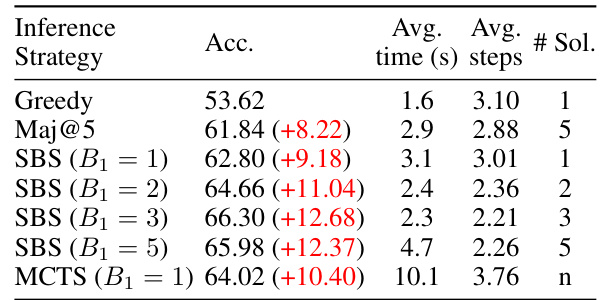
The figure shows the performance of step-level beam search (SBS) with different beam sizes (B1 = 1 and B1 = 3) under various temperature settings. The results are compared against a greedy approach. It demonstrates that SBS significantly outperforms the greedy approach across all temperatures, and that higher temperatures generally lead to better performance for SBS, although there are diminishing returns at the highest temperature.

This figure illustrates the iterative training process of the AlphaMath framework. The framework begins by collecting a dataset of mathematical questions and answers (Stage 1). Then, it uses Monte Carlo Tree Search (MCTS) along with a policy and value model to generate numerous solution paths, some correct and some incorrect, capturing the intermediate steps and their associated values (Stage 2). Finally, the policy and value models are jointly trained using this generated data, enabling them to learn effective mathematical reasoning strategies (Stage 3). This iterative process refines the models’ abilities to autonomously generate and evaluate high-quality solutions.
This figure illustrates the iterative training process of the AlphaMath framework. It begins with collecting a dataset of mathematical questions and answers. Then, the Monte Carlo Tree Search (MCTS) algorithm is used with the policy and value models to generate solution paths, which are labeled as correct or incorrect based on their final answers and given a state value. Finally, these generated paths and values are used to train and optimize the policy and value models, improving the accuracy of mathematical reasoning.
This figure illustrates the iterative training process of AlphaMath. It starts with collecting a dataset of mathematical questions and their answers. Then, it uses Monte Carlo Tree Search (MCTS) with a policy model (LLM) and a value model to generate many solution paths, some correct and some incorrect. Finally, it uses these generated paths and their associated state values to train and improve both the policy and value models. This iterative process helps AlphaMath learn to generate high-quality solutions without human-provided process annotations.

The figure illustrates the iterative training process of the AlphaMath framework. It begins with a mathematical dataset containing questions and answers (Stage 1). Then, Monte Carlo Tree Search (MCTS) is employed, using a policy model (LLM) and a value model to generate both correct and incorrect solution paths, along with their associated state values (Stage 2). Finally, these generated data (questions, solution paths, state values) are used to optimize both the policy and value models (Stage 3). This process is repeated iteratively to enhance the model’s mathematical reasoning abilities.

This figure illustrates the iterative training process of AlphaMath. It starts with a mathematical dataset containing questions and answers. Then, Monte Carlo Tree Search (MCTS) is used with a policy model (LLM) and a value model to generate solution paths, labeled as correct or incorrect based on their final answers. Finally, the policy and value models are jointly optimized using the generated data from the MCTS process.

This figure illustrates the iterative training process of the AlphaMath framework. The process involves three main stages: data collection, MCTS-based solution path generation, and model optimization. First, a dataset of mathematical questions and answers is collected. Then, Monte Carlo Tree Search (MCTS) is used in conjunction with a policy model (LLM) and value model to generate numerous solution paths, along with associated state values representing the quality of intermediate steps. Finally, these generated paths and values are used to iteratively train and refine both the policy and value models, improving the overall accuracy and effectiveness of mathematical reasoning.
This figure illustrates the iterative training process of the AlphaMath framework. It starts with a mathematical dataset containing questions and answers. Then, Monte Carlo Tree Search (MCTS) is used with a policy model (LLM) and a value model to generate solution paths, including both correct and incorrect ones, along with their associated state values. Finally, these generated data are used to optimize both the policy and value models. This iterative process refines the model’s ability to generate high-quality mathematical reasoning solutions.

This figure illustrates the iterative training process of AlphaMath. The process begins by collecting a mathematical dataset (questions and answers). Then, Monte Carlo Tree Search (MCTS) is used with a policy model (LLM) and a value model to generate correct and incorrect solution paths, along with associated state values. Finally, the policy and value models are optimized using the generated data from MCTS. This iterative process allows AlphaMath to generate high-quality process-supervised solutions without human intervention.
More on tables
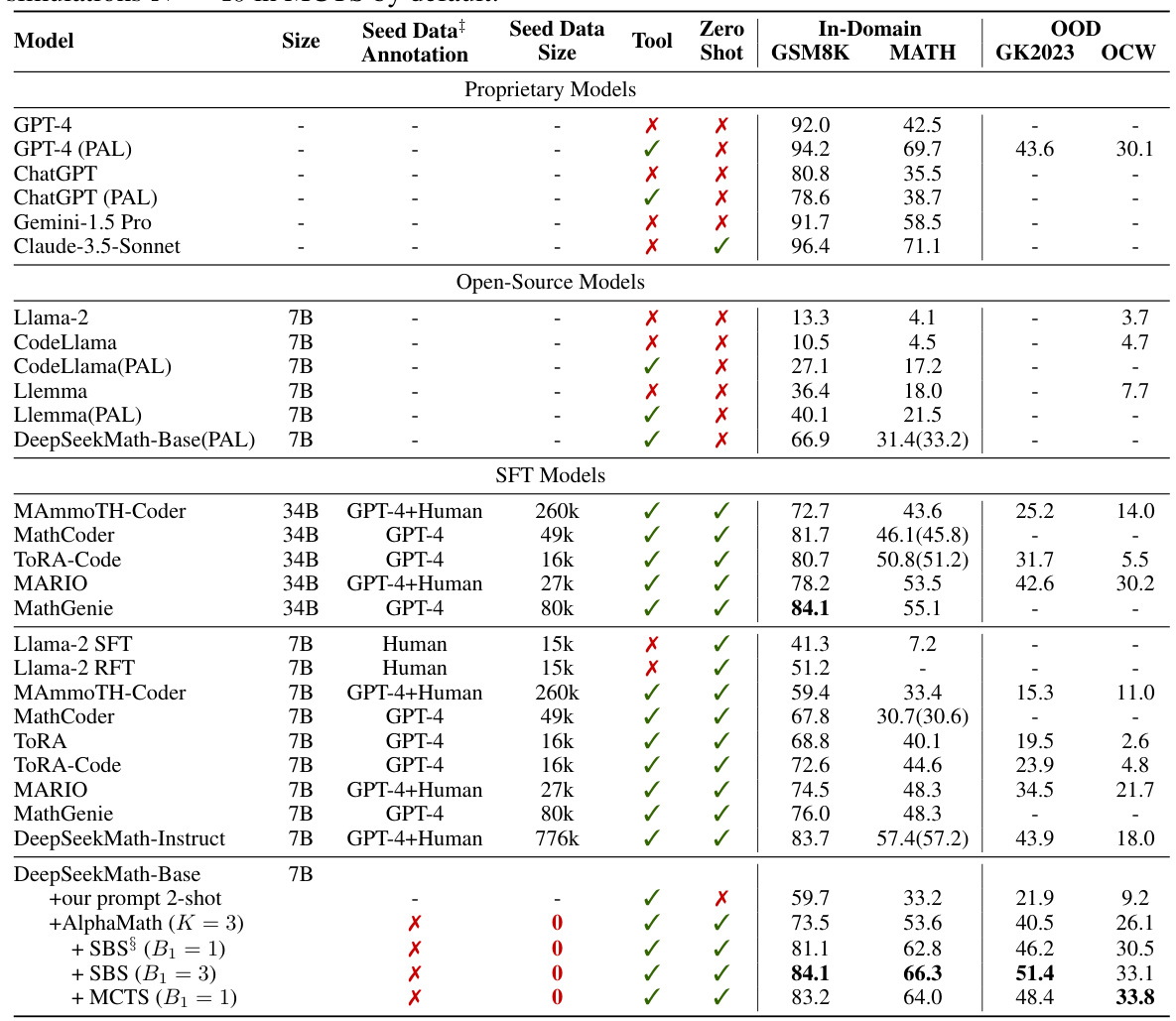
This table presents the main results of the AlphaMath model and compares its performance to various other models (proprietary, open-source, and fine-tuned) across several datasets. It includes metrics on both in-domain and out-of-domain datasets. The table specifies model size, the presence and type of seed data and annotation used for training, tools employed, and the performance metrics (accuracy) for each model and dataset. It also notes the use of specific techniques like step-level beam search (SBS) and Monte Carlo Tree Search (MCTS) for AlphaMath.
This table presents the main results of the AlphaMath model and compares its performance against various baselines on both in-domain and out-of-domain datasets. It shows the accuracy, along with the performance metrics (in brackets) obtained using an evaluation toolkit. The table also highlights the model size, whether seed data and external tools were used, and the specific inference strategies (SBS or MCTS) employed. It differentiates between proprietary and open-source models as well as SFT models. The best performing open-source models are bolded for easier readability.
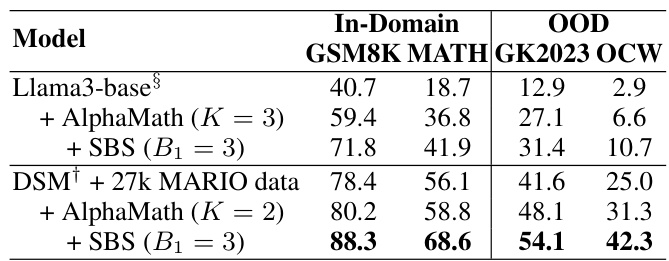
This table presents the main results of the AlphaMath model and compares its performance to various other models on both in-domain and out-of-domain datasets. It shows the model size, whether seed data (high-quality annotated question-solution pairs) was used, what tools were used (if any), and the accuracy scores on four datasets (GSM8K, MATH, GK2023, and OCW). The table highlights the performance gains achieved by AlphaMath, especially when combined with the step-level beam search (SBS) method, even without using seed data. Note that the performance with different inference strategies (greedy, SBS, and MCTS) is also included for the AlphaMath model.

This table presents the main results of the AlphaMath model and compares its performance with various other models on different mathematical reasoning datasets. It shows the accuracy of different models on in-domain (GSM8K, MATH) and out-of-domain (GaoKao2023, OCWCourses) datasets. The table also indicates whether each model uses process supervision (seed data), the size of the seed data, the tools used, and the model size. Finally, it highlights AlphaMath’s performance with and without MCTS and different beam search strategies, indicating the model’s capability even without high-quality, annotated data.

This table presents the main experimental results of the AlphaMath framework and compares its performance against various state-of-the-art methods on both in-domain and out-of-domain datasets. It shows the model size, the type and amount of training data used (including whether human or GPT-4 annotation was used), tools employed, and performance metrics on different datasets. The table highlights the performance of AlphaMath, especially its ability to achieve comparable or better results than existing models even without high-quality process-supervised data. It also includes the effect of different inference strategies (SBS, MCTS) and parameters.
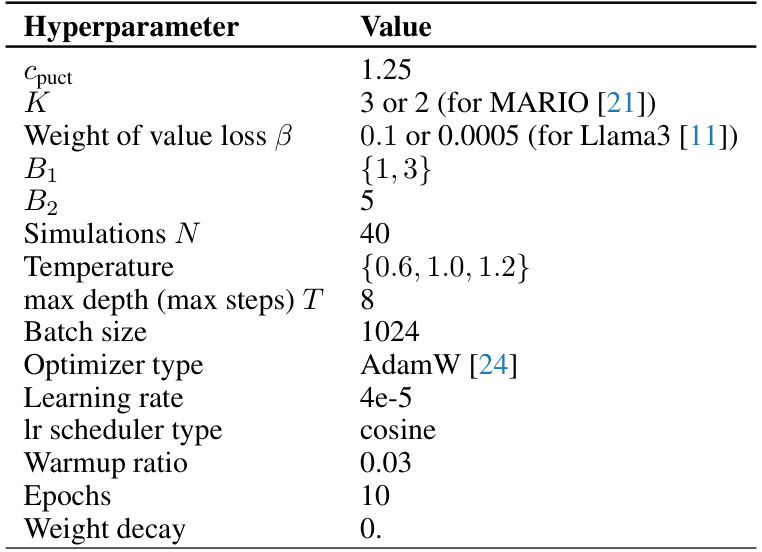
This table presents the main results of the experiments comparing AlphaMath with various state-of-the-art models on different datasets. It includes the model size, whether seed data was used, the annotation source, tool usage, performance on in-domain and out-of-domain datasets, and hyperparameters used in AlphaMath. The table highlights the performance of AlphaMath, particularly its ability to achieve comparable or superior results even without high-quality annotated data.
This table presents the main results of the AlphaMath model and compares its performance with various baselines on different mathematical reasoning datasets. It includes both in-domain and out-of-domain results for proprietary and open-source LLMs, as well as LLMs fine-tuned with process supervision. The table details the model size, the use of seed data (high-quality annotated data), the tools used, and the performance metrics (accuracy) on various datasets (GSM8K, MATH, GaoKao2023, and OCWCourses). Different versions of the AlphaMath model are shown, highlighting the effect of using Monte Carlo Tree Search (MCTS) or the more efficient Step-level Beam Search (SBS) and the impact of the number of iterations in training.
Full paper#