↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many reinforcement learning (RL) applications use heuristic rewards alongside task rewards to guide learning and improve performance. However, existing methods often fail to outperform heuristic-only policies, especially with limited data, due to their focus on ‘optimal policy invariance’. This invariance guarantees convergence to the best policy given infinite data, but doesn’t ensure better performance with limited data.
This paper introduces Heuristic-Enhanced Policy Optimization (HEPO), a novel method that addresses this limitation. HEPO directly enforces the policy improvement condition, ensuring that the trained policy always outperforms the heuristic-only policy. Experiments demonstrate that HEPO consistently outperforms heuristic-only policies across various robotic control tasks, showcasing its effectiveness even with suboptimal heuristics and limited data.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with heuristic rewards in reinforcement learning. It challenges the existing paradigm of optimal policy invariance, offering a novel constrained optimization approach that consistently improves task performance even with limited data. This work opens new avenues for more efficient and reliable RL training with heuristics, particularly in complex robotic applications.
Visual Insights#
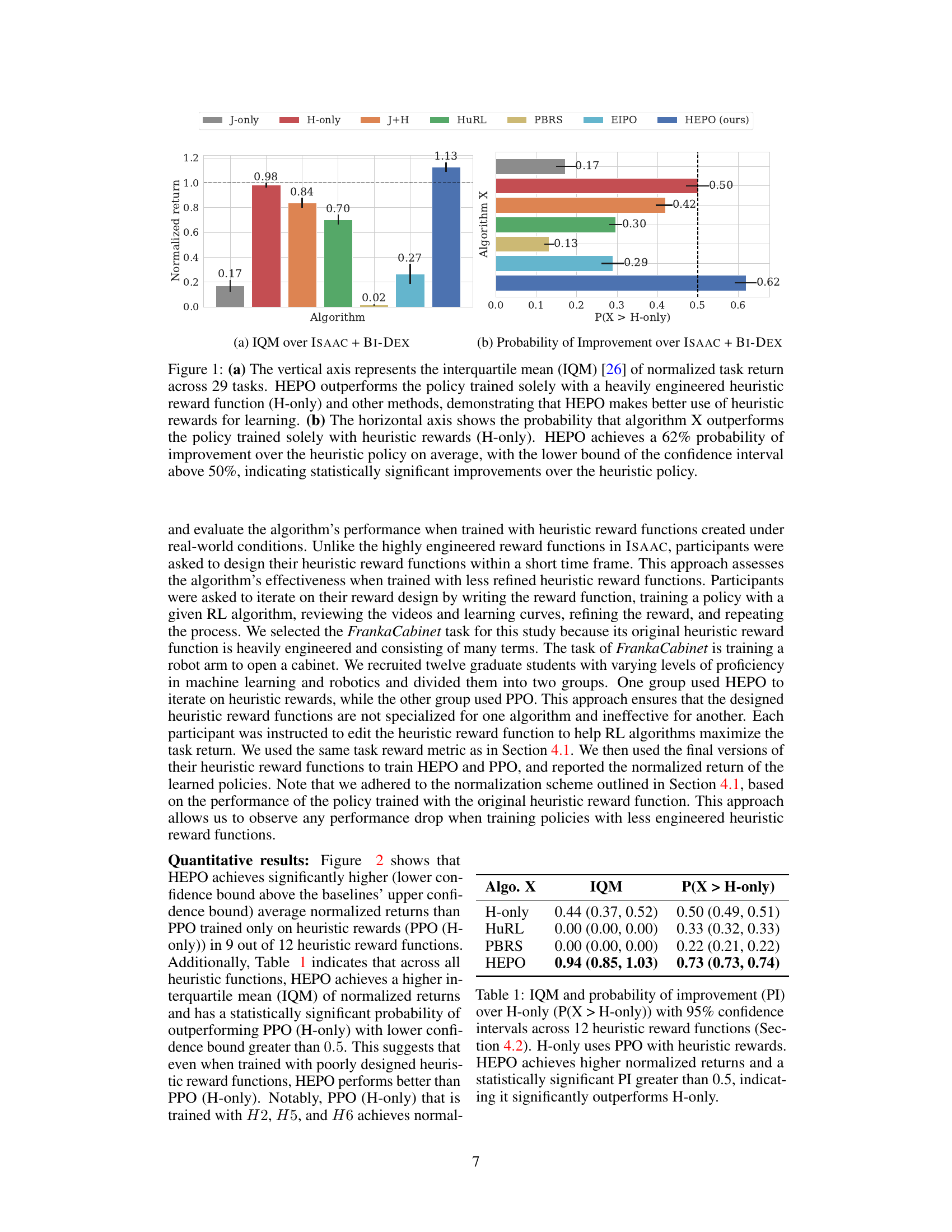
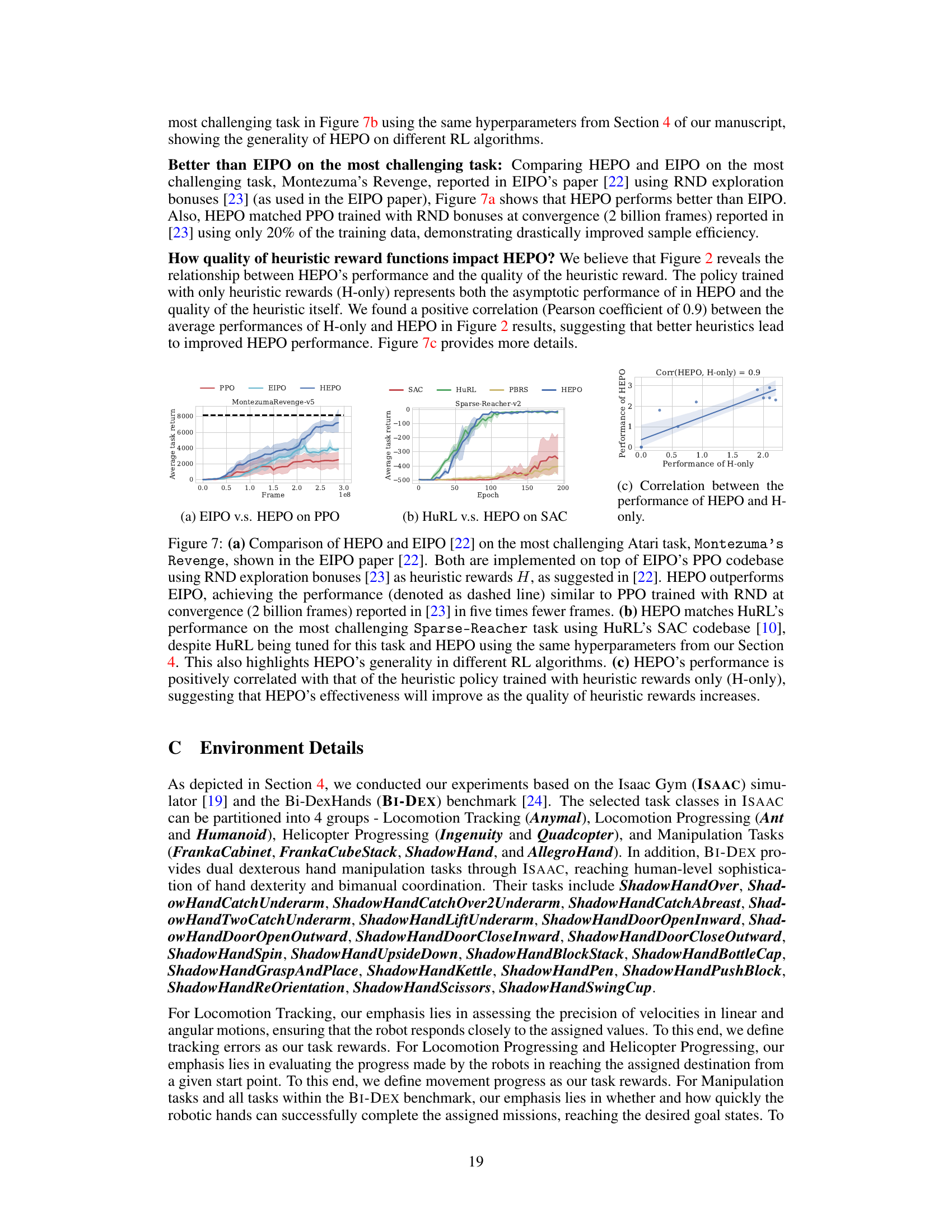
This figure compares the performance of HEPO against several baselines across 29 tasks. Subfigure (a) shows the interquartile mean (IQM) of the normalized task return for each algorithm, demonstrating that HEPO significantly outperforms the other methods, particularly the ‘H-only’ (heuristic-only) baseline. Subfigure (b) shows the probability that each algorithm outperforms the H-only baseline, with HEPO showing a probability of improvement greater than 50%, indicating statistical significance.

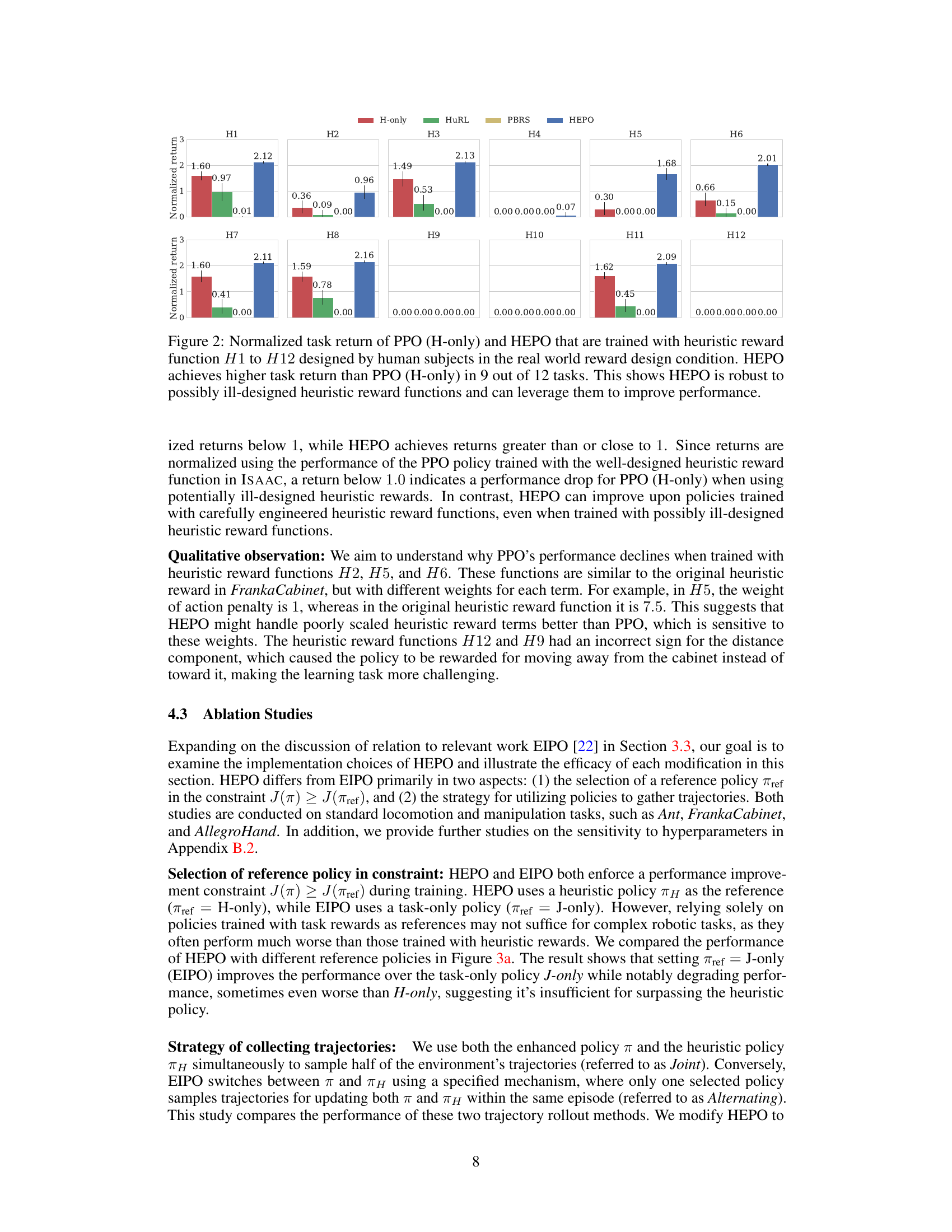
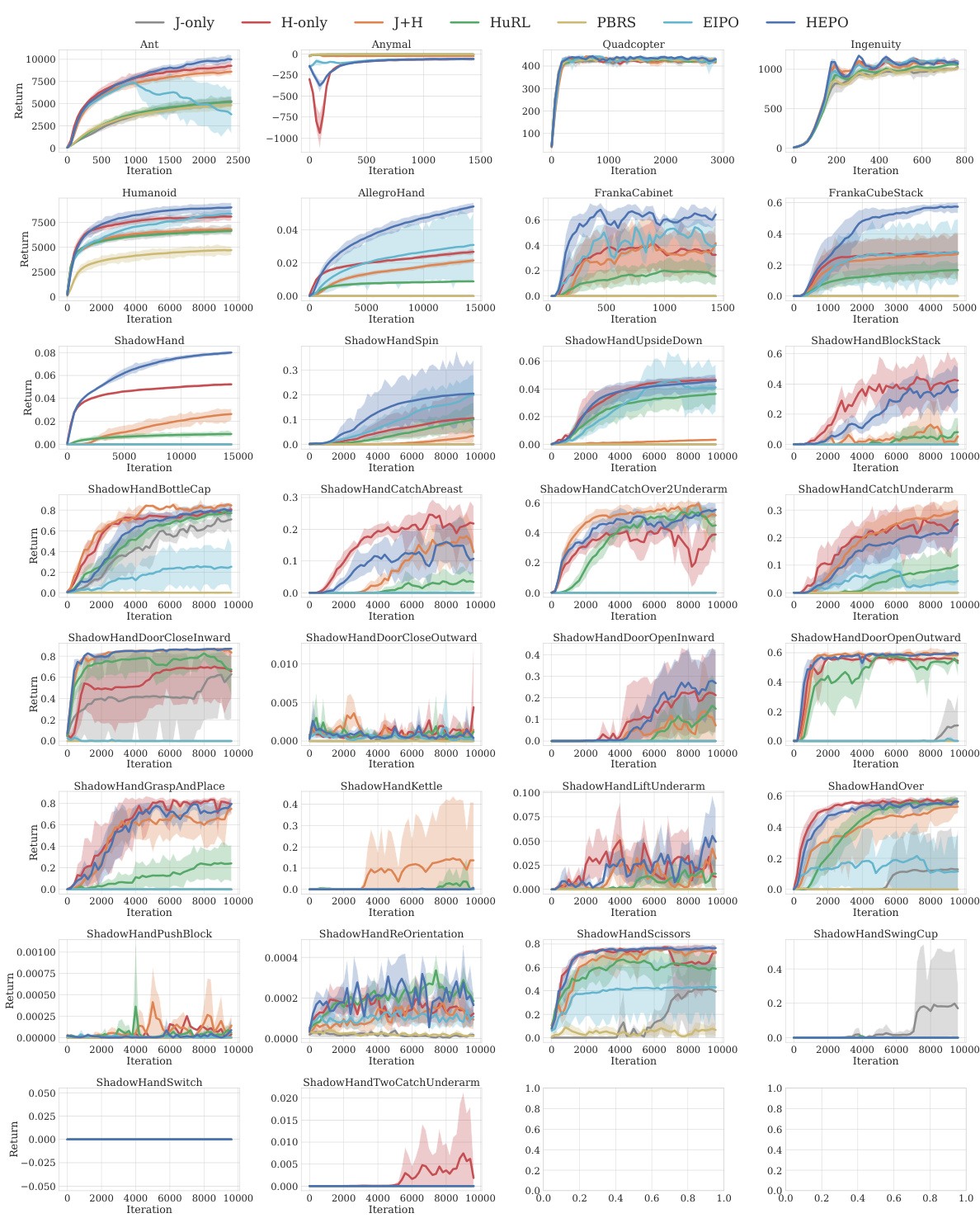
This table presents a comparison of the performance of different algorithms on 12 tasks with heuristic reward functions created by human participants. The algorithms are evaluated using two metrics: the interquartile mean (IQM) of normalized task returns and the probability of improvement (PI) over the heuristic-only baseline (H-only). The results show that HEPO consistently outperforms H-only, demonstrating its robustness and effectiveness in utilizing heuristic rewards.
In-depth insights#
Heuristic Policy Limits#
The use of heuristics in reinforcement learning, while often improving performance with limited data, presents significant limitations. Heuristics, by definition, represent suboptimal strategies. They encode human assumptions and biases, potentially restricting the exploration of superior policies that deviate from human intuition. Over-reliance on heuristics can lead to premature convergence on locally optimal solutions, preventing the discovery of globally optimal policies. Furthermore, the effectiveness of heuristics is highly dependent on their quality and design; poorly designed heuristics can severely hinder performance or even lead to a suboptimal agent. Therefore, incorporating heuristics requires careful consideration of the trade-off between faster initial learning and the risk of limiting the agent’s ability to discover truly optimal solutions. Balancing heuristic rewards with task rewards is crucial, requiring careful tuning that can be time-consuming and task-specific. A key challenge is to ensure that heuristics serve as valuable guides rather than limiting constraints.
Constrained Optimization#
The concept of constrained optimization, applied within the context of reinforcement learning using heuristic rewards, presents a powerful approach to overcome limitations of standard reward shaping methods. The core idea is to constrain the optimization process, ensuring that the learned policy consistently outperforms a heuristic-only policy. This addresses the common issue where policies might exploit heuristic rewards without improving task performance. By imposing this constraint, the algorithm is effectively forced to leverage heuristics only when it genuinely helps achieve a better task-oriented outcome. This approach avoids the need for manual tuning of reward weights, a significant advantage over conventional methods. The introduction of a Lagrangian multiplier facilitates a dynamic balance between task and heuristic rewards throughout the training process, thereby enabling adaptive weighting based on policy improvement rather than relying on predefined constants. This constrained optimization methodology offers a robust solution for diverse applications, particularly in scenarios with limited data or noisy reward signals, enhancing the reliability and efficiency of reinforcement learning techniques.
HEPO Algorithm#
The HEPO algorithm tackles the challenge of effectively integrating heuristic rewards into reinforcement learning (RL) without compromising optimal task performance. Instead of seeking optimal policy invariance, which can fail with limited data, HEPO imposes a constraint that the learned policy consistently outperforms a heuristic-only baseline. This constraint is implemented using a Lagrangian multiplier, adaptively balancing task and heuristic rewards based on the current policy’s performance. This adaptive approach avoids the often time-consuming and problem-specific task of manually tuning reward weights. The effectiveness of HEPO is demonstrated across multiple robotic control tasks. Crucially, HEPO shows robustness to the quality of the heuristic rewards, maintaining performance improvements even when heuristic signals are poorly designed or only somewhat helpful. This makes HEPO a valuable tool for RL practitioners, potentially reducing development time by making heuristic rewards more easily deployable and reliable.
Reward Function Design#
Reward function design is crucial in reinforcement learning, significantly impacting the agent’s learning process and overall performance. A poorly designed reward function can lead to unintended behavior, suboptimal solutions, or even catastrophic failures. Careful consideration of the reward’s components, their scaling, and potential biases is necessary. For example, sparse rewards might make learning inefficient, while dense rewards might make the agent focus on easier sub-goals instead of the main objective. This often requires a delicate balance between shaping rewards to guide the agent efficiently towards a solution and avoiding unwanted behavior arising from reward hacking. Effective reward design often involves iterative refinement, starting with a simple reward function, observing the agent’s behavior, and adjusting the reward based on the observations. Human expertise and prior knowledge can guide the process, suggesting useful heuristic reward terms that can be incorporated to improve learning efficiency and performance. However, this also necessitates methods to ensure that such heuristic rewards do not limit the potential of the RL agent to discover better solutions than those implied by the heuristics. Therefore, constraint-based approaches that balance heuristic guidance with the pursuit of optimal task performance become critical for effective reward design. This ensures that the agent’s focus remains on optimizing the true task objective while utilizing the heuristic reward to improve efficiency.
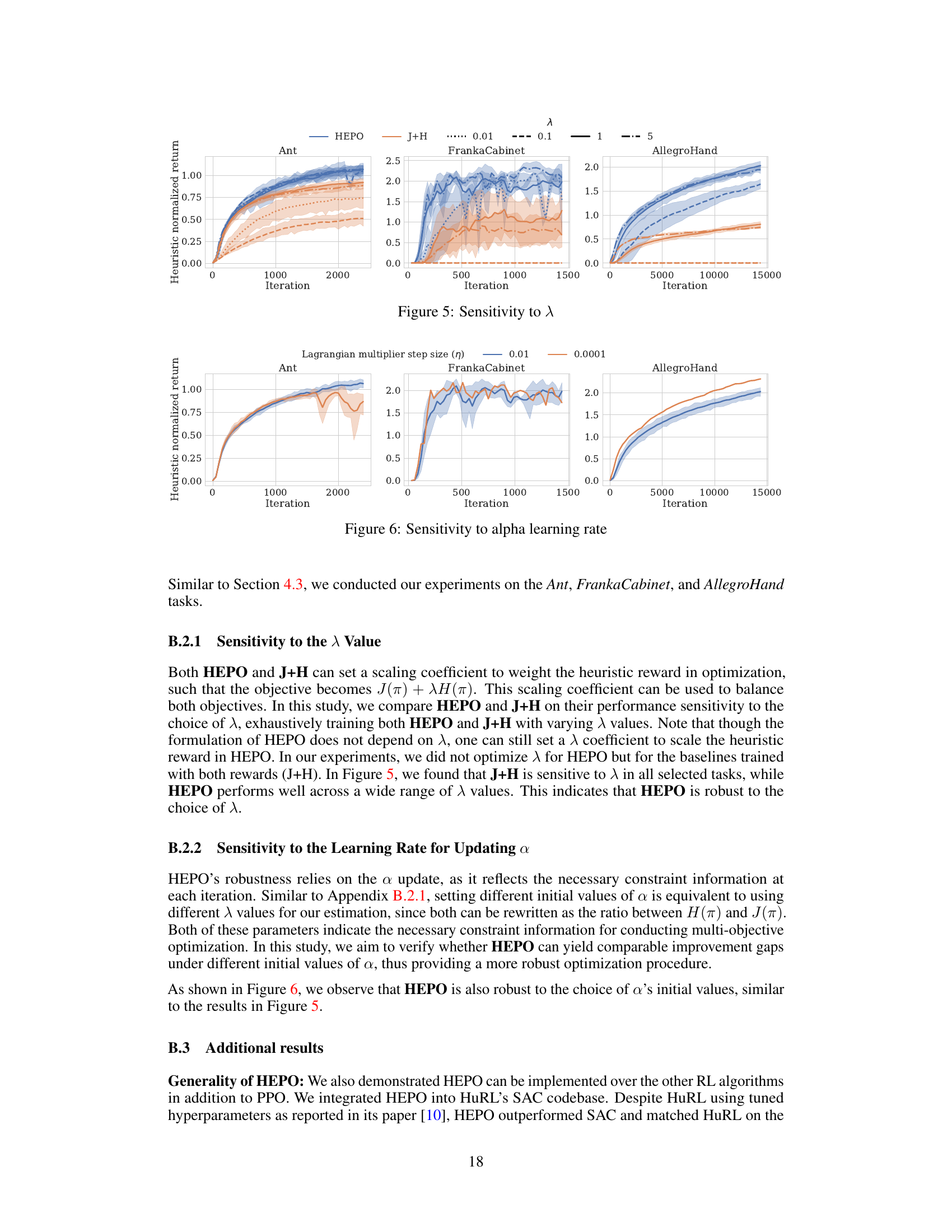
Ablation Studies#
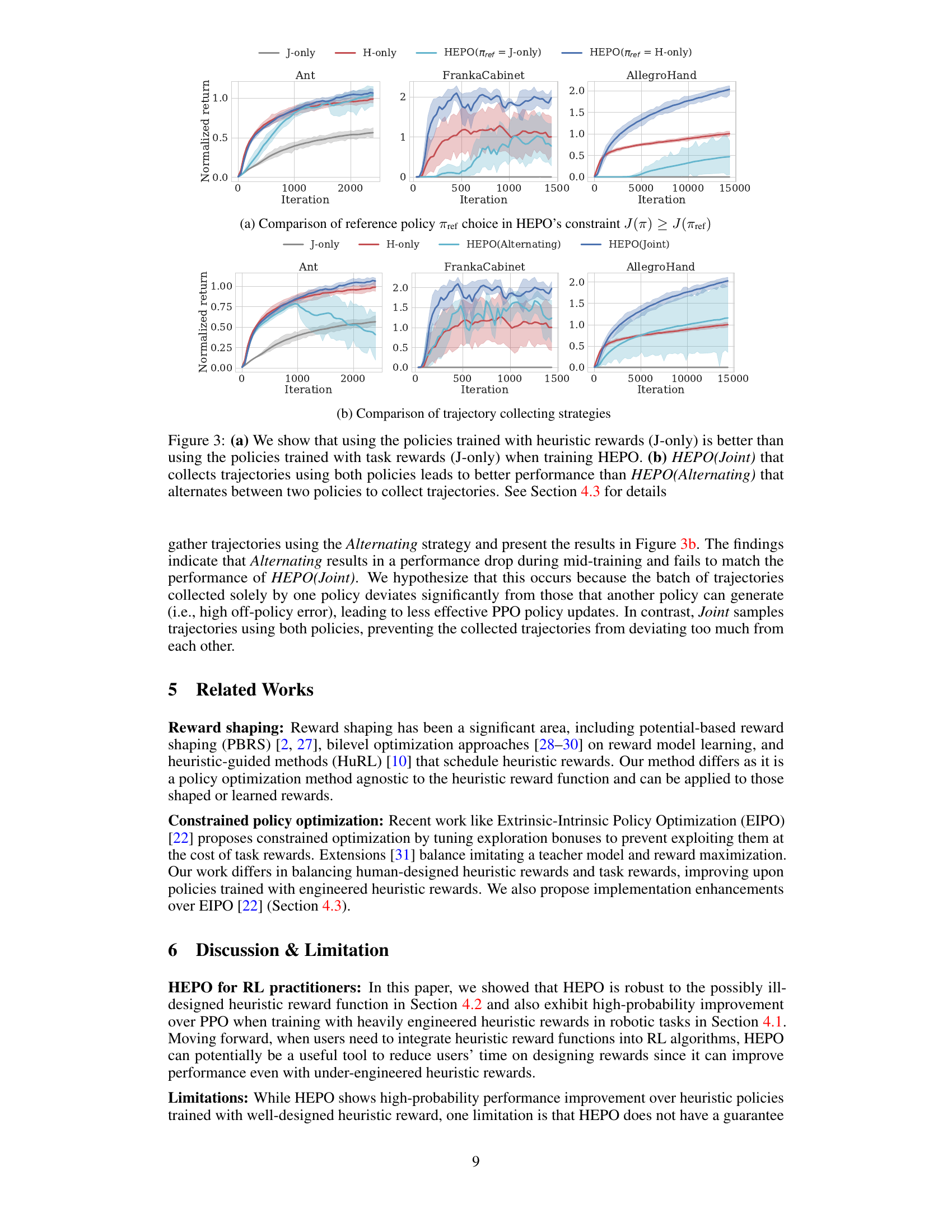
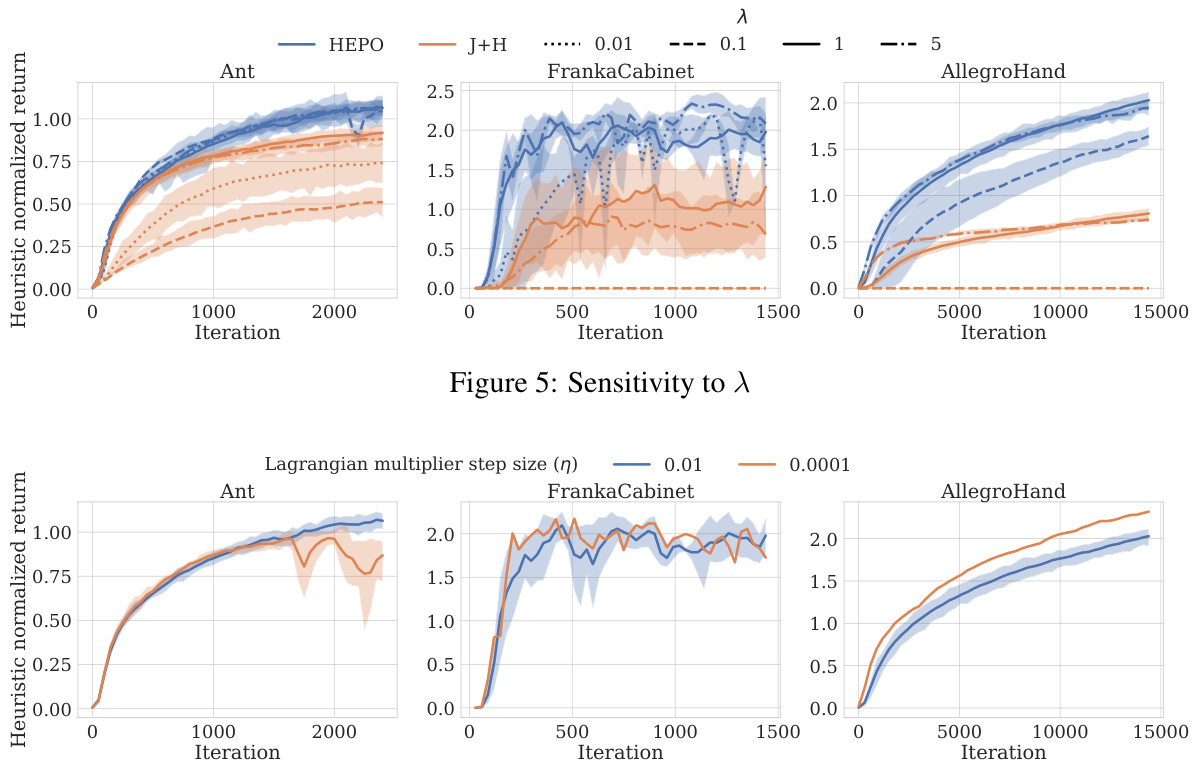
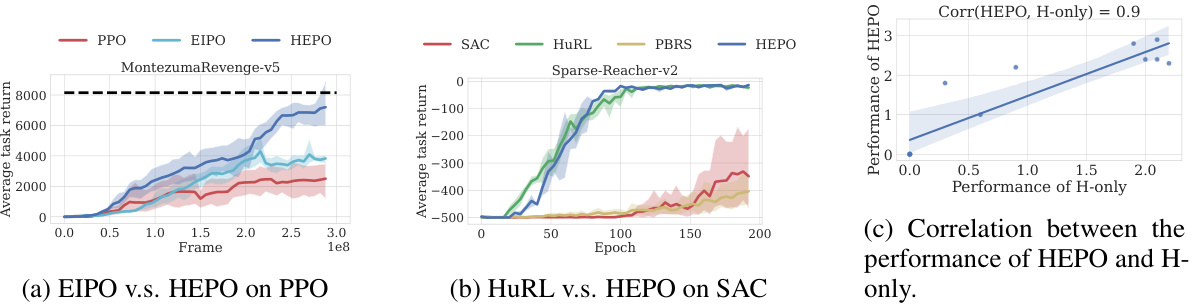
Ablation studies systematically remove components of a model to assess their individual contributions. In this context, it would likely involve removing or modifying aspects of the proposed method (e.g., the constraint, the Lagrangian multiplier update, the policy training approach) to understand their effects on performance. Key findings from these experiments would pinpoint whether the policy improvement constraint, adaptive reward weighting via the Lagrangian multiplier, or the joint trajectory collection strategy are essential for the improved performance. The results would be crucial for demonstrating the necessity and effectiveness of the design choices, clarifying what aspects provide the most significant improvements and helping to determine the overall robustness of the method. Comparison to related approaches, such as Extrinsic-Intrinsic Policy Optimization (EIPO), will also offer valuable insights into the unique advantages of the proposed technique.
More visual insights#
More on figures

This figure compares the performance of different reinforcement learning algorithms on 29 robotic tasks. Panel (a) shows the interquartile mean (IQM) of normalized task return, illustrating that HEPO significantly outperforms algorithms trained solely on heuristic rewards or those that attempt to balance heuristic and task rewards. Panel (b) displays the probability that each algorithm outperforms the heuristic-only approach, highlighting HEPO’s superior performance with a probability exceeding 50%. The results strongly suggest that HEPO’s method for incorporating heuristic rewards is more effective than existing methods.

This figure presents a comparison of the performance of different RL algorithms, including the proposed HEPO method, on various robotic tasks. Panel (a) shows the interquartile mean (IQM) of normalized task returns, demonstrating HEPO’s superior performance compared to other methods. Panel (b) displays the probability of improvement, indicating HEPO significantly outperforms policies trained only on heuristic rewards. This showcases HEPO’s effectiveness in utilizing heuristic information while prioritizing the task objective, even with limited data.

This figure presents ablation study results comparing two key design choices in the HEPO algorithm: (a) the reference policy used in the constraint J(π) ≥ J(πref) and (b) the strategy for collecting trajectories (Joint vs. Alternating). Subfigure (a) shows that using the heuristic policy as the reference policy yields better performance than using the task-only policy in the constraint. Subfigure (b) demonstrates that concurrently collecting trajectories using both the enhanced policy and the heuristic policy (Joint) leads to better performance than alternating between policies for trajectory collection.
This figure compares the performance of HEPO against other baseline methods across 29 benchmark tasks. The interquartile mean (IQM) of normalized task return shows that HEPO outperforms other methods, particularly the H-only baseline which uses only a heuristic reward. The probability of improvement metric further confirms that HEPO significantly outperforms the H-only baseline, indicating the effectiveness of its policy improvement constraint.
This figure shows a comparison of different reinforcement learning algorithms on 29 robotic tasks. The algorithms are compared based on their normalized task return (a measure of how well they perform on the task relative to a baseline and a random policy) and the probability that they outperform a heuristic-only policy. HEPO significantly outperforms other methods including classic methods that ensure optimal policy invariance which shows theoretical guarantees but fails in practice. HEPO consistently improves performance compared to a baseline that uses only heuristic rewards, indicating its robustness and effectiveness in leveraging heuristic rewards to improve task performance.
This figure displays the results of experiments comparing HEPO’s performance to other baselines on 29 tasks. Subfigure (a) shows the interquartile mean (IQM) of normalized task return for all algorithms, demonstrating that HEPO achieves the best performance. Subfigure (b) shows that HEPO outperforms the H-only policy (trained solely on heuristic rewards) with a 62% probability of improvement and a lower bound of the confidence interval above 50%, indicating a statistically significant improvement.
This figure presents a comparison of different reinforcement learning algorithms on 29 robotic tasks. The algorithms are tested using both task and heuristic rewards. Panel (a) shows the interquartile mean (IQM) of normalized task return, demonstrating HEPO’s superior performance compared to other algorithms, especially when using heavily engineered heuristic rewards. Panel (b) illustrates the probability of each algorithm outperforming the heuristic-only policy, highlighting that HEPO significantly surpasses the heuristic-only policy in most cases (62% probability, with confidence interval’s lower bound above 50%).
This figure presents a comparison of different reinforcement learning algorithms on 29 robotic tasks. Figure 1(a) shows the Interquartile Mean (IQM) of the normalized task return for each algorithm, demonstrating HEPO’s superior performance compared to methods using only heuristic rewards (H-only), heuristic rewards with optimal policy invariance (PBRS), or a mixture of task and heuristic rewards (J+H). Figure 1(b) further highlights HEPO’s statistical significance, showing a greater than 50% probability of outperforming the H-only baseline across tasks. This indicates that HEPO effectively leverages heuristic rewards without sacrificing task performance.
This figure presents a comparison of different reinforcement learning methods for solving robotic tasks using heuristic rewards. The left panel shows the interquartile mean (IQM) of the normalized task return for several methods, highlighting HEPO’s superior performance. The right panel displays the probability of each method outperforming the heuristic-only approach, further demonstrating HEPO’s significant improvement.

This figure compares the performance of HEPO against other methods across 29 tasks from the ISAAC and BI-DEX benchmarks. The left panel shows the interquartile mean (IQM) of normalized task return, demonstrating that HEPO significantly outperforms other methods, including one trained solely with heuristic rewards. The right panel shows the probability of HEPO outperforming the heuristic-only policy, further highlighting HEPO’s superior performance and statistical significance (probability exceeding 50%).

This figure compares the performance of HEPO against other methods in terms of normalized task return and probability of improvement over the heuristic-only policy. The interquartile mean (IQM) of normalized task return is shown in (a), indicating HEPO’s superior performance. The probability of improvement is shown in (b), showing that HEPO outperforms the heuristic-only policy in over 62% of the tasks, achieving statistical significance.

This figure presents a comparison of the performance of different reinforcement learning algorithms across 29 tasks. Part (a) shows the interquartile mean (IQM) of normalized task return. HEPO consistently outperforms other methods, indicating effective use of heuristic rewards. Part (b) shows the probability of each algorithm outperforming a heuristic-only policy. HEPO significantly surpasses the heuristic-only policy, demonstrating substantial improvement.

This figure displays a comparison of the performance of different reinforcement learning algorithms on 29 robotic tasks. The algorithms are evaluated based on two metrics: the interquartile mean (IQM) of the normalized task return and the probability of improvement over the heuristic policy. The results show that HEPO outperforms other algorithms in both metrics, indicating a statistically significant improvement in task performance. This improvement is consistent across a wide range of tasks and regardless of the heuristic rewards quality.
This figure presents a comparison of different reinforcement learning algorithms’ performance in maximizing task rewards when trained with heuristic rewards. Subfigure (a) shows the interquartile mean (IQM) of normalized task returns, indicating HEPO’s superior performance compared to other methods, including those using only task rewards (J-only) or only heuristic rewards (H-only). Subfigure (b) displays the probability of improvement for each algorithm compared to H-only, revealing that HEPO has a 62% chance of outperforming the heuristic-only policy, statistically significant due to the lower confidence bound exceeding 50%. This demonstrates HEPO’s effectiveness in leveraging heuristic rewards to enhance task performance in a finite-data setting.

This figure shows the results of comparing HEPO against several baselines across 29 robotic tasks. The interquartile mean (IQM) of the normalized task return for HEPO is significantly higher than for the other baselines. The probability of HEPO outperforming the heuristic-only policy is 62%, which is statistically significant.

This figure presents a comparison of the performance of HEPO against other baseline methods on 29 robotic tasks. The interquartile mean (IQM) of the normalized task return shows HEPO’s superiority. Additionally, HEPO demonstrates a greater than 50% probability of improving upon the heuristic-only policy, showcasing statistically significant performance gains.

This figure shows the results of comparing HEPO with other methods. The left panel (a) presents the interquartile mean (IQM) of the normalized task return across 29 tasks, demonstrating that HEPO outperforms other methods, especially H-only (heuristic-only). The right panel (b) shows that HEPO has a high probability (62%) of outperforming H-only, indicating statistically significant improvement.

This figure presents a comparison of the performance of different reinforcement learning algorithms, including the proposed HEPO method, across various robotic manipulation tasks. Panel (a) shows the interquartile mean (IQM) of the normalized task return, indicating that HEPO consistently outperforms the other methods, particularly the H-only baseline which uses only heuristic rewards. Panel (b) displays the probability of each algorithm outperforming the H-only baseline, highlighting HEPO’s significantly higher success rate (62%). The results demonstrate HEPO’s effectiveness in leveraging heuristic rewards to improve task performance, even surpassing policies trained solely on engineered heuristics.

This figure presents a comparison of different reinforcement learning algorithms in terms of their performance on 29 tasks. The performance is measured using the interquartile mean (IQM) of normalized task return and the probability of improvement over a baseline policy trained only with heuristic rewards. HEPO, the proposed algorithm, consistently outperforms the baseline and other algorithms in both measures, indicating its effectiveness in leveraging heuristic rewards for improved task performance.

This figure displays a comparison of different reinforcement learning algorithms in terms of their performance on 29 tasks. The interquartile mean (IQM) of normalized task returns shows that HEPO significantly outperforms other methods, particularly the H-only baseline. Further, the probability of improvement metric highlights HEPO’s ability to surpass heuristic-only policies with a statistically significant probability (greater than 50%).

This figure presents a comparison of different reinforcement learning algorithms on 29 robotic tasks. The interquartile mean (IQM) of normalized task return shows that HEPO significantly outperforms other algorithms, including one trained only with heuristic rewards. Additionally, the probability of HEPO’s performance exceeding that of the heuristic-only algorithm is 62%, with a lower confidence bound above 50%, indicating statistical significance.

This figure presents the results comparing HEPO with several baseline methods. Subfigure (a) shows the interquartile mean (IQM) of normalized task return for each method. HEPO consistently achieves higher returns compared to baselines (especially H-only, which uses only heuristic rewards). Subfigure (b) displays the probability of improvement; HEPO significantly outperforms H-only in most of the tasks. This indicates that HEPO’s constraint for policy improvement is effective and robust even with finite data and potentially poor heuristic rewards.

This figure displays a comparison of the performance of different reinforcement learning algorithms, including HEPO, on 29 tasks. Panel (a) uses interquartile mean (IQM) of normalized task return to show HEPO’s superior performance compared to baselines (H-only, J-only, J+H, HuRL, PBRS, EIPO). Panel (b) shows the probability that each algorithm outperforms the H-only baseline, demonstrating that HEPO significantly outperforms the heuristic policy.

This figure presents a comparison of different reinforcement learning algorithms on 29 tasks using two metrics: interquartile mean (IQM) of normalized return and probability of improvement over the heuristic-only policy. The results show that HEPO consistently outperforms other methods, demonstrating its effectiveness in leveraging heuristic rewards to enhance task performance.

This figure displays a comparison of different reinforcement learning algorithms’ performance on 29 robotic tasks. Part (a) shows the interquartile mean (IQM) of normalized task return, indicating HEPO’s superior performance compared to other methods, including those trained with only heuristic rewards or a mixture of task and heuristic rewards. Part (b) presents the probability of each algorithm outperforming the heuristic-only policy, highlighting HEPO’s statistically significant (over 50%) improvement.

This figure shows the results of experiments comparing HEPO against several baselines across 29 tasks. Part (a) displays the interquartile mean (IQM) of normalized task return, showing HEPO significantly outperforms other methods, particularly those using only heuristic rewards. Part (b) illustrates the probability of improvement, indicating that HEPO outperforms the heuristic-only policy in over 60% of the tasks, a statistically significant result.

This figure shows the comparison of HEPO with other methods in terms of the Interquartile Mean (IQM) of normalized task return and the probability of improvement over the heuristic policy on 29 tasks. HEPO significantly outperforms other methods in both metrics, indicating its effectiveness in utilizing heuristic rewards for improved task performance.

This figure displays a comparison of different reinforcement learning algorithms on 29 tasks. The first subfigure (a) shows the Interquartile Mean (IQM) of the normalized task return for each algorithm; HEPO significantly outperforms all other methods. The second subfigure (b) shows the probability that each algorithm outperforms the heuristic-only policy; HEPO shows a statistically significant improvement (above 50%).

This figure presents a comparison of different reinforcement learning algorithms on 29 robotic tasks. The interquartile mean (IQM) of normalized task returns shows that HEPO significantly outperforms other methods, including those using only heuristic rewards or a mixture of task and heuristic rewards. The probability of improvement plot further demonstrates that HEPO has a statistically significant advantage over the heuristic-only policy. This indicates HEPO’s effectiveness in utilizing heuristic rewards to improve task performance.
More on tables
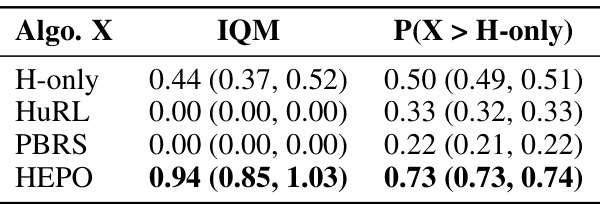
This table presents a comparison of the performance of different reinforcement learning algorithms on 12 tasks. The algorithms are evaluated based on two metrics: the interquartile mean (IQM) of normalized task return and the probability of improvement (PI) over a baseline algorithm trained only with heuristic rewards (H-only). The results demonstrate that the HEPO algorithm significantly outperforms the baseline and other compared methods, showcasing its robustness and effectiveness.

This table lists the hyperparameters specifically used for the Heuristic-Enhanced Policy Optimization (HEPO) algorithm in the paper’s experiments. It includes the initial value of the Lagrangian multiplier (α), the learning rate for updating α, the clipping range applied to the α updates to prevent instability, and the allowed range of α values.

This table presents the results of comparing HEPO’s performance against a baseline (H-only) across 12 heuristic reward functions. The interquartile mean (IQM) of normalized task returns and the probability of improvement (PI) are shown, along with 95% confidence intervals. The results demonstrate that HEPO consistently outperforms the H-only baseline.

This table presents a quantitative comparison of HEPO against the H-only baseline and other algorithms. The comparison uses two metrics: the Interquartile Mean (IQM) of normalized task returns, a robust measure of central tendency, and the probability of improvement (PI) over the H-only baseline, indicating the frequency with which HEPO outperforms the H-only policy. The results show HEPO’s statistical significance in improving performance.

This table presents the results of a comparison between HEPO and the H-only baseline across 12 heuristic reward functions. The results are presented in terms of Interquartile Mean (IQM) of normalized task return and the probability of improvement (PI) over H-only, both with 95% confidence intervals. The results show that HEPO significantly outperforms H-only.

This table presents a quantitative comparison of different reinforcement learning algorithms on 12 heuristic reward functions. The Interquartile Mean (IQM) of normalized task returns and the probability of improvement over a heuristic-only baseline (H-only) are reported for each algorithm, along with 95% confidence intervals. The results show that HEPO consistently outperforms the heuristic-only baseline, achieving statistically significant improvements.

This table presents the results of an experiment comparing different RL algorithms on 12 heuristic reward functions. The interquartile mean (IQM) of normalized task return and the probability of improvement over the heuristic-only policy (H-only) are reported for each algorithm, along with 95% confidence intervals. HEPO consistently outperforms other methods.
Full paper#