↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Logistic regression is a vital tool in machine learning, but minimizing its associated logistic loss can be computationally expensive for large datasets. This paper focuses on the space complexity of efficiently approximating this loss, a problem addressed by using coresets – smaller data subsets that approximate the original data. Prior work showed that coresets’ sizes depend on a complexity measure called μy(X), but it remained unclear whether this dependence was inherent or an artifact of specific coreset methods. Existing coresets were also considered optimal without rigorous justification.
This work addresses these issues by establishing lower bounds on the space complexity needed to approximate logistic loss up to a relative error. They prove that for datasets with a constant μy(X) value, current coreset constructions are indeed near-optimal. Furthermore, they disprove previous conjectures by showing that μy(X) can be computed efficiently via linear programming. Finally, they analyze the use of low-rank approximations to achieve additive error guarantees in estimating the logistic loss. Overall, their findings provide valuable insights into the fundamental limits of approximating logistic loss and guide the design of future space-efficient algorithms.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in machine learning and data analysis. It provides tight lower bounds on the space complexity of approximating logistic loss, a fundamental problem in these fields. This directly impacts the design of efficient algorithms, particularly coresets, and guides future research on optimization techniques. The paper also offers an efficient algorithm for calculating a key complexity measure, furthering practical applications.
Visual Insights#
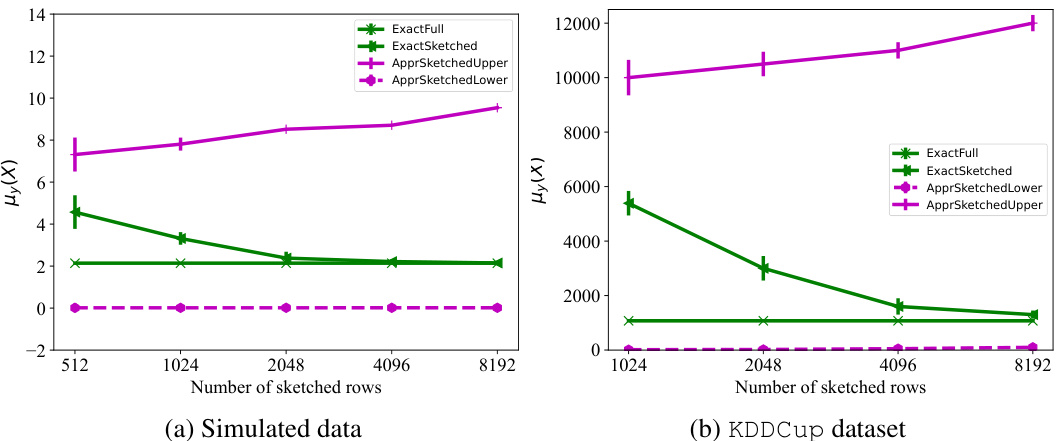
This figure compares the exact computation of the classification complexity measure μy(X) using the full dataset and sketched datasets of varying sizes against the approximate upper and lower bounds provided by Munteanu et al. [10]. The results demonstrate that the exact computation on sketched datasets closely matches the actual μy(X) of the full dataset, while the approximate bounds can be significantly loose.
Full paper#