↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Fine-tuning large pre-trained models often leads to a decline in out-of-distribution (OOD) performance, hindering their reliability in real-world scenarios where data may differ from the training distribution. This is known as the ID-OOD trade-off, a significant challenge addressed by ensemble methods. However, existing ensemble methods still suffer from this trade-off, exhibiting peak performance at different mixing coefficients for ID and OOD accuracy.
The paper introduces Variance Reduction Fine-tuning (VRF), a novel sample-wise ensembling technique. VRF leverages a Zero-Shot Failure (ZSF) set to create a sample-wise weighting scheme for ensemble predictions. This weighting is based on the distance of a test sample to the ZSF set. VRF effectively reduces variance in ensemble predictions, thereby minimizing residual errors. Experiments on various datasets demonstrate that VRF surpasses existing methods, achieving significant improvements in OOD accuracy while maintaining or even improving ID accuracy.
Key Takeaways#
Why does it matter?#
This paper is important because it tackles a critical issue in the field of machine learning: the ID-OOD trade-off during fine-tuning. By introducing the Variance Reduction Fine-tuning (VRF) method, it offers a solution to improve both in-distribution and out-of-distribution accuracy simultaneously. This is highly relevant to current research focusing on model robustness and generalization, opening new avenues for research into sample-wise ensembling techniques and improving model reliability in real-world applications.
Visual Insights#
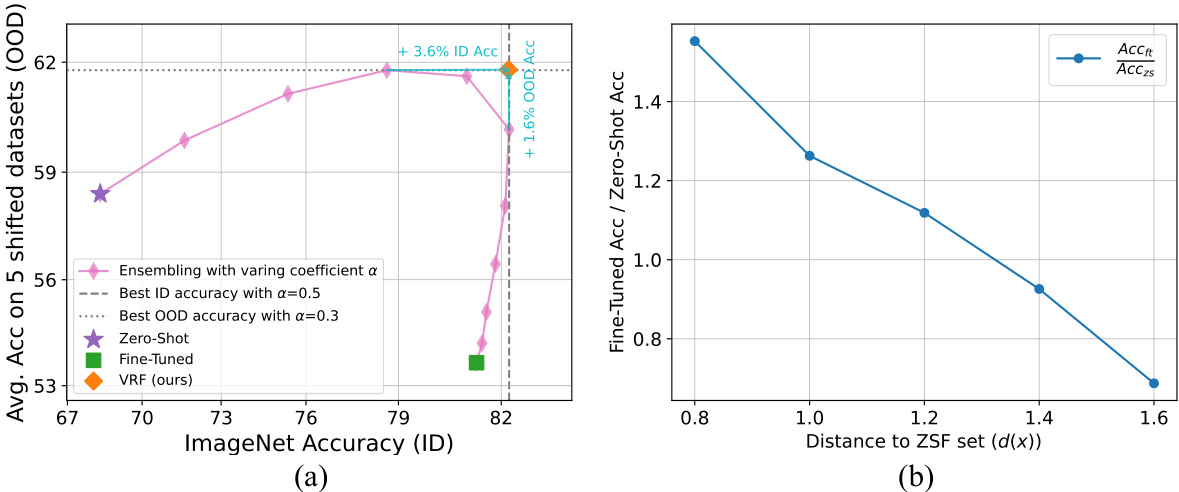
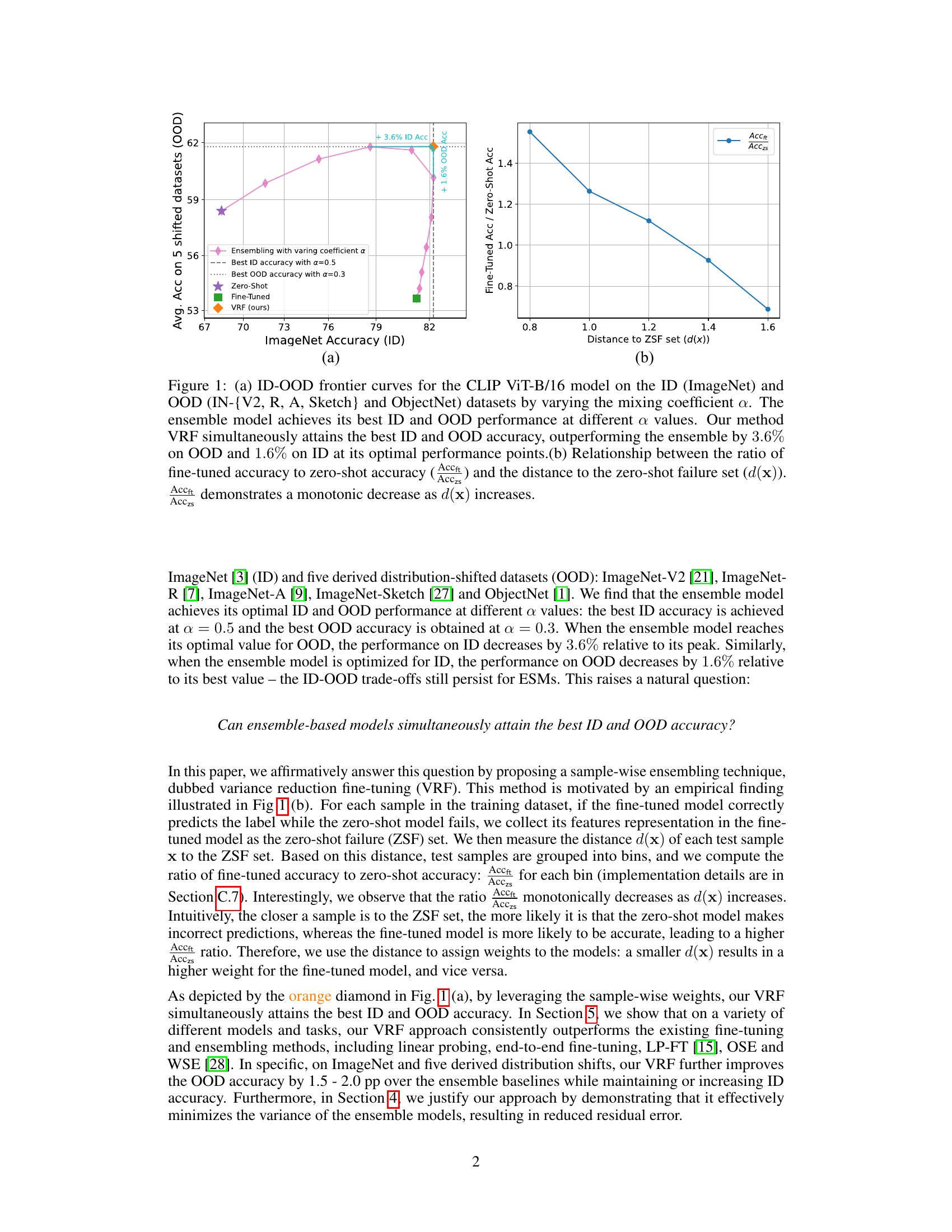
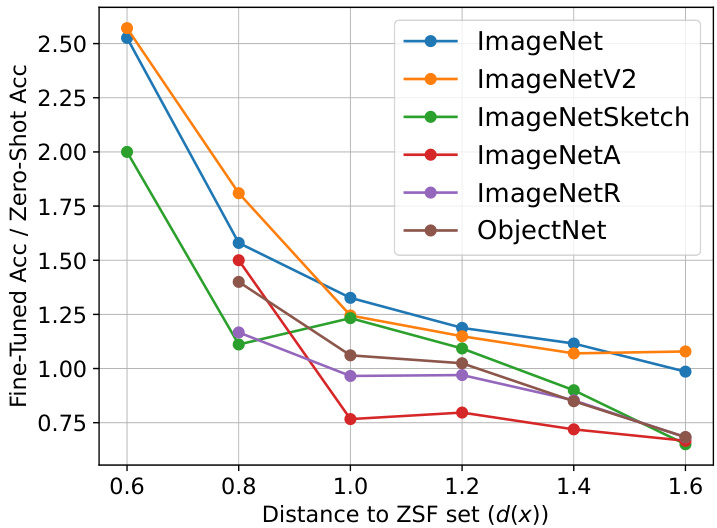
This figure shows the ID-OOD trade-off of ensemble methods and the proposed variance reduction fine-tuning (VRF) method. Subfigure (a) presents the ID-OOD frontier curves for the CLIP ViT-B/16 model. It shows that the ensemble model achieves the best ID and OOD accuracy at different mixing coefficients α, while VRF attains the best of both without trade-offs. Subfigure (b) shows the relationship between the ratio of fine-tuned accuracy to zero-shot accuracy and the distance to the zero-shot failure set, demonstrating a monotonic decrease in the ratio as the distance increases. This finding justifies the proposed VRF method.

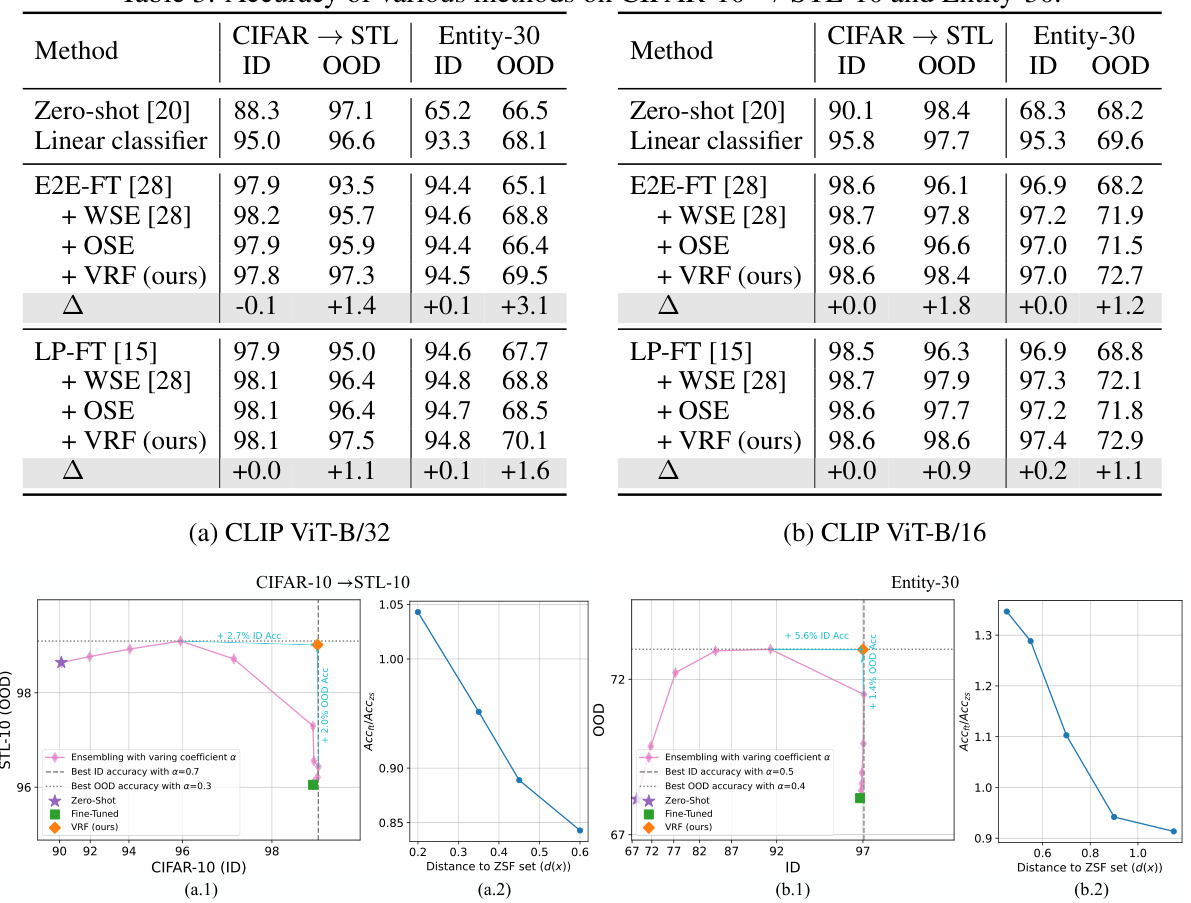
This table presents the accuracy of different methods (Zero-shot, Linear classifier, E2E-FT, Weight-space ensemble, Output-space ensemble, and VRF) on ImageNet and five derived distribution shifts (IN-V2, IN-Sketch, IN-A, IN-R, ObjectNet). It shows the average accuracy across all six datasets, highlighting the improvement achieved by the proposed Variance Reduction Fine-tuning (VRF) method compared to the baselines and other ensemble methods.
In-depth insights#
ID-OOD Tradeoffs#
The concept of ‘ID-OOD tradeoffs’ highlights a crucial challenge in machine learning: improving a model’s performance on in-distribution (ID) data often comes at the cost of its performance on out-of-distribution (OOD) data, and vice versa. This tradeoff is particularly pronounced in fine-tuning pre-trained models like CLIP, where enhancing ID accuracy can significantly reduce the model’s robustness to OOD data. Ensemble methods, while offering improved robustness, don’t fully resolve this issue, as they often exhibit peak performance for ID and OOD accuracy at different mixing coefficients. This necessitates a more nuanced approach to fine-tuning that can simultaneously optimize for both ID and OOD performance, avoiding the inherent trade-off. Strategies addressing this need focus on sample-wise ensembling, weighting model predictions based on their proximity to a set of training samples where the zero-shot model failed, thus reducing prediction variance and improving overall model robustness.
VRF Fine-tuning#
The proposed Variance Reduction Fine-tuning (VRF) method presents a novel approach to enhance the robustness of zero-shot models. VRF directly addresses the ID-OOD trade-off, a common challenge in fine-tuning where improvements in in-distribution (ID) accuracy often come at the cost of reduced out-of-distribution (OOD) performance. Unlike ensemble methods that struggle to optimize for both ID and OOD simultaneously, VRF uses a sample-wise ensembling strategy. It identifies a Zero-Shot Failure (ZSF) set, comprised of training samples misclassified by the zero-shot model but correctly classified by the fine-tuned model. The core idea is to weight the fine-tuned model’s prediction more heavily for test samples closer to the ZSF set, thus reducing variance and residual error in the ensemble. This approach demonstrably improves both ID and OOD accuracy across various datasets and model architectures, offering a significant advance in robust fine-tuning techniques. The effectiveness is further justified by demonstrating that VRF minimizes the variance of the ensemble model.
Variance Reduction#
The concept of ‘Variance Reduction’ in the context of fine-tuning zero-shot models centers on improving the reliability and generalization of these models by minimizing the variability in their predictions. High variance, often resulting from the inherent uncertainty in zero-shot settings and the sensitivity of fine-tuning to specific training data, leads to inconsistent performance across different inputs. By reducing this variance, the method aims to improve the robustness and accuracy of the model, especially in out-of-distribution (OOD) scenarios. The proposed variance reduction technique employs a sample-wise ensembling approach, dynamically weighting the contributions of zero-shot and fine-tuned models based on the proximity of test samples to a set of ‘zero-shot failures.’ This adaptive weighting mechanism effectively reduces the variance, leading to more consistent and reliable predictions. The key benefit lies in its ability to achieve optimal performance across in-distribution and OOD datasets, resolving the common ID-OOD trade-off problem. This approach differs from existing ensemble methods which use a fixed coefficient, highlighting the novelty and efficacy of a sample-wise approach for effective variance reduction.
ZSF Set Impact#
The effectiveness of the Variance Reduction Fine-tuning (VRF) method hinges significantly on the quality and composition of the Zero-Shot Failure (ZSF) set. A well-constructed ZSF set, comprised of samples where the zero-shot model fails but the fine-tuned model succeeds, provides crucial information for guiding the sample-wise ensembling process. The distance of a test sample to this ZSF set becomes a key determinant of its assigned weight, influencing the final prediction. A poorly constructed ZSF set, either due to inadequate identification of true failures or inclusion of irrelevant samples, could lead to inaccurate weight assignments and diminished performance of the VRF. Therefore, a robust method for creating the ZSF set, possibly involving careful selection criteria and/or handling of noisy labels, is paramount to maximizing the benefits of the VRF method. Further investigation is needed to understand the optimal size and composition of the ZSF set, as well as the sensitivity of the method to variations in its characteristics. The impact of the ZSF set is a vital area for further research to fully understand VRF’s robustness and reliability.
Future Directions#
Future research could explore several promising avenues. Extending VRF to other zero-shot models beyond CLIP is crucial to establish its generalizability. Investigating the impact of different distance metrics and dimensionality reduction techniques on VRF’s performance is important. Developing a more theoretically grounded understanding of why VRF works is needed, potentially by examining the relationship between variance reduction and generalization. Exploring the effectiveness of VRF in more complex scenarios, such as those with significant label noise or domain shifts, would enhance its practical applicability. Combining VRF with other robustness techniques could further improve performance. Finally, investigating the scalability and computational efficiency of VRF for very large datasets is vital for real-world applications.
More visual insights#
More on figures

The figure shows two subfigures. Subfigure (a) shows the ID-OOD trade-off curves for the CLIP ViT-B/16 model using different mixing coefficients. The ensemble model peaks at different mixing coefficients for in-distribution (ID) and out-of-distribution (OOD) accuracy, demonstrating the ID-OOD trade-off. The proposed Variance Reduction Fine-tuning (VRF) method, however, simultaneously achieves the best ID and OOD accuracies. Subfigure (b) illustrates the relationship between the ratio of fine-tuned to zero-shot accuracy and the distance to the Zero-Shot Failure (ZSF) set for each test sample. It shows that as the distance to the ZSF set increases, this accuracy ratio decreases monotonically.
This figure shows the ID-OOD trade-off for the CLIP ViT-B/16 model. The left subplot (a) displays the ID-OOD frontier curves, illustrating how ensemble methods (OSE and WSE) achieve peak ID and OOD accuracy at different mixing coefficients (α). In contrast, the proposed VRF method simultaneously achieves the best ID and OOD performance. The right subplot (b) shows the relationship between the ratio of fine-tuned accuracy to zero-shot accuracy and the distance of a test sample to the zero-shot failure (ZSF) set. This relationship demonstrates that the proposed method is effective in variance reduction.

This figure compares the performance of using only the zero-shot failure (ZSF) set versus using the entire fine-tuned (FT) training data set to compute the distance d(x) for each test sample x. The y-axis shows the ratio of fine-tuned accuracy to zero-shot accuracy (Accft/Acczs) and the x-axis shows the distance d(x). The plot demonstrates that using the ZSF set leads to a clearer monotonic decreasing trend, which is essential for the proposed Variance Reduction Fine-tuning (VRF) method. Using the entire FT dataset results in a less informative and non-monotonic trend, hindering the performance of VRF. The inset table shows the overall ID and OOD accuracies for both methods.

This figure presents the results of experiments evaluating the variance reduction fine-tuning (VRF) method. (a) shows the average weight assigned to the fine-tuned model across different datasets (ImageNet, CIFAR, and Entity30). (b) demonstrates the performance of VRF using logit-space ensembling, showing improved ID and OOD accuracy compared to baselines. (c) investigates the influence of the k-NN distance parameter on the results. The consistent increase in OOD accuracy suggests VRF’s effectiveness.
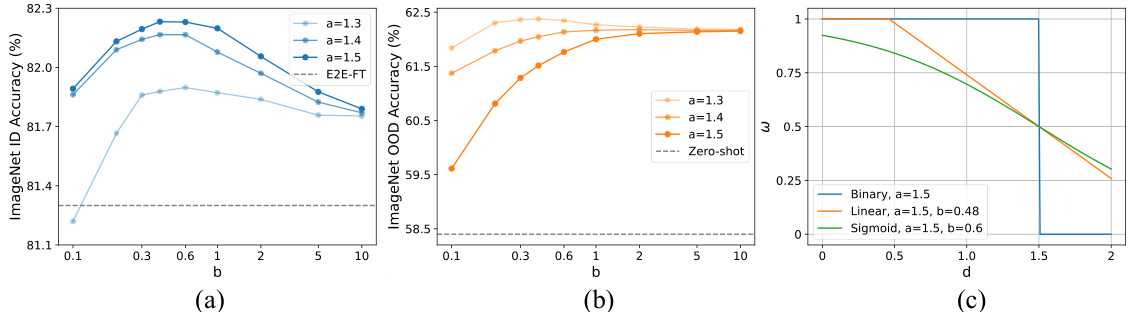
This figure analyzes the impact of hyperparameters a and b on the performance of the proposed Variance Reduction Fine-tuning (VRF) method. Subfigure (a) shows how different combinations of a and b affect ImageNet in-distribution (ID) accuracy. Subfigure (b) similarly displays their effect on out-of-distribution (OOD) accuracy. Finally, subfigure (c) compares the performance of the VRF method using different weight functions (binary, linear, and sigmoid) to demonstrate the effectiveness of the sigmoid function selected for VRF in the paper.

This figure visualizes examples of images with the smallest and largest distances to the Zero-Shot Failure (ZSF) set. The images with the smallest distances are predominantly fine-grained species, where the fine-tuned models have more specific knowledge not present in the zero-shot models. Conversely, images with the largest distances show styles (tattoos, cartoons, sketches) different from the fine-tuning samples; styles where zero-shot models tend to perform better.
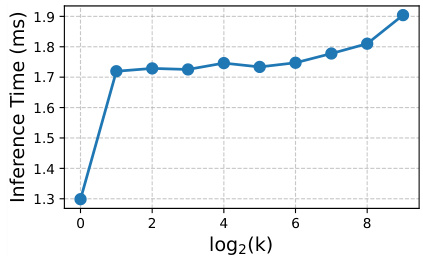
This figure shows the inference speed (in milliseconds per image) for computing the k-nearest neighbor distance using different values of k. The x-axis represents log2(k), and the y-axis shows the inference time. As k increases, the inference time also increases, but the increase is relatively slow, especially for smaller values of k. This indicates that the k-NN search can be efficiently implemented, even for relatively large values of k.

This figure shows the ID-OOD trade-off for the CLIP ViT-B/16 model using different mixing coefficients (a) in ensemble methods and the proposed VRF method. Subfigure (a) demonstrates that the ensemble methods achieve peak ID and OOD accuracy at different mixing coefficients, revealing the ID-OOD trade-off. Subfigure (b) shows a monotonic relationship between the ratio of fine-tuned accuracy to zero-shot accuracy (Accft/Acczs) and the distance to the zero-shot failure set (d(x)), a key observation motivating the VRF approach.
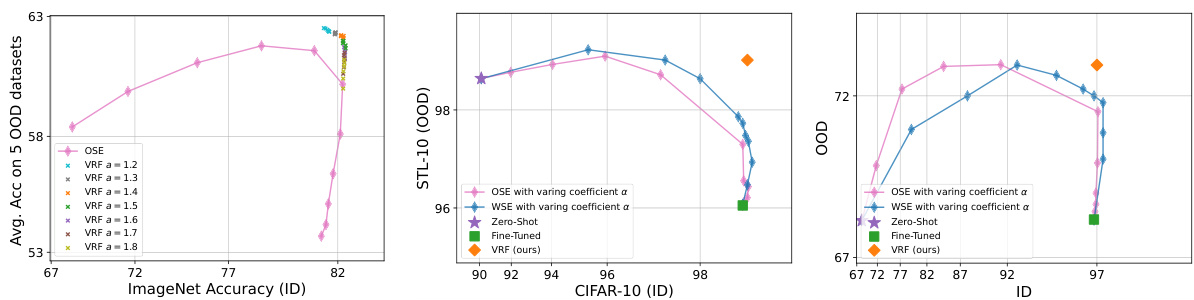
This figure shows the ID-OOD trade-off curve for the CLIP ViT-B/16 model with varying mixing coefficients (α). It demonstrates that ensemble methods achieve peak performance for ID and OOD accuracy at different mixing coefficients. The proposed Variance Reduction Fine-tuning (VRF) method, however, achieves the best ID and OOD accuracy simultaneously. The second subplot shows the relationship between the ratio of fine-tuned to zero-shot accuracy and the distance to a set of training samples that were incorrectly predicted by the zero-shot model (ZSF set). This illustrates the core concept behind VRF, which is to weight the fine-tuned model more strongly for test samples close to this ZSF set.
This figure shows two plots. Plot (a) presents the ID-OOD trade-off curves for the CLIP ViT-B/16 model when using different mixing coefficients (α) in the output-space ensemble method. It highlights that optimal ID and OOD accuracies occur at different α values, demonstrating the ID-OOD trade-off. The authors’ proposed method (VRF) achieves superior performance in both ID and OOD, exceeding the ensemble’s performance. Plot (b) illustrates the relationship between the ratio of fine-tuned accuracy to zero-shot accuracy and the distance to the Zero-Shot Failure (ZSF) set. It shows an inverse relationship, supporting the authors’ use of this distance in their VRF method to assign weights in the ensemble.
More on tables
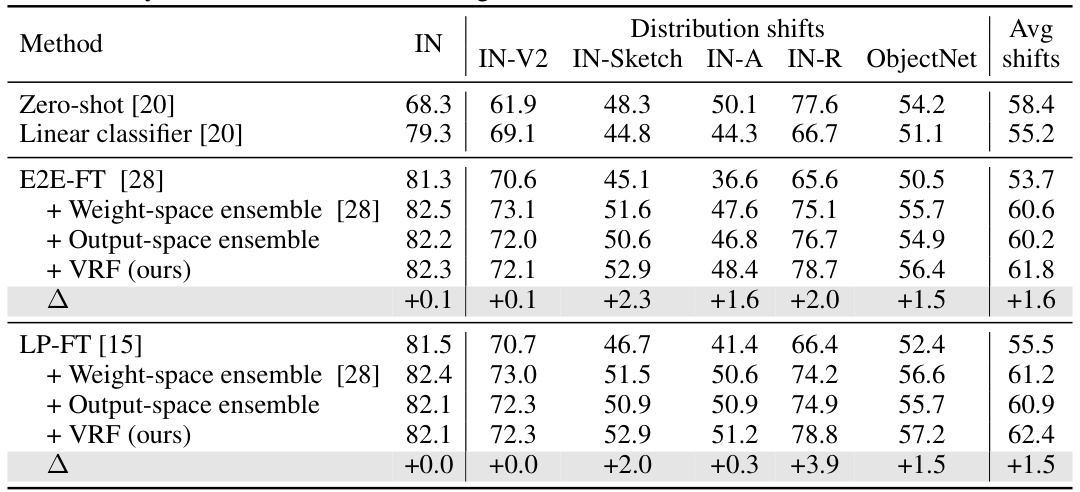
This table presents the accuracy of various methods (Zero-shot, Linear classifier, E2E-FT, Weight-space ensemble, Output-space ensemble, and VRF) on ImageNet and five derived distribution shifts (IN-V2, IN-Sketch, IN-A, IN-R, ObjectNet). It compares the performance of these methods across different distribution shifts and highlights the improvement achieved by the proposed VRF method over existing ensemble methods.
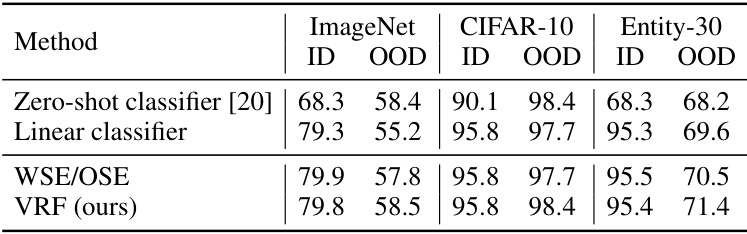
This table presents the results of applying the Variance Reduction Fine-tuning (VRF) method to linear-probed models using the CLIP ViT-B/16 architecture. It compares the performance of VRF against several baselines including the zero-shot classifier, a linear classifier, and the Weight-space/Output-space ensemble (WSE/OSE) methods. The results are shown for the ImageNet, CIFAR-10, and Entity-30 datasets, reporting the ID (In-distribution) and OOD (Out-of-distribution) accuracies for each method.
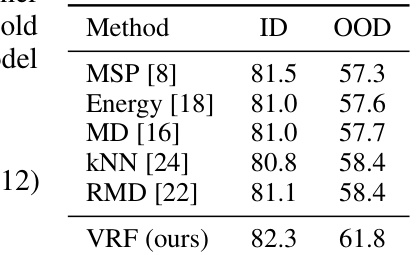
This table compares the performance of several OOD detection methods with the proposed VRF method on ImageNet. The ID and OOD accuracies are presented, demonstrating that VRF outperforms existing techniques for handling out-of-distribution data.

This table presents the ImageNet ID and OOD accuracy results for three different designs of the weight function ω in the VRF method: Binary, Linear, and Sigmoid. The results show a comparison of the performance of these different weight functions on the ImageNet dataset, demonstrating the effectiveness of the Sigmoid function compared to simpler alternatives.
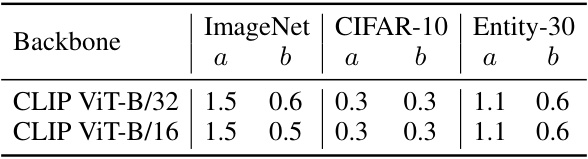
This table shows the optimal hyperparameters 'a' and 'b' for the VRF method, on different datasets and backbones. The hyperparameters were determined through a search process on the validation set, using the ID accuracy to guide the selection. The values were then used for evaluation across a variety of datasets. The table provides a concise summary of the optimal settings for the VRF model’s performance across different experimental settings.
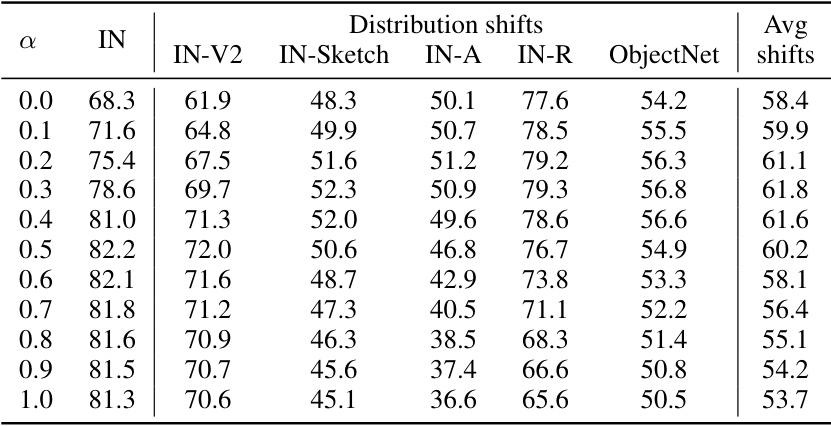
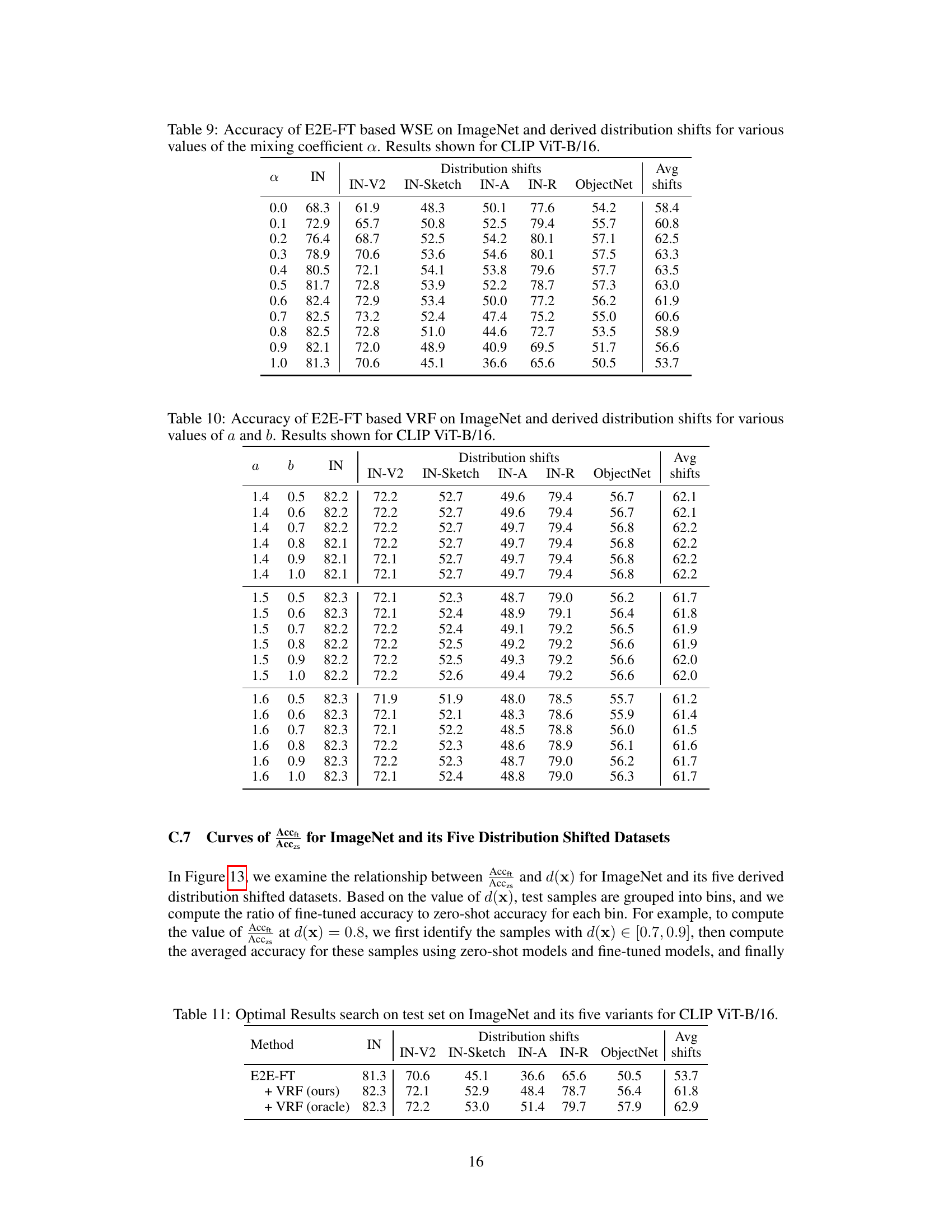
This table presents the accuracy of the output-space ensemble (OSE) method, combined with end-to-end fine-tuning (E2E-FT), on ImageNet and five of its distribution shift variations. The results are shown for the CLIP ViT-B/16 model, and the accuracy is shown for different values of the mixing coefficient α, which controls the weighting between the zero-shot model and the fine-tuned model within the ensemble. The table demonstrates how the accuracy varies across the different datasets for varying mixing coefficients.

This table presents the accuracy of the output-space ensemble (OSE) method applied to the end-to-end fine-tuned (E2E-FT) model for CLIP ViT-B/16 on ImageNet and its five derived distribution shifts. The accuracy is shown for different values of the mixing coefficient (α), ranging from 0.0 to 1.0. Each row represents a different α value, and the columns display the accuracy for ImageNet (IN), and the five distribution shifts: ImageNet-V2 (IN-V2), ImageNet-Sketch (IN-Sketch), ImageNet-A (IN-A), ImageNet-R (IN-R), and ObjectNet. The final column shows the average accuracy across all six datasets for each α value.
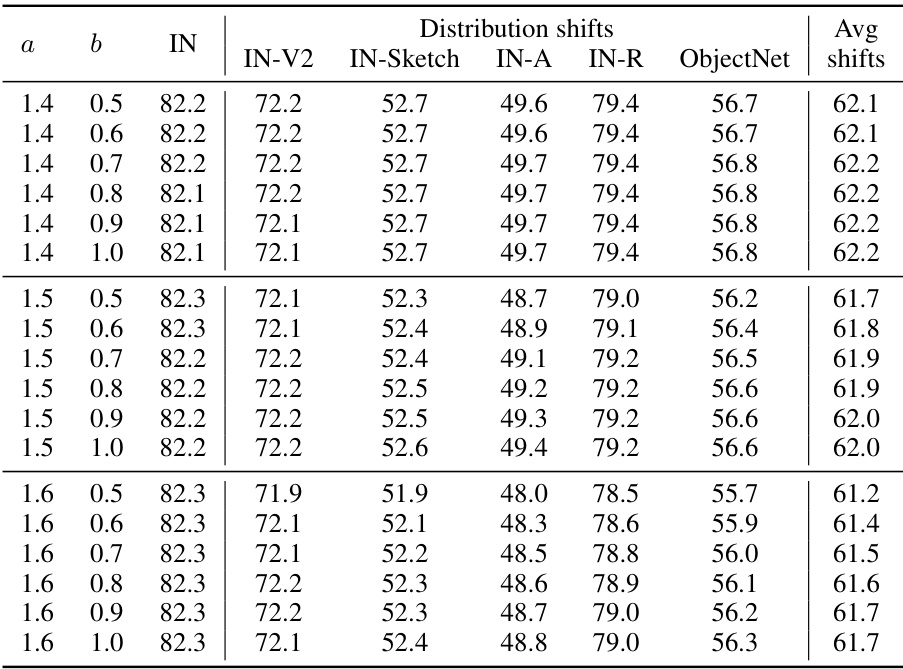
This table presents the accuracy of the end-to-end fine-tuned (E2E-FT) model with variance reduction fine-tuning (VRF) applied on the ImageNet dataset and its five derived distribution shifts. The results are shown for the CLIP ViT-B/16 model. The table shows how the accuracy varies with different values of hyperparameters ‘a’ and ‘b’ in the VRF method. ‘a’ and ‘b’ are used in the sigmoid function to determine the weight assigned to the fine-tuned model in the ensemble.
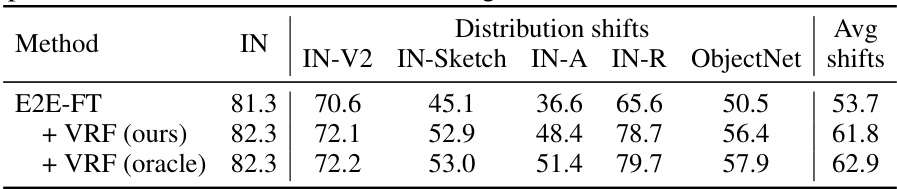
This table presents the optimal results obtained by searching the hyperparameters on test sets for ImageNet and its five variants using the CLIP ViT-B/16 model. It compares the accuracy of the E2E-FT method with and without VRF, and also includes an oracle VRF result for comparison. The table highlights the improvements achieved in ID and OOD accuracy by VRF.
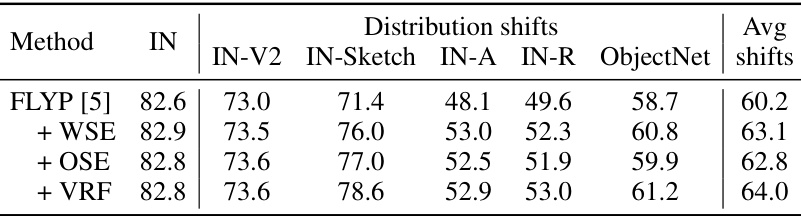
This table presents the results of applying the Variance Reduction Fine-tuning (VRF) method to other robust fine-tuning methods, namely FLYP, Weight-space ensemble (WSE), and Output-space ensemble (OSE). The performance is evaluated on ImageNet and five derived distribution shifts (IN-V2, IN-Sketch, IN-A, IN-R, ObjectNet). The table shows the average accuracy across these six datasets, demonstrating the improvement achieved by incorporating VRF into these existing methods. Specifically, it shows that VRF consistently enhances the robustness of the models across various distribution shifts while maintaining similar ID accuracy.

This table compares the performance of various OOD detectors (MSP, Energy, MD, kNN, RMD) with the proposed VRF method on the ImageNet dataset and its five derived distribution shifts. The results show the ID accuracy (ImageNet), OOD accuracy across five distribution shifts, and the average OOD accuracy. It highlights the ability of VRF to outperform traditional OOD detectors in terms of OOD accuracy while maintaining a competitive ID accuracy.
Full paper#