↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Self-supervised learning (SSL) and contrastive learning methods, such as those used in CLIP and DINO, often employ various forms of data balancing. However, the precise impact of these balancing techniques on model training and performance has remained unclear. The effectiveness of such methods is often attributed to factors like preventing model collapse or improving representation quality, but these explanations are limited. This paper tackles this knowledge gap by demonstrating that data balancing offers an unexpected yet significant advantage: variance reduction.
The authors introduce a new theoretical framework that provides a non-asymptotic statistical bound quantifying the variance reduction effect due to data balancing. This bound connects the variance reduction to the eigenvalue decay of Markov operators that are constructed from the conditional means given X and Y. By employing this framework, they demonstrate how various forms of data balancing in contrastive multimodal learning and self-supervised clustering can be better understood, and potentially improved upon, through the lens of variance reduction.
Key Takeaways#
Why does it matter?#
This paper is crucial because it reveals an unexpected benefit of data balancing in foundation models: variance reduction. This finding enhances our understanding of self-supervised learning and opens avenues for improving model training and performance. The theoretical framework provided offers a new perspective for researchers working with multimodal data and contrastive learning methods, paving the way for improved model efficiency and effectiveness.
Visual Insights#
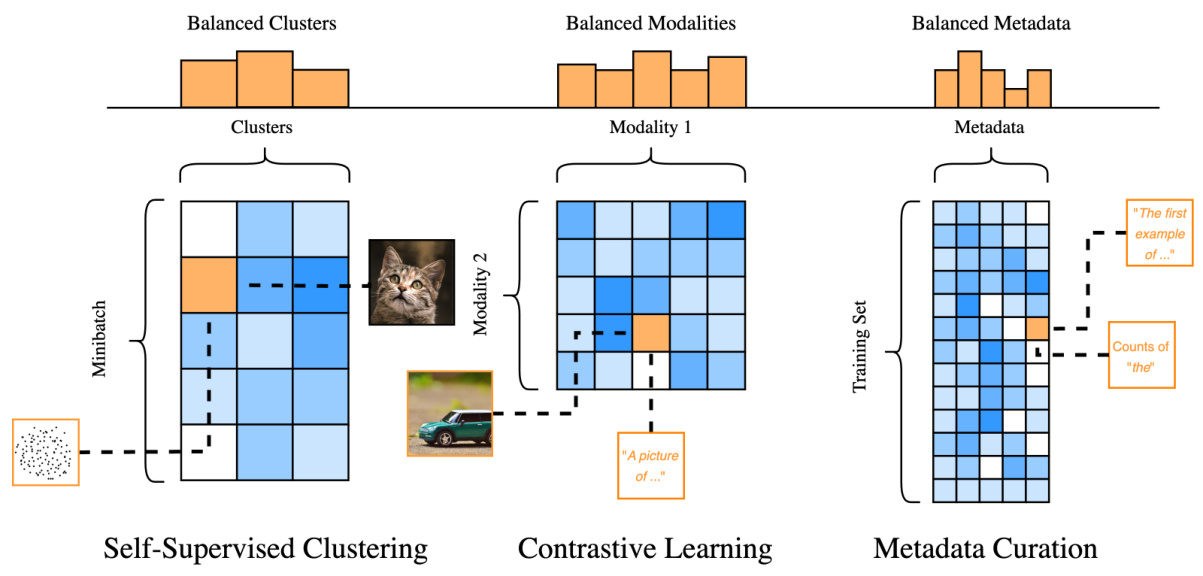
This figure illustrates three different applications of data balancing. The left panel shows self-supervised clustering, where data points (images) are mapped to features (X) and pseudo-labels (Y, representing cluster assignments). The center panel depicts contrastive learning, mapping image-text pairs to image features (X) and text features (Y). The right panel demonstrates metadata curation, mapping text data to text features (X) and keyword matches (Y). In each case, data balancing aims to adjust the probability distribution over features and labels to match the target marginals (represented by the orange histograms), improving the model’s performance.

This table lists the symbols used throughout the paper, their descriptions, and the page number where they are defined. It includes notation for sample spaces, probability measures, estimators, operators, and function spaces relevant to the paper’s mathematical analysis.
In-depth insights#
Data Balancing’s Impact#
Data balancing, while seemingly a simple preprocessing step, has a profound impact on the performance and generalization ability of machine learning models, particularly deep learning models. The core impact of data balancing is variance reduction. By ensuring a more uniform distribution of data across different classes or modalities, data balancing reduces the influence of highly prevalent classes or features, leading to more stable and robust model training. This is especially crucial in contrastive learning or self-supervised learning settings where data augmentation and pseudo-label generation may introduce biases that favor certain features. The resulting models are less susceptible to overfitting to specific data characteristics and demonstrate improved performance on unseen data. While data balancing techniques are shown to enhance model performance, it is crucial to understand that the choice of balancing method (e.g., undersampling, oversampling, data augmentation), balancing parameters, and the nature of the underlying data distribution significantly influence the outcomes. Careful consideration of these factors is critical for effective data balancing. Simply using data balancing does not always guarantee improved performance, and even may have negative side effects in certain settings. Thus, a thoughtful approach to balancing strategy is more important than simply applying any balancing technique. The ultimate impact of data balancing hinges on a thorough understanding of the data and the model’s learning process.
Variance Reduction#
The concept of variance reduction is central to the research paper, demonstrating how data balancing techniques, often employed in foundation models for seemingly unrelated reasons, actually contribute to reducing the variance of empirical estimators. The authors establish a non-asymptotic statistical bound quantifying this variance reduction effect, linking it to the eigenvalue decay of Markov operators. This unexpected benefit of data balancing techniques is a key finding, offering a novel theoretical perspective on established practices. The analysis uncovers a connection between nonlinear balancing iterations and linear operators on vector spaces. By leveraging singular value decompositions, the variance reduction is precisely quantified and linked to the spectral properties of conditional mean operators. This provides a powerful analytical tool for understanding and potentially improving upon various data balancing techniques. The authors further illustrate the practical applications and implications of this theoretical framework through numerical illustrations on real-world examples including CLIP-type objectives and metadata curation. Their analysis provides a new theoretical lens for understanding and improving self-supervised learning, highlighting the underappreciated role of variance reduction in these advanced models. The mathematical rigor and clarity combine with concrete examples to provide a significant contribution to the field.
CLIP’s Implicit Balance#
The heading “CLIP’s Implicit Balance” suggests an insightful analysis of Contrastive Language-Image Pre-training (CLIP). CLIP, while seemingly optimizing a straightforward objective, implicitly incorporates data balancing. The authors likely demonstrate that the model’s success stems from a balancing act between image and text modalities. This means that CLIP’s training process doesn’t just minimize a loss function but also subtly adjusts the distribution of image-text pairs to achieve a better representation of both modalities. The analysis might reveal a previously unknown connection between CLIP’s training dynamics and the principles of variance reduction in machine learning, suggesting that data balancing acts as an implicit regularizer, improving the model’s generalization and robustness. This could explain the surprising effectiveness of CLIP’s training recipe and offer valuable insights for designing future multimodal learning models. The section likely presents theoretical analysis supporting these claims, possibly involving statistical bounds and the spectral properties of Markov operators. Understanding this “implicit balance” could lead to improvements on CLIP’s architecture and training methodologies, potentially leading to more efficient and effective multimodal models.
Theoretical Guarantees#
A section on ‘Theoretical Guarantees’ in a research paper would rigorously establish the accuracy and reliability of the proposed methods. It would likely present mathematical bounds or convergence rates, demonstrating how the algorithm’s performance scales with key factors like the size of the dataset, dimensionality of the data, or the number of iterations. The guarantees might quantify the probability of error, providing confidence intervals or worst-case scenarios for the results. Crucially, a strong theoretical analysis would clarify the assumptions underlying the guarantees, thus defining the context in which the theoretical results hold. Proofs of these guarantees, often mathematically complex, would be a core component, ensuring the validity of claims. Ultimately, this section aims to build trust in the method by proving its efficacy under specified conditions, transcending empirical results alone.
Future Research#
Future research directions stemming from this work on data balancing in foundation models could explore several promising avenues. Extending the theoretical analysis to more complex settings, such as those with continuous data spaces or more intricate dependence structures between modalities, would significantly enhance the practical applicability of the findings. Furthermore, investigating the impact of different balancing algorithms and their convergence rates under various conditions (e.g., noisy data, imbalanced datasets) would be crucial. Incorporating prior information about the data sources into the balancing process, potentially through Bayesian methods, could improve the accuracy and efficiency of the techniques. Finally, empirical evaluation on a broader range of foundation models and downstream tasks is necessary to validate the generalizability of the variance reduction effect observed in the study.
More visual insights#
More on figures
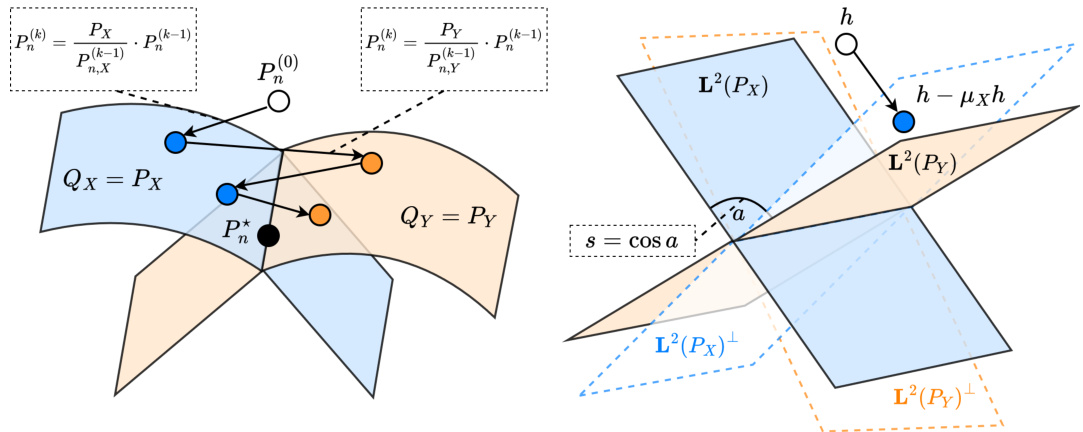
The figure visually represents the data balancing process. The left panel shows the nonlinear iterations in the space of probability measures, illustrating how the process alternates between projecting onto the set of distributions with X-marginal equal to Px (blue) and the set of distributions with Y-marginal equal to Py (orange). The right panel illustrates the corresponding linear operators (μx, μy) in the Hilbert space L²(P), showing their singular value decomposition and the relationship between the singular values and the angle between the subspaces L²(Px) and L²(Py). This visualization helps understand the variance reduction achieved through data balancing.
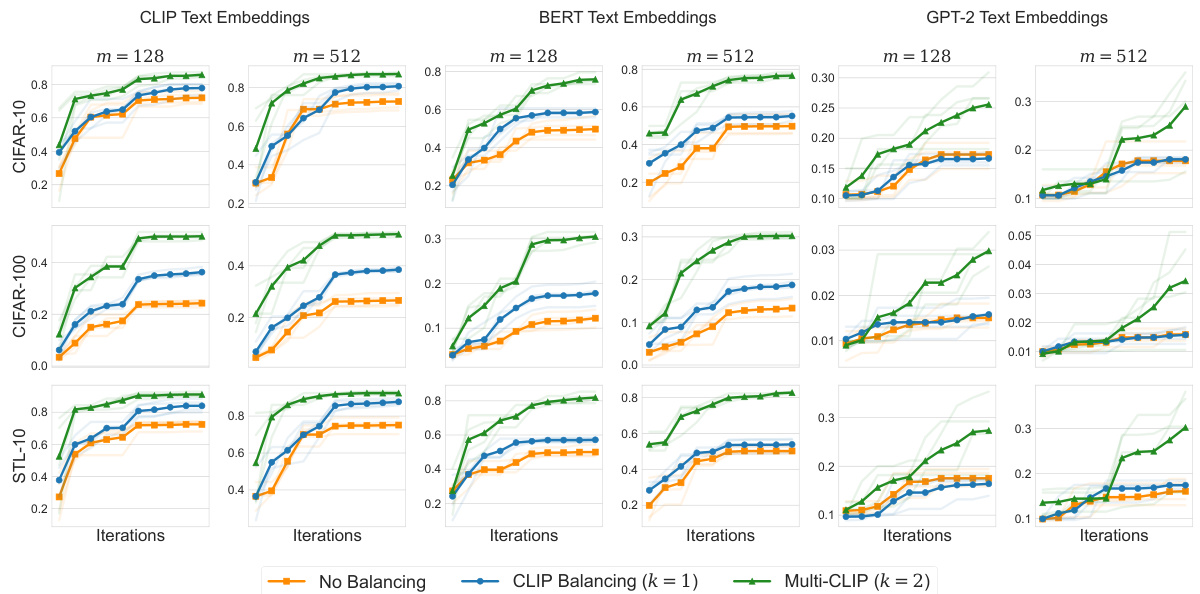
This figure shows the results of zero-shot image classification experiments using different text encoders (GPT-2, BERT, CLIP), batch sizes (128, 512), and datasets (CIFAR-10, CIFAR-100, STL-10). The plots show the average per-class recall (y-axis) as a function of training iterations (x-axis). It demonstrates how data balancing impacts zero-shot classification performance.
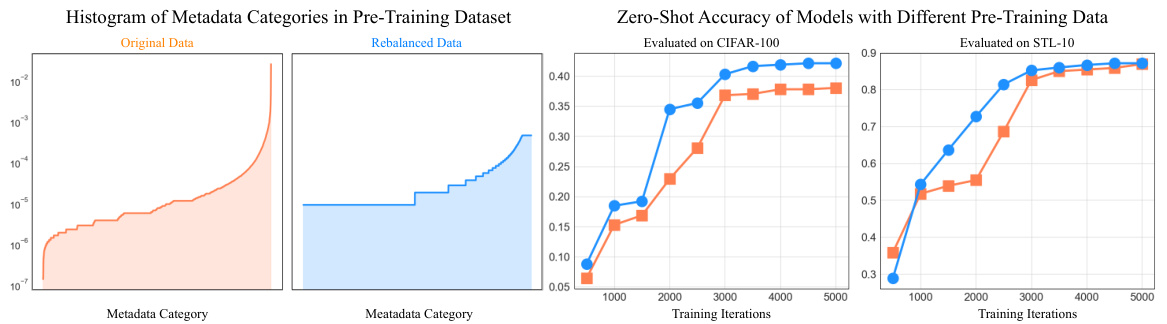
This figure shows the effect of data balancing on metadata curation for image caption pairs. The left panel displays the original and balanced distributions of keywords (metadata). The right panel demonstrates the zero-shot classification accuracy on CIFAR-100 and STL-10 datasets using models trained on both the original and balanced datasets. The results show that balancing leads to a more uniform keyword distribution and can improve the performance of the model.

This figure compares three methods for estimating a linear functional from data with misspecified marginal distributions. The methods are the empirical measure, an importance weighted estimator, and a data balancing estimator. The x-axis shows the dependence level between the two variables (higher values meaning more dependence). The y-axis shows the mean squared error. The different colored lines show the results with different levels of noise added to the marginal distributions provided to the estimators. The figure shows how the balancing estimator outperforms the other methods.
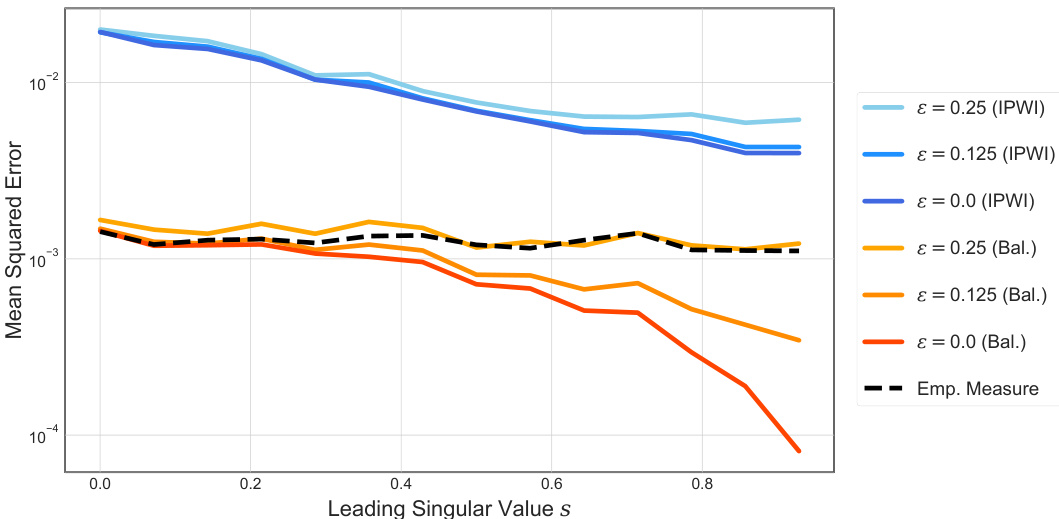
This figure compares three methods for estimating a linear functional of a probability distribution: the empirical measure, an importance weighted estimator, and the balanced estimator. It shows how the mean squared error (MSE) of these estimators varies with the dependence between two random variables (represented by the leading singular value ’s’) and the amount of noise in the provided marginal distributions (represented by ‘ε’). The results demonstrate that the balanced estimator generally outperforms the other two, especially when the variables are highly dependent.
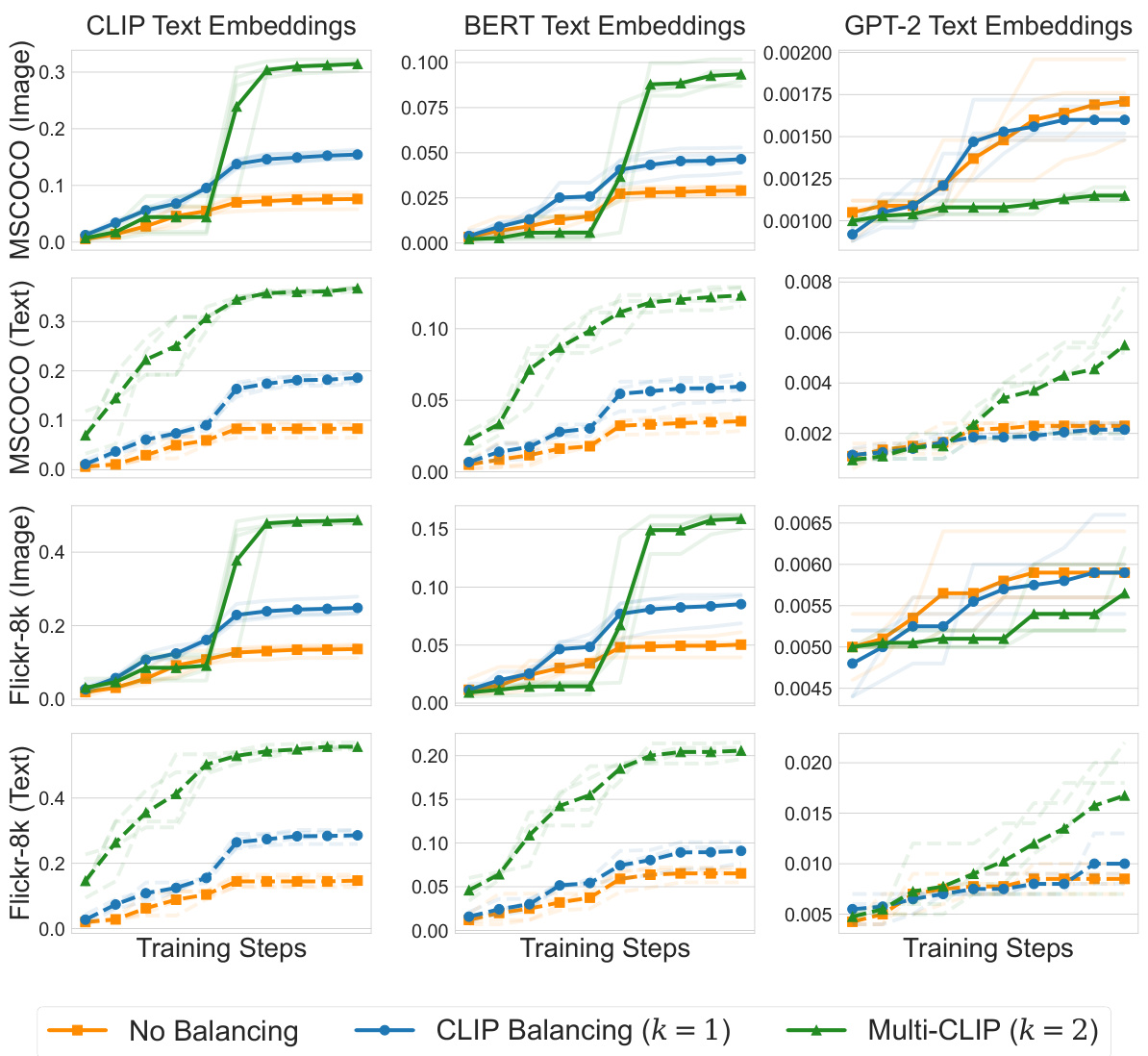
This figure shows the results of zero-shot retrieval experiments using different text encoders (GPT-2, BERT, CLIP) and data balancing techniques. The performance is measured by recall@5 for both image and text retrieval tasks across different datasets (MS-COCO and Flickr8k). The x-axis represents the number of training iterations, and the y-axis shows the recall@5 metric. Different colored lines represent different data balancing approaches (No Balancing, CLIP Balancing, Multi-CLIP).

This figure shows the performance of linear probing on three different datasets (Rendered SST2, VOC2007, and FGVC Aircraft). The results are shown for three different text encoders (GPT-2, BERT, and CLIP). The x-axis represents the number of training steps, and the y-axis represents the average per-class recall. It demonstrates how the quality of the text encoder and the number of balancing iterations affect the performance of the linear probing task.
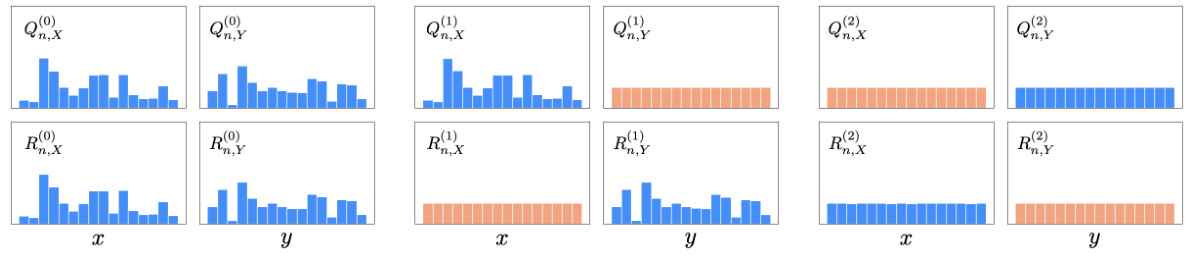
This figure shows the empirical marginal distributions obtained from the CLIP contrast matrix at different iterations of the balancing procedure. The left panel shows the initial distributions, which are not uniform. The middle panel shows the distributions after one iteration, which are closer to uniform. The right panel shows the distributions after two iterations, which are nearly uniform. This illustrates how the balancing procedure helps to reduce the variance of the empirical objective function.
Full paper#



















