↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Deep learning models struggle with noisy labels, leading to decreased accuracy. Existing solutions often use robust loss functions but face underfitting. This paper introduces e-softmax, a simple yet effective method to approximate one-hot vectors, improving model robustness.
E-softmax modifies the softmax layer outputs, implicitly changing the loss function. The paper proves that e-softmax ensures noise-tolerant learning with a controllable excess risk bound. By incorporating e-softmax with a symmetric loss function, it achieves a better balance between robustness and the ability to fit clean data, outperforming other methods in extensive experiments.
Key Takeaways#
Why does it matter?#
This paper is important because it offers a novel and effective solution to the persistent problem of noisy labels in training deep learning models. It provides a theoretical framework and practical methodology, thereby improving the robustness and accuracy of models in real-world applications where perfect data is scarce. The proposed e-softmax method is easily integrated into existing models, making it highly practical for researchers. This opens up new avenues for research into noise-tolerant learning and its applications.
Visual Insights#

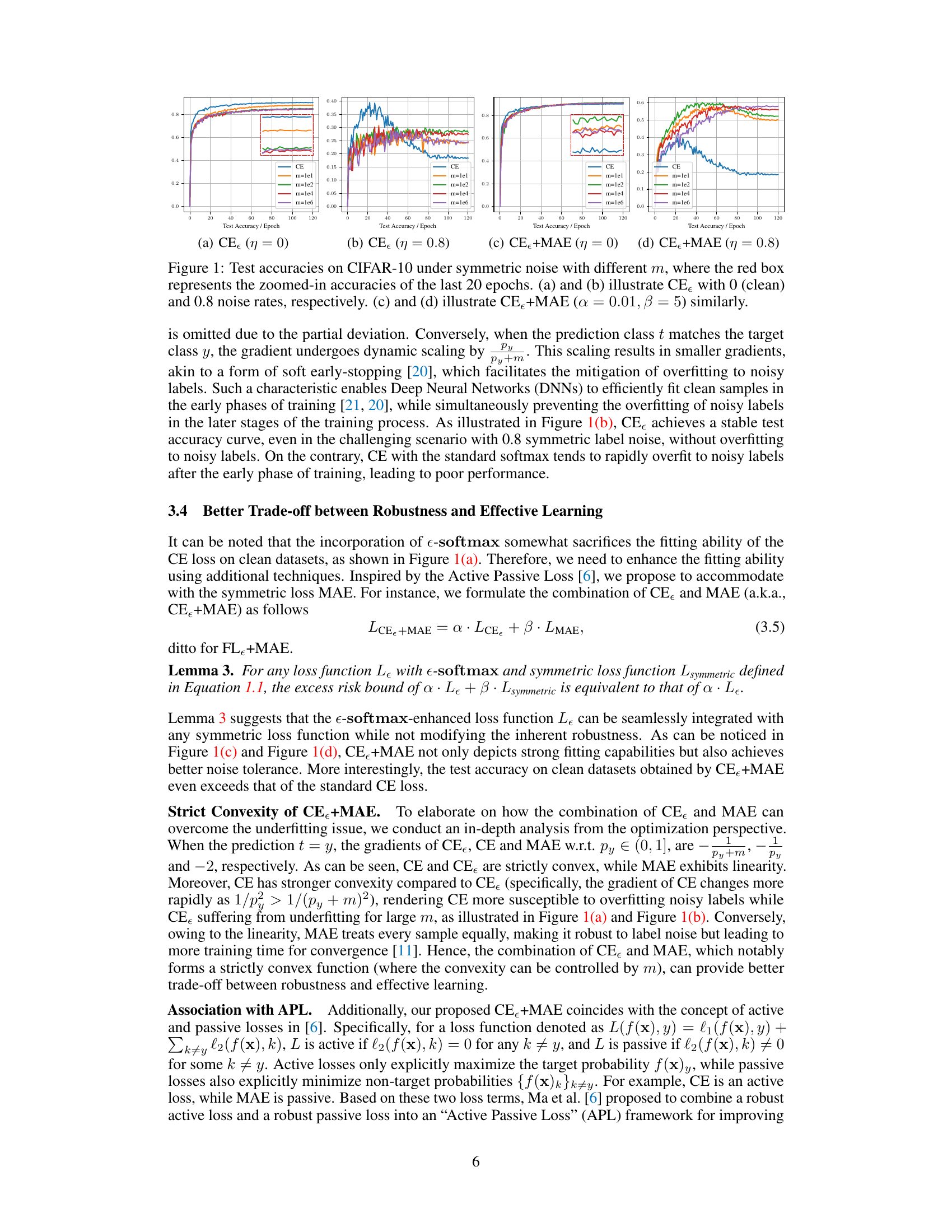
This figure compares the test accuracy of using cross-entropy loss (CE) and CE combined with mean absolute error (MAE) loss on the CIFAR-10 dataset under different symmetric noise rates. The parameter ’m’ in e-softmax is varied, showing its effect on model performance. The zoomed-in section highlights the performance in the later epochs of training. The results illustrate how the proposed methods (CE and CE+MAE) handle different noise levels and the impact of the ’m’ parameter on model robustness and accuracy.
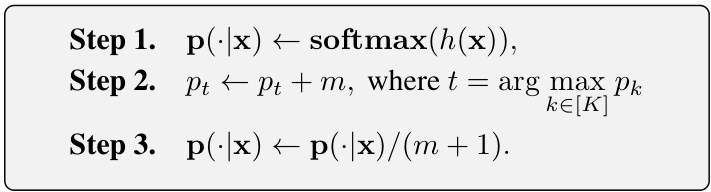
This table presents the test accuracy results for various methods (CE, FL, GCE, NLNL, SCE, NCE+MAE, NCE+RCE, NFL+RCE, NCE+AUL, NCE+AGCE, NCE+AEL, LDR-KL, CE+LC, CE+MAE, FLE+MAE) on CIFAR-10 and CIFAR-100 datasets under different symmetric and asymmetric noise rates (0, 0.1, 0.2, 0.3, 0.4, 0.6, 0.8). The results are averaged over three random runs, and the top two best results are highlighted in bold.
In-depth insights#
e-Softmax’s Robustness#
The e-softmax method’s robustness stems from its ability to approximate one-hot vectors, a crucial step in mitigating label noise. By directly manipulating the softmax layer outputs, e-softmax introduces a controllable error (ε) that relaxes the strict symmetry conditions often imposed by traditional robust loss functions. This relaxation prevents the underfitting frequently observed in symmetric loss functions like MAE, while still achieving noise tolerance. The controllable error parameter (m) allows for a trade-off between robustness and fitting ability. Theoretically, e-softmax guarantees a controllable excess risk bound, even under asymmetric noise, indicating its robustness and applicability to various loss functions. Empirically, e-softmax consistently demonstrates superior performance in the presence of both synthetic and real-world label noise, highlighting its effectiveness as a practical and theoretically sound method for enhancing robustness in deep learning.
Noise-Tolerant Learning#
Noise-tolerant learning tackles the challenge of training machine learning models effectively when dealing with noisy labels in datasets. The core issue is that inaccurate labels mislead the model, hindering its ability to generalize and predict accurately on unseen data. Approaches to address this involve modifying the learning process itself. Robust loss functions, such as those that down-weight the influence of outliers or that incorporate label uncertainty, are frequently employed. Another strategy is to use data augmentation or cleaning techniques to pre-process the data, filtering out obviously noisy samples or creating synthetic, ‘cleaner’ examples. Regularization methods can also be beneficial, helping prevent overfitting to noisy labels. Furthermore, some methods focus on semi-supervised learning, incorporating unlabeled data to improve robustness. Theoretical analysis of noise-tolerant methods often focuses on bounding excess risk, which reflects the difference in performance between models trained on noisy and clean data. The development of novel noise models also plays a key role, allowing for more realistic simulations and evaluation of techniques.
Theoretical Guarantees#
A robust theoretical foundation is crucial for any machine learning method, especially those designed to handle noisy data. Theoretical guarantees would ideally provide mathematical proof of a method’s effectiveness, demonstrating its ability to generalize well and perform reliably even when faced with imperfect information. In the context of label noise, such guarantees might establish bounds on the excess risk, proving that the algorithm’s performance under noisy labels remains close to its performance with clean labels. Strong theoretical guarantees are essential for building trust and confidence in the method’s reliability and are a key component in a comprehensive evaluation. They allow researchers to understand the limitations of the proposed method, understand which conditions are essential for its successful application, and anticipate its behavior under various circumstances. The absence of such guarantees might indicate that the method is purely empirical and may not generalize well to different datasets or noise conditions. In the presence of theoretical guarantees, one can expect a more robust and reliable model that is not only capable of achieving high accuracy but also provides confidence in its results.
Empirical Validation#
An empirical validation section in a research paper would rigorously test the proposed method’s effectiveness. This would involve carefully designed experiments on multiple datasets, including both standard benchmarks and real-world datasets with varying levels of noise. The results would be compared against other state-of-the-art methods to demonstrate the proposed method’s superiority. Quantitative metrics like accuracy, precision, recall, and F1-score would be reported, along with appropriate error bars or statistical significance testing to ensure the reliability of the findings. A thorough analysis of the results, including an exploration of the method’s behavior under different noise conditions, would provide valuable insights into its strengths and weaknesses. Ablation studies, systematically removing parts of the method, can isolate the contribution of specific components. Finally, the section would offer a clear and concise discussion of the results, relating the empirical findings back to the theoretical analysis and highlighting any unexpected or surprising observations. Visualization techniques, such as t-SNE plots to show learned representations or confusion matrices, could offer additional insights into the method’s performance. Overall, a well-executed empirical validation section is crucial for establishing the credibility and impact of the research.
Future Directions#
Future research could explore more sophisticated noise models that capture the complexities of real-world label noise, moving beyond simplistic symmetric or asymmetric assumptions. Investigating the interaction between e-softmax and different regularization techniques could reveal further improvements in robustness and generalization. The theoretical analysis could be extended to cover a wider range of loss functions and noise distributions, providing a more general framework for noise-tolerant learning. Practical applications in areas like medical image analysis and natural language processing, where noisy labels are prevalent, should be explored. Finally, research could focus on developing adaptive methods that automatically adjust the hyperparameter ε in e-softmax based on data characteristics, optimizing the trade-off between robustness and effective learning.
More visual insights#
More on figures

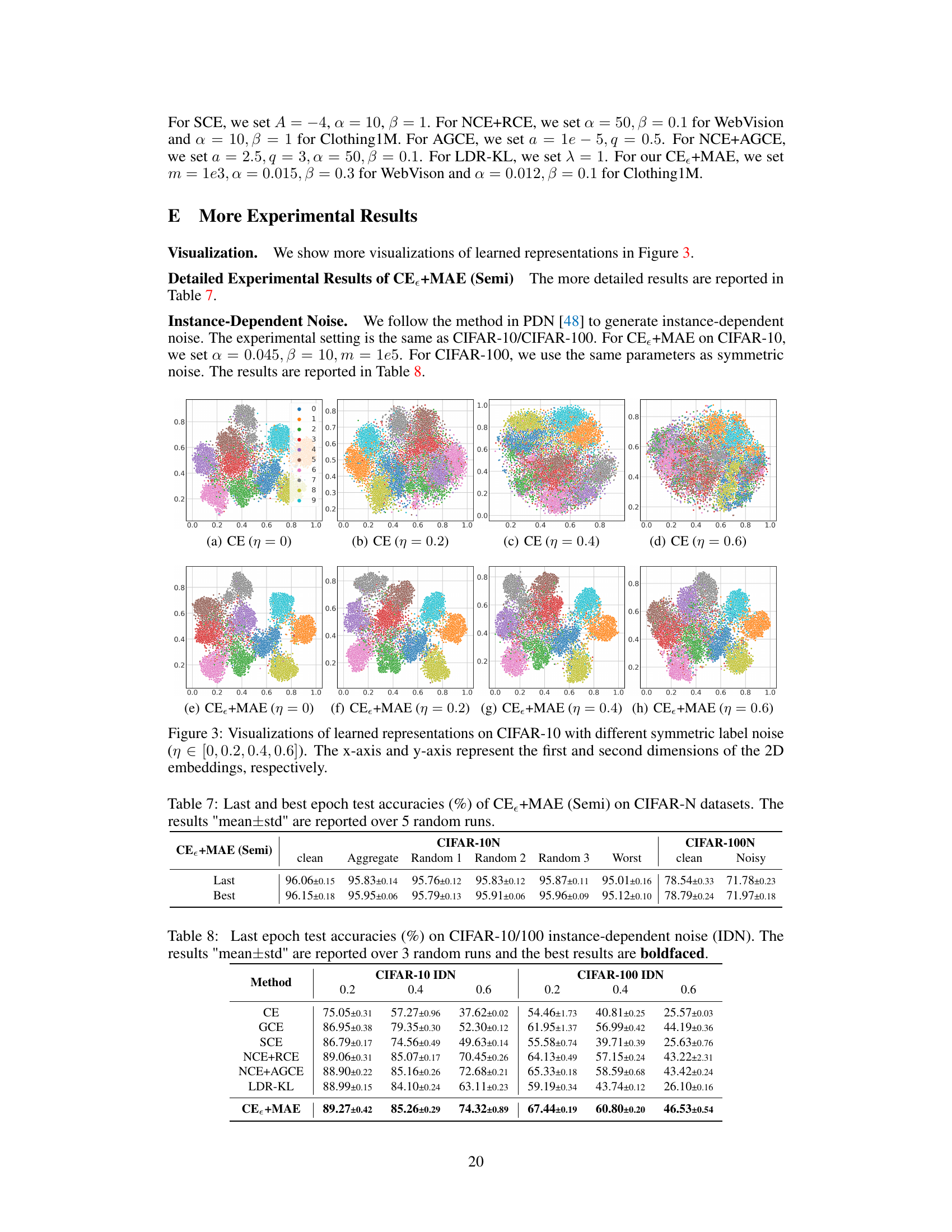
This figure visualizes the learned representations of CIFAR-10 data using t-SNE, comparing the standard Cross-Entropy (CE) loss and the proposed CE+MAE loss under different symmetric noise levels (0.2 and 0.4). The visualizations show that CE overfits to noisy labels and clusters are mixed, while CE+MAE generates well-separated clusters, indicating robustness to label noise.

This figure shows the test accuracy of the CE and CE+MAE loss functions with different values of the hyperparameter ’m’ under symmetric noise conditions on the CIFAR-10 dataset. The plots show that CE+MAE is more robust to noise than CE and is less prone to overfitting, especially at high noise levels. The zoomed-in sections highlight the performance in the last 20 epochs.
More on tables

This table summarizes the All-k consistency property of various loss functions. All-k consistency is a stronger property than standard consistency, indicating the loss function’s ability to achieve Bayes optimal top-k error for any k. A checkmark (✓) indicates All-k consistency, while an X indicates a lack thereof.

This table presents the test accuracies achieved by various methods on the CIFAR-10 and CIFAR-100 datasets under different symmetric and asymmetric noise conditions. The results, averaged over three random runs and reported as mean ± standard deviation, show the performance of various loss functions in handling noisy labels. The top two best performing methods for each condition are highlighted in bold.
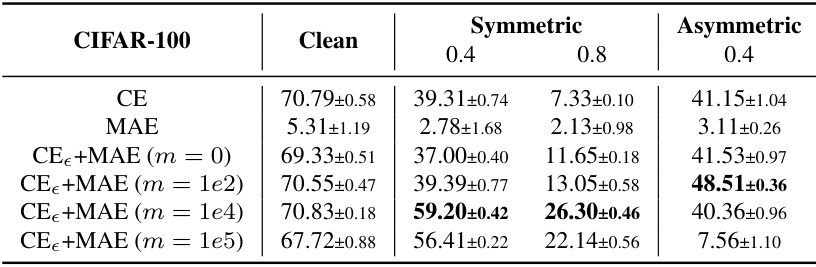
This table presents the results of ablation experiments conducted on the CIFAR-100 dataset to analyze the impact of the hyperparameter ’m’ in the CE+MAE loss function. The table compares the performance of CE+MAE with different values of ’m’ (including m=0, which is equivalent to the standard CE+MAE) across various noise levels (clean, symmetric noise rates of 0.4 and 0.8, and asymmetric noise rate of 0.4). The best performance for each noise level is highlighted in bold. The results show how the choice of ’m’ affects the trade-off between robustness to noise and the ability to fit clean data.
This table presents the test accuracies achieved by various methods on CIFAR-10 and CIFAR-100 datasets under different symmetric and asymmetric noise conditions. The results, averaged over three random runs, show the performance of different loss functions in handling label noise. The top two best-performing methods in each scenario are highlighted in bold.
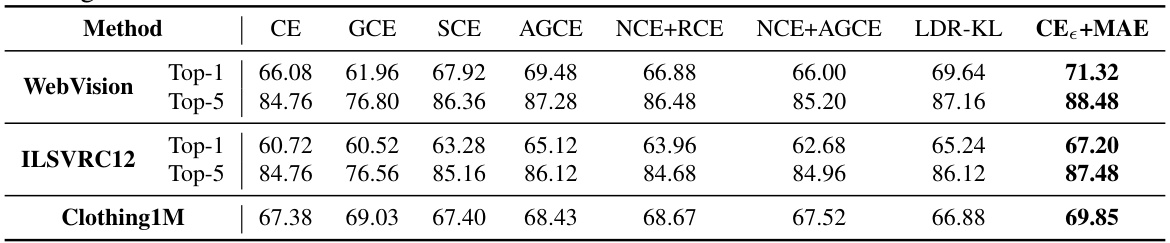
This table shows the test accuracy of various methods on CIFAR-10 and CIFAR-100 datasets under different symmetric and asymmetric noise conditions. The results are averaged over three independent runs, with standard deviations reported. The two highest-performing methods for each scenario are highlighted in bold.

This table presents the test accuracy results achieved by various methods on CIFAR-10 and CIFAR-100 datasets under different symmetric and asymmetric noise conditions. The results, expressed as mean ± standard deviation, were obtained across three independent runs. The top two best-performing methods for each noise level are highlighted in bold.

This table presents the test accuracies achieved by various methods (including the proposed method) on CIFAR-10 and CIFAR-100 datasets under different symmetric and asymmetric noise conditions. The results are averaged over three random runs, and the top two best performing methods are highlighted in bold for each scenario.

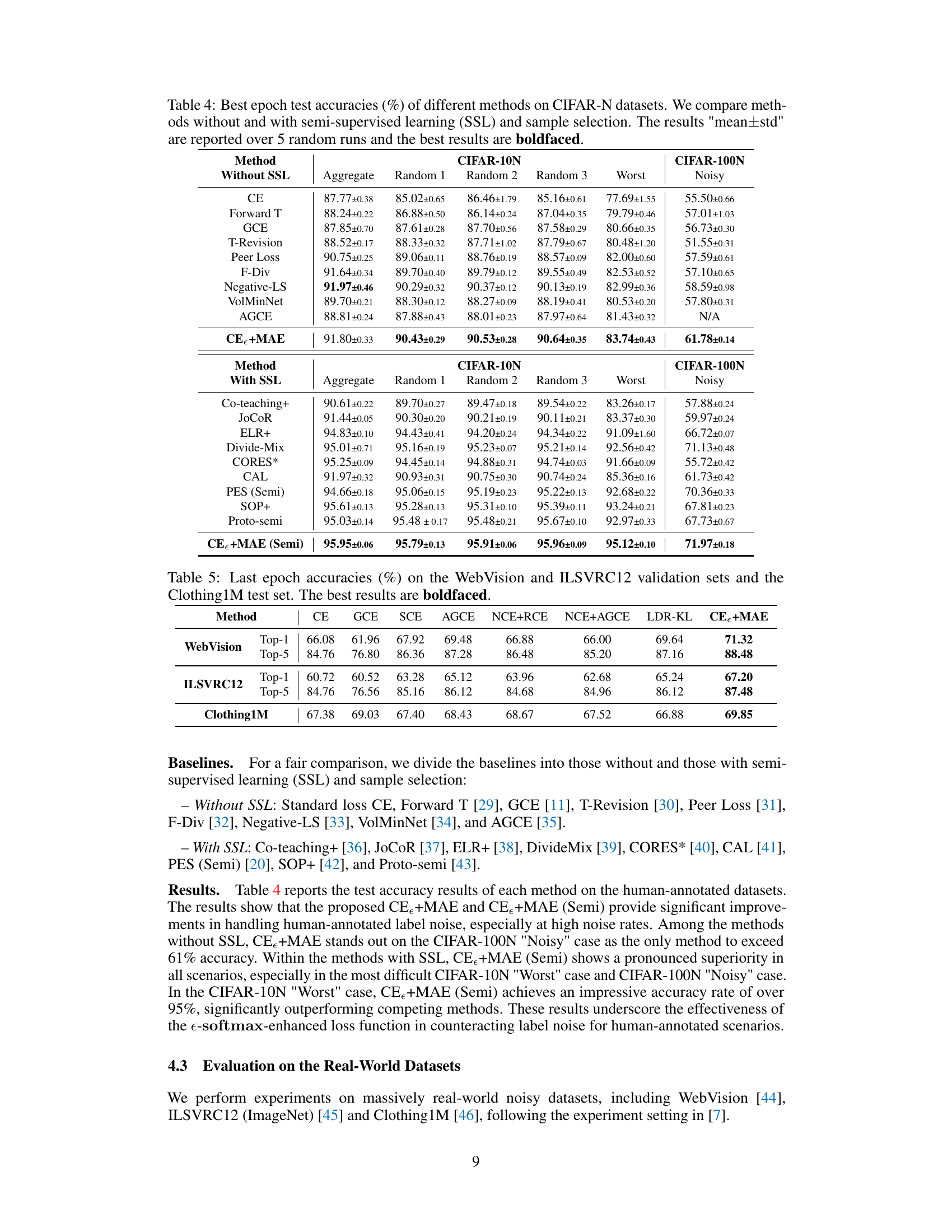
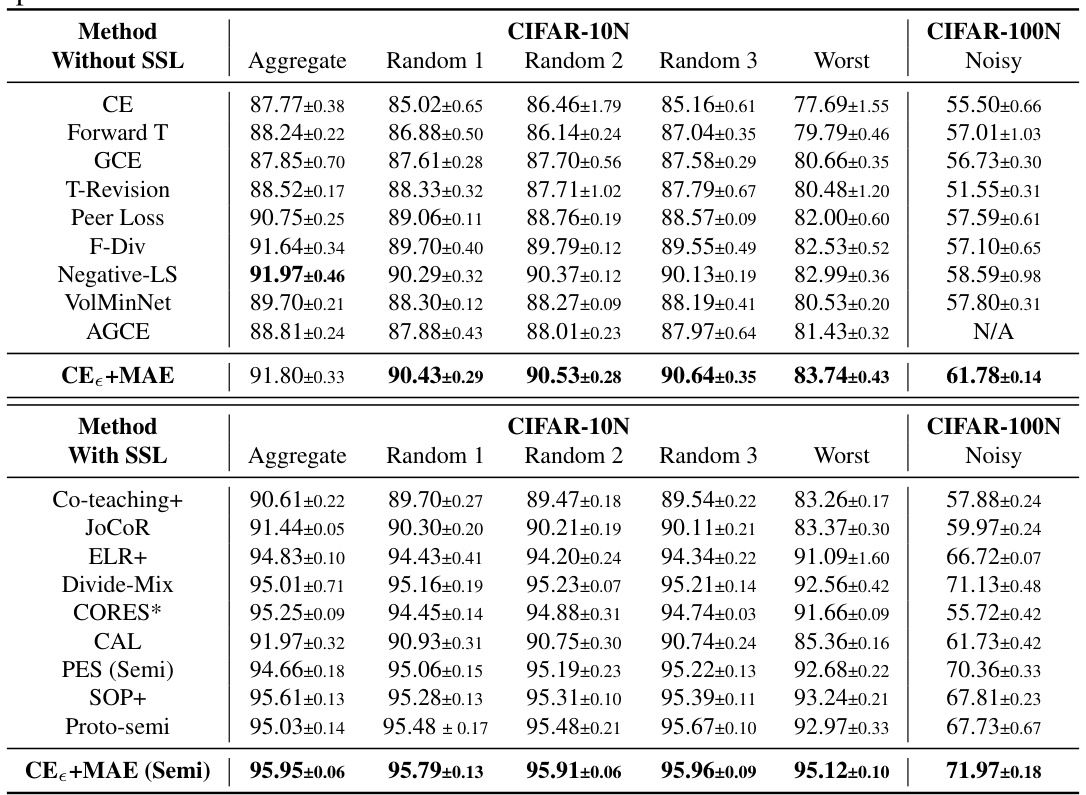
This table compares the performance of various methods on CIFAR-10N and CIFAR-100N datasets, which are datasets with human-annotated noisy labels. It shows the test accuracy of methods both with and without semi-supervised learning (SSL) and sample selection techniques. The best performing methods are highlighted in bold. The results are averaged over 5 runs, with the standard deviation reported.
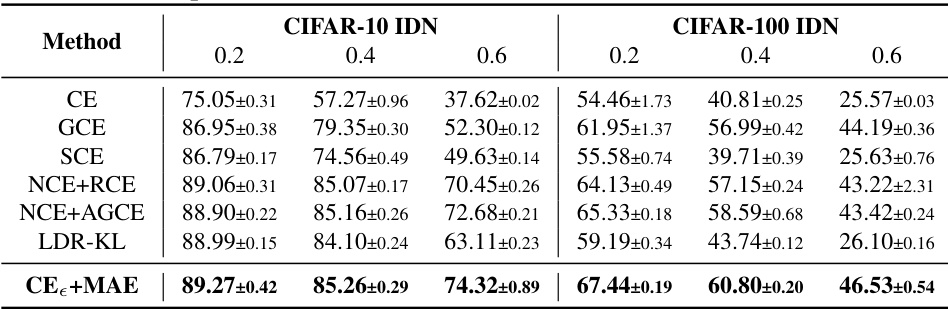
This table presents the last epoch test accuracies of different methods on CIFAR-10 and CIFAR-100 datasets with instance-dependent noise. The results are averaged over three random runs, and the standard deviation is reported. The best results in each setting are highlighted in bold.
Full paper#