Large Pre-trained time series models for cross-domain Time series analysis tasks

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in time series analysis due to its introduction of LPTM, a novel multi-domain pre-trained model. LPTM’s superior performance with less data and training time opens exciting avenues for research in cross-domain generalization, particularly using adaptive segmentation strategies for improved tokenization of time series data. Its impact on various downstream tasks makes it highly relevant to current trends in foundational modeling and data-efficient learning.

Visual Insights

#

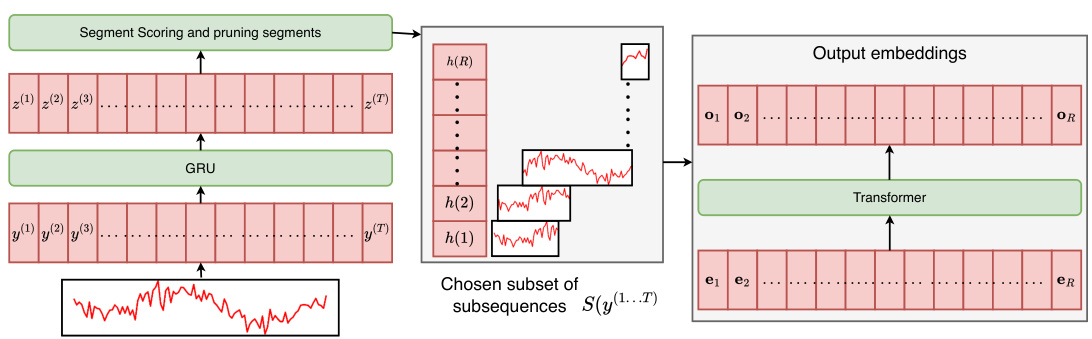
This figure illustrates the architecture of the Large Pre-trained Time-series Models (LPTM). The input time series is first segmented using an adaptive segmentation module guided by a scoring function that aims to minimize the self-supervised learning (SSL) loss. These segments, acting as tokens, are then fed into a transformer encoder. The encoder’s output embeddings are used for various downstream time series analysis tasks.

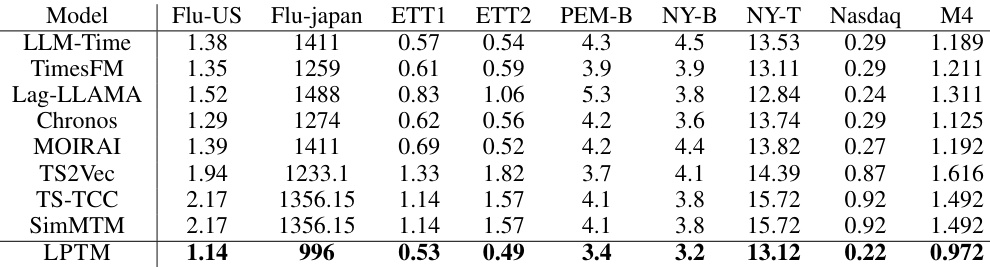
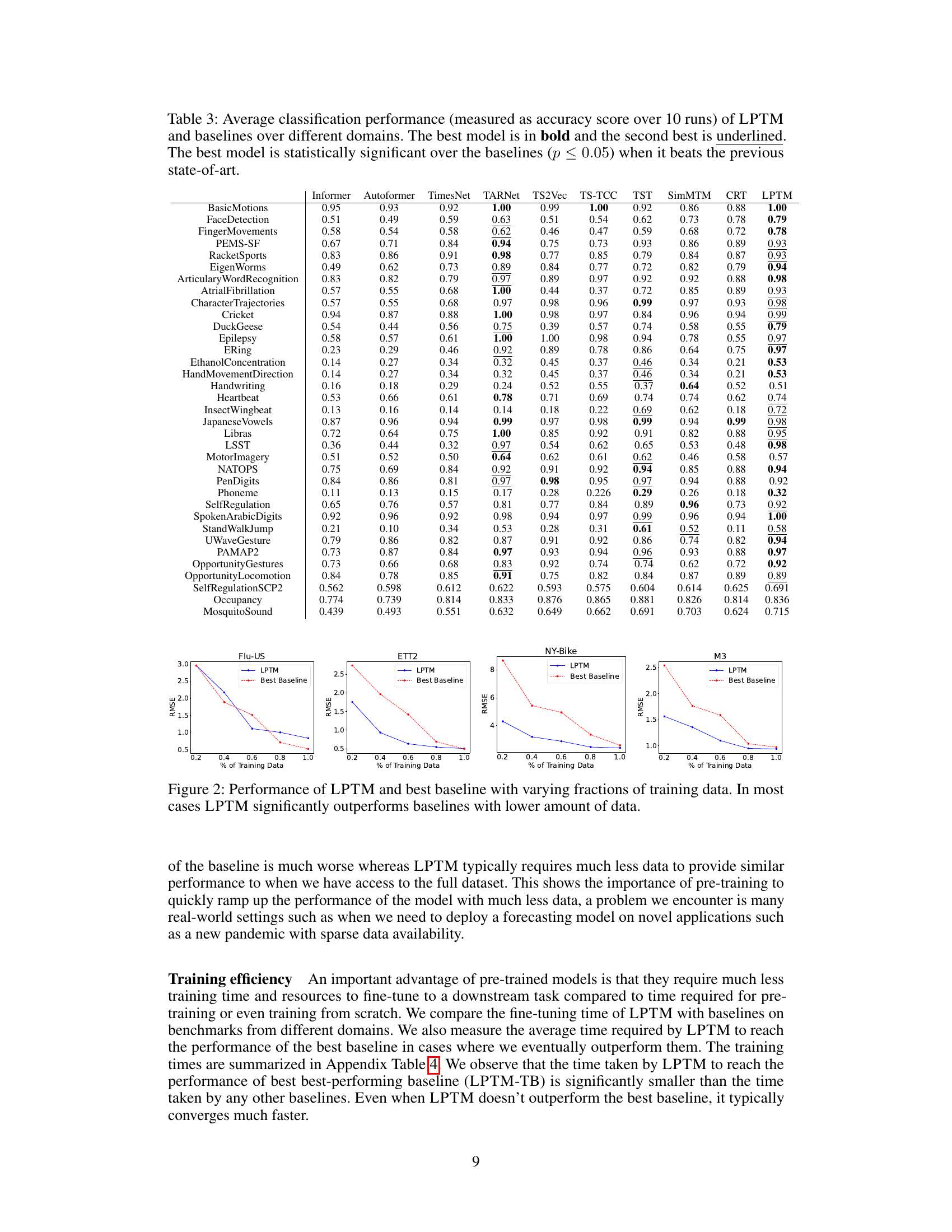
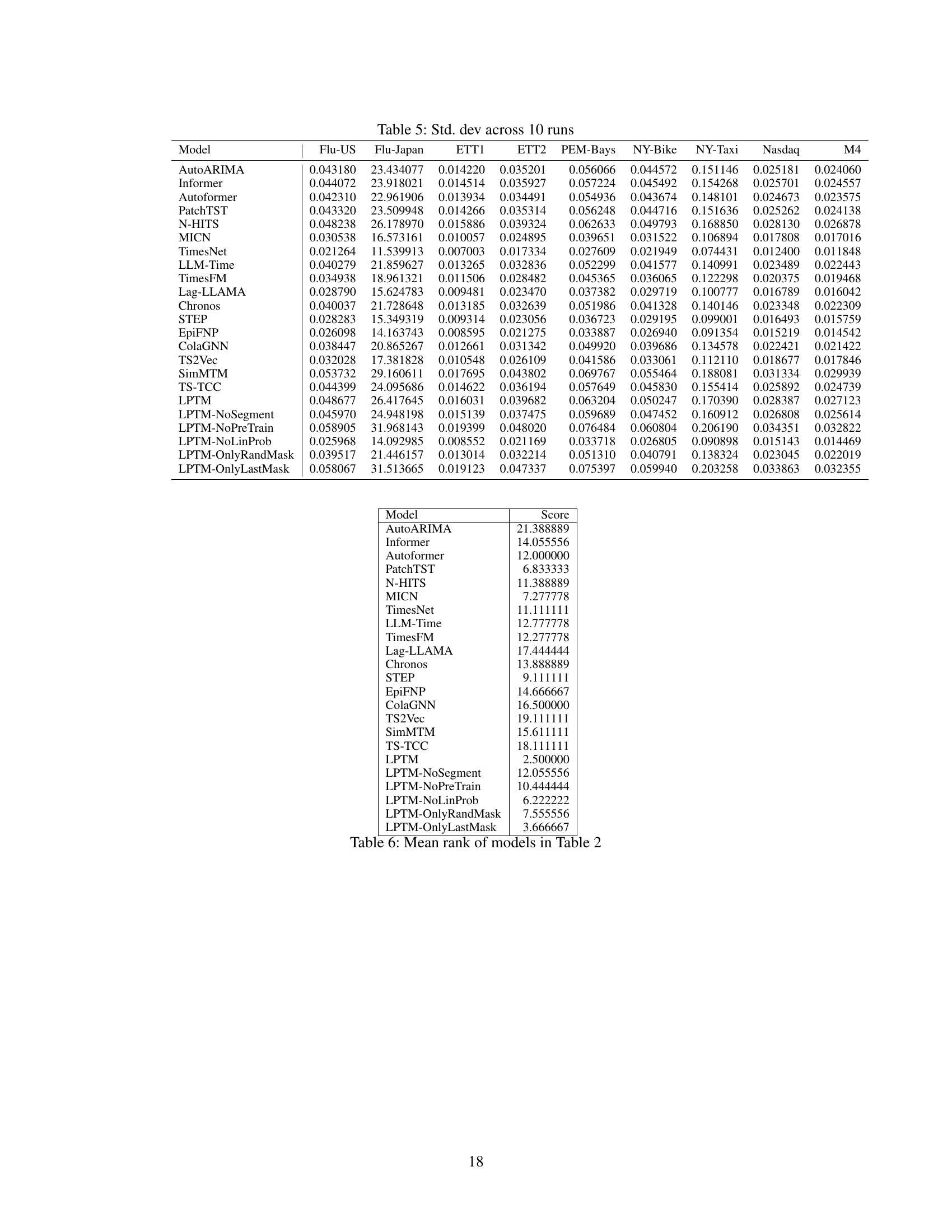
This table presents a comparison of the root mean squared error (RMSE) achieved by LPTM and several other pre-trained baselines across multiple time series forecasting tasks. The performance is evaluated under zero-shot conditions, meaning that no further fine-tuning of the pre-trained models was performed before testing on the benchmarks. The results are averaged over 10 independent runs to ensure reliability, and the best performing model for each task is highlighted in bold.

In-depth insights

#

Adaptive Segmentation

#

The concept of ‘Adaptive Segmentation’ in time series analysis is crucial for handling the variability inherent in real-world data. Traditional fixed-length segmentation methods fail to capture the diverse temporal dynamics present in different datasets. An adaptive approach is necessary to identify optimal segment lengths based on the data’s characteristics, such as sampling rate, noise levels, and underlying patterns. The core idea is to learn a segmentation strategy that maximizes performance on a downstream task (e.g., forecasting, classification). This often involves a scoring mechanism that evaluates potential segments, maybe via self-supervised learning, selecting segments that improve the model’s performance. Adaptive segmentation, therefore, allows the model to learn useful temporal patterns at the right scale, enhancing its ability to generalize across diverse time series datasets and improving prediction accuracy. A key challenge is developing effective scoring functions that generalize well across various time series and designing a mechanism to integrate these learned segmentations efficiently within the overall model architecture.

Multi-Domain Pretraining

#

Multi-domain pretraining in the context of time series analysis presents a powerful paradigm shift. Instead of training separate models for each domain (e.g., finance, healthcare, climate), a single model is pretrained on a diverse range of time series data, allowing it to learn generalizable features and patterns. This approach offers significant advantages, including improved efficiency by reducing the need for extensive domain-specific training data and enhanced generalizability, enabling the model to perform well on unseen domains. However, challenges exist: ensuring meaningful data representation across heterogeneous datasets (with varying sampling rates, granularities, and noise levels) requires careful consideration. A key aspect is effective segmentation of time series, which must be adaptive to the characteristics of different domains. A successful multi-domain pretraining strategy needs to address this and carefully consider model architecture to effectively capture transferable knowledge while avoiding negative transfer. The resulting model should ideally be capable of zero-shot or few-shot adaptation, requiring minimal domain-specific fine-tuning.

Zero-Shot Forecasting

#

Zero-shot forecasting, a key capability highlighted in the research paper, signifies a model’s ability to predict future trends without prior training on the specific target data. This is a significant advancement, especially considering the resource-intensive nature of traditional time-series model training. The success of zero-shot forecasting rests on the model’s capacity to learn generalizable patterns during pre-training across diverse datasets. This generalizability enables the model to adapt to unseen datasets and domains, effectively making forecasting more efficient and broadly applicable. However, the paper also acknowledges potential limitations in terms of accuracy compared to fine-tuned models, particularly when dealing with data exhibiting unique dynamics. The research demonstrates that the adaptive segmentation approach and multi-domain pre-training significantly enhance the model’s ability to perform zero-shot forecasting. This approach effectively captures nuanced temporal patterns and allows the model to function effectively without task-specific training. This ability to generalize and perform adequately without fine-tuning on the target domain significantly improves the efficiency and scalability of time-series forecasting.

Data Efficiency Gains

#

The concept of ‘Data Efficiency Gains’ in machine learning research centers on achieving high performance with significantly less training data. This is crucial because acquiring and labeling large datasets can be expensive and time-consuming. A model exhibiting data efficiency gains would require fewer data points to achieve comparable or better accuracy than existing state-of-the-art models. This efficiency can stem from improved model architectures, better training algorithms (such as transfer learning or self-supervised learning), or more effective data preprocessing techniques. The advantages are numerous, including reduced costs, faster training times, and the potential to apply machine learning to scenarios with limited data availability. Quantifying these gains often involves comparing the model’s performance against baselines using various metrics like accuracy, precision, recall, and F1-score across different datasets. This can highlight the practical significance of a data-efficient model and its potential impact on resource-constrained applications.

Future Work: Scalability

#

Future work on scalability for large pre-trained time series models (LPTMs) presents exciting opportunities and significant challenges. Addressing the computational cost of training and fine-tuning LPTMs on massive datasets is paramount. This could involve exploring more efficient training algorithms, model compression techniques, and distributed training strategies across multiple GPUs or cloud computing resources. Furthermore, improving the efficiency of the adaptive segmentation module is crucial for handling high-frequency or extremely long time series data. Research into new segmentation strategies that balance semantic meaning with computational cost is vital. Extending LPTM’s applicability to multivariate time series would significantly broaden its impact. This would require developing effective methods for handling high-dimensional data and complex interdependencies between multiple variables. Finally, rigorous testing of LPTM’s performance on diverse real-world datasets across different domains is essential to validate its generalizability and robustness before widespread deployment.

More visual insights

#

More on figures

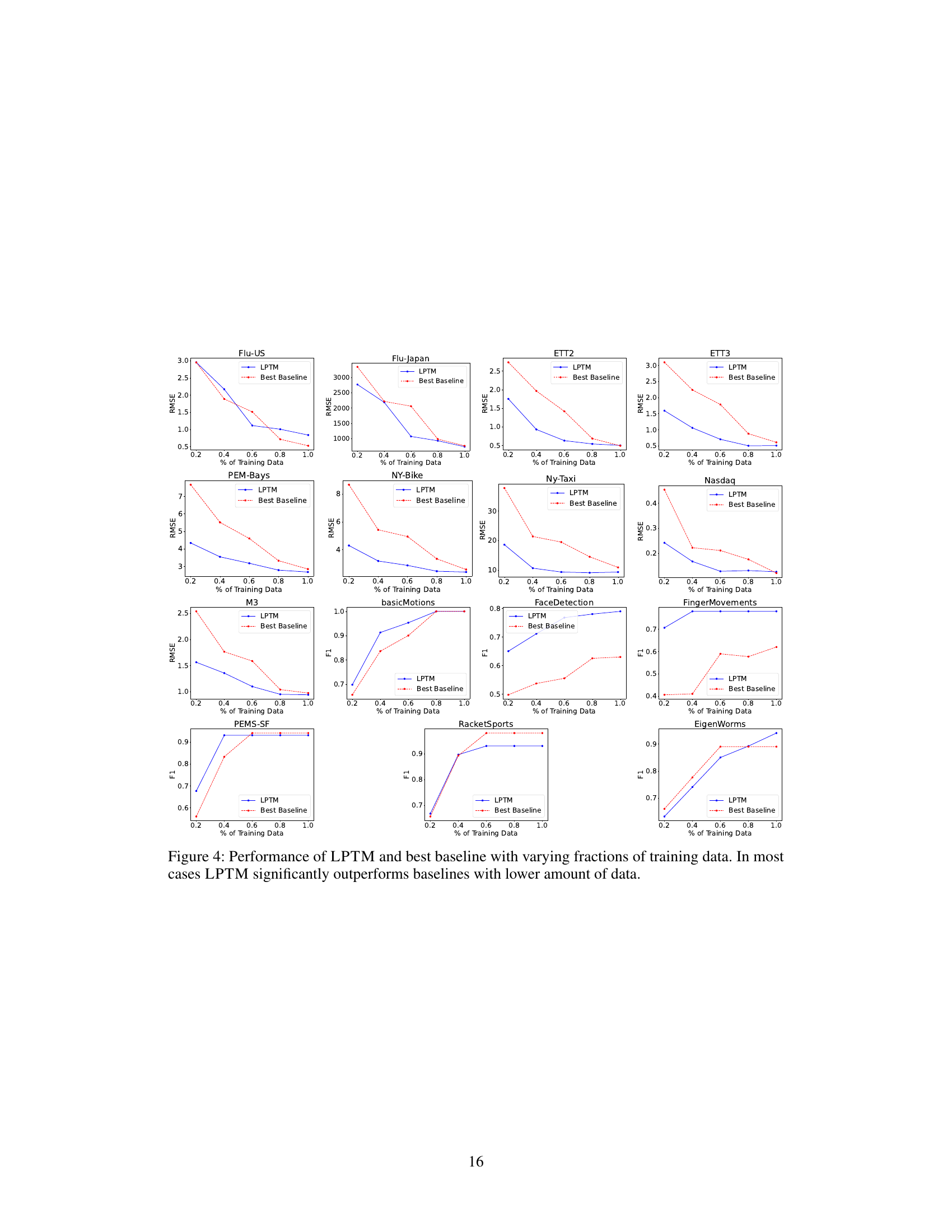
This figure compares the performance of LPTM and the best-performing baseline model for several time-series forecasting tasks, when trained on varying percentages of the available training data. The x-axis represents the percentage of training data used, ranging from 20% to 100%. The y-axis displays the Root Mean Squared Error (RMSE), a common metric for evaluating the accuracy of time-series forecasts. Lower RMSE values indicate better forecasting accuracy. The figure showcases that LPTM consistently achieves lower RMSE values than the baselines across various datasets, demonstrating its superior performance even when trained on significantly less data.

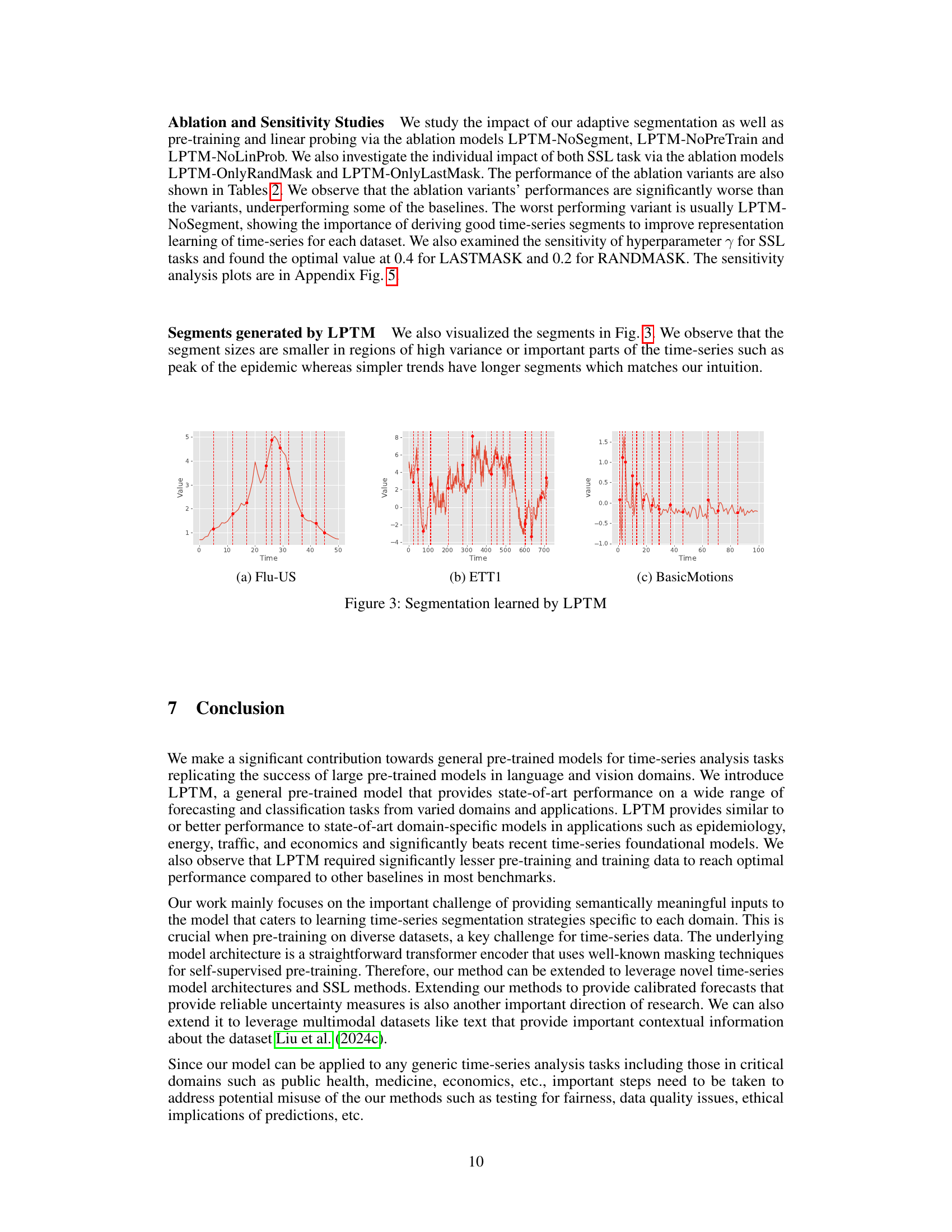
This figure visualizes the segmentation strategy learned by the LPTM model for three different time series datasets: Flu-US, ETT1, and BasicMotions. The red dots represent the segment boundaries identified by the adaptive segmentation module of LPTM. The plots show that the model learns to segment the time series based on the underlying dynamics. In regions with high variance or important temporal patterns, such as the peak of an epidemic (Flu-US), the segments are shorter and more frequent, capturing the intricate details of the time series. In contrast, simpler trends, such as the smoother patterns in ETT1, have longer segments. This adaptive segmentation enables LPTM to effectively capture both local and global temporal patterns within the time series, improving its overall performance.

This figure visualizes the segmentations learned by the LPTM model for different time series datasets. It shows how the adaptive segmentation module identifies variable-length segments, with shorter segments in regions of high variance or significant events (like the peak of an epidemic) and longer segments in smoother areas. This highlights the model’s ability to adapt to the varying characteristics of different time series.

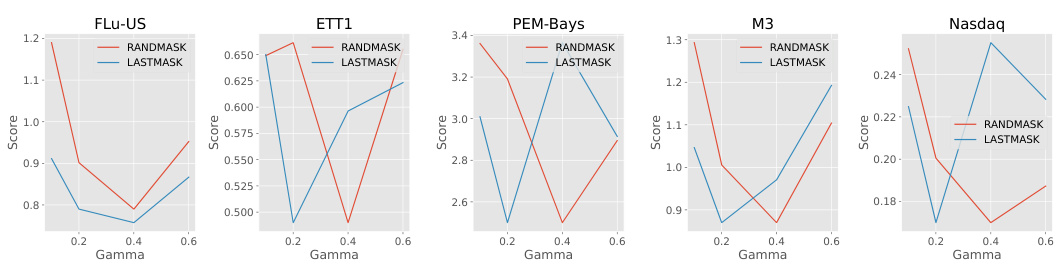
This figure visualizes the segmentation strategy learned by the LPTM model for three different time series datasets: Flu-US, ETT1, and BasicMotions. The x-axis represents time, and the y-axis represents the value of the time series. Each colored segment represents a segment identified by the adaptive segmentation module. The lengths of the segments vary depending on the complexity of the time series patterns within each domain. In domains with smoother trends, the segments are longer. In domains with more complex, rapidly changing trends, the segments are shorter. This demonstrates the adaptive nature of the segmentation module in handling the diversity and variability found in real-world time series data.

More on tables

This table presents a comparison of the root mean squared error (RMSE) achieved by the proposed LPTM model and several pre-trained baseline models on eight different forecasting tasks. The performance is evaluated under zero-shot settings, meaning the models are not fine-tuned for any specific task before evaluation. The best-performing model for each task is highlighted in bold.

This table presents the results of a zero-shot forecasting experiment comparing the performance of the proposed Large Pre-trained Time-series Model (LPTM) against several pre-trained baseline models across various time series forecasting tasks. The performance metric used is the Root Mean Squared Error (RMSE), averaged across 10 runs for each model and task. The tasks are performed without any fine-tuning of the models, hence the term ‘zero-shot’. The best performing model for each task is highlighted in bold.

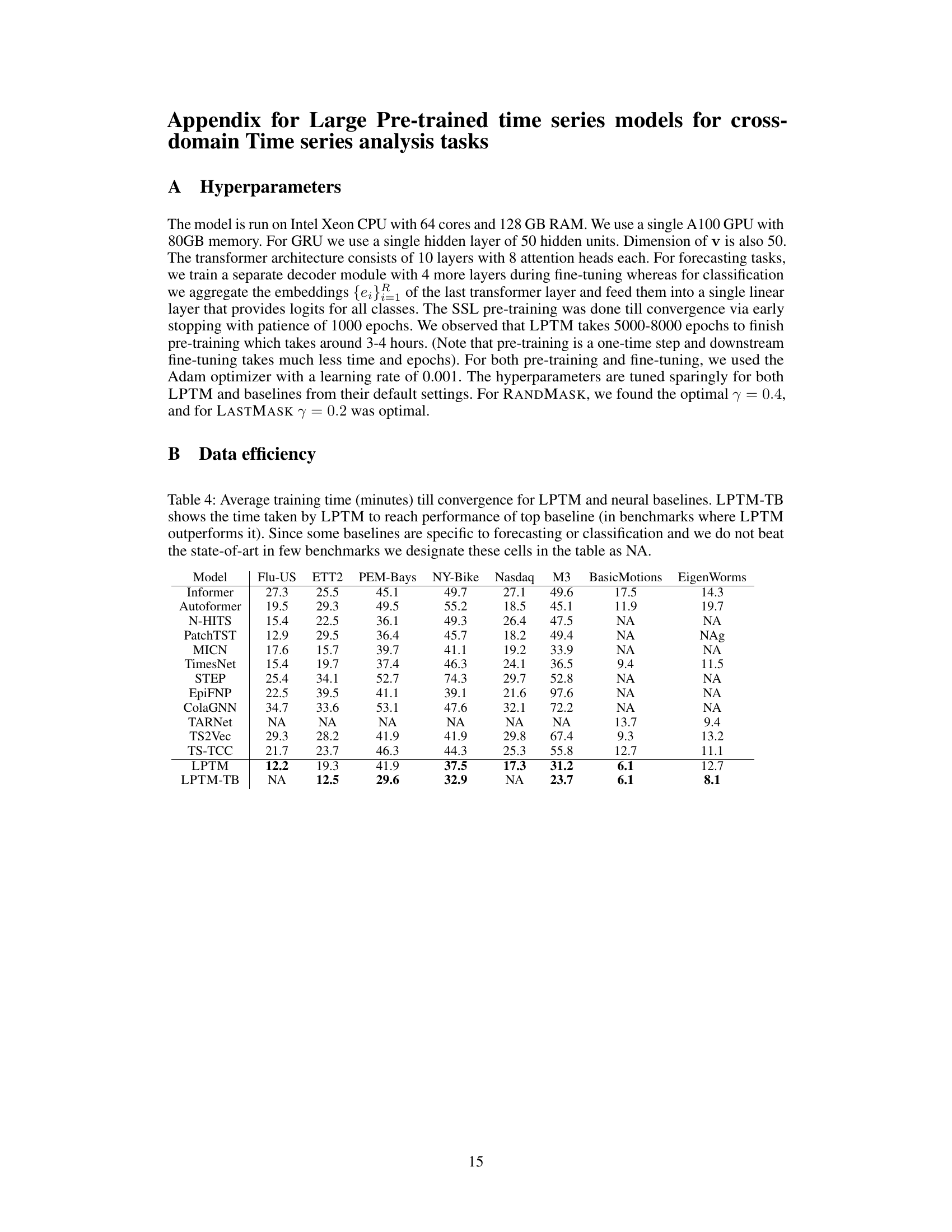
This table presents the average training time in minutes until convergence for the LPTM model and several neural baseline models across various time series forecasting and classification tasks. The models are evaluated on their performance on eight different datasets, and the training time is shown for each. The LPTM-TB column shows the time taken by LPTM to achieve the performance of the best baseline model in the cases where LPTM outperforms the other baselines.

This table presents the results of a zero-shot forecasting experiment comparing the performance of the proposed LPTM model against several pre-trained baselines across multiple datasets. The performance metric is the Root Mean Squared Error (RMSE), averaged over 10 runs. The best performing model for each dataset is highlighted in bold.

This table presents the results of a zero-shot forecasting experiment comparing the performance of the proposed Large Pre-trained Time-series Model (LPTM) against several state-of-the-art pre-trained baselines. The performance metric used is Root Mean Squared Error (RMSE), averaged over 10 independent runs. The models were evaluated on eight different forecasting tasks across various domains, including influenza forecasting, electricity demand, and traffic flow. The best performing model for each task is highlighted in bold.

Full paper

#