↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
The brain uses Bayesian inference to make decisions under uncertainty, but how this occurs in neural circuits is unclear. Most models oversimplify by ignoring the diverse types of inhibitory neurons present in actual brain circuitry, which are known to affect neural activity in different ways. This makes it difficult to understand how the brain performs Bayesian computations efficiently.
This research builds a detailed computational model of a canonical brain circuit that includes the major types of inhibitory neurons, PV and SOM. Through rigorous mathematical analysis, they reveal how the circuit performs Bayesian inference. Specifically, the circuit uses Langevin sampling (with PV neurons) and Hamiltonian sampling (with the addition of SOM neurons). The addition of SOM neurons accelerates sampling speed because Hamiltonian sampling is inherently more efficient than Langevin sampling. Importantly, their results suggest that for proper Hamiltonian sampling, SOM neurons should not receive direct feedforward sensory inputs, aligning with known neuroanatomy.
Key Takeaways#
Why does it matter?#
This paper is crucial because it bridges the gap between theoretical Bayesian models and the complex reality of cortical circuits. By incorporating diverse inhibitory interneurons, it offers a more biologically realistic framework for understanding Bayesian inference in the brain. This opens new avenues for research into neural computation and provides valuable insights for building more accurate and efficient artificial intelligence systems.
Visual Insights#
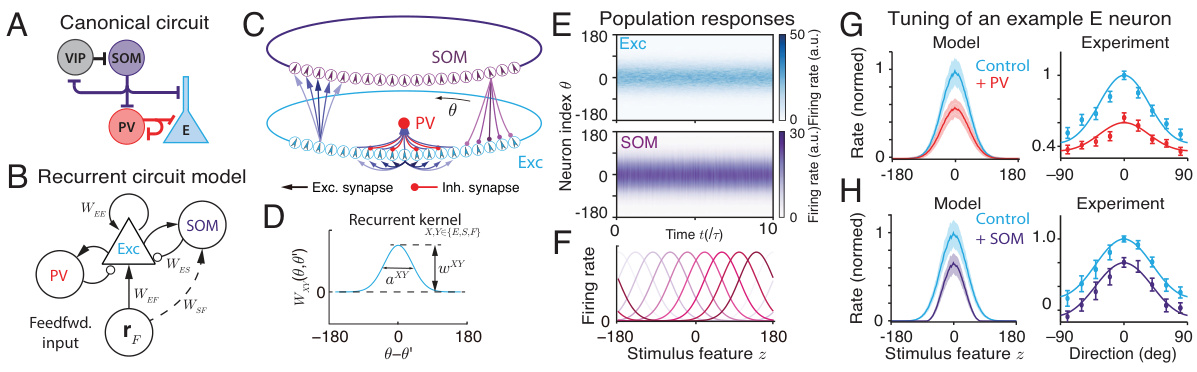
This figure illustrates a recurrent neural circuit model incorporating excitatory (E) neurons and two types of inhibitory interneurons: parvalbumin (PV) and somatostatin (SOM). Panel (A) shows a schematic of the canonical cortical circuit with its three major inhibitory interneuron types. Panels (B) and (C) detail the model’s structure, showing the connections between neuron types and the Gaussian recurrent connection kernels. Panel (D) displays these kernels. Panel (E) presents example population responses of E and SOM neurons over time. Panel (F) shows the tuning curves of the E neurons. Finally, Panels (G) and (H) compare the tuning curves of an example E neuron in the model and experimental data, demonstrating the effects of adding PV and SOM inhibition, respectively.
In-depth insights#
Bayesian Sampling#
The concept of Bayesian sampling, central to the research paper, focuses on how neural circuits might perform probabilistic inference. The paper investigates how the diversity of inhibitory interneurons within canonical recurrent circuits influences this sampling process. A key finding highlights the role of distinct interneuron types (PV and SOM) in shaping the efficiency of Bayesian inference. The model suggests that the circuit dynamics transition from Langevin sampling (with PV neurons only) to a more efficient Hamiltonian sampling (when SOM neurons are incorporated), improving sampling speed. The theoretical framework elegantly connects circuit dynamics with Bayesian algorithms, offering valuable insight into how the brain might implement these computations. Crucially, the model’s predictions regarding the lack of direct feedforward input to SOM neurons are consistent with neuroanatomical findings. The study deepens our understanding of how neural circuitry underpins Bayesian brain hypotheses, suggesting a complex interplay between excitatory and diverse inhibitory neuronal populations.
Circuit Dynamics#
The theoretical analysis of circuit dynamics is a cornerstone of the research, focusing on how the interplay of excitatory (E) and inhibitory (I) neurons, specifically Parvalbumin (PV) and Somatostatin (SOM) interneurons, shapes the overall network behavior. The model’s nonlinear dynamics are investigated using perturbation analysis, revealing a low-dimensional stimulus feature manifold where the circuit’s essential activity is captured. A reduced circuit model, incorporating only E and PV neurons, demonstrates Langevin sampling, a fundamental Bayesian inference algorithm. The inclusion of SOM neurons enhances sampling efficiency by upgrading the Langevin dynamics to a Hamiltonian framework, accelerating convergence towards the posterior distribution. This transition hinges on the tuning properties of SOM neurons and their connectivity, highlighting the crucial role of interneuron diversity in optimal Bayesian inference. The model demonstrates flexibility in sampling various posterior distributions by adjusting input parameters and weights, showcasing the circuit’s adaptability to handle uncertainty. Finally, analysis of the eigenvalues of the circuit’s dynamic matrix provides insight into the sampling speed and temporal correlations of generated samples, thus quantifying the impact of inhibitory neuron subtypes on inference efficiency.
Interneuron Roles#
The roles of inhibitory interneurons in cortical circuits are multifaceted and crucial for shaping network dynamics and computations. Parvalbumin (PV) interneurons, with their broad connectivity and fast spiking, provide global inhibition, primarily acting as a divisive normalization mechanism to stabilize network activity and maintain balanced excitation-inhibition. In contrast, somatostatin (SOM) interneurons exhibit more localized connectivity and slower spiking, contributing to tuning-dependent inhibition which influences stimulus selectivity and response properties. The interplay between PV and SOM interneurons, with their differing connectivity and response dynamics, is crucial for shaping the circuit’s computation of Bayesian inference, as demonstrated in the paper. The study highlights how the combination of global and local inhibition significantly influences the sampling algorithm, leading to more efficient Bayesian computations.
Hamiltonian Speedup#
The concept of “Hamiltonian Speedup” in the context of Bayesian sampling within neural circuits suggests that incorporating diverse inhibitory interneuron types, specifically Somatostatin (SOM) neurons, can significantly enhance the efficiency of the sampling process. The key insight lies in the transition from Langevin dynamics (a first-order process) to Hamiltonian dynamics (a second-order process) through the inclusion of SOM neurons. Langevin dynamics, while capable of sampling, can be slow and prone to getting stuck in local minima. Hamiltonian dynamics, by introducing an auxiliary momentum variable representing the influence of SOM neurons, enables more efficient exploration of the probability landscape, thereby accelerating convergence to the target distribution. The non-monotonic effect of SOM inhibition further indicates a delicate interplay between the model parameters and the efficiency of Bayesian inference. This observation underscores the nuanced role of inhibitory interneuron diversity in shaping the computational capabilities of neural circuits, highlighting its potential to optimize information processing in the brain.
Future Research#
Future research directions stemming from this Bayesian sampling in canonical recurrent circuits study could fruitfully explore several avenues. Investigating the role of VIP interneurons in the circuit model is crucial, as they modulate SOM neuron activity and could significantly impact sampling dynamics. This would refine the understanding of the interplay between different inhibitory neuron types in Bayesian inference. Furthermore, extending the model to handle dynamic stimuli presented as a hidden Markov model would significantly advance its biological realism and allow analysis of temporal aspects of Bayesian computations. Another promising direction is developing a better understanding of how non-uniform priors are encoded and implemented in the circuit. While the current model uses a uniform prior, cortical circuits likely implement various prior distributions. Finally, exploring the relationship between circuit connectivity parameters and the performance of Bayesian sampling under different noise conditions would strengthen the robustness and validity of the model. Specifically, testing the model’s performance with heterogeneous neuron populations and non-translation invariant connectivity will elucidate its behavior under more realistic biological conditions.
More visual insights#
More on figures
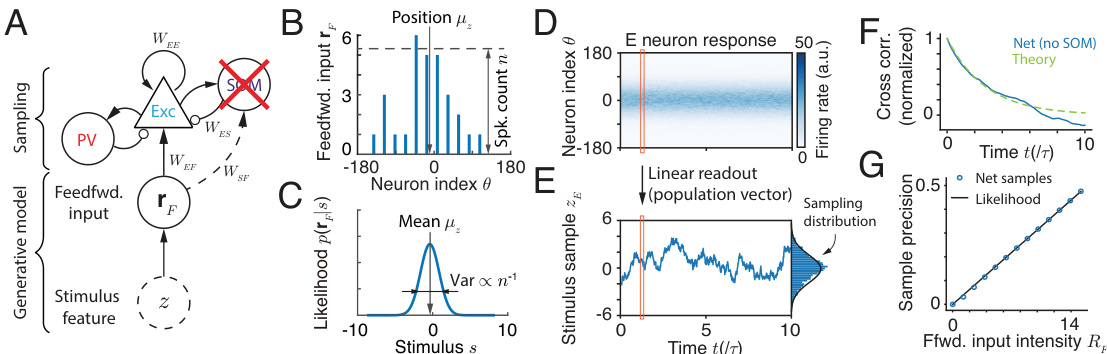
This figure illustrates the reduced circuit model without SOM neurons, showing the feedforward input, linear readout, E neuron population responses, stimulus sample generation, cross-correlation of samples, and flexible sampling of posteriors with varying uncertainties. It visually explains how the model generates samples that approximate a Bayesian posterior distribution.

This figure demonstrates the Bayesian sampling process in a neural circuit model incorporating PV and SOM interneurons. Panel A shows the population responses of excitatory (E) and SOM neurons over time. Panel B illustrates how the network’s sampling distribution is obtained from both neuron types. The distribution of samples from E neurons approximates the posterior distribution. Panels C and D demonstrate the effects of adding SOM neurons. Notably, panel D shows a linear relationship between feedforward weight and SOM inhibition which ensures correct posterior sampling. Lastly, Panel E shows that with fixed weights, the circuit effectively samples posteriors with varying levels of uncertainty.
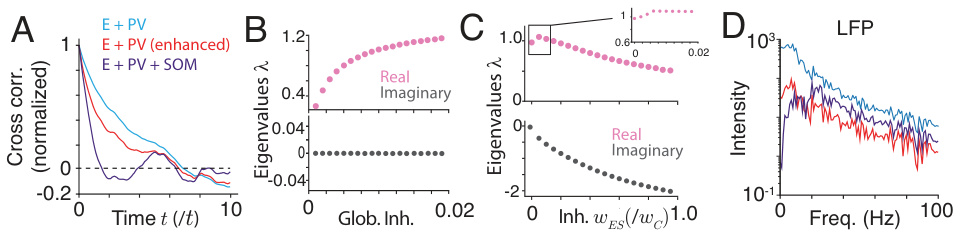
This figure analyzes the impact of PV and SOM interneuron manipulations on the sampling process. Panel A shows the cross-correlation of samples generated by the network under different conditions (E+PV, enhanced E+PV, and E+PV+SOM). Panels B and C illustrate the effect of PV (global) and SOM (local) inhibition strength on the real and imaginary parts of the smallest eigenvalue of the sampling dynamics. Panel D displays the local field potential (LFP) power spectra for the same conditions.
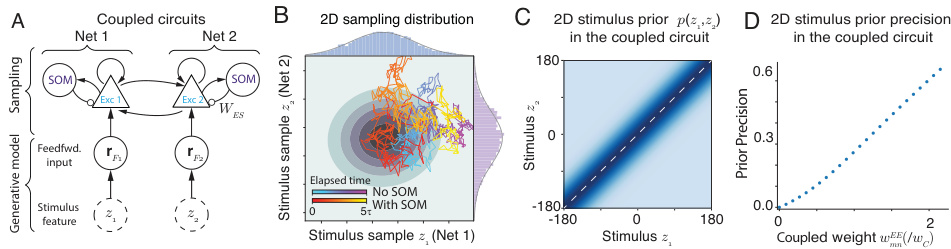
Figure 5 demonstrates how the model can be extended to sample high-dimensional stimulus posteriors by using coupled circuits. Each circuit is identical to the one in Figure 1B, except that PV neurons are omitted for simplicity. Two circuits are coupled, where the excitatory neurons of each circuit receive input from the other. Each circuit receives feedforward input corresponding to a distinct latent stimulus feature. Panel A shows a schematic of this coupled circuit setup. Panel B shows the resulting 2D sampling distribution, which demonstrates the network’s capacity to sample from a bivariate posterior. Panels C and D quantitatively characterize the prior distribution encoded in this coupled system. Panel C depicts the 2D stimulus prior that emerges from the coupling. Panel D illustrates that the precision of this prior increases with the strength of the coupling weights.
Full paper#



















