Remix-DiT: Mixing Diffusion Transformers for Multi-Expert Denoising

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it presents Remix-DiT, a novel and efficient method for multi-expert denoising in diffusion models. It addresses the high computational cost associated with large transformer models by cleverly mixing a smaller number of basis models to create many experts, improving generation quality without increasing inference overhead. This offers significant advantages for researchers working on improving the efficiency and performance of diffusion models, opening avenues for further exploration in multi-expert learning and adaptive model capacity allocation.

Visual Insights

#

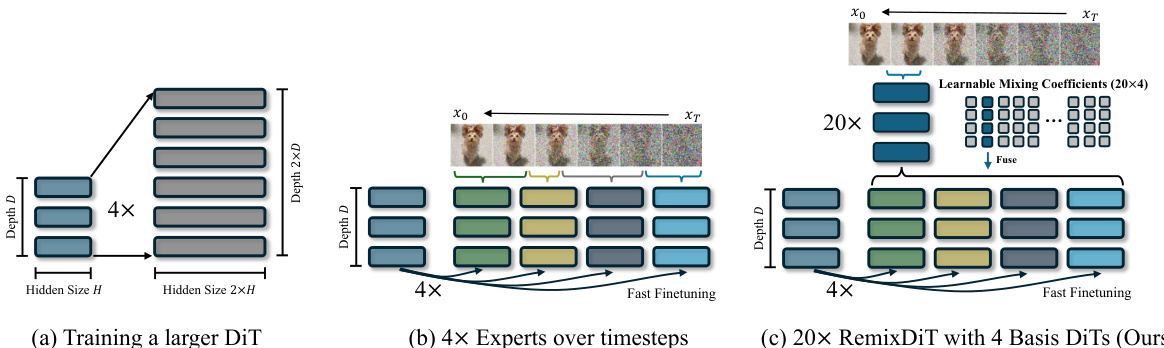
This figure illustrates three different approaches to improving the quality of diffusion models. (a) shows the traditional approach of simply increasing the size of the model. This is expensive in terms of training and inference costs. (b) shows a multi-expert approach where multiple smaller models are trained to handle different parts of the denoising process. This reduces the overhead of training and inference but still incurs significant training costs due to training multiple models. (c) shows the proposed RemixDiT approach. This uses learnable mixing coefficients to combine a smaller number of basis models to create a larger number of experts. This reduces training costs while maintaining efficiency.

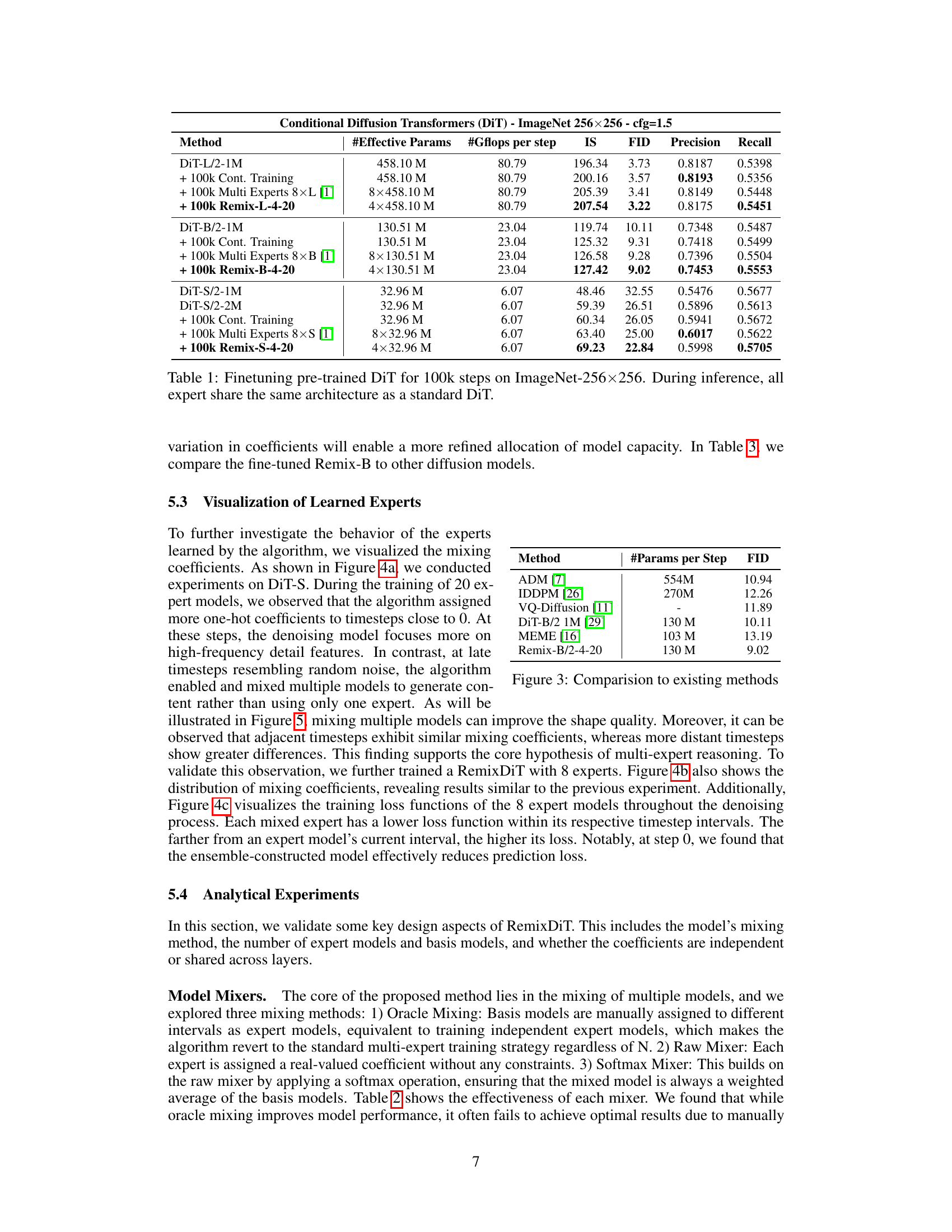
This table presents the results of fine-tuning standard DiT models (DiT-L, DiT-B, DiT-S) using the Remix-DiT approach with 100k training steps. It compares the performance of the standard DiT models against those fine-tuned using continual training and multi-expert methods. The Remix-DiT models demonstrate improvements in terms of Inception Score (IS), Fréchet Inception Distance (FID), Precision, and Recall metrics, showcasing its effectiveness in enhancing model performance even with a limited training budget.

In-depth insights

#

Multi-Expert Remix

#

A hypothetical ‘Multi-Expert Remix’ section in a research paper would likely explore methods for combining multiple specialized models, or “experts,” to improve performance. This could involve techniques like gating mechanisms, which selectively activate different experts based on input characteristics, or weighted averaging, where the outputs of multiple experts are combined based on learned weights. The “remixing” aspect suggests an adaptive or dynamic approach, possibly learning to adjust the weights or gating decisions during inference, or even changing the set of active experts throughout a process. A key challenge would be balancing the increased model complexity (and potentially computational cost) against the potential gains in accuracy or efficiency. The section should present the specific remixing strategy employed, a thorough evaluation of its efficacy compared to single-expert or other multi-expert baselines, and a discussion of the strategy’s limitations and potential for extension to different tasks or model architectures. Learnable parameters are likely to play a crucial role in adapting the remixing strategy during training. The results section would demonstrate the efficacy of the proposed method, highlighting its ability to improve over single experts on complex tasks while controlling computational overhead.

Adaptive Mixing

#

Adaptive mixing, in the context of a diffusion model, is a crucial technique for improving efficiency and performance. It allows the model to dynamically adjust its behavior by combining multiple expert models, each specialized for different stages of the denoising process. Instead of training many independent models, adaptive mixing leverages a smaller set of basis models and uses learnable coefficients to craft a much larger number of expert models on-demand. This strategy offers significant advantages over traditional multi-expert approaches. First, it reduces training costs dramatically by sharing weights across experts. Second, it enables adaptive allocation of model capacity across different timesteps, focusing more resources on challenging steps while efficiently handling easier ones. Third, it provides flexibility to generate a practically unlimited number of experts, which eliminates the need to pre-determine the ideal number of intervals in the denoising chain. Learnable mixing coefficients play a key role. They act as adaptive weights, learning to blend basis models in a way that optimizes the overall denoising performance. The effectiveness of adaptive mixing is demonstrated by its superior generation quality compared to independent multi-expert models while maintaining a low computational cost, indicating its significant potential for advancing the field of diffusion models.

Basis Model Fusion

#

Basis model fusion, in the context of the research paper, likely refers to a method of combining multiple, smaller diffusion models to create a more powerful and efficient model. Instead of training many large, independent models, this approach focuses on creating a set of ‘basis’ models and then using learnable mixing coefficients to linearly combine them. This is a significant advantage as it significantly reduces training costs and computational overhead compared to training numerous large models independently. The learnable coefficients are crucial, adapting the model’s capacity across different denoising timesteps and enabling an effective allocation of resources, ultimately improving the overall generation quality. This adaptive capacity allocation is a key strength, addressing challenges inherent in multi-expert denoising where a uniform distribution of capacity across intervals often leads to inefficiency. Further, the shared architecture with standard diffusion transformers ensures that the fused model maintains computational efficiency.

Efficiency Gains

#

Analyzing efficiency gains in a research paper requires a nuanced approach. We need to consider not only computational efficiency (e.g., reduced training time, lower memory footprint), but also sample efficiency (fewer samples needed to achieve a given performance level) and inference efficiency (faster generation of results). The paper likely explores how proposed techniques improve one or more of these efficiency metrics. Quantifying these gains is crucial, ideally through rigorous experimentation and comparison to state-of-the-art baselines. Furthermore, the analysis should discuss the trade-offs between efficiency and performance. For instance, a method that achieves significant efficiency improvements may sacrifice some output quality, which would need to be weighed carefully. It is also important to consider the potential for scalability. A highly efficient method for small-scale tasks may not be as efficient when scaled to larger datasets or models. Finally, a thorough analysis should delve into the underlying reasons for any observed efficiency improvements, explaining how the method’s design and architecture contribute to faster training, lower memory consumption or faster inference.

Future Directions

#

Future research could explore several promising avenues. Improving the efficiency of training multiple expert models is crucial; current methods are computationally expensive. Investigating alternative training strategies, such as hierarchical training or knowledge distillation, could significantly reduce this overhead. Exploring different mixing strategies beyond linear combinations could lead to more nuanced and effective expert fusion. This includes exploring non-linear mixing functions or attention mechanisms to adaptively weigh the contribution of each expert. Applying Remix-DiT to other generative models beyond diffusion models, such as GANs or VAEs, warrants investigation to assess its broader applicability and effectiveness. Finally, a comprehensive study analyzing the learned mixing coefficients and their relationship to the characteristics of the denoising process at various timesteps could reveal valuable insights into the underlying mechanisms of Remix-DiT and guide further improvements.

More visual insights

#

More on figures

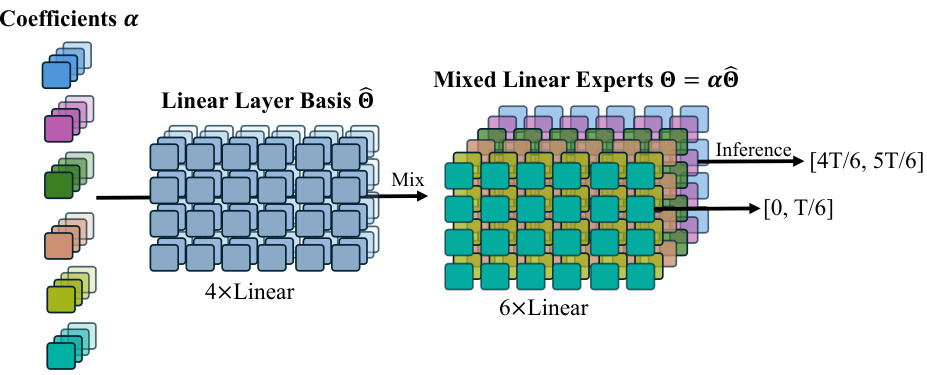
This figure illustrates the core concept of Remix-DiT, which uses a learnable mixing mechanism to create multiple expert models from a smaller set of basis models. The figure shows how 4 linear layer basis models are mixed using learnable coefficients α to produce 6 expert layers. Each expert layer is a weighted combination of the basis layers. This allows for efficient creation of many experts without the computational cost of training each independently. The experts are activated one at a time during inference and training, leading to cost efficiency.

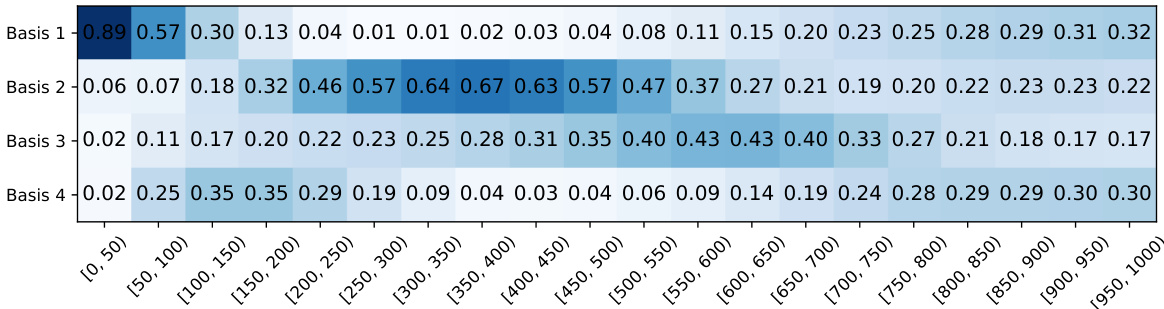
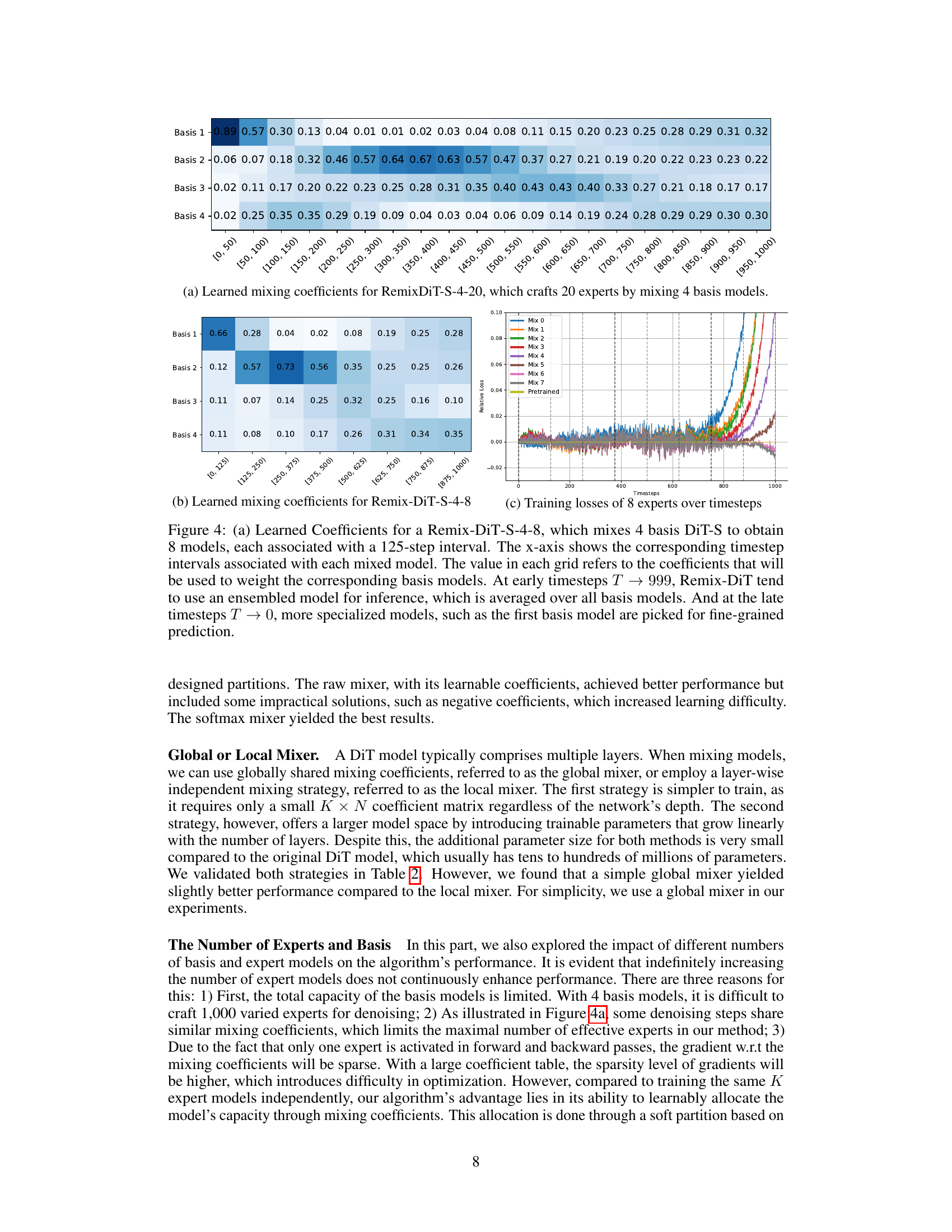
Figure 4 visualizes the learned mixing coefficients and training losses for Remix-DiT models with different numbers of experts and basis models. Panel (a) shows the coefficients for a model creating 20 experts from 4 basis models, illustrating how the coefficients change across different timesteps (denoising stages). Panel (b) shows the same visualization for a model with 8 experts and 4 basis models. Finally, panel (c) displays the training loss curves for each of the 8 experts, highlighting their specialized performance at different timesteps within their assigned intervals.

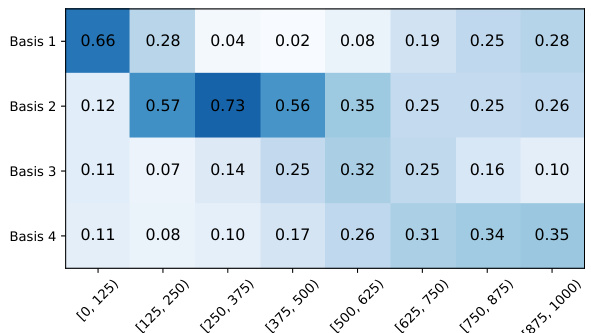
Figure 4 visualizes the learned mixing coefficients and training losses for Remix-DiT models with different numbers of experts and basis models. Subfigure (a) shows the coefficients used to mix 4 basis models into 20 experts for Remix-DiT-S-4-20. It highlights how the model weights the basis models differently across various timesteps, showing a preference for specific basis models at certain noise levels. Subfigure (b) shows similar results but with 8 experts instead of 20, using the same 4 basis models. Subfigure (c) presents the training losses for each of the 8 experts across the timesteps, illustrating the specialization achieved by the model; each expert tends to have lower loss within its assigned timestep interval.

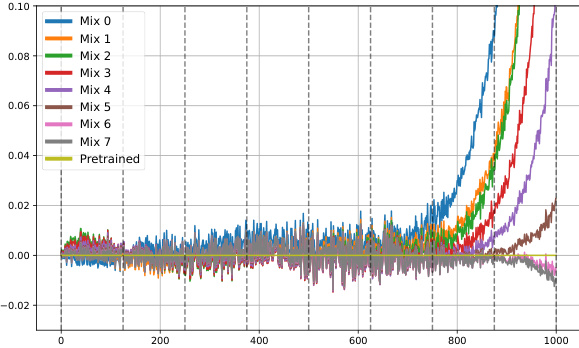
Figure 4 visualizes the learned mixing coefficients and training losses for Remix-DiT models with different numbers of experts and basis models. (a) shows the coefficients used to mix 4 basis models to create 20 experts, revealing how the model allocates capacity across different timesteps. (b) displays similar information but for 8 experts and 4 basis models. Finally, (c) plots the training losses for each of the 8 experts over 1000 timesteps, showing the specialization of experts across different time intervals.

This figure displays a comparison of image generation results between the standard DiT-B model and the proposed Remix-DiT-B model. Five example images are shown for each model, illustrating the differences in image quality and detail produced by the two approaches. Remix-DiT-B aims to improve image quality by using a novel multi-expert denoising method. The visual comparison allows for a qualitative assessment of the effectiveness of the Remix-DiT approach in enhancing image generation.

More on tables

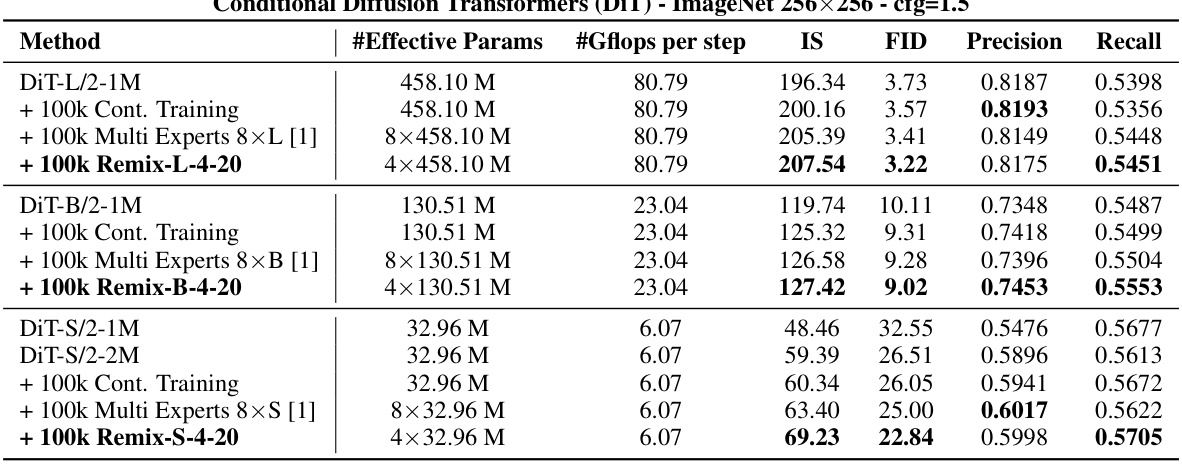
This table presents the results of fine-tuning standard DiT models using the Remix-DiT approach. It compares the performance of different models on ImageNet-256x256 after 100k fine-tuning steps. The models compared include standard DiTs, DiTs with continued training, multi-expert DiTs, and Remix-DiTs. The metrics used for comparison include Inception Score (IS), Fréchet Inception Distance (FID), Precision, and Recall. The table highlights that Remix-DiT achieves superior performance compared to other methods while maintaining a similar architecture and computational efficiency.

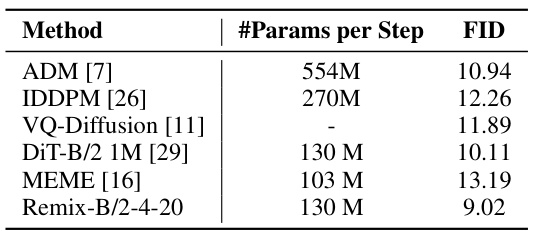
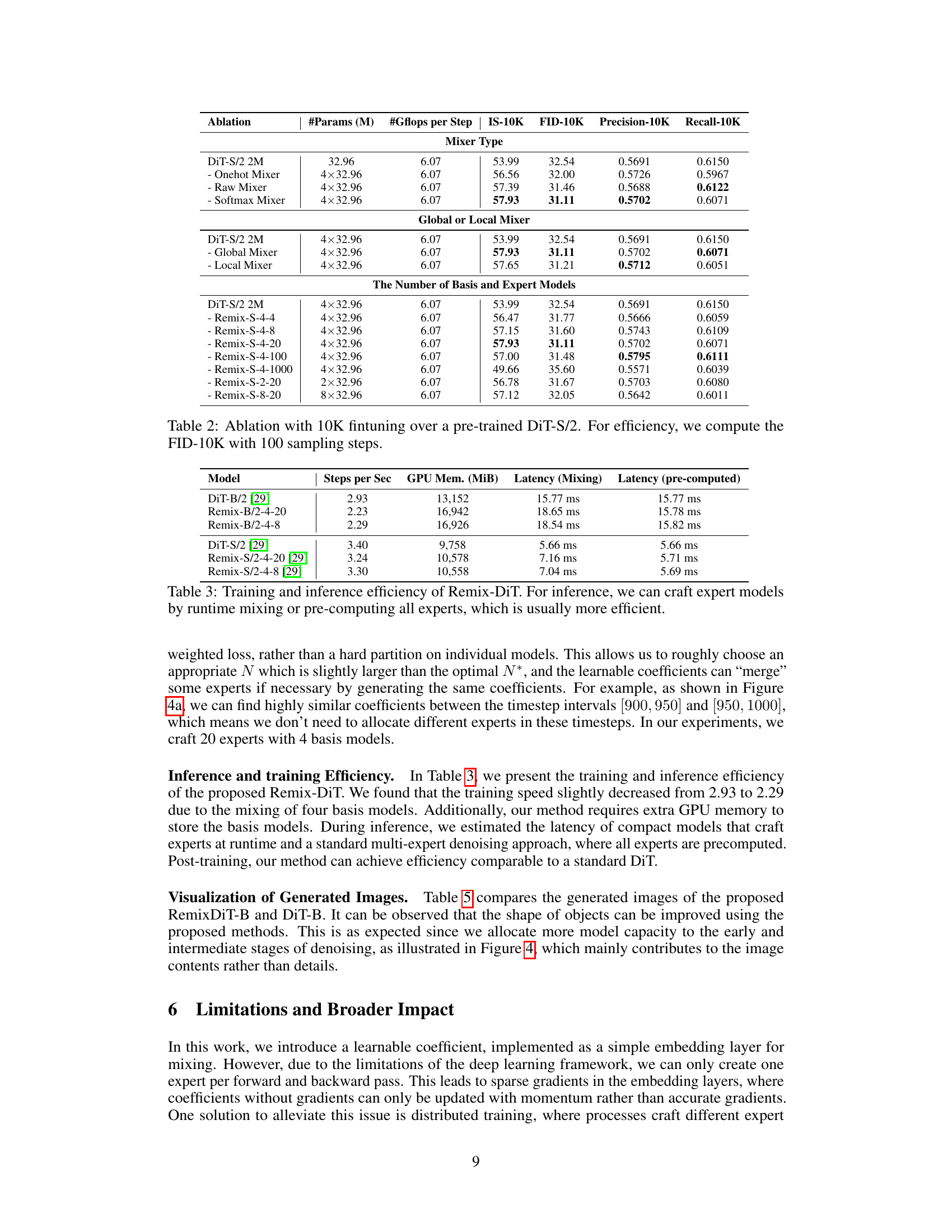
This table compares the performance of Remix-DiT with other state-of-the-art diffusion models on the ImageNet dataset. The comparison is based on the FID (Fréchet Inception Distance) score, a metric that measures the quality of generated images. The table shows that Remix-DiT achieves a FID score of 9.02, which is lower than the FID scores of other methods, indicating that Remix-DiT generates higher quality images.

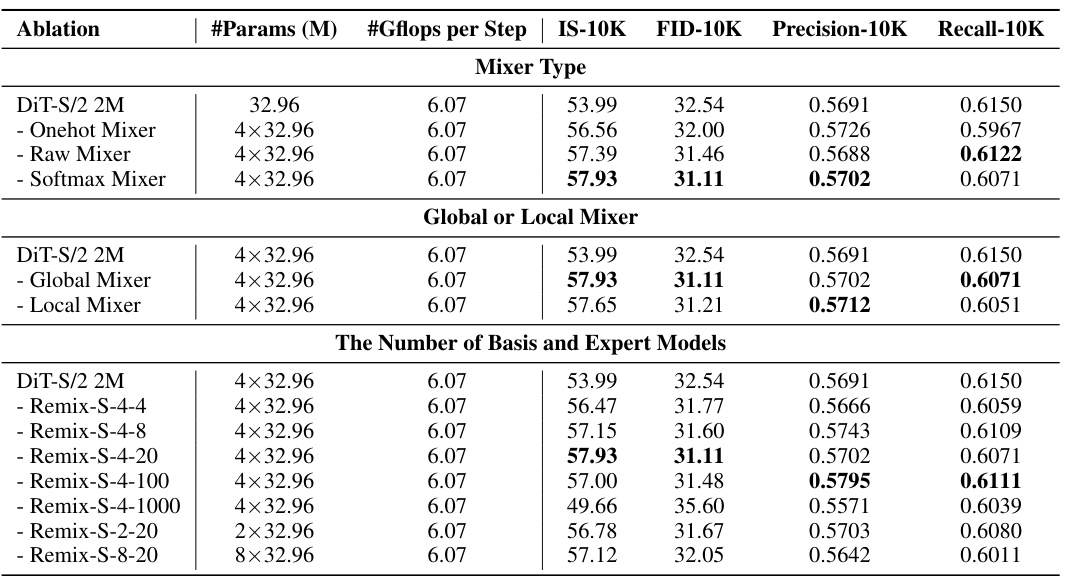
This table shows the results of fine-tuning pre-trained Diffusion Transformers (DiT) models for 100,000 steps on the ImageNet-256x256 dataset. It compares the performance of several models: the standard DiT models, continual training on the standard DiT, multi-expert models, and the proposed Remix-DiT models. The evaluation metrics used are Inception Score (IS), Fréchet Inception Distance (FID), Precision, and Recall. The key takeaway is that Remix-DiT achieves competitive or better results with fewer parameters than the other methods. Note that during inference, all expert models in Remix-DiT share the same architecture as a standard DiT, making the inference process efficient.

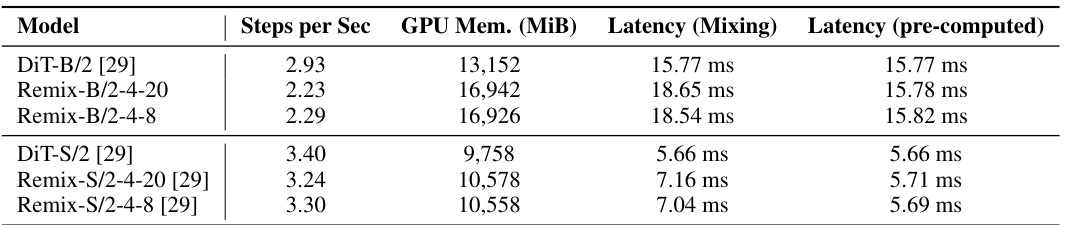
This table presents a comparison of the training and inference efficiency between the standard DiT model and the proposed Remix-DiT model. The metrics shown are steps per second, GPU memory usage (in MiB), latency for runtime mixing, and latency when experts are pre-computed. The results show a trade-off between training speed and memory usage, with pre-computed experts offering faster inference.

Full paper

#