↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Dynamic graph link prediction is a challenging task due to the complexity of modeling both spatial and temporal dependencies. Existing methods often suffer from limitations such as oversquashing and under-reaching, especially when using fully-connected Graph Transformers (GT). These methods often fail to capture essential spatio-temporal information in the graph’s structure and dynamics. This paper introduces SLATE, a novel approach that addresses these limitations.
SLATE leverages the spectral properties of a supra-Laplacian matrix to represent the dynamic graph as a multi-layer structure. This unique representation allows for a unified spatio-temporal encoding that captures both spatial and temporal information effectively. Furthermore, SLATE incorporates a cross-attention mechanism to model pairwise relationships between nodes, providing an accurate representation of dynamic edges. The experimental results show that SLATE significantly outperforms existing methods on several benchmark datasets, demonstrating its superior performance and scalability.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in dynamic graph analysis and link prediction. It introduces a novel spatio-temporal encoding method that significantly improves the accuracy and efficiency of transformer models on dynamic graphs. This work opens new avenues for research, particularly in areas with limited prior work. The superior performance and scalability demonstrated in the experiments make it highly relevant to current research trends in graph neural networks and data analysis.
Visual Insights#
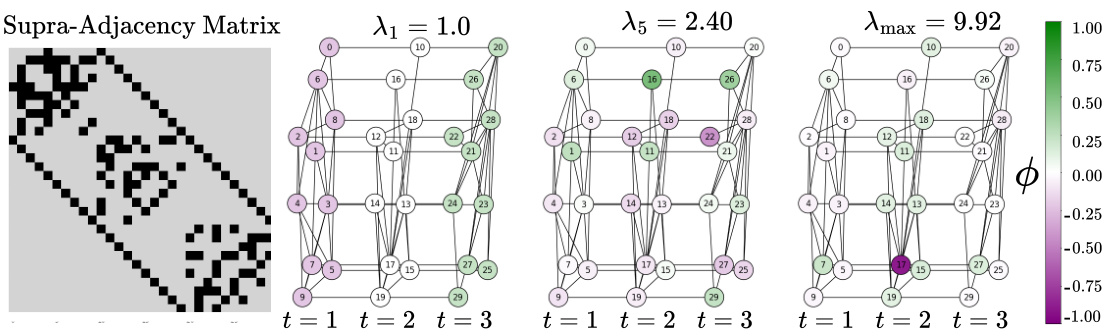
This figure illustrates the core concept of SLATE, showing how it represents a Discrete Time Dynamic Graph (DTDG) as a multilayer graph to capture both spatial and temporal information. The left panel displays the supra-adjacency matrix of a sample DTDG. The right panel shows the eigenvalues and eigenvectors of the supra-Laplacian matrix, demonstrating how the eigenvectors associated with smaller eigenvalues capture global dynamics, while those associated with larger eigenvalues capture more localized dynamics.
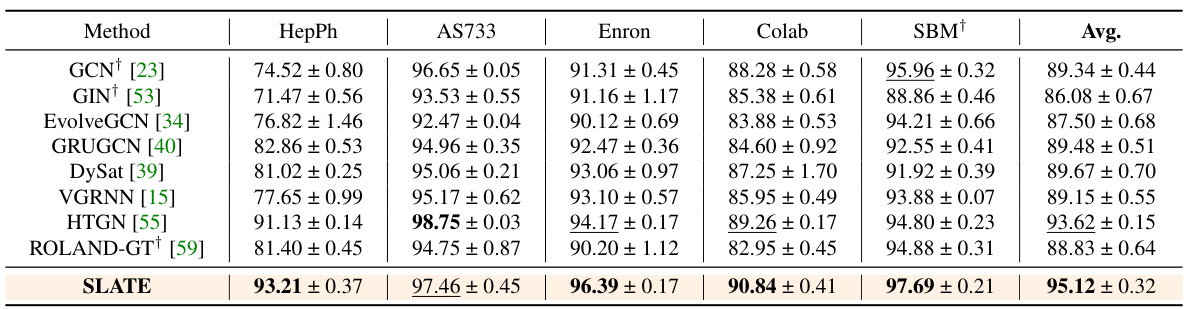
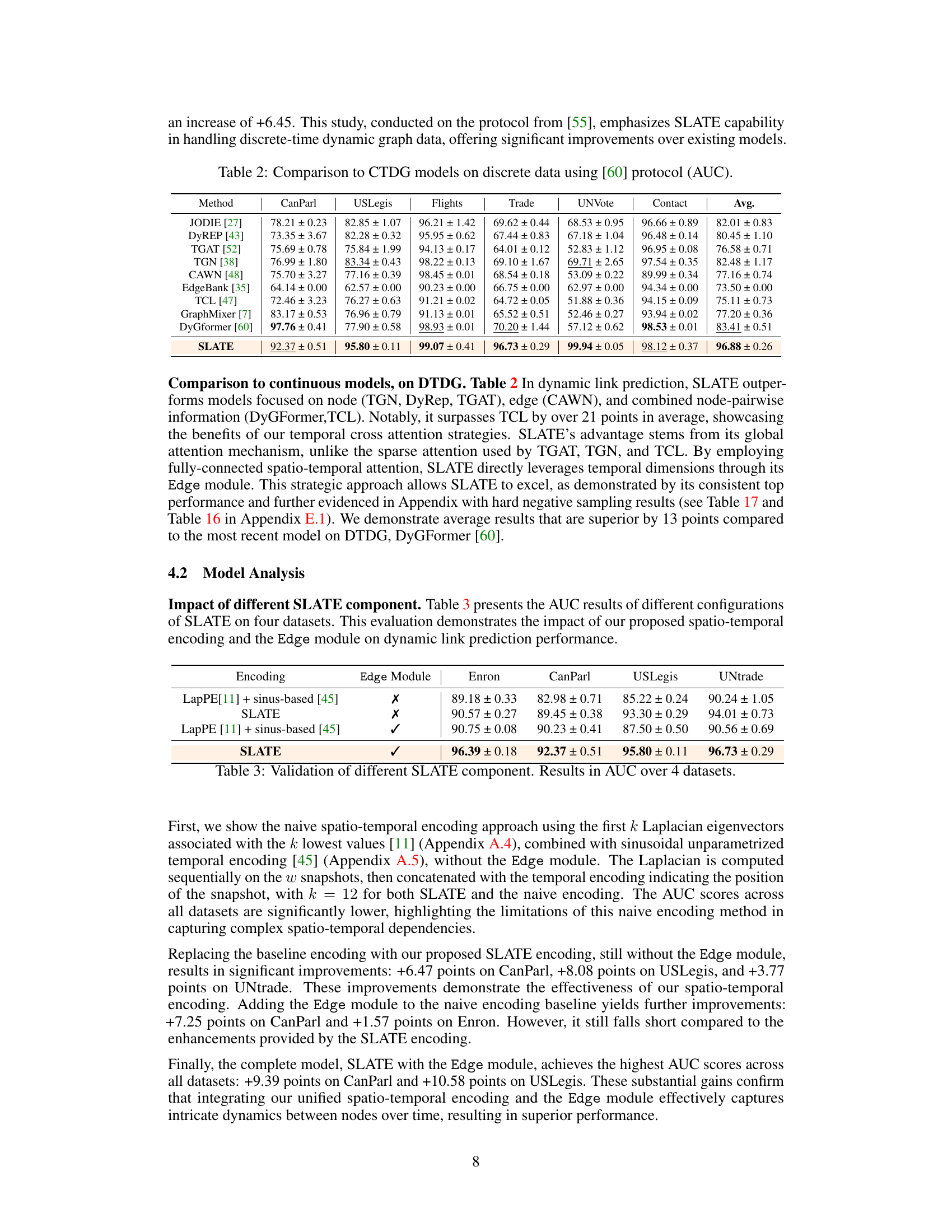
This table compares the performance of the proposed SLATE model against several state-of-the-art Dynamic Time Dynamic Graph (DTDG) models on 11 real and synthetic datasets. The comparison focuses on the ROC-AUC metric, providing a quantitative assessment of each model’s ability to accurately predict links in dynamic graphs. The results highlight SLATE’s superior performance across various datasets.
In-depth insights#
Supra-Laplacian Power#
The concept of “Supra-Laplacian Power” is intriguing and suggests a potential extension of spectral graph theory to the analysis of dynamic graphs. A supra-adjacency matrix, representing the temporal evolution of a graph across multiple snapshots, can be constructed. From this, a supra-Laplacian matrix is derived and its eigenvalues and eigenvectors analyzed. The “power” likely refers to the use of these spectral properties, perhaps through matrix exponentiation or similar transformations, to enrich node embeddings and edge representations. This could leverage higher-order information not easily captured by traditional methods, potentially improving the performance of graph neural networks (GNNs) or graph transformers on dynamic graph tasks. A key challenge would lie in efficiently computing the power, as the computational cost can scale exponentially with the power. However, careful design might exploit the structure of the supra-Laplacian and the low-order eigenvectors to address this limitation. The exploration of this concept presents an opportunity to develop more expressive and informative representations for dynamic networks, crucial for time-series data in various domains.
Dynamic GT Encoding#
Dynamic Graph Transformer (GT) encoding aims to capture the temporal evolution of graph structures, a crucial aspect missing in traditional GTs designed for static graphs. Effective encoding must seamlessly integrate both spatial (graph structure) and temporal information, allowing the model to learn meaningful representations of evolving relationships. Challenges lie in how to efficiently represent the changing graph topology across multiple time steps while preserving the global context provided by the full graph. Approaches may involve designing specific temporal attention mechanisms that incorporate previous graph states or creating multi-layered representations to represent the graph evolution as a sequence of snapshots. A key design consideration is to avoid the computational burden associated with fully connected attention across all nodes and time steps, especially as the size of the graph and the number of timestamps increase. This calls for either sparse attention mechanisms or clever approximation techniques. Ultimately, a successful dynamic GT encoding should lead to improved performance in various downstream tasks, such as dynamic link prediction or node classification, by providing the model with richer and more informative contextualized representations.
Cross-Attention Edge#
The concept of “Cross-Attention Edge” suggests a novel approach to edge representation in graph neural networks, particularly within the context of dynamic graphs. Instead of relying solely on node features to define edge characteristics, this method leverages a cross-attention mechanism between the temporal representations of the nodes forming the edge. This allows the model to capture the evolving relationships between nodes over time, going beyond static representations and providing a more nuanced understanding of dynamic interactions. The cross-attention mechanism allows the model to attend to relevant temporal information from both nodes simultaneously, enriching edge representation. The efficiency and accuracy of link prediction are potentially enhanced because this approach directly addresses the temporal dynamics inherent in relationships. Furthermore, it offers improved scalability as it doesn’t require complex subgraph sampling or computationally expensive neighbor-matching techniques, typical in many existing dynamic link prediction models. The effectiveness of this approach rests upon the quality of node embeddings and how well the cross-attention mechanism captures intricate temporal dynamics specific to node interactions.
SLATE Scalability#
The section ‘SLATE Scalability’ in the research paper addresses the crucial aspect of computational efficiency and resource requirements for the proposed SLATE model. It acknowledges that the attention mechanism’s theoretical complexity scales quadratically with the number of nodes, posing a significant challenge for larger graphs. However, SLATE mitigates this issue through several key strategies: It leverages a single-layer transformer architecture, which has been shown to be highly effective for dynamic graph tasks, reducing computational overhead considerably. Furthermore, it employs techniques such as Flash Attention and Performer to optimize both memory consumption and computational time. Flash Attention significantly enhances efficiency in handling long sequences, while Performer enables linear time complexity for attention calculations. The paper substantiates these claims with experimental results, showcasing SLATE’s impressive performance on relatively large datasets, underscoring its scalability and practicality despite the inherent computational complexity of attention-based models. This scalability, achieved through architectural choices and algorithmic optimizations, is a key strength of the SLATE model.
Future Enhancements#
Future enhancements for this research could explore several promising avenues. Extending SLATE to handle very large graphs is crucial, perhaps through techniques like graph sampling or hierarchical attention mechanisms. Addressing the transductive nature of the model is another key area; incorporating inductive capabilities would greatly broaden its applicability. Investigating alternative spatio-temporal encoding schemes beyond the supra-Laplacian, potentially exploring techniques better suited for specific graph types or dynamic patterns, could yield further improvements. A more thorough analysis of the impact of different hyperparameters on model performance could lead to more robust and effective configurations. Finally, combining the strengths of SLATE’s global attention with those of message-passing GNNs, which excel at capturing local structure, in a hybrid architecture might unlock even better predictive performance. The successful incorporation of these enhancements would make SLATE a more powerful and widely applicable tool for dynamic link prediction.
More visual insights#
More on figures
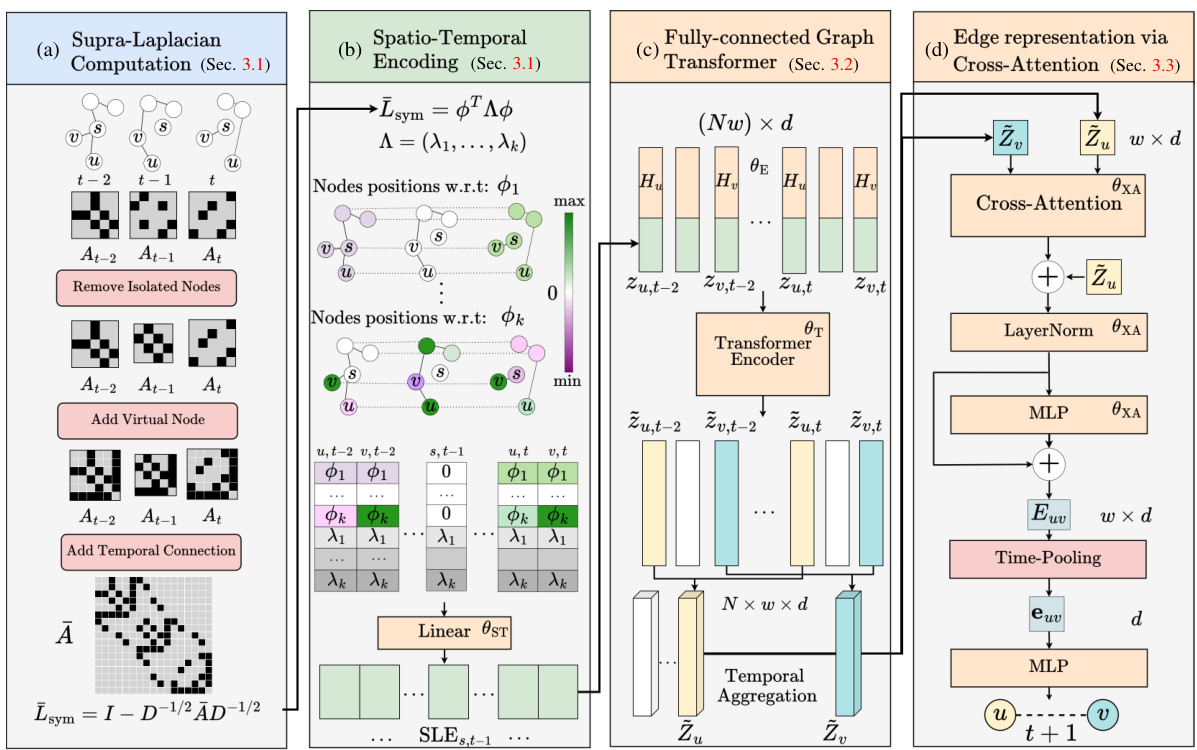
This figure illustrates the overall framework of the SLATE model. It shows how the model processes the input dynamic graph by adapting the supra-Laplacian matrix computation and performing spatio-temporal encoding to capture the spatio-temporal structure, using a fully-connected spatio-temporal transformer and an edge representation module using cross-attention for accurate link prediction.
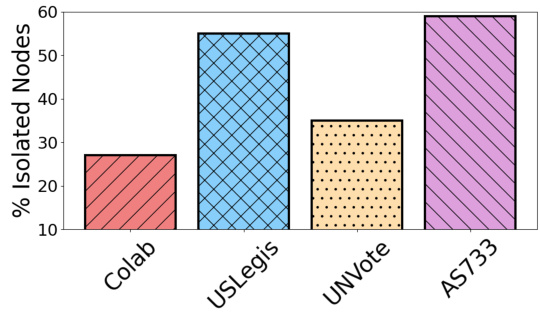
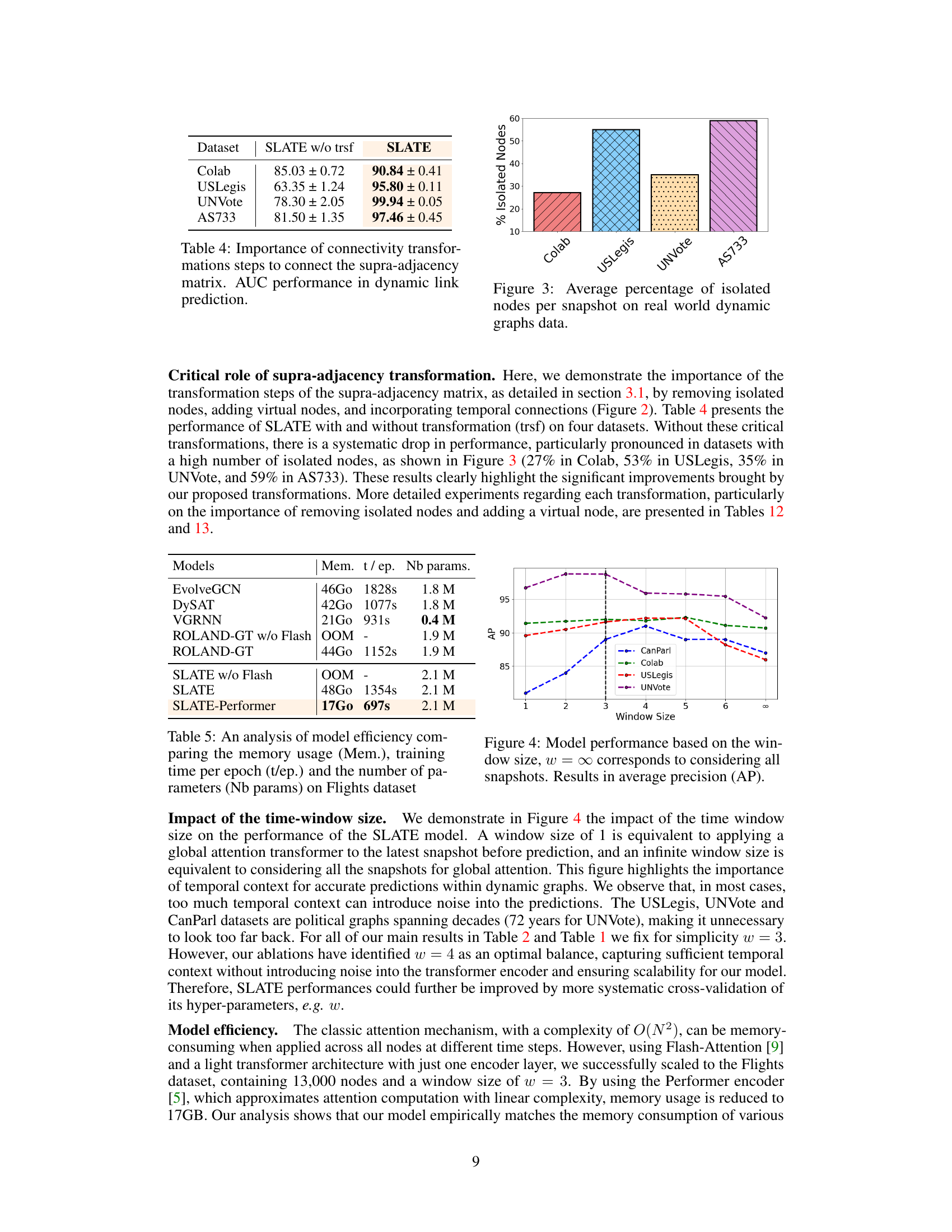
This figure shows the percentage of isolated nodes per snapshot across four real-world dynamic graph datasets: Colab, USLegis, UNVote, and AS733. It highlights the prevalence of isolated nodes, especially in datasets like USLegis and AS733, which have a high percentage of isolated nodes, making them challenging for conventional graph processing techniques. This observation underscores the need for the graph connection strategies employed by the SLATE model in handling isolated nodes before spectral analysis and multi-layer graph transformation. The significance of this is explained later in section 4.2.
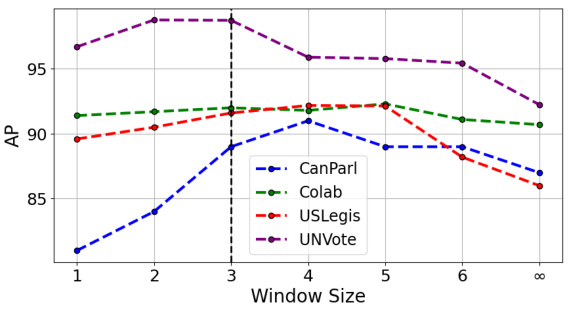
This figure shows the impact of the time window size on the performance of the SLATE model. A window size of 1 means only the latest snapshot is used for prediction, while a size of ∞ considers all snapshots. The results are shown as average precision (AP) across four datasets (CanParl, Colab, USLegis, UNVote). The figure demonstrates that an optimal window size exists for each dataset; using too much temporal context can introduce noise, while too little may miss important temporal dependencies.
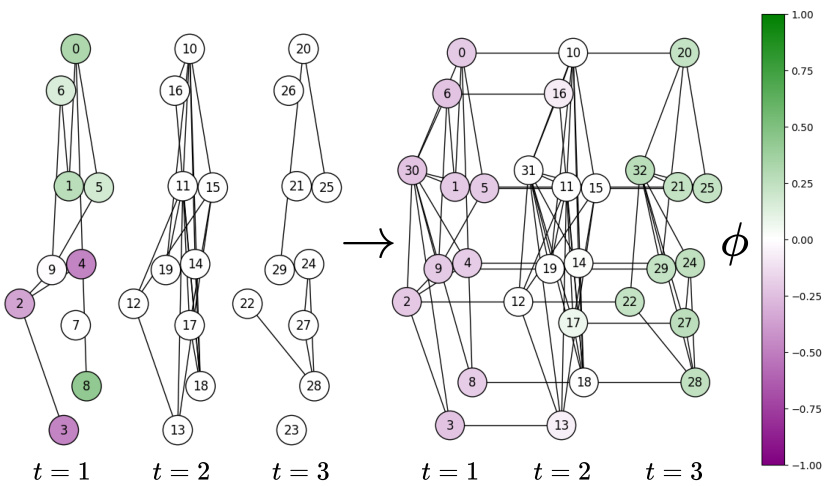
This figure illustrates the process of transforming a random Discrete Time Dynamic Graph (DTDG) into a connected multi-layer graph. The left side displays three independent snapshots of the DTDG, each containing isolated nodes and disconnected clusters. The right side shows the result of applying the transformations used in the SLATE method. This involves removing isolated nodes, adding temporal connections between nodes, and introducing a virtual node to connect the remaining clusters within each snapshot. The resulting graph is fully connected and captures both spatial and temporal information.
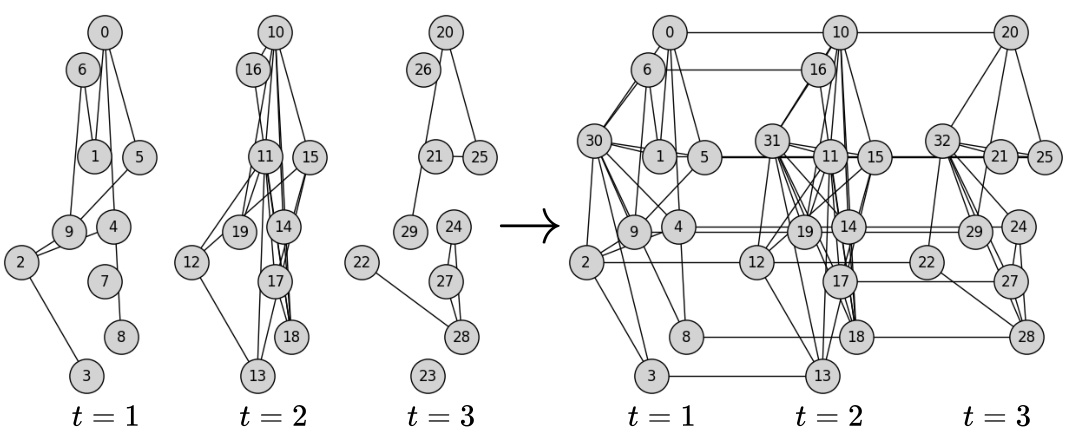
This figure illustrates the transformation of a discrete-time dynamic graph (DTDG) into a connected multi-layer graph, a crucial step in the SLATE method. The left shows three separate snapshots of the DTDG, each with isolated nodes and clusters. The right shows the result of applying three transformations: removing isolated nodes, adding temporal connections between nodes present in consecutive snapshots, and introducing a virtual node to connect remaining clusters in each snapshot. This process creates a connected multi-layer graph suitable for the spectral analysis and spatio-temporal encoding used in SLATE.
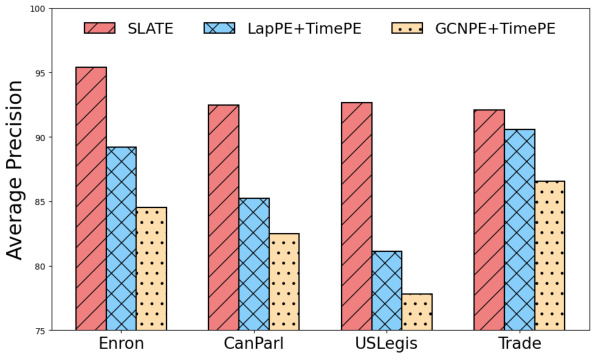
This figure compares the average precision achieved by three different encoding methods: SLATE’s unified spatio-temporal encoding, a separate Laplacian positional encoding combined with a sinusoidal temporal encoding, and a GCN positional encoding also combined with a sinusoidal temporal encoding. The results are shown for four different datasets (Enron, CanParl, USLegis, Trade), demonstrating SLATE’s superior performance compared to the other two methods which use separate encodings for spatial and temporal aspects of the data.

This figure illustrates the core concept of SLATE, which models a dynamic graph as a multi-layer graph and uses its supra-Laplacian matrix for spatio-temporal encoding. The left panel shows the construction of the supra-adjacency matrix, and the right panel shows its spectral analysis. The eigenvectors associated with smaller eigenvalues capture global dynamics, while those associated with larger eigenvalues capture localized spatio-temporal information.
This figure illustrates the SLATE model’s architecture. The left side shows the construction of the supra-adjacency matrix for a toy dynamic graph with three snapshots. The right side displays the spectrum analysis of the supra-Laplacian matrix. Eigenvectors associated with smaller eigenvalues capture global graph dynamics, while those associated with larger eigenvalues capture localized dynamics.
More on tables
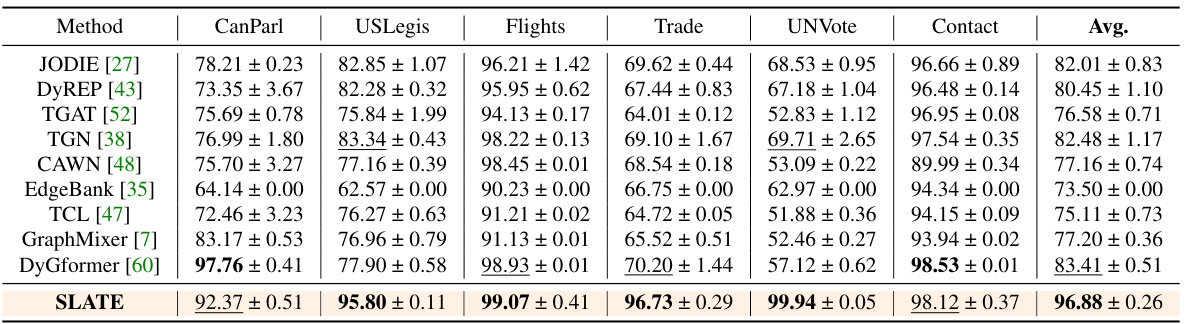
This table compares the performance of the proposed SLATE model against several state-of-the-art Dynamic Time Dynamic Graph (DTDG) models on discrete-time datasets. The comparison uses the ROC-AUC metric to evaluate link prediction accuracy. The table includes results across multiple datasets, illustrating the model’s performance across various graph structures and characteristics.

This table presents the AUC results of different configurations of SLATE on four datasets. It shows the impact of the proposed spatio-temporal encoding and the Edge module on dynamic link prediction performance. The rows represent different combinations of encoding (Laplacian positional encoding plus sinus-based temporal encoding vs. the proposed SLATE encoding) and the edge module (included or excluded). The columns represent the four datasets tested (Enron, CanParl, USLegis, UNtrade). The numbers are the AUC scores with standard deviations.
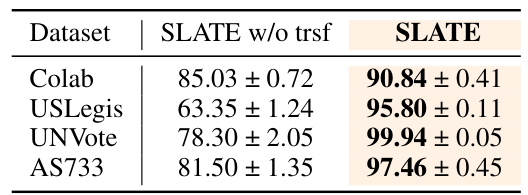
This table shows the AUC performance of SLATE with and without the three transformation steps (removing isolated nodes, adding virtual nodes, and adding temporal connections) on four different datasets. The results demonstrate the importance of these transformations in improving the model’s performance, particularly on datasets with a high number of isolated nodes.
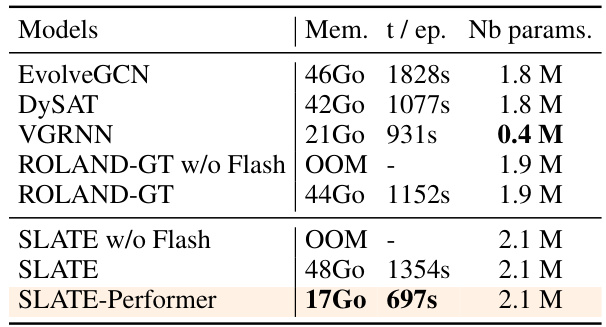
This table compares the memory usage, training time per epoch, and the number of parameters for different models on the Flights dataset. It highlights the efficiency gains achieved by using the Performer technique in the SLATE model, showing a significant reduction in memory usage and training time compared to other models while maintaining a similar number of parameters.

This table compares the performance of the proposed SLATE model against other state-of-the-art Dynamic Time Dynamic Graph (DTDG) models on several benchmark datasets. The comparison is based on the ROC-AUC metric, a common evaluation measure for link prediction tasks. The table shows SLATE consistently outperforms other methods across various datasets.
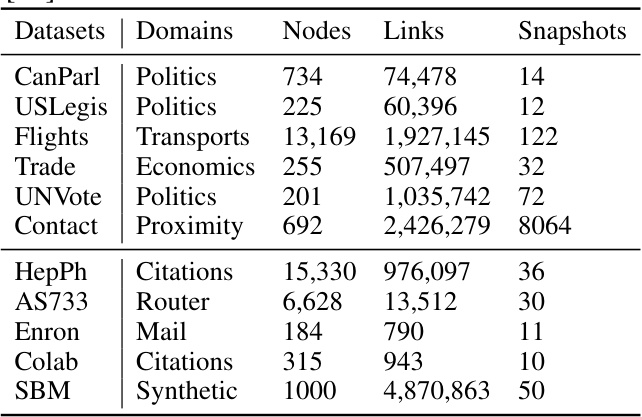
This table presents the characteristics of the eleven datasets used in the paper’s experiments. For each dataset, it lists the domain it represents (e.g., Politics, Transports, Citations), the number of nodes, the number of links, and the number of snapshots (time steps) available. The datasets are split into two groups, with a horizontal line separating those obtained from [60] and those from [55], indicating the source publications.

This table presents the comparison results of the proposed SLATE model against several state-of-the-art Dynamic Time Dynamic Graph (DTDG) models for link prediction on four discrete datasets (HepPh, AS733, Enron, Colab). The metrics used for comparison are ROC-AUC, Precision, Recall and F1-Score. The results show that SLATE significantly outperforms other methods across all metrics and datasets.
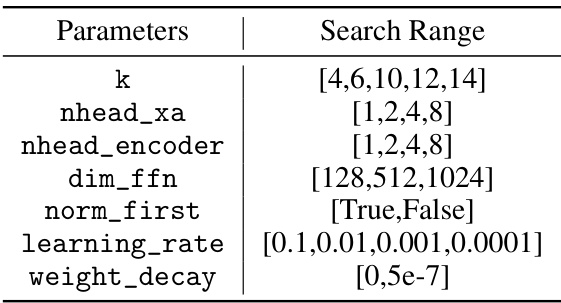
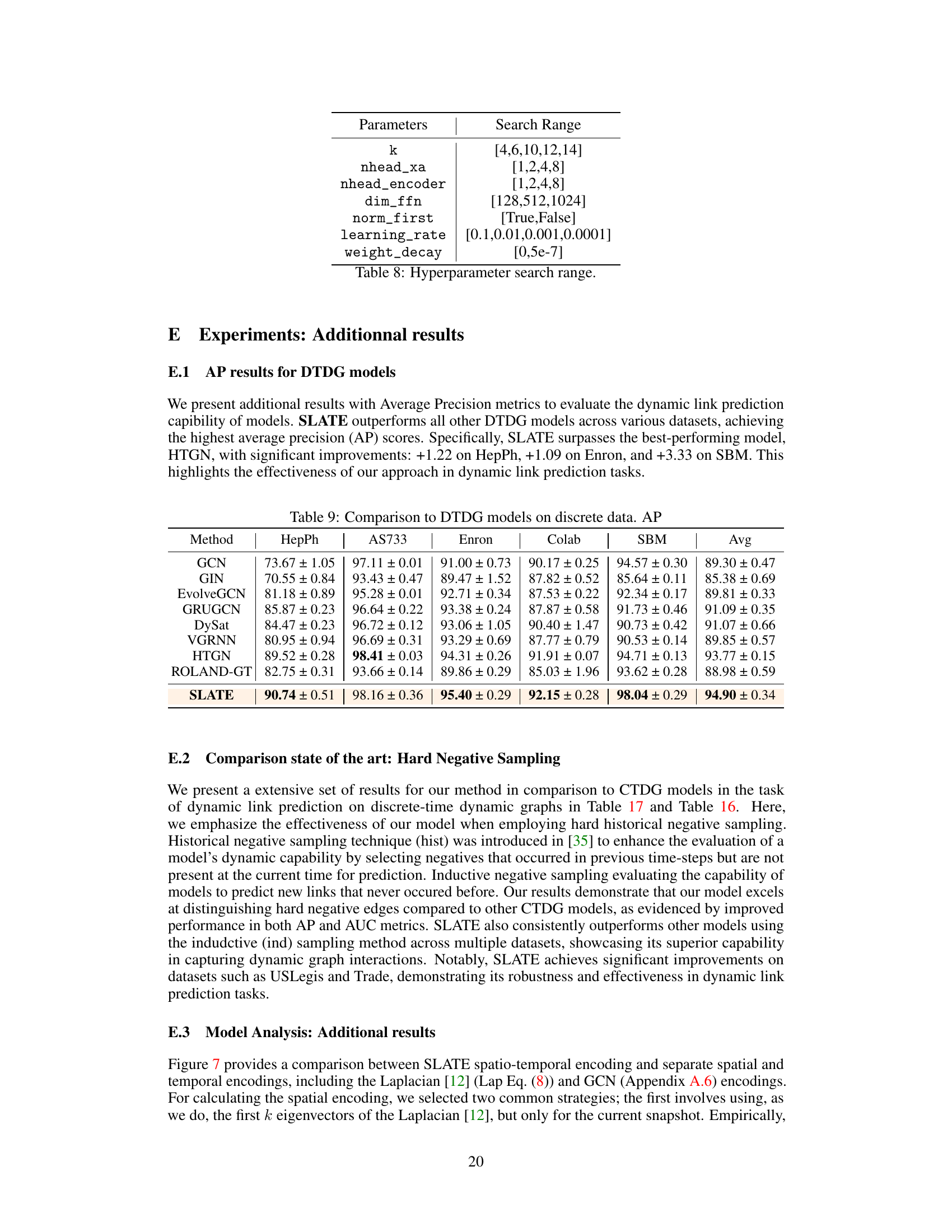
This table presents the hyperparameters used in the experiments and their corresponding search ranges. The hyperparameters include the number of eigenvectors (k), the number of attention heads in the cross-attention module and transformer encoder (nhead_xa, nhead_encoder), the dimension of the feed-forward network (dim_ffn), whether layer normalization is applied before the full attention (norm_first), the learning rate, and the weight decay. The search ranges indicate the values explored during hyperparameter tuning.
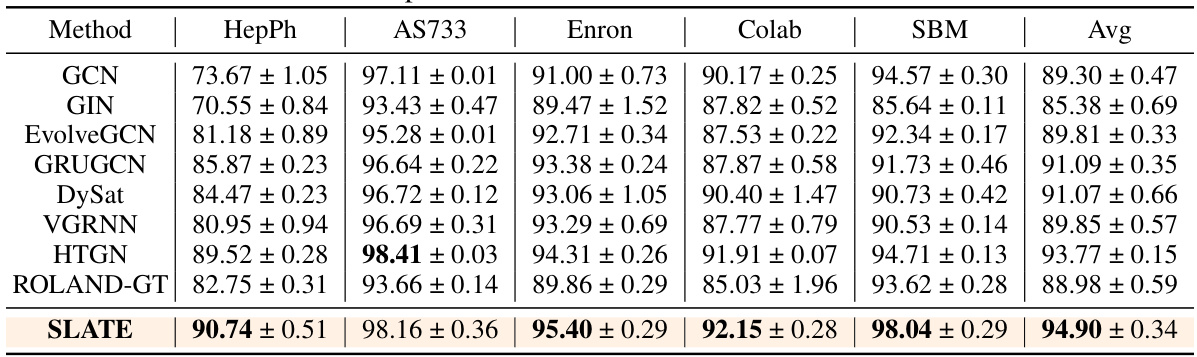
This table compares the performance of the proposed SLATE model against several state-of-the-art Dynamic Time Dynamic Graph (DTDG) models on discrete-time datasets. The comparison uses the ROC-AUC metric to evaluate the performance of each model in link prediction tasks. The table highlights SLATE’s superior performance across various datasets, often exceeding other methods by a significant margin.
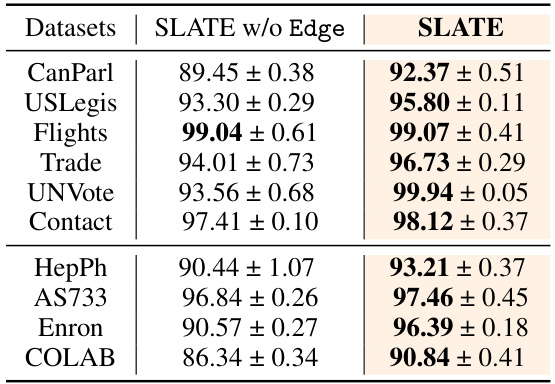
This table presents the Area Under the ROC Curve (AUC) scores for dynamic link prediction, comparing the performance of SLATE with and without the edge representation module. It showcases the improvement in AUC achieved by incorporating the edge module across various datasets. The results demonstrate the importance of the edge module for accurately capturing pairwise relationships and improving link prediction performance.
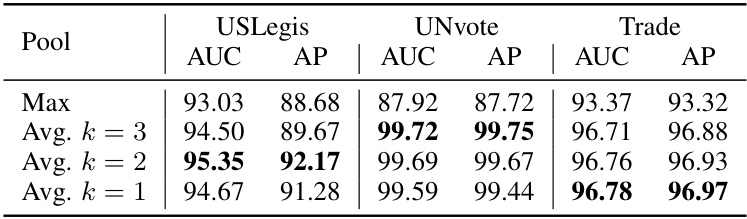
This table compares the performance of SLATE’s time pooling methods (Max, Avg k=3, Avg k=2, Avg k=1) across three datasets (USLegis, UNVote, Trade). It shows the Area Under the ROC Curve (AUC) and Average Precision (AP) for each method on each dataset. The results indicate the impact of the pooling method on the final prediction scores. In particular, it demonstrates the benefit of using averaging over max pooling.

This table compares the Area Under the Curve (AUC) scores for link prediction on the Colab and USLegis datasets using two different versions of the SLATE model. The first version retains isolated nodes, while the second removes them and focuses only on the eigenvectors associated with the first non-zero eigenvalue of the supra-Laplacian matrix. The results show a significant improvement in AUC when isolated nodes are removed, highlighting the importance of this preprocessing step for improving model performance.
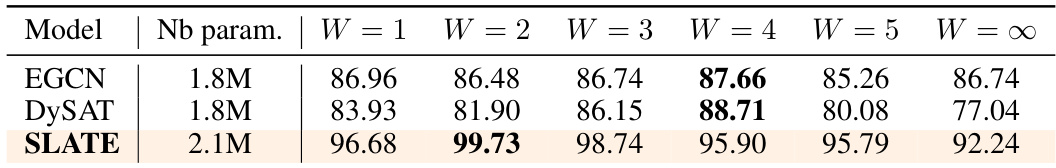
This table presents the performance of three different models (EGCN, DySAT, and SLATE) on the UNVote dataset for different time window sizes (from 1 to infinity). The results are expressed in terms of AUC. The table shows that smaller time windows tend to produce optimal results. Specifically, the best performance for EGCN and DySAT is obtained with a time window of 4, while SLATE performs best with a window of 2.

This table compares the Area Under the ROC Curve (AUC) performance of two variations of the SLATE model: one using a standard Transformer encoder and the other using a Performer encoder. The comparison is made across three datasets: AS733, USLegis, and UNtrade. The results show the impact of using the Performer encoder on the model’s performance.
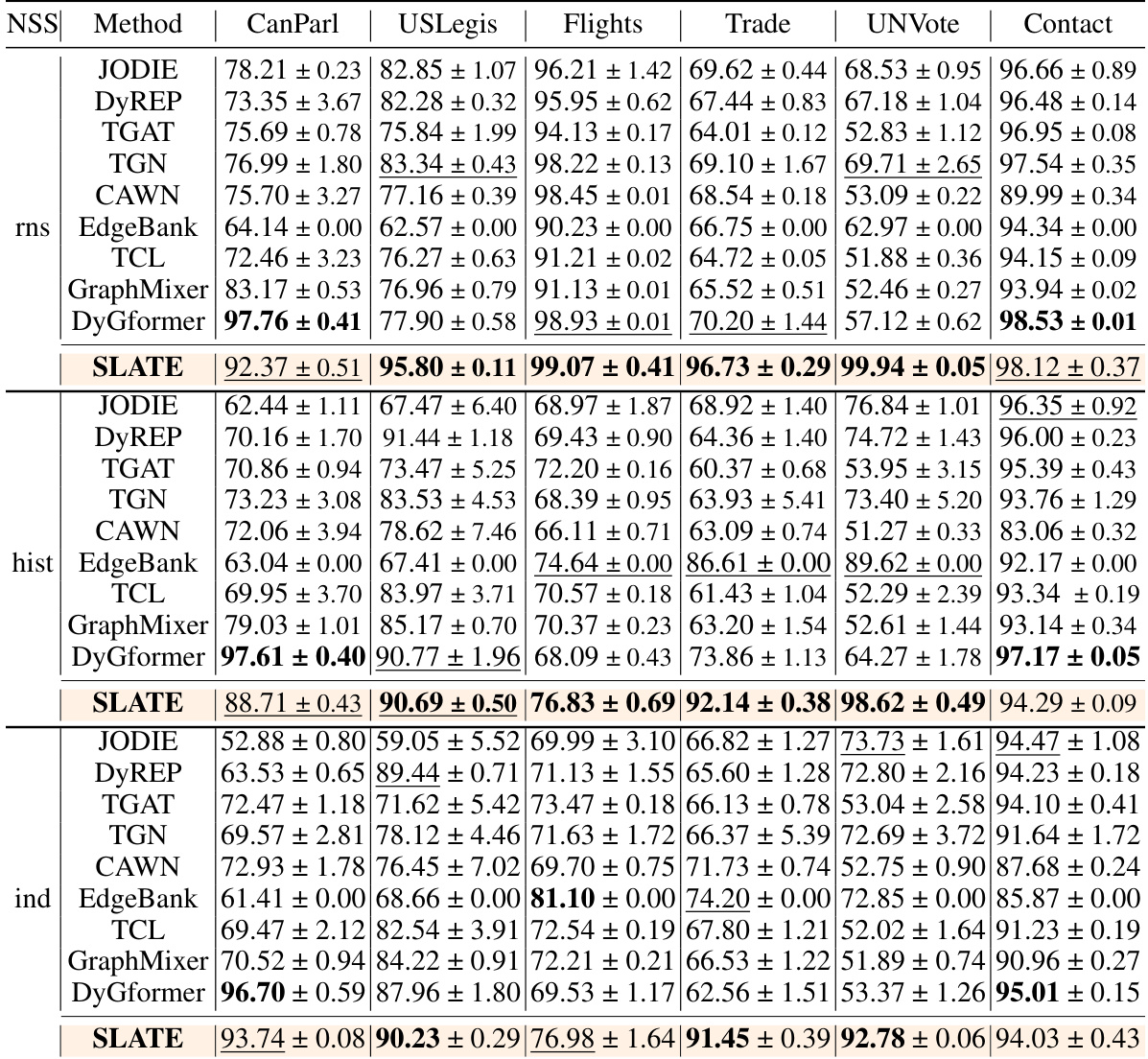
This table compares the performance of the proposed SLATE model against several state-of-the-art Dynamic Time Dynamic Graph (DTDG) models on eleven real and synthetic discrete-time dynamic graph datasets. The comparison uses the ROC-AUC metric, a standard measure for evaluating the performance of link prediction models. The results show that SLATE significantly outperforms existing methods across various datasets.

This table compares the performance of the proposed SLATE model against several state-of-the-art Dynamic Time Dynamic Graph (DTDG) models on various discrete-time datasets. The comparison uses the ROC-AUC metric to evaluate the link prediction accuracy of each model. The table highlights the superior performance of SLATE across multiple datasets.
Full paper#