↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Continual learning with Graph Neural Networks (GNNs) faces the challenge of catastrophic forgetting, where learning new tasks causes the model to forget previously learned information. Existing solutions often fall short by failing to adequately preserve the essential topological structures of the graph data, leading to inaccurate results. This often results in low performance when revisiting previous tasks.
The researchers introduce TACO, a topology-aware graph coarsening framework. TACO addresses this issue by using a novel graph coarsening algorithm called RePro. RePro efficiently reduces the size of the graph while preserving key topological features. By storing and replaying this reduced graph, TACO successfully mitigates catastrophic forgetting and significantly improves performance. The experimental results demonstrate that TACO outperforms existing methods on multiple benchmark datasets, highlighting the importance of preserving topological information in continual graph learning.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on continual learning and graph neural networks. It directly addresses the critical issue of catastrophic forgetting in GNNs, offering a novel framework and algorithm that significantly improve performance on streaming graph data. The proposed methods are highly efficient, adaptable, and relevant to various real-world applications involving dynamic graph data.
Visual Insights#

This figure shows two subfigures. (a) shows the distribution of classes in the Kindle dataset across five different time periods (tasks). It highlights that the class distribution shifts over time, with some classes becoming more prevalent and others less so. (b) displays the F1 score (a measure of classification accuracy) obtained by a model on each of the five tasks. Importantly, it demonstrates that a model trained on later tasks tends to perform poorly on the earlier ones, a phenomenon known as catastrophic forgetting.

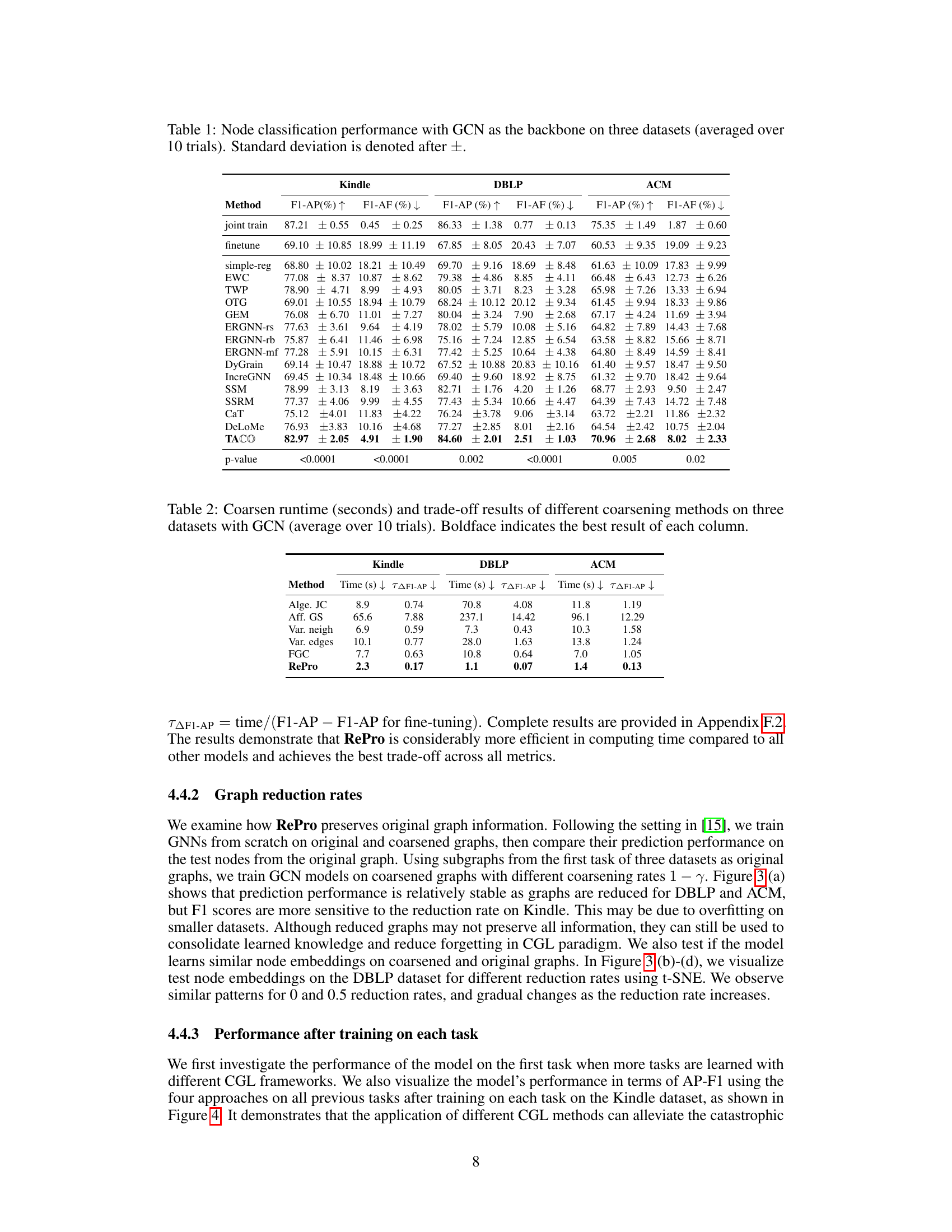
This table presents the results of node classification experiments using Graph Convolutional Networks (GCNs) as the backbone model on three different datasets. The table compares the performance of various continual learning methods, including the proposed TACO framework. The metrics used are Average Performance (AP) and Average Forgetting (AF) for macro F1 and balanced accuracy scores (BACC). The results are averaged over ten trials, and the standard deviations are provided.
In-depth insights#
Continual GNNs#
Continual learning in Graph Neural Networks (GNNs) presents unique challenges due to the complex structural nature of graph data. Catastrophic forgetting, where previously learned knowledge is lost when learning new tasks, is a significant hurdle. Existing approaches often fail to adequately address this issue, particularly when dealing with streaming graph data where the graph structure itself evolves over time. Methods that leverage experience replay show promise, but effectively preserving crucial topological information during the replay process is critical and often overlooked. Topology-aware graph coarsening techniques offer a potential solution, allowing for efficient storage of past experiences while preserving essential structural properties. Efficient coarsening algorithms, such as those that leverage node representation proximities, are key to the success of these approaches. Future research should focus on robust methods for handling the dynamics of real-world streaming graphs and developing more sophisticated mechanisms to minimize catastrophic forgetting while maintaining efficiency. The development of techniques that effectively balance topological preservation with computational efficiency remains a key challenge.**
TACO Framework#
The TACO framework, a topology-aware graph coarsening approach for continual graph learning, tackles the catastrophic forgetting problem in Graph Neural Networks (GNNs). It cleverly combines new and old graph data, efficiently preserving crucial topological information through a coarsening process. The framework’s main strength lies in its ability to accurately capture and replay past experiences without significant information loss, unlike many other methods that fail to retain the essential structural properties of graphs. The key innovation within TACO is the integration of a novel graph coarsening algorithm, RePro, which reduces graph size by merging similar nodes based on their representation proximities, thereby maintaining structural integrity. This method addresses the limitation of existing graph reduction techniques that often overlook node features. Furthermore, TACO incorporates a node fidelity preservation strategy to safeguard against the loss of minority classes during coarsening, ensuring balanced representation across all classes. This multifaceted approach provides a robust and scalable solution for continual learning on streaming graphs.
RePro Algorithm#
The RePro algorithm, a core component of the TACO framework, is a novel graph coarsening method designed for continual graph learning. It leverages node representation proximities to efficiently reduce graph size while preserving crucial topological information. Unlike traditional methods focused solely on spectral properties or graph structure, RePro considers feature similarity, neighbor similarity, and geometric closeness to determine node similarity. This multi-faceted approach leads to more effective merging of nodes into super-nodes. A key innovation is Node Fidelity Preservation, a strategy to protect important nodes from being compressed, thus mitigating the loss of minority classes and maintaining high-quality topological information. The theoretical analysis of Node Fidelity Preservation provides a strong foundation for the algorithm’s efficacy in preserving essential information, demonstrating its superiority over existing coarsening methods. This algorithm is designed to be computationally efficient, offering a significant improvement in scalability for continual learning tasks. The use of pre-trained node embeddings eliminates the need for computationally expensive spectral similarity calculations, ensuring that the performance of graph coarsening is substantially improved.
Ablation Studies#
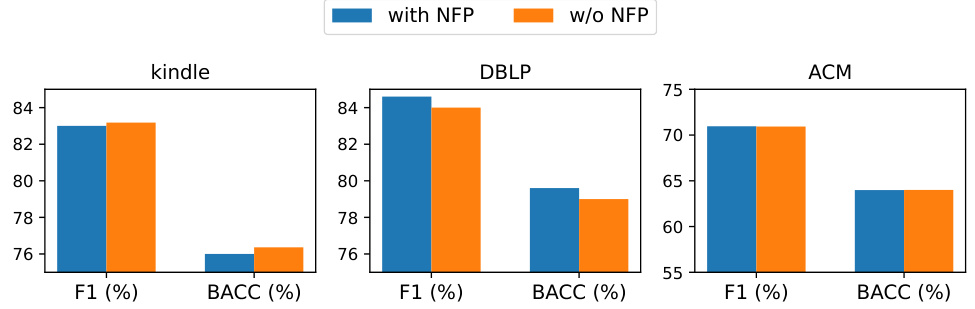
Ablation studies systematically remove components of a model or system to assess their individual contribution. In this context, it would involve removing parts of the proposed continual graph learning framework (e.g. the graph coarsening algorithm, the node fidelity preservation strategy, or specific memory buffer implementations) to isolate their effects on performance. By comparing the results with and without these components, the researchers could verify their claims about the necessity of each individual element for high performance. For example, removing the graph coarsening technique would reveal whether preserving high-quality topological information is crucial for performance, while disabling node fidelity preservation may highlight its importance in mitigating the decline of minority classes. The depth and thoroughness of these experiments will reveal how well-designed and robust the entire framework is. Overall, ablation studies are an important method to identify the core aspects responsible for successful continual graph learning in the model, paving the way for more efficient and reliable designs in the future.
Future Work#
Future research directions stemming from this topology-aware graph coarsening framework for continual graph learning could involve extending the framework to handle more complex graph structures, such as those with multiple relation types or dynamic node/edge attributes. Investigating the framework’s performance on diverse graph types and tasks is crucial. Exploring alternative graph reduction techniques beyond the proposed RePro method would enhance robustness. Furthermore, the impact of different node sampling strategies and the effectiveness of other node importance measures warrant deeper investigation. Finally, a comprehensive analysis of the trade-offs between accuracy, efficiency, and memory usage for various parameter settings would provide valuable insights for practical deployment and enhance generalizability.
More visual insights#
More on figures
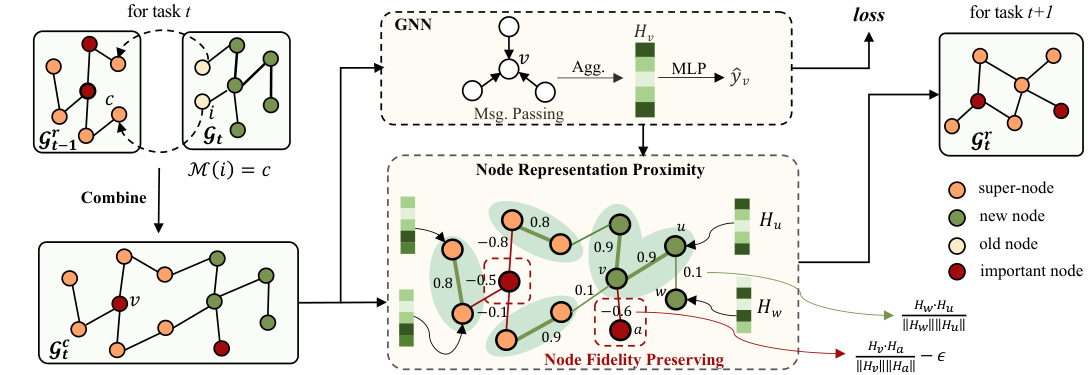
This figure illustrates the TACO framework’s workflow. It shows how, at each time step (t), the coarsened graph from the previous time step (Gt-1) is combined with the current time step’s original graph (Gt) to create a combined graph (Gε). Important nodes are selected and updated with new nodes, and the model is trained on this combined graph (Gε). Finally, Gε undergoes coarsening to produce the reduced graph (Gt) for the next time step.

This figure shows the results of experiments evaluating the impact of graph reduction rates on the performance of a Graph Convolutional Network (GCN) model for node classification. The first subplot (a) presents the test macro-F1 scores across three datasets (Kindle, DBLP, ACM) at varying reduction rates, demonstrating how coarsening affects performance. Subplots (b), (c), and (d) visualize the t-SNE embeddings of test nodes from the DBLP dataset after training on graphs coarsened with reduction rates of 0, 0.5, and 0.9, respectively. These visualizations illustrate how the node embeddings change with different reduction rates.

This figure shows two subfigures. Subfigure (a) presents the distribution of classes in the Kindle dataset across five different time periods (tasks). It visually demonstrates how the class distribution shifts over time. Subfigure (b) shows the F1 scores obtained by a Graph Convolutional Network (GCN) when trained sequentially on the different tasks. It illustrates the phenomenon of catastrophic forgetting, where the model’s performance on older tasks degrades as it learns new tasks. This highlights the problem of continual graph learning and motivates the need for improved methods that can preserve previously learned knowledge.

This figure shows the results of experiments evaluating the impact of graph reduction rates on the performance of a GCN model for node classification. Subfigure (a) presents a graph illustrating the relationship between reduction rate and macro-F1 score across three datasets (Kindle, DBLP, and ACM). Subfigures (b), (c), and (d) use t-SNE to visualize the node embeddings from the DBLP dataset for reduction rates of 0, 0.5, and 0.9 respectively. The visualizations help to assess how well the essential topological information is preserved during the graph coarsening process at different reduction rates.
This figure shows the results of experiments evaluating the impact of graph reduction rate on model performance and node embedding similarity. (a) plots the macro-F1 scores on test sets across three different datasets for various graph reduction ratios. (b)-(d) visualize the t-SNE embeddings of test nodes from the DBLP dataset, comparing embeddings for different reduction rates (0, 0.5, 0.9) to show how well the topological information is preserved after graph coarsening.

This figure demonstrates the effect of graph reduction rate on the performance of a GCN model for node classification. It shows that the model performs relatively stably even with significant reduction on two datasets while the performance is more sensitive to the reduction rate for another dataset. The t-SNE visualization of node embeddings shows similar patterns of node embeddings between original and coarsened graphs with low reduction rates, while more significant changes are observed with higher reduction rates.

This figure shows a comparison of memory usage across different continual graph learning methods (joint_train, ER_reservior, SSM, SSRM, TACO) over multiple tasks for three different datasets (Kindle, DBLP, ACM). The y-axis represents memory usage in MB, and the x-axis represents the task number. The figure demonstrates that TACO maintains relatively stable memory usage regardless of the number of tasks, while other methods show a more significant increase in memory usage as the number of tasks grows.
More on tables
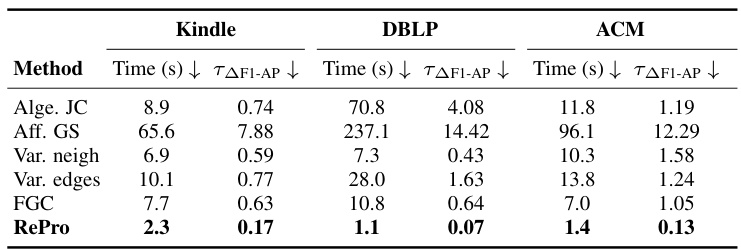
This table presents a comparison of different graph coarsening methods’ performance in terms of computation time and their effect on model performance. The trade-off is calculated as the time required to improve or reduce specific metrics (F1-AP, F1-AF, BACC-AP, BACC-AF) by 1%, compared to a fine-tuning baseline. The results are obtained using the GCN model and averaged over 10 trials on three datasets (Kindle, DBLP, ACM).

This table compares several experience replay-based continual graph learning methods, highlighting their differences in terms of replay buffer contents, graph topology preservation, handling of inter-task edges, and consideration of the dynamic receptive field. A checkmark indicates that the method includes the feature; an ‘X’ indicates it does not. The table helps illustrate the unique aspects of TACO compared to existing methods.
This table presents the results of node classification experiments using a Graph Convolutional Network (GCN) as the backbone model on three different datasets. The table compares the performance of the proposed TACO method against several state-of-the-art continual learning methods. The metrics used for evaluation are Average Performance (AP) and Average Forgetting (AF), calculated using macro F1 scores and balanced accuracy scores (BACC). The results are averaged over 10 independent trials, with standard deviations reported.

This table presents the statistics of three datasets used in the paper: Kindle, DBLP, and ACM. For each dataset, it shows the time period covered, the length of the time interval used to define each task, the total number of tasks, the number of classes, and the total number of items (e-books for Kindle, papers for DBLP and ACM).
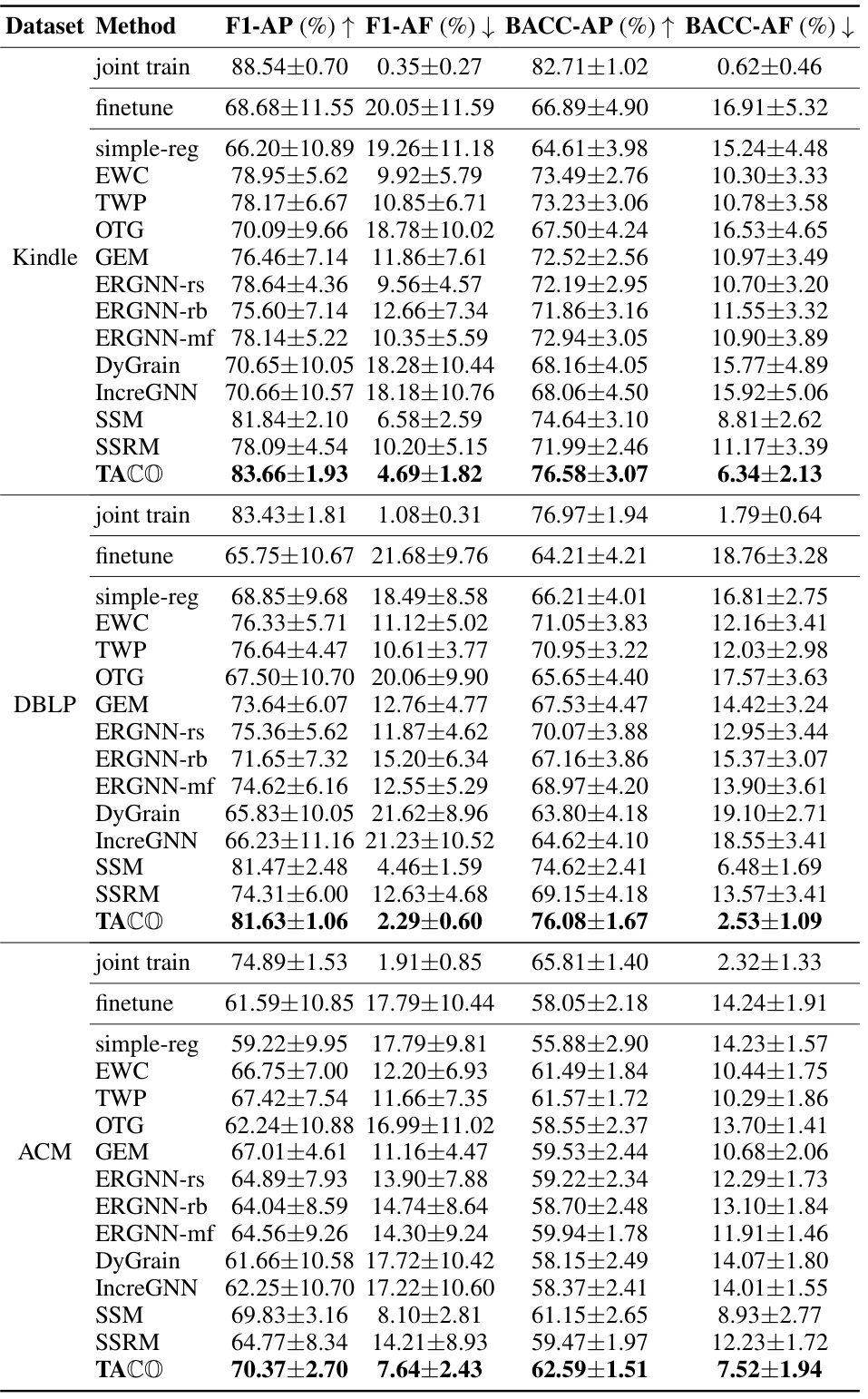
This table presents the results of node classification experiments using the Graph Convolutional Network (GCN) as the backbone model across three datasets: Kindle, DBLP, and ACM. The table compares the performance of TACO (the proposed method) with several state-of-the-art continual learning methods. For each method, the average F1-score and average forgetting (AF) are reported, along with standard deviations across ten trials. The results demonstrate the effectiveness of TACO in reducing catastrophic forgetting in graph neural networks.

This table presents the results of node classification experiments using the Graph Convolutional Network (GCN) model as the backbone. The experiments were conducted on three different datasets (Kindle, DBLP, ACM), and the performance of various continual learning methods (including the proposed TACO method) is evaluated in terms of Average Performance (AP) and Average Forgetting (AF) using macro F1 and Balanced Accuracy scores. Each result represents the average over 10 trials, and the standard deviations are included.
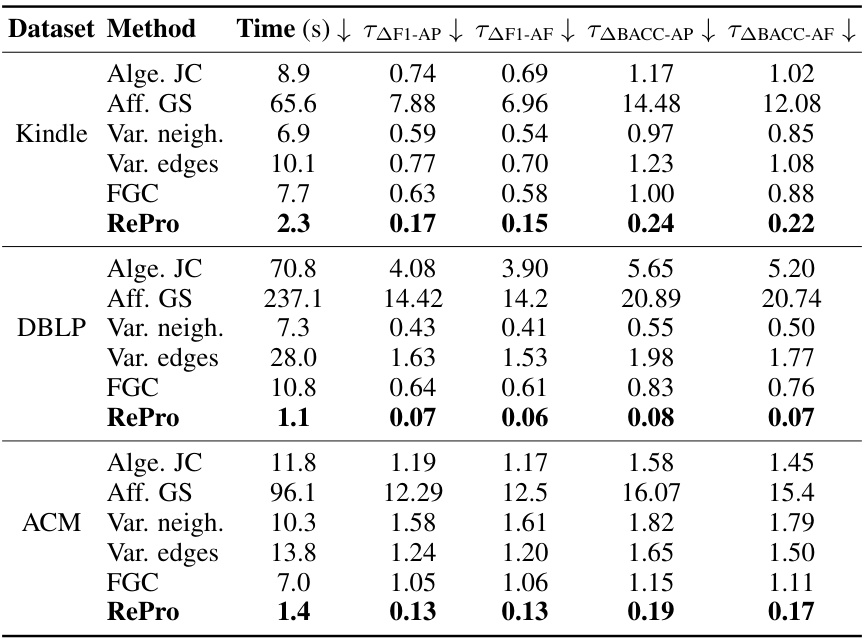
This table presents the computation time and trade-off analysis for various graph coarsening methods used in the TACO framework. The methods are compared across three datasets using the GCN model and the results are averaged over ten trials. The trade-off values represent the coarsening time needed to increase or decrease the performance metrics (F1-AP, F1-AF, BACC-AP, BACC-AF) by 1% compared with the fine-tuning baseline. The best-performing methods for each metric are highlighted in bold.

This table presents the results of short-term forgetting (AF-st) experiment. AF-st measures the decline in model performance on the most recent task when a new task is learned. The table shows the AF-st values (in percentage) for different continual graph learning (CGL) methods on three datasets: Kindle, DBLP, and ACM. The values represent the average F1 score drop on the test set of the most recent task after training on all previous and current tasks. A lower value indicates better performance in retaining knowledge of recent tasks.
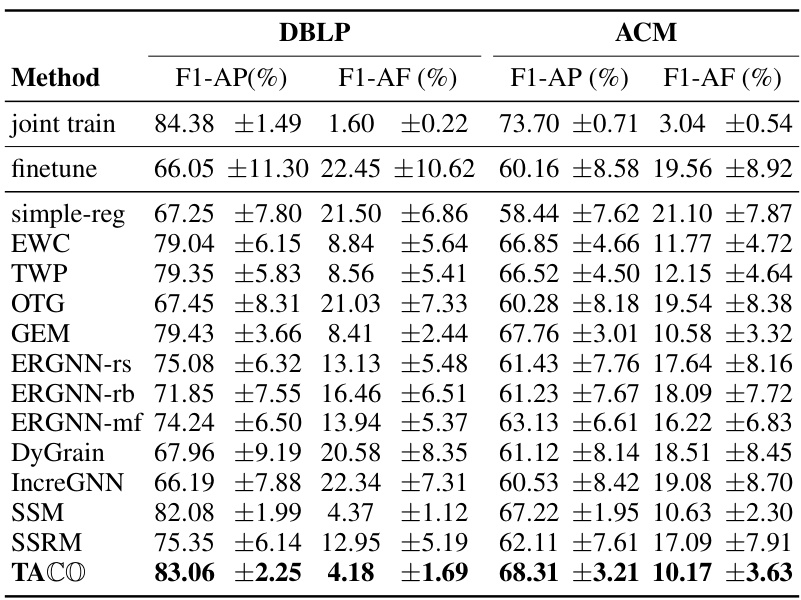
This table presents the results of node classification experiments using a Graph Convolutional Network (GCN) as the backbone model on three different datasets. The performance is measured by Average Performance (AP) and Average Forgetting (AF) using macro F1 and Balanced Accuracy (BACC) as metrics. The table compares the performance of TACO against several state-of-the-art continual learning methods, demonstrating TACO’s superiority. Each method’s performance (AP and AF) is shown for both macro F1 and BACC scores, along with standard deviations across ten trials.

This table presents the average memory usage in MB for each task across different experience-replay based continual graph learning methods. It shows how much memory each method requires to store information about past tasks (replay buffer) during the continual learning process. The methods compared include ERGNN (with different memory update strategies), DyGrain, IncreGNN, SSM, SSRM, and TACO. The table allows a comparison of memory efficiency across various approaches.

This table presents the results of node classification experiments using the Graph Convolutional Network (GCN) model as the backbone on three different datasets: Kindle, DBLP, and ACM. The table compares the performance of various continual learning methods (including the proposed TACO method and several state-of-the-art baselines) in terms of average performance (AP) and average forgetting (AF), using macro F1 and balanced accuracy (BACC) as evaluation metrics. The results are averaged over 10 trials, with standard deviations reported.
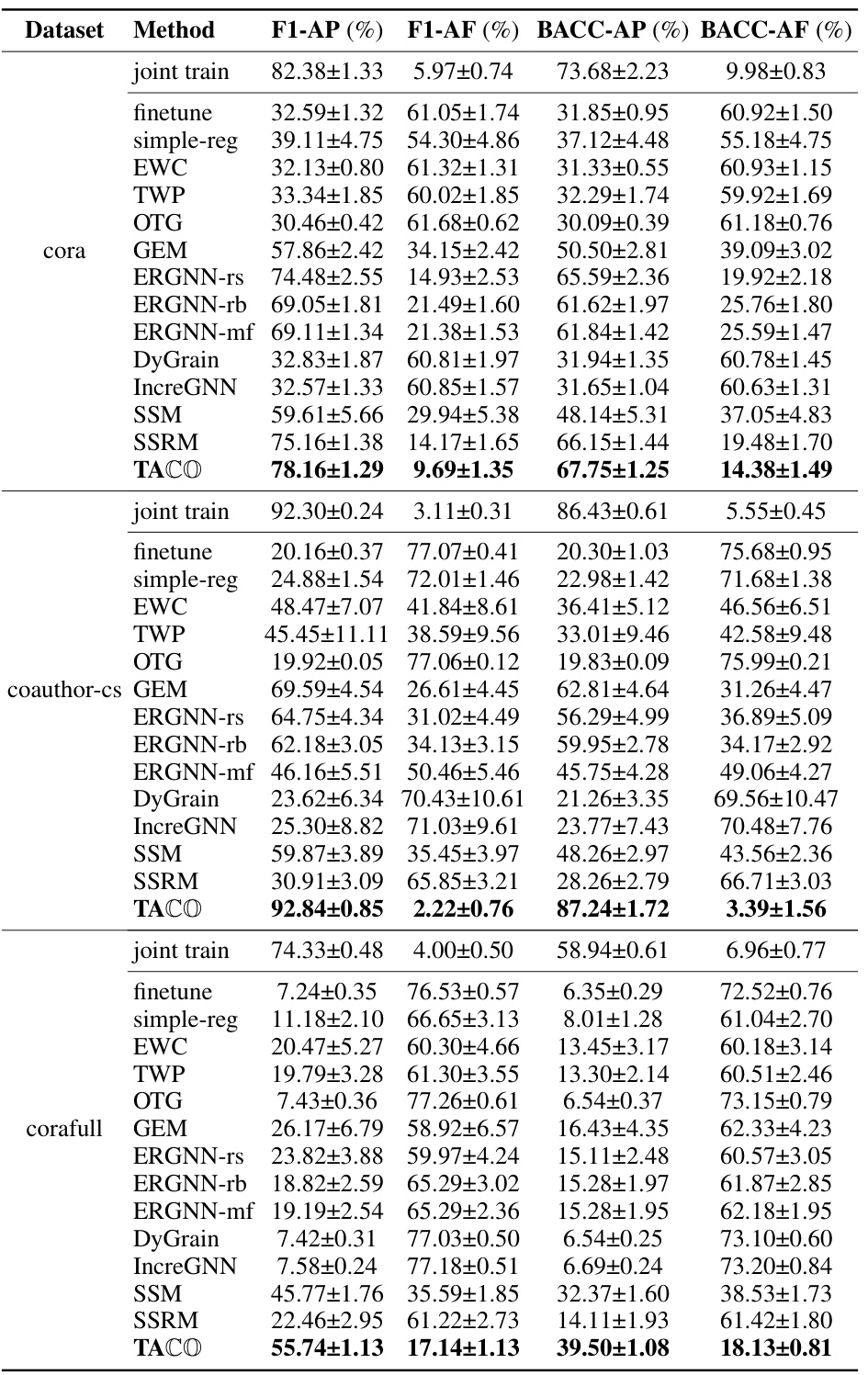
This table presents the results of node classification experiments using Graph Convolutional Networks (GCNs) as the backbone model on three different datasets. The table compares the performance of various continual learning methods, including the proposed TACO method, against several state-of-the-art baselines. Metrics reported include average performance (AP) and average forgetting (AF) using macro F1 and balanced accuracy scores. The results are averaged over ten trials, with standard deviations included.
Full paper#