↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Private deep learning inference, while protecting data and model privacy, suffers from high computational costs. Homomorphic encryption (HE), a promising technique, faces significant latency issues due to the complex operations involved in processing encrypted data. Existing HE-based frameworks struggle with substantial latency overheads, especially for linear layers in deep neural networks (DNNs). Many attempts were made to resolve this issue, but they suffer from limited improvements.
PrivCirNet addresses this problem by introducing a novel co-optimization framework. It leverages block circulant transformation to convert computationally expensive matrix operations into more efficient 1D convolutions optimized for HE. This is coupled with a customized HE encoding algorithm, CirEncode, to enhance compatibility and reduce latency. Furthermore, PrivCirNet uses a latency-aware approach to determine layer-wise block sizes and incorporates layer fusion to further boost efficiency. Experimental results show significant latency reductions and accuracy improvements compared to existing methods on various DNNs and datasets.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in homomorphic encryption and private AI, offering a novel approach to significantly reduce the computational overhead of private deep learning inference. Its co-optimization framework and novel encoding algorithm open new avenues for improving the efficiency and practicality of privacy-preserving machine learning, impacting various sensitive applications. The latency-aware optimization strategy and the demonstration of substantial performance gains over state-of-the-art methods make this research highly relevant to current trends in secure AI.
Visual Insights#

This figure illustrates the hybrid HE/MPC framework for private inference, comparing the latency breakdown of linear and non-linear layers in different models (Bolt, SpENCNN), and showcasing the GEMV operation with a circulant weight matrix. The hybrid approach involves both homomorphic encryption (HE) and multi-party computation (MPC) to protect data privacy during inference. The latency breakdown highlights the significant computational cost of linear layers, which motivates the use of circulant matrices for optimization. The circulant matrix conversion of GEMV enables more efficient computation with HE.
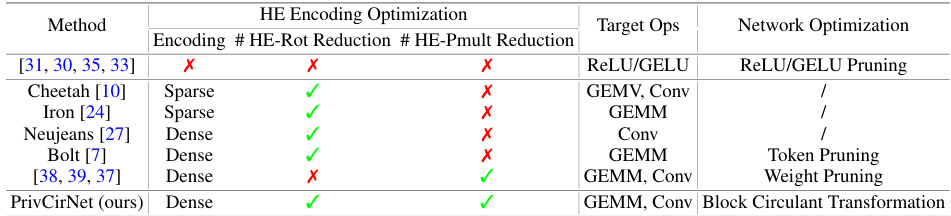
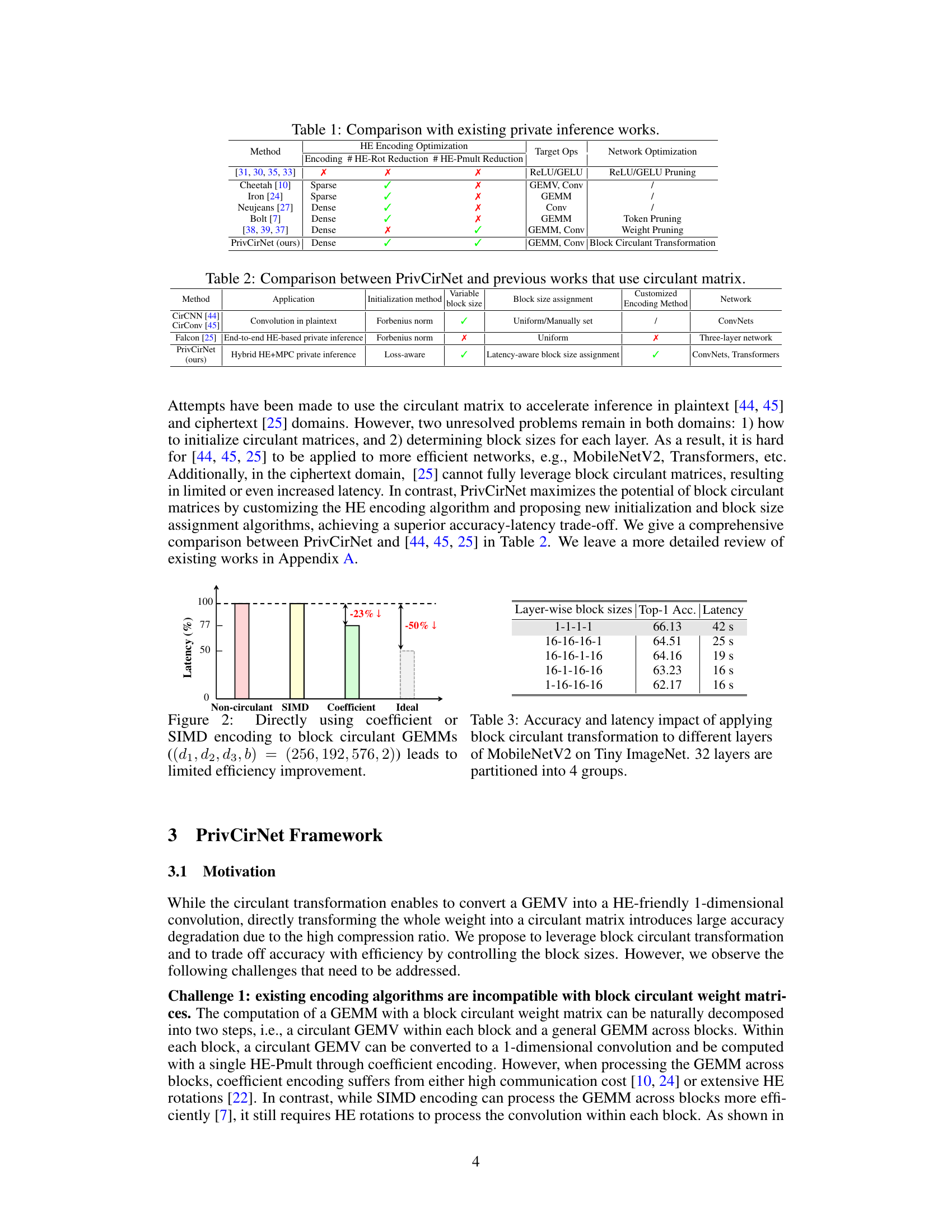
This table compares PrivCirNet with other state-of-the-art private inference methods. It highlights whether each method uses HE encoding optimization, network optimization, and what types of operations are targeted (GEMM, Convolution, etc.). It also indicates which methods reduce the number of HE rotations and/or HE multiplications, and what specific network optimization techniques are employed.
In-depth insights#
Block Circulant GEMM#
The concept of “Block Circulant GEMM” introduces an efficient approach to speed up computation in deep neural networks. It leverages the structure of circulant matrices, which are highly structured and allow for faster computation, particularly within the framework of homomorphic encryption (HE). The “block” aspect suggests a strategy of partitioning larger matrices into smaller circulant blocks, potentially improving performance by enabling parallel processing. This approach aims to offset accuracy losses associated with direct circulant transformations while achieving the speed gains offered by circulant matrix-vector multiplication. A key challenge would be determining the optimal block size, balancing speed improvements with accuracy. Careful consideration of HE-compatible encoding algorithms is also crucial, as it directly influences the overall efficiency of the system. Finally, the approach is promising, particularly in the context of privacy-preserving deep learning where HE is often used, but its feasibility needs to be evaluated on a larger scale to assess the trade-offs between efficiency and model accuracy.
Latency-Aware Design#
A latency-aware design approach for deep learning models prioritizes minimizing the time taken for inference. This is crucial for real-time applications and resource-constrained environments. Key considerations include efficient network architectures (e.g., reducing model size or depth), optimized algorithms (e.g., faster matrix multiplication), and hardware acceleration (e.g., using specialized processors). The design process often involves a trade-off between latency and accuracy, with model compression techniques or quantization being used to reduce computational cost at the expense of some accuracy. Profiling and benchmarking are essential to identify latency bottlenecks and evaluate the impact of design choices. The ultimate goal is to create a model that delivers satisfactory accuracy within the desired latency constraints.
CirEncode Algorithm#
The core idea behind the hypothetical ‘CirEncode Algorithm’ centers on optimizing homomorphic encryption (HE) computations for deep neural networks (DNNs) by leveraging the properties of circulant matrices. The algorithm likely aims to efficiently convert general matrix-vector multiplications (GEMVs) into computationally cheaper 1-dimensional convolutions within a block circulant framework. This is achieved through a co-design of HE encoding and DNN architecture, likely focusing on efficient encoding methods (e.g., coefficient or SIMD) tailored to block circulant matrices. This dual approach seeks to minimize the number of computationally expensive HE rotations and multiplications, leading to a significant speedup. A crucial aspect is the development of a customized HE encoding scheme that leverages the block circulant structure, possibly integrating techniques like DFT for efficient conversion between domains. The ‘CirEncode Algorithm’ might also involve a layer-wise assignment strategy for block sizes, potentially guided by second-order information, to achieve a favorable balance between accuracy and latency.
Network-Protocol Fusion#
Network-protocol fusion, as a concept, aims to tightly integrate the network architecture and the underlying cryptographic protocols used for private inference. This integration seeks to optimize the overall system performance by exploiting synergies between the two. By considering both the network structure and the protocol’s specific requirements simultaneously during the design phase, it’s possible to achieve efficiencies that would be impossible with separate optimization. Careful consideration of the interplay between the choice of network layers, their structure, and the operations performed by the cryptographic protocol is essential. This approach aims to reduce latency and computational overhead, and may involve custom HE encoding algorithms tailored to specific network operations, potentially resulting in a more efficient and privacy-preserving deep learning inference system. A key challenge is designing the encoding algorithms and network layer structures in a manner that works seamlessly together, as this requires careful consideration of the compatibility between them. Another challenge would involve ensuring the fusion doesn’t introduce vulnerabilities while maintaining the original security guarantees.
Future Work Directions#
Future research could explore improving the efficiency of the block circulant transformation by investigating alternative methods for weight matrix conversion or optimizing existing methods for specific network architectures. Addressing the incompatibility between block circulant transformations and existing HE encoding algorithms remains crucial, and developing novel encoding schemes that fully leverage the advantages of this approach could significantly improve performance. Additionally, research into co-designing the encoding algorithm and DNN architectures for improved overall efficiency is warranted. The exploration of layer fusion techniques to further reduce latency and developing methods for adapting PrivCirNet to different DNN architectures and datasets beyond those tested could broaden the framework’s applicability. Finally, rigorous theoretical analysis to assess the trade-offs between accuracy and computational overhead is vital for optimizing PrivCirNet’s performance.
More visual insights#
More on figures
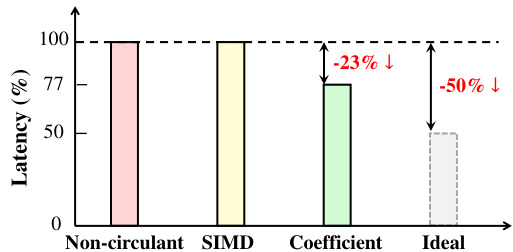
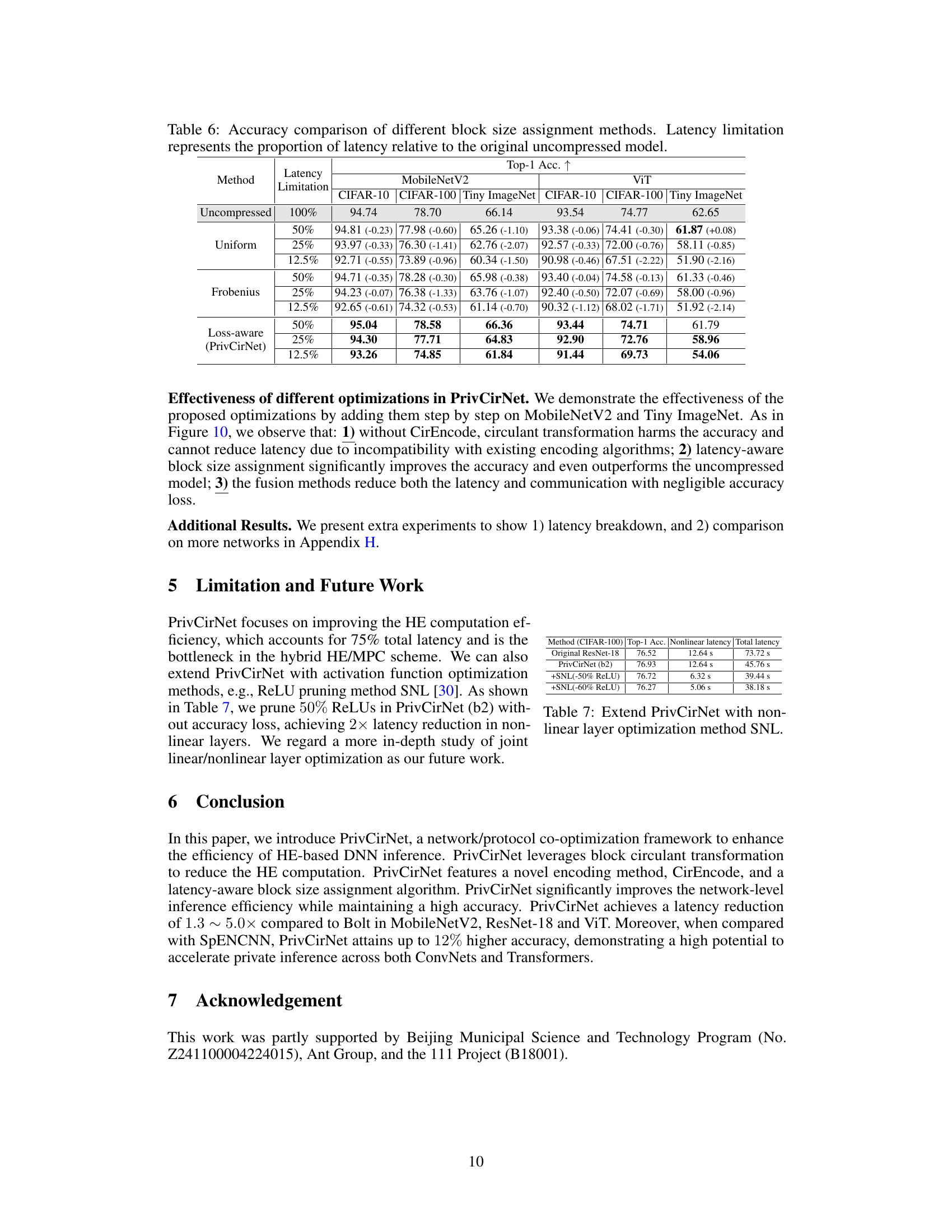
This figure shows the latency comparison of different encoding methods for block circulant GEMMs. The non-circulant method has the highest latency, while the SIMD encoding method has a slightly lower latency than the coefficient encoding method. The ideal latency is 50% lower than the coefficient encoding method. This indicates that using coefficient encoding can significantly improve the efficiency of block circulant GEMMs compared to SIMD encoding.
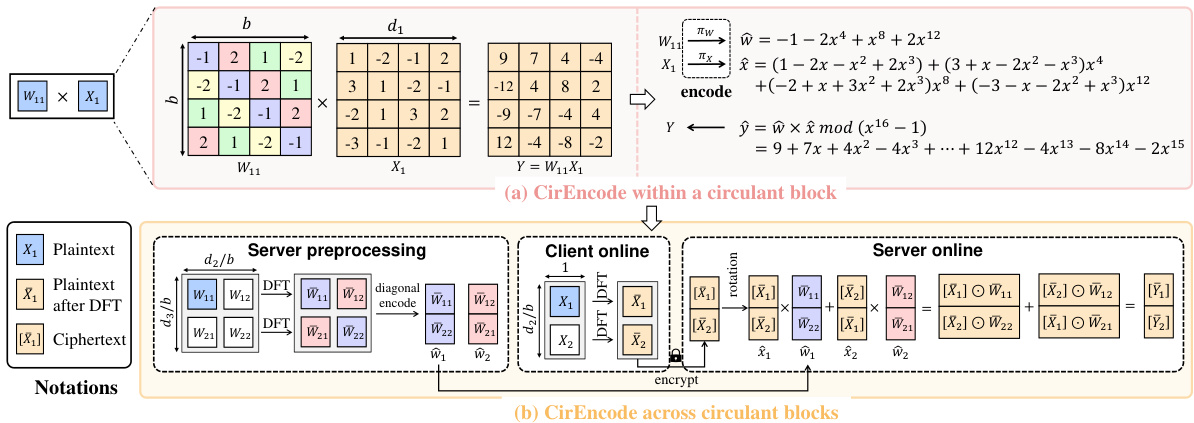
This figure illustrates the CirEncode process for a block circulant GEMM with dimensions (d1, d2, d3, b) = (4, 8, 8, 4). It shows how CirEncode handles both encoding within a circulant block (a) and across circulant blocks (b). Panel (a) details how individual circulant blocks are encoded using a coefficient encoding scheme that avoids HE rotations, converting the GEMV into a HE-friendly 1D convolution. Panel (b) shows how the across-block GEMM is handled using SIMD encoding. This combined approach aims to reduce HE rotations and multiplications.

This figure shows the overall framework of PrivCirNet. It is divided into two main parts: Protocol Optimization and Network Optimization. Protocol Optimization focuses on the CirEncode algorithm (Section 3.2) which provides support for a latency-aware block size assignment. Network Optimization (Section 3.3) handles the layer-wise block size assignments and network-protocol co-fusion (Section 3.4).

This figure visualizes the sensitivity of different block sizes on the loss function for each layer in a Vision Transformer (ViT) model trained on CIFAR-100. It compares two initialization methods: one using the Frobenius norm and the other using the proposed loss-aware initialization (Ω₁). The top panels show the sensitivity of each linear layer to different block sizes (b=1, 2, 4, 8, 16), while the bottom panels show the selected block sizes for each layer. The loss-aware method shows more variability across layers and better captures the effects of varying block sizes on task loss.
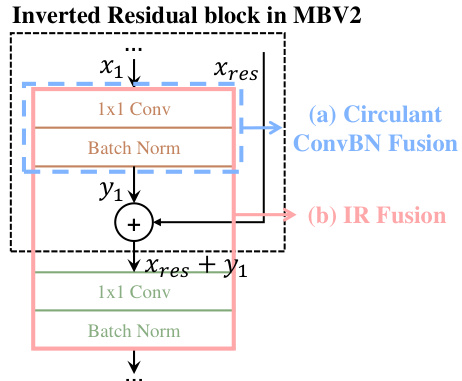
This figure illustrates two optimization strategies employed in PrivCirNet for improving efficiency. (a) shows Circulant ConvBN Fusion, where convolution and batch normalization layers are fused to maintain the block circulant structure and reduce latency. (b) presents IR (Inverted Residual) Fusion Protocol, which fuses consecutive linear layers in the network to reduce communication overhead.

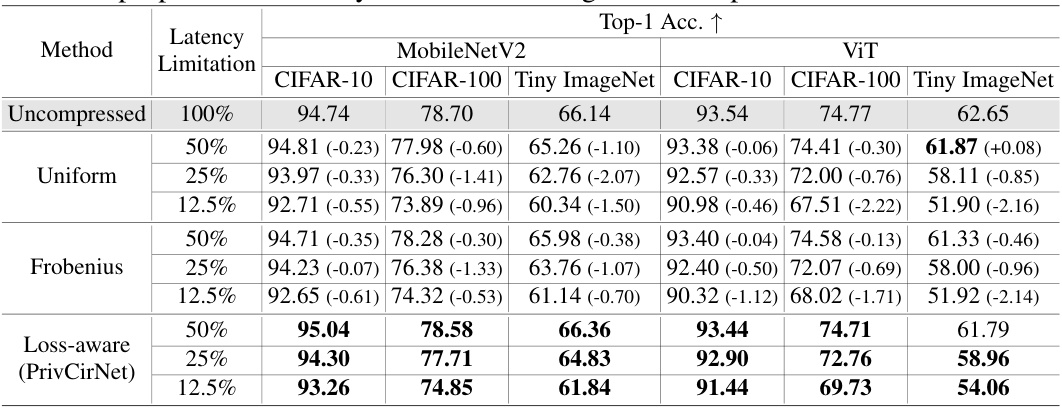
This figure compares the latency of different homomorphic encryption (HE) protocols for performing general matrix multiplications (GEMMs) and convolutions. The protocols compared include CrypTFlow2, Cheetah, Neujeans, Bolt, and PrivCirNet. PrivCirNet is shown with two different block sizes (b=2 and b=8), demonstrating the effect of block size on latency. The results show that PrivCirNet significantly outperforms the other methods in terms of latency, especially with the larger block size (b=8). The x-axis shows different GEMM and convolution dimensions, representing various layer configurations in typical neural network architectures. The y-axis represents the latency in seconds.
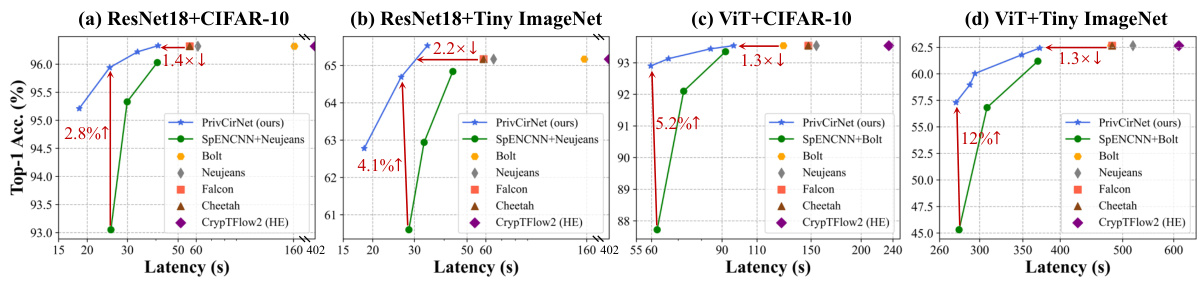
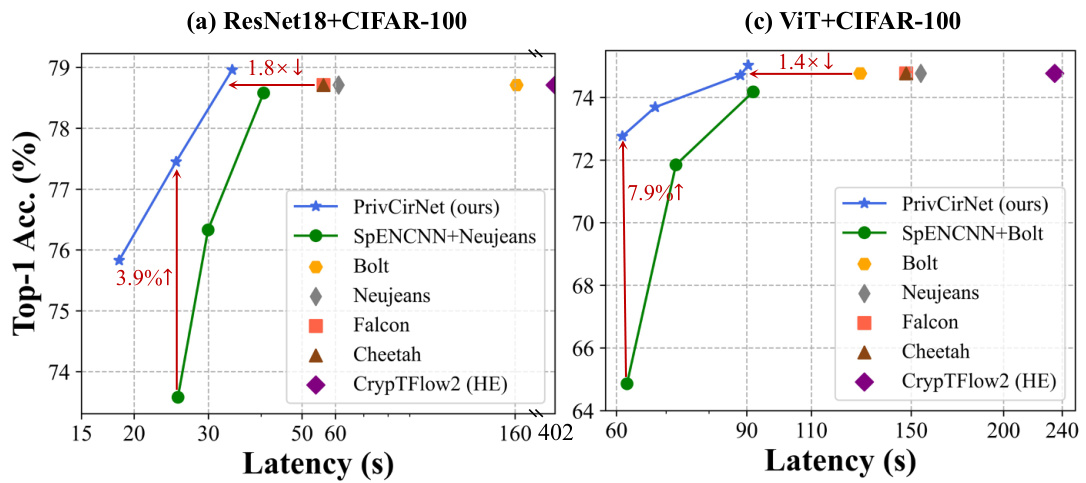
This figure compares the performance of PrivCirNet with SpENCNN and other state-of-the-art private inference protocols (Bolt, Neujeans, Falcon, Cheetah, CrypTFlow2) on MobileNetV2 across four datasets (CIFAR-10, CIFAR-100, Tiny ImageNet, and ImageNet). The Pareto front is shown, illustrating the trade-off between latency and accuracy. PrivCirNet demonstrates significant latency reductions and accuracy improvements compared to the baselines, especially on larger datasets like ImageNet.

This ablation study shows the impact of each component of PrivCirNet on MobileNetV2, using Tiny ImageNet as the dataset. It demonstrates that the combination of all optimizations leads to the best performance. The individual components are: 1. Baseline MobileNetV2: The original model without any PrivCirNet optimizations. 2. + Cir. Transformation (b=2): The model with only block circulant transformation applied (with block size b=2). 3. + CirEncode (Sec. 3.2): Adds the CirEncode encoding method to the model. 4. + Latency-aware block size assignment (Sec. 3.3): The layer-wise block sizes are optimized for latency. 5. + ConvBN Fusion (Sec. 3.4): Convolution and batch normalization layers are fused. 6. + IR Fusion (Sec. 3.4): Inverted residual blocks are fused. The figure shows the latency (in seconds), communication (in MB), and top-1 accuracy (%) for each stage.
This figure is composed of four subfigures. Subfigure (a) illustrates a hybrid HE/MPC framework for private inference, where linear layers are processed using HE, and non-linear layers are processed using MPC. Subfigure (b) shows the breakdown of latency for linear and non-linear layers in Bolt’s protocol. Subfigure (c) compares the latency breakdown of linear layers in a standard model and a SpENCNN model with 50% sparsity. Finally, subfigure (d) illustrates the GEMV (general matrix-vector multiplication) operation using a circulant weight matrix, which is a key concept in the proposed method.

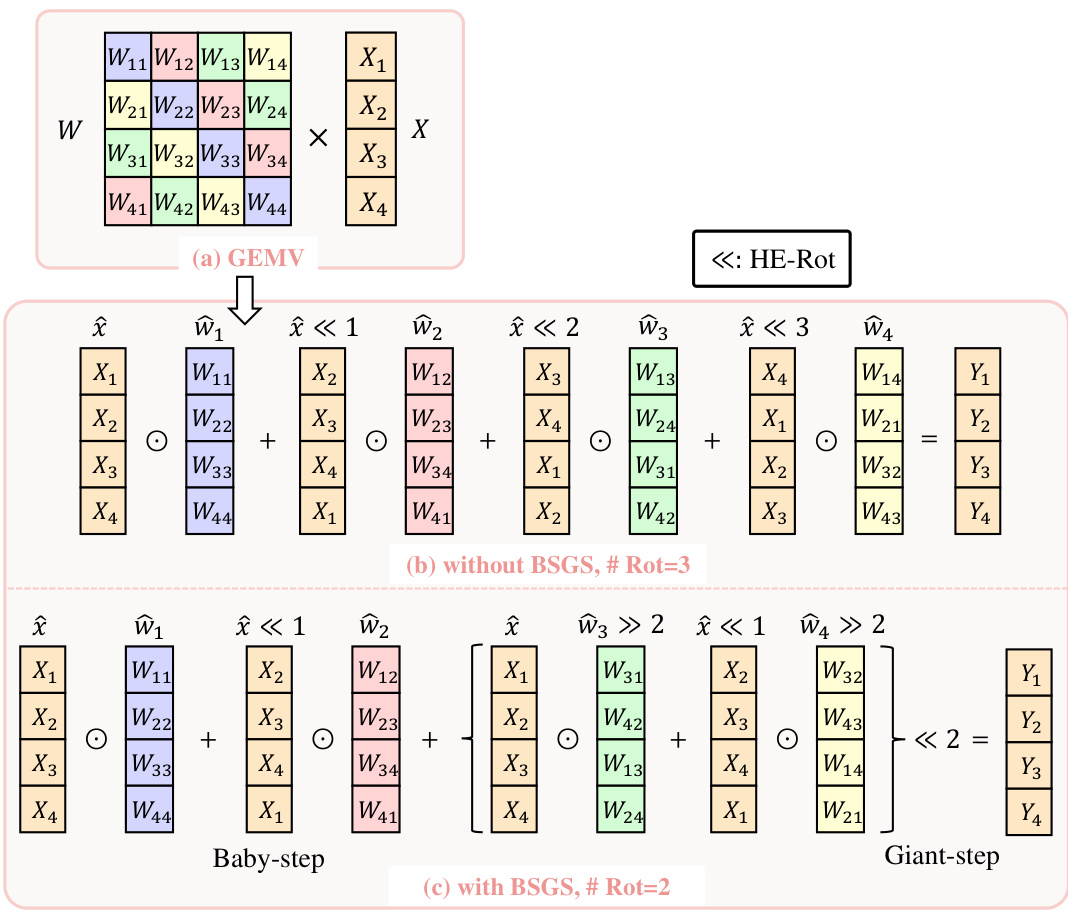
This figure illustrates the authors’ adaptation of the Baby-step Giant-step (BSGS) algorithm for block circulant General Matrix-Vector Multiplication (GEMM). The BSGS algorithm reduces the number of costly homomorphic rotations. The figure shows how tiling is used to split matrices into smaller blocks whose maximum size is limited by the HE polynomial degree, and how the BSGS parameters B (number of baby steps) and G (number of giant steps) are determined to minimize the number of rotations while adhering to the constraints of the tiling and polynomial degree.

This figure illustrates the CirEncode process for a block circulant GEMM. Panel (a) shows CirEncode within a circulant block, detailing how a block circulant GEMV is converted into a HE-friendly 1D convolution using coefficient encoding. Panel (b) illustrates CirEncode across circulant blocks, explaining how SIMD encoding handles GEMMs across blocks, combining the advantages of both encoding methods for enhanced efficiency. The notations used in this figure are defined within the paper.
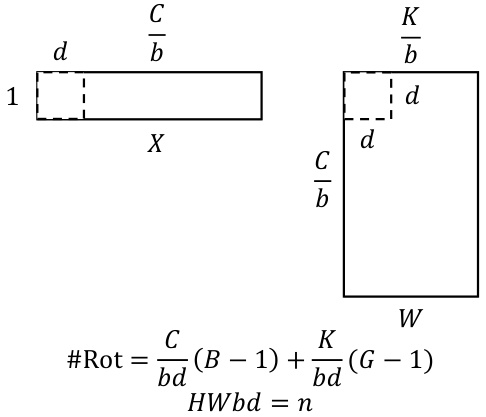
This figure illustrates the authors’ enhanced Baby-step Giant-step (BSGS) algorithm for block circulant General Matrix-Vector Multiplication (GEMM). It shows how tiling is used to divide the GEMM into smaller blocks that are compatible with the limitations of Homomorphic Encryption (HE) polynomial degree. The formula #Rot = (d1d2/n)(B-1) + (d1d3/n)(G-1) shows the number of rotations required, where B and G are the numbers of baby-steps and giant-steps respectively, and n is the polynomial degree. The constraint HWbd = n ensures that the tile size is within HE’s limitation. This optimized approach reduces the number of rotations needed for the GEMM computation compared to the standard BSGS algorithm.

This figure illustrates why structured pruning is not effective with the BSGS algorithm. In BSGS, rotations are split into baby-step and giant-step rotations. To reduce rotations, diagonals across different groups must be pruned, and for tiling, diagonals across all groups for all weight matrices must be pruned. This makes it difficult to reduce the number of rotations using structured pruning.
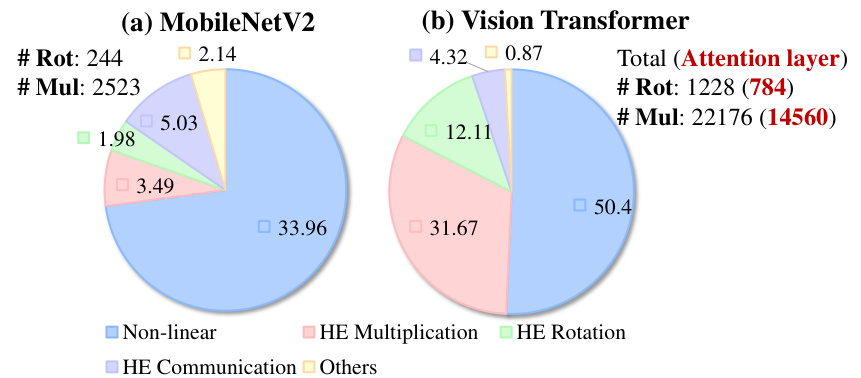
This figure illustrates the Hybrid HE/MPC framework for private inference (a), compares latency breakdowns of linear and non-linear layers in Bolt’s protocol and SpENCNN (b, c), and shows a GEMV operation with a circulant weight matrix (d) which is the core concept of the proposed method.
This figure visualizes the sensitivity of each layer to block size changes (b) during the block circulant transformation of a Vision Transformer (ViT) model trained on the CIFAR-100 dataset. It compares two initialization methods: one using the Frobenius norm and the other using the proposed loss-aware initialization (Ω₁). The x-axis represents the linear layer index, and the y-axis represents the sensitivity (Ω₁) or the Frobenius norm. The plots show how the sensitivity to block size varies across different layers, indicating the importance of a layer-wise block size assignment strategy rather than a uniform block size for all layers.

This figure compares the latency of various protocols (CrypTFlow2, Cheetah, Neujeans, Bolt, and PrivCirNet) for performing GEMMs (general matrix multiplications) and convolutions on different dimensions. PrivCirNet uses circulant weight matrices with varying block sizes (b2 and b8). The results demonstrate that PrivCirNet, particularly with block size 8, significantly reduces the latency compared to other protocols.
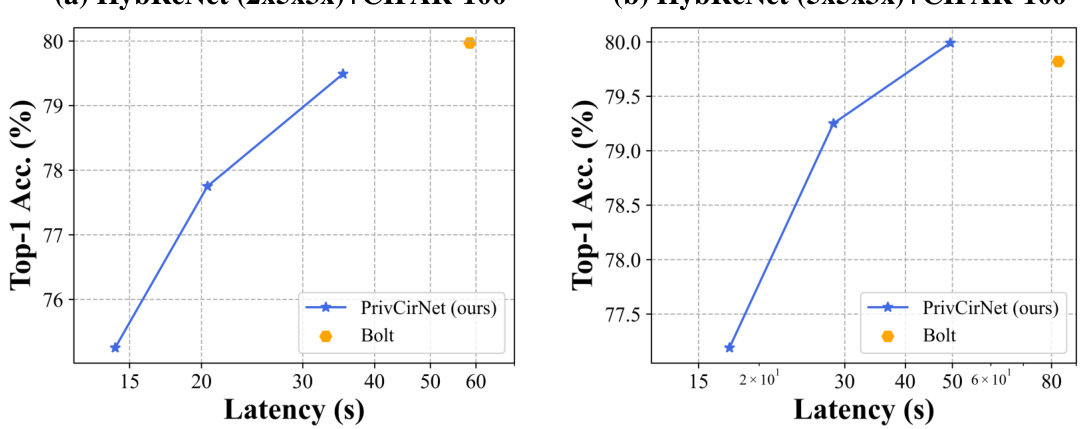
This figure compares the performance of PrivCirNet with SpENCNN and other state-of-the-art protocols (Bolt, Neujeans, Falcon, Cheetah, and CrypTFlow2) on MobileNetV2 for different datasets (CIFAR-10, CIFAR-100, and Tiny ImageNet). It shows accuracy and latency trade-offs. PrivCirNet consistently demonstrates superior performance in terms of both latency and accuracy improvements compared to the baselines.
More on tables

This table compares PrivCirNet with three other methods that utilize circulant matrices for efficient inference. It highlights key differences in their application (plaintext convolution vs. private inference), initialization methods for the circulant matrices, whether they use variable block sizes, their block size assignment strategies, and whether they employ customized encoding methods. The table also notes the types of neural networks each method is designed for.

This table shows the results of applying block circulant transformation with different block sizes to different layers of the MobileNetV2 model on the Tiny ImageNet dataset. The 32 layers of the model are divided into 4 groups. Each row shows a different layer-wise block size assignment, its corresponding Top-1 accuracy, and the resulting inference latency. This demonstrates how the choice of block size affects both accuracy and efficiency.
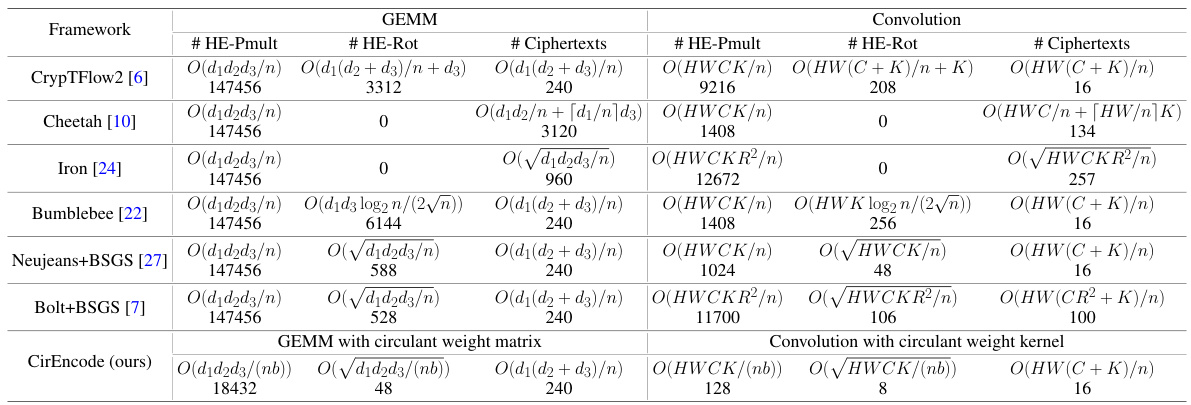
This table provides a comparison of the theoretical computational complexity of the CirEncode algorithm with several existing algorithms for both general matrix multiplication (GEMM) and convolution operations. The comparison is based on the number of homomorphic encryption (HE) multiplications (# HE-Pmult), HE rotations (# HE-Rot), and ciphertexts used. The table shows that CirEncode significantly reduces the number of HE-Rot and HE-Pmult compared to state-of-the-art methods, particularly when using block circulant matrices, demonstrating the efficiency gains achieved through its novel encoding algorithm.

This table compares the number of homomorphic encryption (HE) rotations (HE-Rot) and HE multiplications (HE-Pmult) required by different protocols (Neujeans+BSGS, Bolt+BSGS, PrivCirNet (b2), and PrivCirNet (b8)) for general matrix multiplications (GEMMs) and convolutions. Different dimensions of GEMMs and convolutions are considered, reflecting those found in MobileNetV2, ViT, and ResNet-18 architectures. The results demonstrate PrivCirNet’s efficiency in reducing both HE-Rot and HE-Pmult operations, especially with larger block sizes (b8).
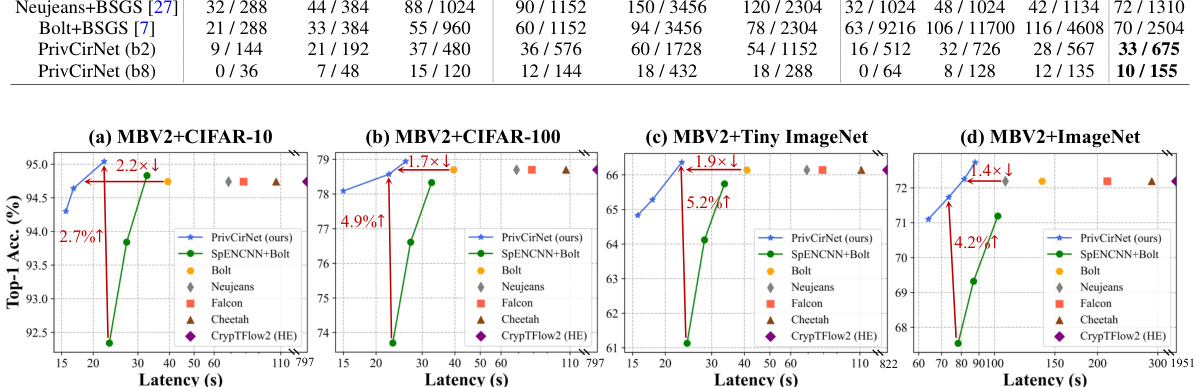
This table compares the number of homomorphic encryption rotations (HE-Rot) and multiplications (HE-Pmult) required by different protocols (Neujeans+BSGS, Bolt+BSGS, PrivCirNet (b2), PrivCirNet (b8)) for both general matrix multiplications (GEMMs) and convolutions. The comparison is done for various dimensions of GEMMs and convolutions, representing different layers and operations in deep neural networks, such as MobileNetV2, ViT, and ResNet-18. The numbers illustrate the computational efficiency gains achieved by PrivCirNet, especially with larger block sizes (b8), significantly reducing the number of HE operations compared to the state-of-the-art methods, Bolt and Neujeans.
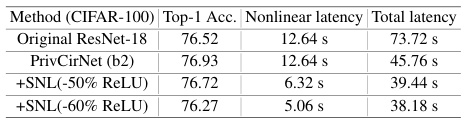
This table compares the Top-1 accuracy results of different block size assignment methods (Uniform, Frobenius, and Loss-aware) for MobileNetV2 and ViT models on CIFAR-10, CIFAR-100, and Tiny ImageNet datasets. The comparison is performed at various latency limitations (50%, 25%, and 12.5%) relative to the uncompressed model’s latency. The table shows the impact of different block size strategies on model accuracy and reveals how the loss-aware method (PrivCirNet) achieves superior accuracy across various datasets and latency constraints.
This table compares the latency of different homomorphic encryption (HE) protocols for general matrix multiplications (GEMMs) and convolutions. It shows the latency achieved by different protocols such as CrypTFlow2, Cheetah, Neujeans, Bolt, and PrivCirNet with different block sizes (b2 and b8). The GEMM dimensions are chosen from various layers of MobileNetV2 and ViT, while convolution dimensions come from ResNet-18. The comparison highlights the latency reduction achieved by PrivCirNet, especially when using a larger block size.

This table compares the theoretical computational complexity of the proposed CirEncode algorithm with existing state-of-the-art HE encoding methods (CrypTFlow2, Cheetah, Iron, Bumblebee, Neujeans+BSGS, Bolt+BSGS). The comparison is performed for both GEMM (General Matrix Multiplication) and convolution operations, considering the number of homomorphic multiplications (# HE-Pmult), homomorphic rotations (# HE-Rot), and the number of ciphertexts used. The table highlights the significant reduction in computational complexity achieved by CirEncode, especially in terms of HE rotations, due to its utilization of block circulant matrices and the optimized BSGS algorithm.

This table presents the key characteristics of the different deep neural network models (MobileNetV2, ResNet-18, and ViT) used in the PrivCirNet experiments. It shows the number of layers in each model, the number of parameters (in millions), the number of multiply-accumulate operations (in billions), and the datasets used for evaluation. This information is essential for understanding the scope and scale of the experimental results presented in the paper.

This table presents the accuracy and latency results obtained by combining PrivCirNet and DeepReshape, a method for optimizing ReLU layers. Different configurations of DeepReshape are tested, each with a varying percentage of ReLU units removed (-53%, -50%, -72%). The results show the Top-1 accuracy and latency breakdown for linear and non-linear layers for each configuration.
Full paper#