Nonparametric Instrumental Variable Regression through Stochastic Approximate Gradients

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in causal inference and nonparametric statistics because it presents a novel, flexible algorithm (SAGD-IV) for nonparametric instrumental variable regression. It offers superior stability and competitive performance compared to existing methods, and importantly, it readily handles binary outcomes and flexible loss functions—challenges commonly encountered in real-world applications. This opens avenues for more robust causal analysis in diverse settings.

Visual Insights

#

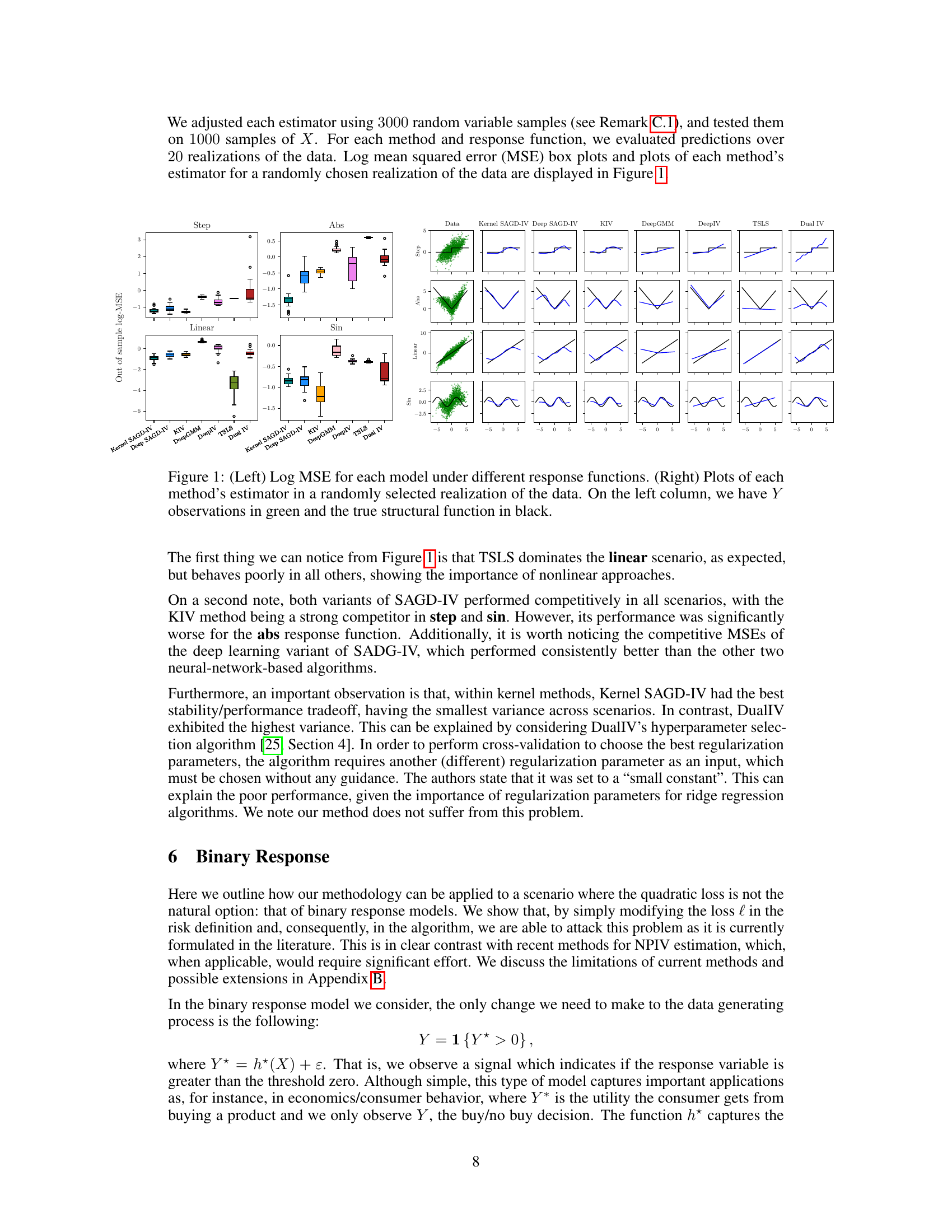
This figure presents the results of applying different methods (Kernel SAGD-IV, Deep SAGD-IV, KIV, DeepGMM, DeepIV, TSLS, Dual IV) to estimate the structural function in a continuous response setting. The left panel shows the log mean squared error (MSE) for each method across different response functions (Step, Abs, Linear, Sin), demonstrating their performance and stability. The right panel shows the estimated structural function for one random realization of the data, where the green dots represent the observations and the black line represents the true structural function. This comparison illustrates the ability of each method to recover the true underlying function.

This figure presents a comparison of different methods for estimating the structural function in a causal inference problem with continuous response variables. The left panel shows box plots of the log mean squared error (MSE) for each method across different response functions (step, abs, linear, and sin), providing a summary of their performance. The right panel shows the estimated functions for one representative run of the experiment for each method, allowing for a visual comparison against the true structural function.

In-depth insights

#

NPIV Risk Minimization

#

Nonparametric Instrumental Variable Regression (NPIV) presents a significant challenge due to its ill-posed inverse problem nature. Risk minimization offers a powerful approach to address this, formulating the problem as the search for a function minimizing the expected loss between the conditional expectation of the outcome given the instrument and a transformation of the causal function. This approach elegantly sidesteps the need for direct estimation of the often-unstable inverse operator, offering enhanced stability. The choice of loss function becomes crucial, with the paper exploring both quadratic and non-quadratic losses (like the binary cross entropy for binary outcomes), highlighting the flexibility of this framework. Stochastic gradient descent in a functional space provides a practical algorithmic solution for minimizing the risk, offering theoretical guarantees in terms of excess risk bounds. The method’s flexibility extends to the choice of function approximators (neural networks, kernel methods), providing a versatile tool for a wider range of applications.

SAGD-IV Algorithm

#

The SAGD-IV algorithm, a novel approach to nonparametric instrumental variable regression, is presented. SAGD-IV directly minimizes the population risk, deviating from existing methods which focus on empirical risk minimization or moment conditions. This is achieved through a functional stochastic gradient descent method, where the gradient is analytically computed and estimated stochastically, allowing flexible estimator choices (neural networks or kernel methods). The theoretical guarantees provided include bounds on excess risk, demonstrating the method’s stability and competitive performance. A key advantage is its natural extension to binary outcomes, addressing a limitation of many current NPIV methods.

Binary Outcome NPIV

#

In the context of Nonparametric Instrumental Variable regression (NPIV), handling binary outcomes presents unique challenges. Traditional NPIV methods often rely on assumptions like additive noise and quadratic loss functions, which are violated when dealing with binary data. A key difficulty is that the standard additive noise model does not directly apply; the relationship between the dependent variable and predictors is more complex, often involving a latent continuous variable linked to the observed binary outcome through a threshold. This necessitates modifications to the loss function, for instance, employing a binary cross-entropy loss, to better capture the probability of the binary outcome. Existing NPIV algorithms often struggle to adapt to these changes. This is due to the underlying theoretical assumptions used in their design. Therefore, a novel approach is required that directly addresses these issues such as modifying the loss function or adopting a different approach to estimation altogether. The development of new algorithms specifically tailored for binary outcome NPIV is a significant area of research that can provide critical advancements for causal inference in a broader range of applications where binary outcomes are prevalent.

Estimator Comparisons

#

A robust comparative analysis of estimators is crucial for evaluating the effectiveness of a new method. This would involve benchmarking against state-of-the-art methods across multiple datasets, varying in size and characteristics. Key metrics such as MSE, runtime, and stability (resistance to noise or hyperparameter sensitivity) should be carefully examined. The analysis should explore the performance across different settings and identify specific scenarios where one estimator significantly outperforms others, highlighting the strengths and weaknesses of each approach. Theoretical comparisons, based on convergence rates or error bounds, would add another layer of rigor, offering insights into the estimators’ inherent properties and expected behavior. Finally, discussing the computational cost of each estimator is important for practical implementation, particularly when dealing with large datasets.

Future Work & Limits

#

Future work could explore extending the nonparametric instrumental variable regression (NPIV) method to handle more complex data structures, such as those with high dimensionality or non-additive noise. Addressing the computational cost associated with NPIV, particularly for large datasets, is crucial. Further theoretical analysis could focus on refining the risk bounds and investigating the algorithm’s asymptotic properties under weaker assumptions. The current limitations stem from reliance on the additive noise assumption, which may not always hold in practice. Future research should explore robust approaches that relax this assumption and accommodate different noise distributions or structural models. Another significant limitation is the need for consistent estimators of the conditional expectation operator and density ratio, warranting further exploration of improved estimation techniques, including those leveraging recent advancements in machine learning. Finally, assessing the sensitivity of the method to the choice of hyperparameters and providing guidance for optimal selection are key considerations for practical applications. Investigating the applicability of the proposed methodology to various causal inference tasks, beyond continuous and binary outcomes, is a promising area for future exploration.

More visual insights

#

More on figures

This figure presents a comparison of different methods for nonparametric instrumental variable regression in terms of their log mean squared error (MSE) and estimated functions. The left panel shows boxplots of the log MSE for each method across different response functions (step, abs, linear, sin). The right panel shows plots of the estimated functions from each method against the true structural function (in black) and observed data (in green) for a randomly selected data realization. This illustrates the performance of each method in approximating the true causal relationship across various functional forms.

The left side of the figure shows boxplots of the log mean squared error for each of the methods (Kernel SAGD-IV, Deep SAGD-IV, KIV, DeepGMM, DeepIV, TSLS, Dual IV) across different response functions (Step, Abs, Linear, Sin). The right side of the figure shows plots of the estimated structural functions obtained with each method compared to the actual structural function and the observed data points for a randomly chosen realization of the data.

Full paper

#