↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Large language models (LLMs) struggle with complex, multi-step reasoning in advanced mathematical problems. Current methods like Tree of Thought (ToT) and Graph of Thought (GoT) are limited in their effectiveness and generalizability. These approaches often require specific prompts tailored to individual problems, hindering their applicability to diverse scenarios. This necessitates the development of a more robust and versatile solution.
The researchers propose the Multi-Agent System for Condition Mining (MACM) prompting method. MACM addresses the limitations of existing methods by employing a multi-agent interactive system. It extracts the conditions and objectives of a problem, iteratively mining new conditions that aid in achieving the objective. This approach improves accuracy by over 10 percentage points and exhibits strong generalizability across various mathematical contexts. In experiments, MACM increased GPT-4 Turbo’s accuracy in solving challenging mathematical problems by over 20%, significantly outperforming previous state-of-the-art techniques.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel prompting method, MACM, that significantly improves the accuracy of large language models (LLMs) in solving complex mathematical problems. MACM addresses the limitations of existing prompting methods by incorporating a multi-agent system for iterative condition mining, enhancing both accuracy and generalizability. This opens new avenues for leveraging LLMs in fields requiring precise mathematical reasoning, such as scientific research and engineering, and provides valuable insights into prompting engineering techniques.
Visual Insights#
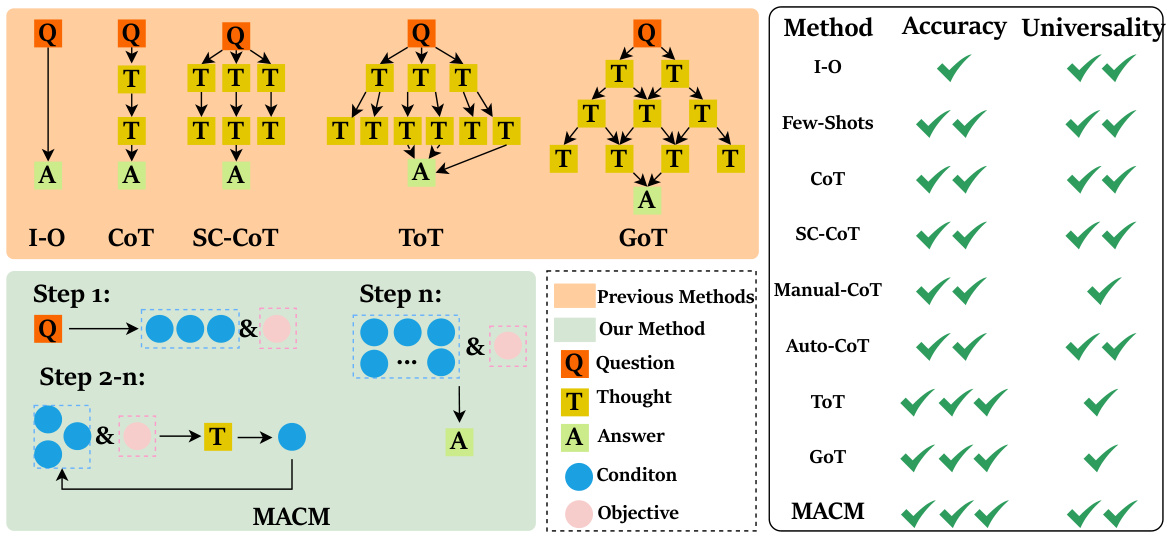
This figure compares various prompting methods, including I-O, CoT, SC-CoT, ToT, and GoT, with the proposed method MACM. It visually represents the structure of each method using a tree-like structure, highlighting the differences in their approach to problem-solving. It also provides a table summarizing the accuracy and universality of each method, showing that MACM excels in both aspects. The figure illustrates how MACM moves beyond the limitations of existing methods by iteratively mining conditions to reach the solution, rather than relying on pre-defined prompts.

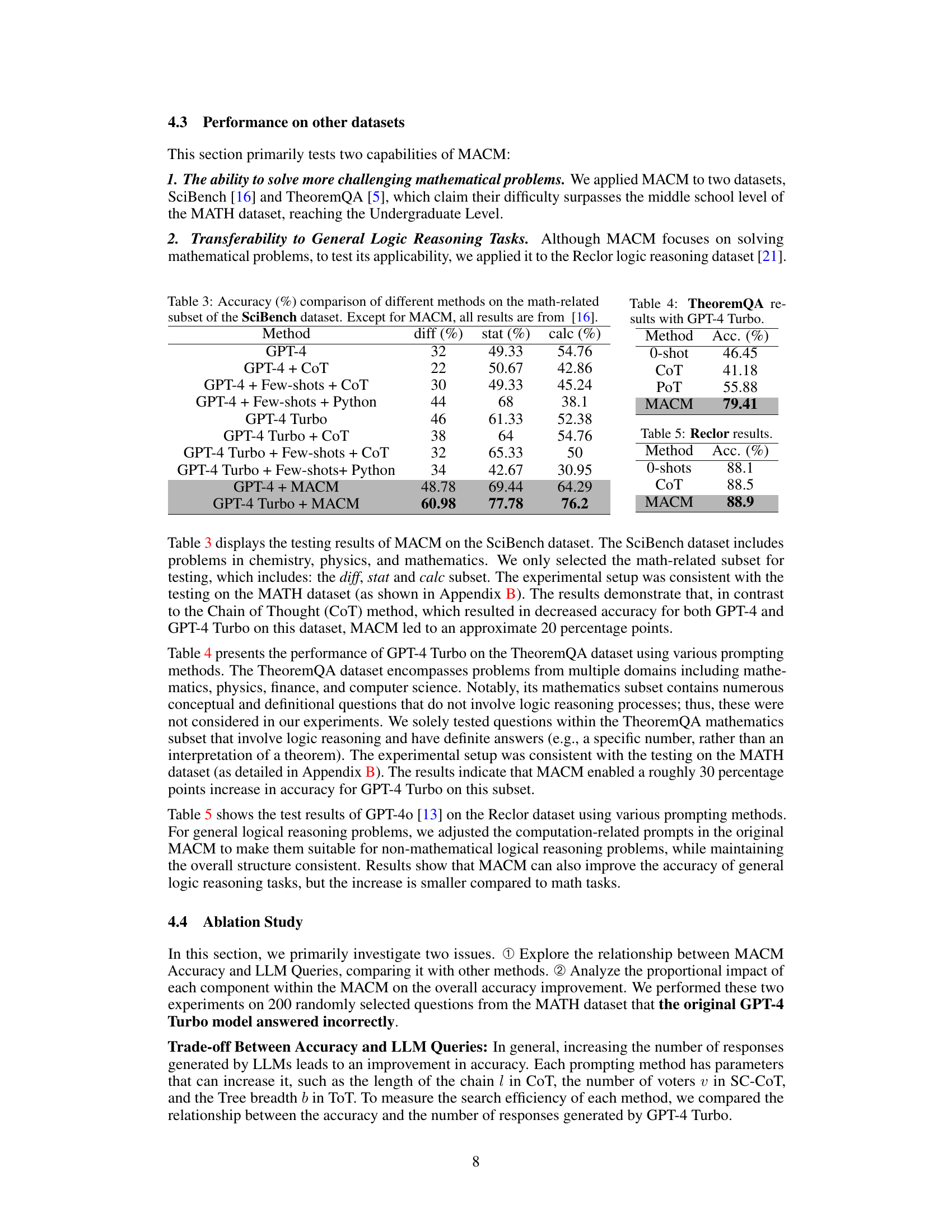
This table compares the accuracy of GPT-4 Turbo on the MATH dataset using various prompting methods, including I-O, CoT, SC-CoT, CSV, CSV+Voting, and MACM. It shows the accuracy percentages achieved by each method across different problem types within the MATH dataset (Algebra, Geometry, Probability, Number Theory, etc.) and an overall accuracy. The results highlight MACM’s significant improvement over other methods.
In-depth insights#
MACM: Multi-Agent Approach#
The proposed MACM (Multi-Agent System for Condition Mining) approach presents a novel framework for enhancing the problem-solving capabilities of large language models (LLMs) in complex mathematical problems. MACM moves beyond the limitations of existing prompting methods like Chain of Thought and Tree of Thought by employing a multi-agent system comprising a Thinker, Judge, and Executor. The Thinker abstracts the problem’s conditions and objective, generating potential solutions and conditions. The Judge evaluates the validity and relevance of these generated conditions, while the Executor executes calculations based on verified conditions. This iterative process of condition mining ensures the LLM progressively gathers sufficient information to achieve the objective, improving accuracy and generalizability across diverse mathematical problems. The key strength of MACM lies in its ability to abstract problem conditions and objectives, reducing reliance on problem-specific prompts and promoting scalability. The experimental results show that MACM significantly enhances the accuracy of LLMs on various mathematical datasets compared to existing methods, especially in complex and challenging problems. This multi-agent interactive approach represents a substantial advancement in LLM prompting techniques. However, the computational cost due to multiple LLM invocations and the performance limitations observed in geometry problems remain as areas for future development.
Prompt Engineering Advance#
Prompt engineering has significantly advanced the capabilities of large language models (LLMs) in complex tasks. Early methods like Chain of Thought (CoT) improved reasoning by prompting the model to generate intermediate steps. However, CoT’s effectiveness was limited, especially in complex mathematical problems. Subsequent techniques such as Tree of Thought (ToT) and Graph of Thought (GoT) addressed this limitation by employing more sophisticated prompting strategies, using tree-like or graph-like structures to guide the reasoning process. Despite these advancements, a critical shortcoming remained: the lack of generalizability. ToT and GoT often required problem-specific prompts, limiting their applicability to diverse scenarios. This challenge has fueled the development of more robust and adaptable prompt engineering methodologies, such as the Multi-Agent System for Conditional Mining (MACM) presented in the provided research paper. These recent innovations emphasize the importance of iterative prompt design, and the extraction of core problem components (conditions and objectives) to create more powerful and generalized prompt strategies.
Complex Problem Solving#
The capacity of large language models (LLMs) to effectively solve complex problems, particularly those demanding multi-step reasoning and abstract thought, is a significant area of ongoing research. While LLMs have shown impressive performance on simpler tasks, their capabilities often degrade when faced with intricate, multi-faceted challenges. Prompt engineering, involving techniques like Chain of Thought (CoT), Tree of Thought (ToT), and Graph of Thought (GoT), represents a key approach for improving LLM performance in complex problem-solving scenarios. However, these methods often struggle with generalizability, requiring unique prompt designs for individual problems, and demonstrating only limited success on mathematically challenging problems. Multi-agent systems, like the Multi-Agent System for Condition Mining (MACM) presented in the referenced research paper, offer a potential solution by dynamically generating prompts based on an iterative analysis of problem conditions and objectives. This approach appears to improve both accuracy and generalizability compared to previous methods, highlighting the potential of utilizing agent-based frameworks to address the current limitations in LLM complex problem-solving abilities.
Generalizability and Limits#
The generalizability of novel prompting methods for enhancing Large Language Model (LLM) performance on complex mathematical problems is a crucial consideration. While methods like Tree of Thought (ToT) and Graph of Thought (GoT) demonstrate improved accuracy on specific tasks, their reliance on meticulously crafted, task-specific prompts severely limits their broader applicability. This lack of generalizability arises from the inherent need to manually design prompts tailored to the unique structure and constraints of each problem, hindering their scalability and efficiency for diverse mathematical domains. A key challenge lies in bridging the gap between task-specific prompting engineering and the development of truly generalizable methods. This necessitates a shift towards approaches that can automatically extract relevant problem features and dynamically adapt prompting strategies without explicit human intervention, potentially through techniques such as automated condition mining or learning-based prompt generation. Future research should focus on developing robust methods that are not only effective but also broadly applicable across a wide range of complex mathematical problems. This is crucial for unlocking the full potential of LLMs as powerful tools for mathematical reasoning and problem-solving in various scientific and engineering applications.
Future Research Path#
Future research should focus on enhancing MACM’s efficiency and generalizability. Addressing the computational cost associated with multiple LLM invocations is crucial, perhaps through techniques that optimize the interaction between the Thinker, Judge, and Executor agents. Improving MACM’s performance on geometry problems requires further investigation into how LLMs process spatial reasoning and visual information. Exploring the integration of other advanced prompting methods alongside MACM to further boost performance across various tasks would be beneficial. Finally, extending MACM to other domains beyond mathematics, such as scientific reasoning and code generation, while preserving its inherent strengths, could significantly broaden its impact. A key aspect of future work is expanding the datasets used for evaluation, focusing on more challenging and diverse problems that test the limits of LLM reasoning capabilities. Investigating the robustness of MACM to different LLMs and exploring methods for fine-tuning LLMs specifically for use with MACM are also important considerations for advancing the field.
More visual insights#
More on figures

This figure illustrates the workflow of the Multi-Agent System for Condition Mining (MACM) method. It shows how three agents (Thinker, Judge, Executor) interact to solve complex mathematical problems. The Thinker proposes new conditions, the Judge evaluates their correctness, and the Executor executes the steps to solve the problem if the conditions are sufficient to reach the objective. The process iteratively mines conditions until the objective is achieved, or a predefined limit is reached.

This figure compares MACM with other mainstream prompting methods such as I-O, Few-shot, CoT, SC-CoT, ToT, and GoT. It visually represents the accuracy and universality of each method in solving problems. MACM is highlighted as superior in both aspects, surpassing the others by extracting conditions and objectives iteratively, leading to a solution. The visual representation uses a table format with checkmarks to show the capabilities of each method. MACM stands out with checkmarks in both the Accuracy and Universality columns, indicating its improved performance.

This figure compares MACM with other mainstream prompting methods such as I-O, Few-shot, CoT, SC-CoT, ToT, and GoT. It visually represents the accuracy and universality of each method in solving problems. MACM is shown to improve upon the existing methods by achieving high accuracy and strong generalizability across various mathematical contexts.
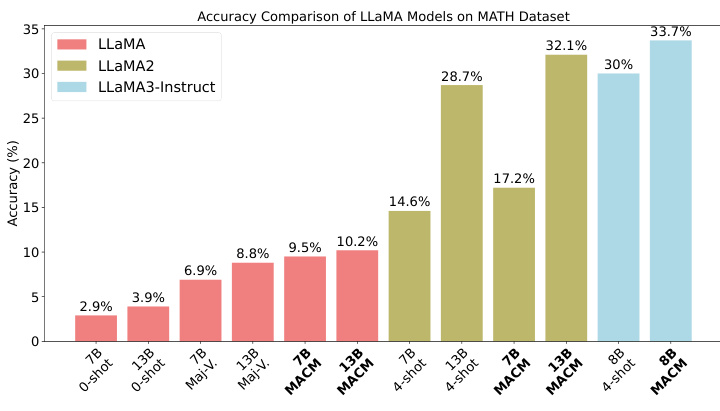
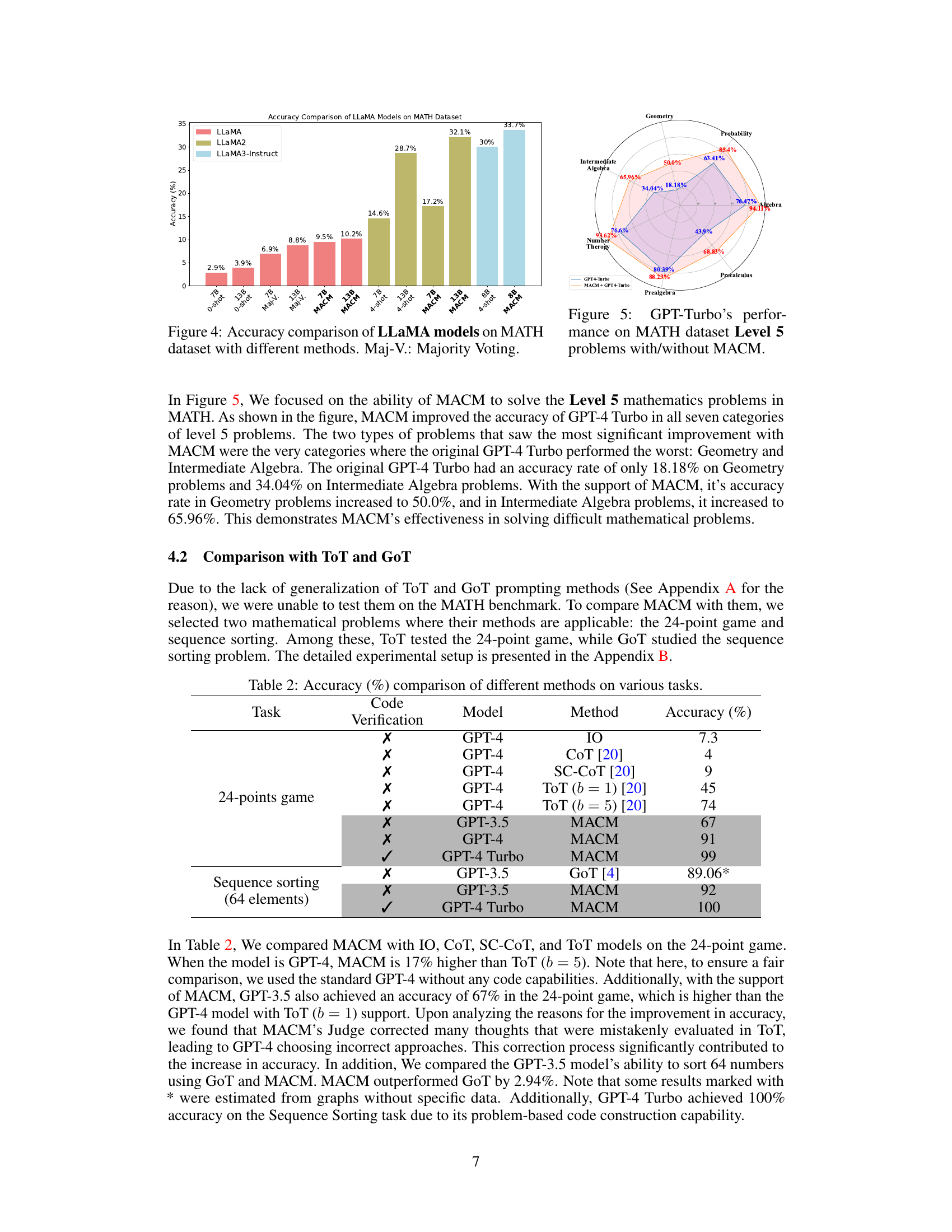
This bar chart compares the accuracy of several LLAMA models (LLaMA, LLaMA2, LLaMA3-Instruct) on the MATH dataset, using different prompting methods. It shows the performance of each model under three conditions: zero-shot, majority voting, and the MACM method, in 7B and 13B parameter sizes. The chart illustrates how MACM improves accuracy across different models and parameter sizes, highlighting its effectiveness.

This radar chart visualizes the performance of GPT-4 Turbo both with and without the MACM prompting method on level 5 problems from the MATH dataset. Each axis represents a different mathematical problem category (Geometry, Probability, Intermediate Algebra, Number Theory, Precalculus, Algebra, Prealgebra). The inner polygon shows the accuracy of GPT-4 Turbo alone, while the outer polygon illustrates the accuracy improvement achieved by incorporating the MACM method. The chart clearly demonstrates MACM’s significant contribution to accuracy across all categories, especially in the areas where GPT-4 Turbo showed weaker performance.
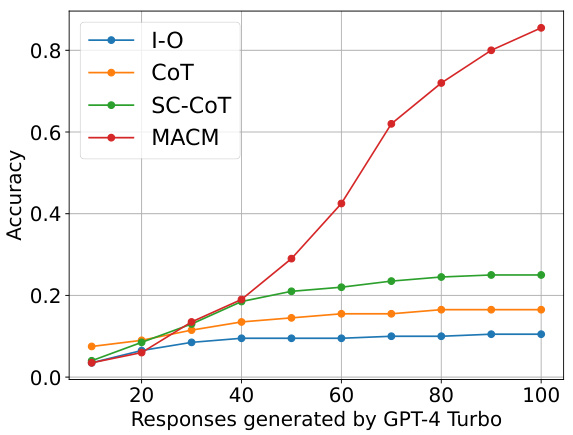
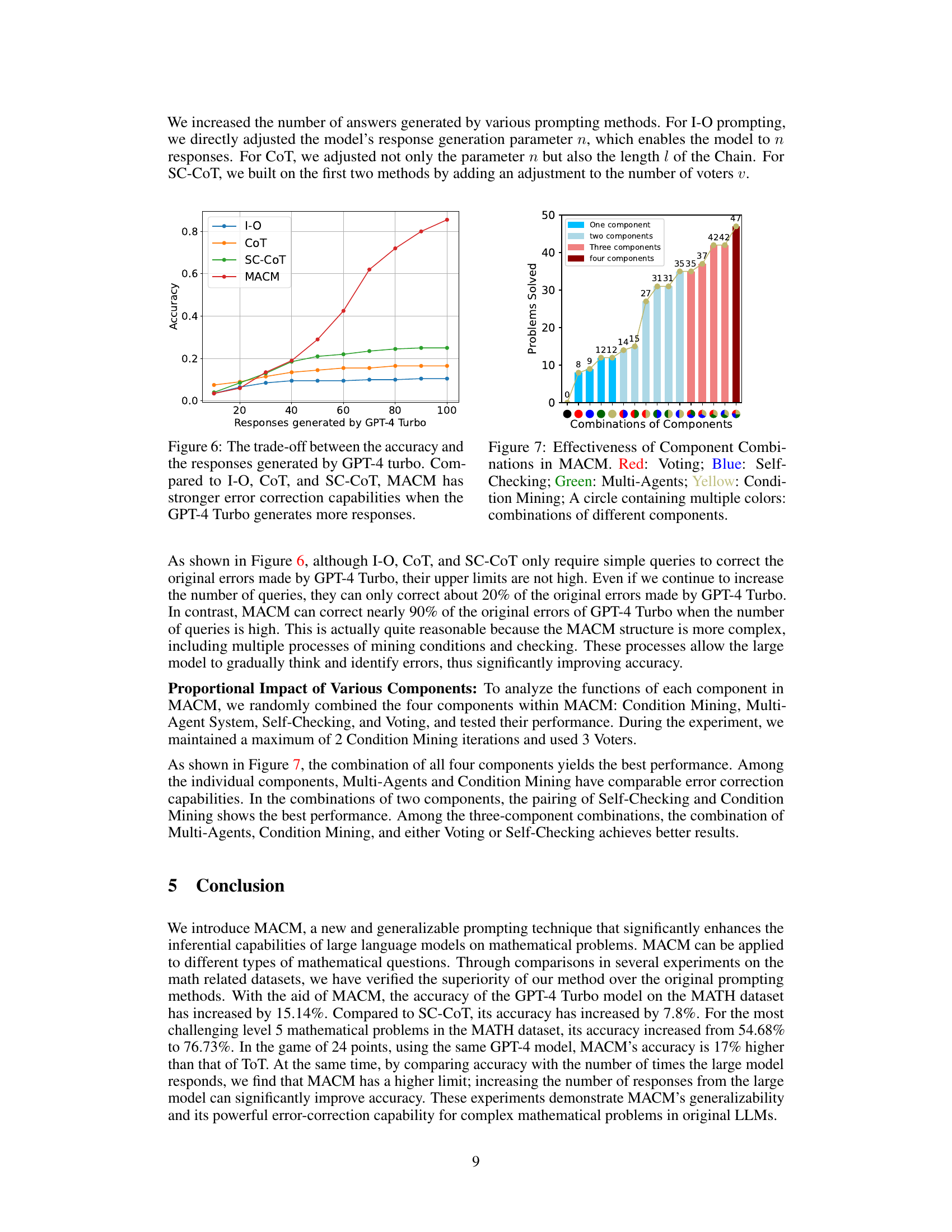
This figure shows the relationship between the accuracy and the number of responses generated by GPT-4 Turbo for different prompting methods: I-O, CoT, SC-CoT, and MACM. It demonstrates that as the number of responses increases, the accuracy of all methods improves, but MACM exhibits a steeper increase and higher accuracy than the others, indicating its superior ability to correct errors with more responses.
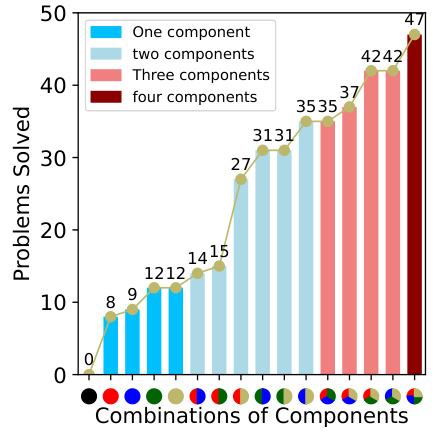
This figure shows the results of an ablation study on the MACM model, investigating the impact of each component on the overall accuracy. The components are: Voting, Self-Checking, Multi-Agents, and Condition Mining. Different combinations of these components were tested, and the number of problems solved is shown for each combination. The figure demonstrates that the combination of all four components yields the best performance, highlighting the synergistic effect of the different components.
More on tables

This table presents the accuracy percentages achieved by the GPT-4 Turbo model on the MATH dataset when using various prompting methods. It compares the performance of the Input-Output (I-O) method, Chain of Thought (CoT), Self-Consistency Chain of Thought (SC-CoT), and the proposed Multi-Agent System for Conditional Mining (MACM) method, as well as results from previous work using the CSV method. The accuracy is broken down by different categories of mathematical problems within the MATH dataset (Algebra, Counting and Probability, Geometry, Intermediate Algebra, Number Theory, Prealgebra, and Precalculus).
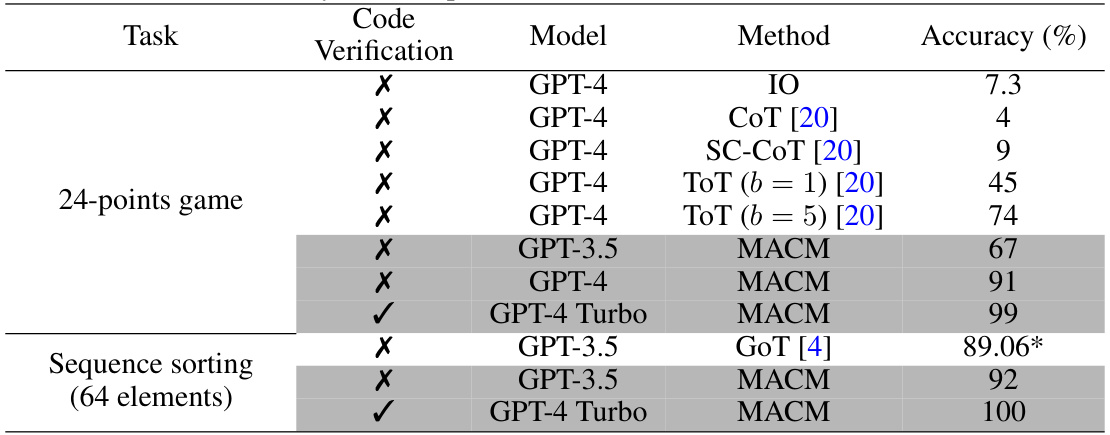
This table compares the accuracy of various prompting methods (I-O, CoT, SC-CoT, ToT, GoT, and MACM) on two specific tasks: the 24-points game and sequence sorting (with 64 elements). It shows the model used (GPT-3.5, GPT-4, GPT-4 Turbo), whether code verification was used, and the resulting accuracy percentage. Note that the GoT accuracy for sequence sorting is marked with an asterisk, indicating it may be an estimate from a graph rather than a precise value.

This table presents the accuracy of GPT-4 Turbo on the MATH dataset using various prompting methods, including I-O, CoT, SC-CoT, and MACM. It shows the accuracy across different subcategories of math problems within the MATH dataset (Algebra, Counting and Probability, Geometry, Intermediate Algebra, Number Theory, Prealgebra, and Precalculus). The results demonstrate the performance improvement achieved by MACM compared to the baseline and other prompting methods.
Full paper#