↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Traditional link prediction methods struggle with dynamic data and the exploitation-exploration dilemma. Existing approaches often rely on static datasets and lack theoretical performance guarantees. This limits their ability to adapt to evolving user preferences and to effectively balance exploration (discovering new links) and exploitation (using existing knowledge). The inherent challenge is that prioritizing popular items may prevent the discovery of new, potentially valuable links.
To overcome this, the paper introduces PageRank Bandits (PRB), a novel algorithm that combines the strengths of contextual bandits and PageRank. PRB addresses the exploitation-exploration dilemma using a contextual bandit framework while also leveraging the power of PageRank for incorporating graph structure. Extensive experiments on real-world datasets demonstrate the superiority of PRB compared to existing methods, particularly in handling dynamic data and achieving effective exploitation-exploration.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on link prediction and sequential decision-making in graph learning. It provides a novel fusion algorithm, bridges the gap between bandit algorithms and graph-based methods, and offers a theoretical performance guarantee, paving the way for more effective and adaptable link prediction systems. The empirical evaluation on diverse datasets demonstrates its superiority over existing state-of-the-art methods, opening new avenues for further research in dynamic graph environments and addressing the exploitation-exploration dilemma.
Visual Insights#
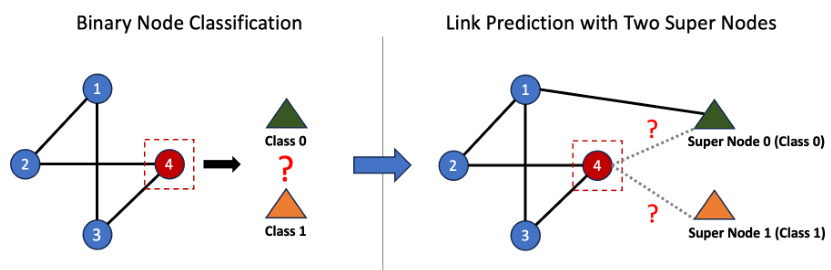
The figure illustrates how a binary node classification problem can be converted into a link prediction problem. A node classification task aims to assign a node to one of two classes (0 or 1). This is transformed into a link prediction task by adding two ‘supernodes’, one for each class. Then, the task becomes predicting whether a link exists between the original node and each supernode. The reward is 1 if the link prediction is correct (the node belongs to the class of the supernode it is linked to); otherwise, it is 0.
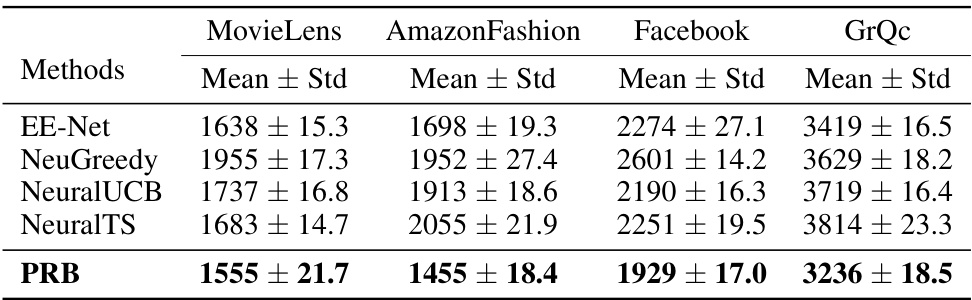
This table presents the cumulative regret values achieved by various bandit-based methods (EE-Net, NeuGreedy, NeuralUCB, NeuralTS, and PRB) on four different online link prediction datasets (MovieLens, AmazonFashion, Facebook, and GrQc). Lower cumulative regret indicates better performance. The results demonstrate the performance of the proposed method (PRB) compared to the baseline methods. The mean and standard deviation of cumulative regret across 10 runs are reported for each method.
In-depth insights#
PRB Algorithm#
The PRB (PageRank Bandits) algorithm represents a novel fusion of contextual bandit methods and PageRank, addressing the exploration-exploitation dilemma inherent in link prediction. Its core innovation lies in using PageRank to propagate and leverage graph structural information, enhancing both exploration (discovering new links) and exploitation (leveraging known links) strategies. By integrating a contextual bandit framework, PRB models link prediction as a sequential decision-making process. This allows it to adapt to dynamic graph structures and evolving node contexts, a key advantage over traditional supervised learning approaches. A unique reward formulation is introduced, along with a theoretical analysis demonstrating sub-linear regret growth. Empirical evaluations show that PRB outperforms existing bandit and graph-based methods across various datasets, demonstrating the effectiveness of this fusion approach. The algorithm’s adaptability, theoretical grounding, and strong empirical results make it a significant contribution to the field of link prediction.
Regret Analysis#
A regret analysis in a machine learning context, particularly within the framework of contextual bandits, is crucial for evaluating the performance of a learning algorithm over time. It quantifies the difference between the cumulative reward achieved by the algorithm and the optimal reward achievable with perfect knowledge. The analysis typically involves deriving an upper bound on the cumulative regret. This bound helps to characterize the algorithm’s efficiency and convergence rate, showing how the regret grows as a function of the number of interactions or time steps. A sub-linear regret bound is highly desirable, indicating that the algorithm’s performance approaches optimality over time. The analysis often relies on assumptions about the reward function, such as linearity or boundedness, and the problem’s structure, and may consider various complexity measures, such as the dimensionality of the context space. The choice of reward function, the impact of exploration-exploitation strategies, and the consideration of graph structure or other contextual information are all critical elements in a comprehensive regret analysis. The ultimate goal is to provide theoretical guarantees on the algorithm’s performance, enabling informed comparisons and choices among different algorithms.
Empirical Results#
An Empirical Results section in a research paper should present a thorough evaluation of the proposed approach. Quantitative results, such as precision, recall, F1-score, or AUC, should be reported across multiple datasets and compared against relevant baselines. The discussion should extend beyond simply stating the numbers; it must interpret the findings, addressing whether the results meet the expectations established in the theoretical analysis (if any). Statistical significance must be carefully considered, with appropriate measures used to demonstrate the reliability of the observed performance differences. Furthermore, the discussion should acknowledge any limitations of the experimental setup or potential sources of bias. A robust empirical evaluation builds confidence in the proposed method’s generalizability and practical value. Qualitative insights may also enrich the section, providing contextual understanding of the method’s strengths and weaknesses in specific scenarios.
Future Work#
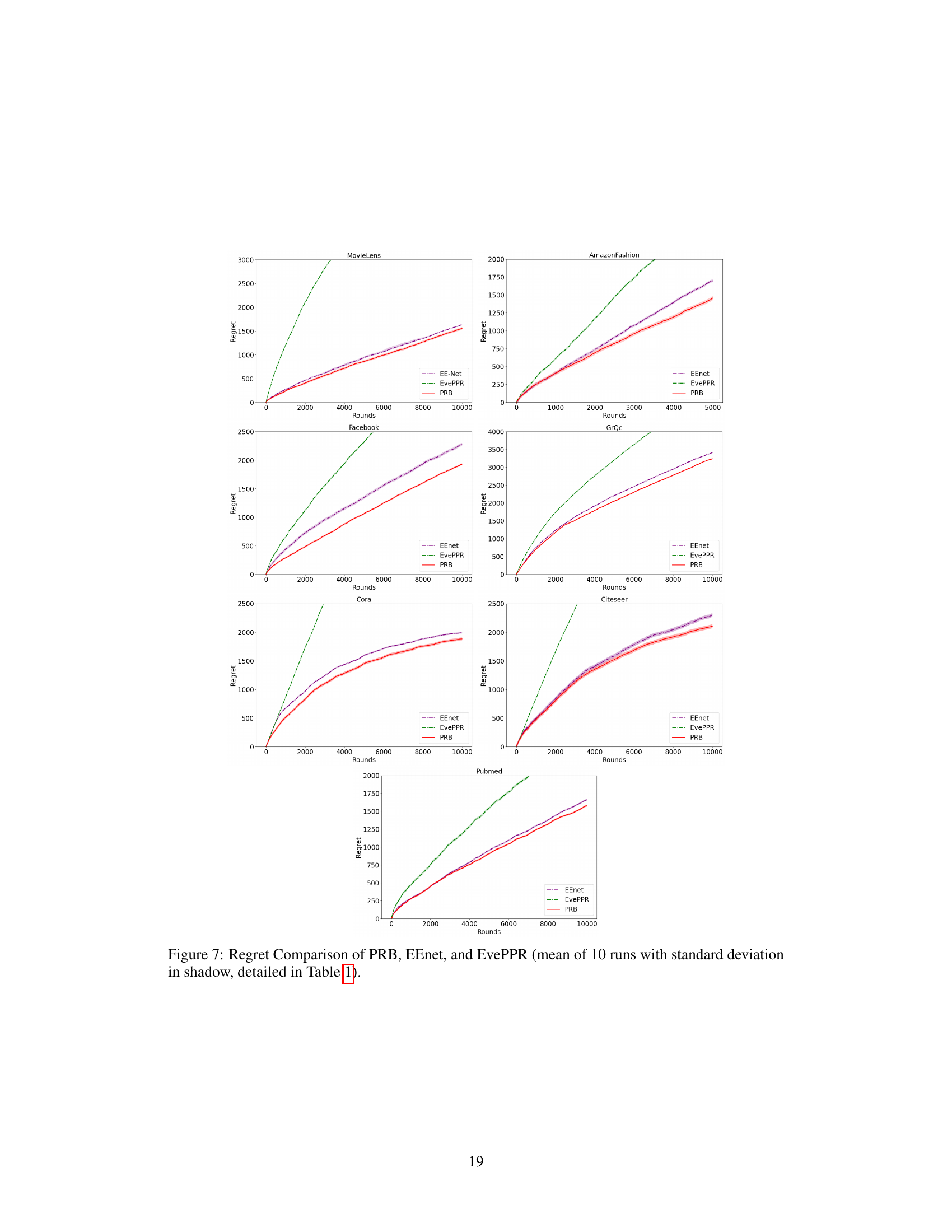
Future research directions stemming from this PageRank Bandits (PRB) paper could involve several key areas. Extending PRB to dynamic graphs is crucial, as real-world networks constantly evolve. This would necessitate adapting the PageRank and bandit components to handle edge insertions and deletions efficiently. Developing more sophisticated reward functions is another avenue. The current binary reward could be enriched to reflect various aspects of link quality (e.g., interaction time, content relevance), improving accuracy and interpretability. Investigating alternative bandit algorithms beyond UCB and Thompson Sampling is warranted to explore the potential for even better exploitation-exploration balances. Finally, a comprehensive theoretical analysis of PRB’s performance under various graph properties (e.g., density, community structure) would strengthen the foundation and lead to optimized strategies for real-world applications. This includes exploring more powerful exploration strategies and different reward functions for superior performance.
Limitations#
A thoughtful analysis of the ‘Limitations’ section of a research paper would delve into the methodological constraints, acknowledging any simplifying assumptions made for tractability. It should discuss the scope and generalizability of the findings, emphasizing the extent to which conclusions can be reliably extrapolated beyond the specific datasets or experimental conditions used. A critical discussion of potential biases in data collection, model selection, or evaluation metrics is also crucial, acknowledging the impact these might have on the validity of results. Furthermore, the discussion should address any computational limitations, noting the scalability and efficiency of the proposed methods, while considering the resource requirements for reproduction and deployment. Finally, future directions for improving the approach or addressing these limitations should be suggested.
More visual insights#
More on figures

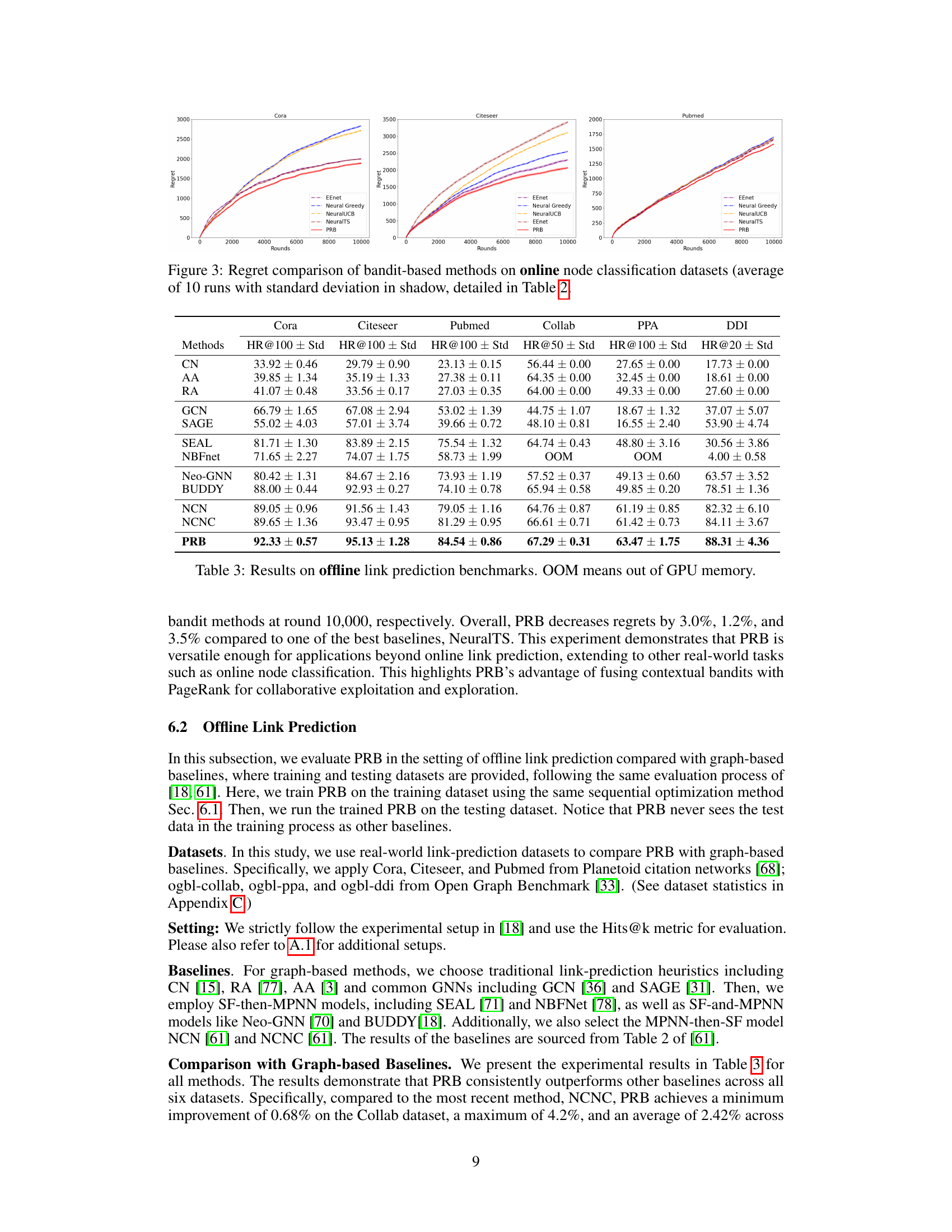
The figure compares the cumulative regret of five different bandit-based methods for online link prediction across four datasets: MovieLens, AmazonFashion, Facebook, and GrQc. The x-axis represents the number of rounds, and the y-axis represents the cumulative regret. Each line represents a different algorithm: EE-Net, NeuralGreedy, NeuralUCB, NeuralTS, and PRB. The shaded area around each line indicates the standard deviation across 10 runs. The figure shows that PRB consistently outperforms the other methods across all datasets.
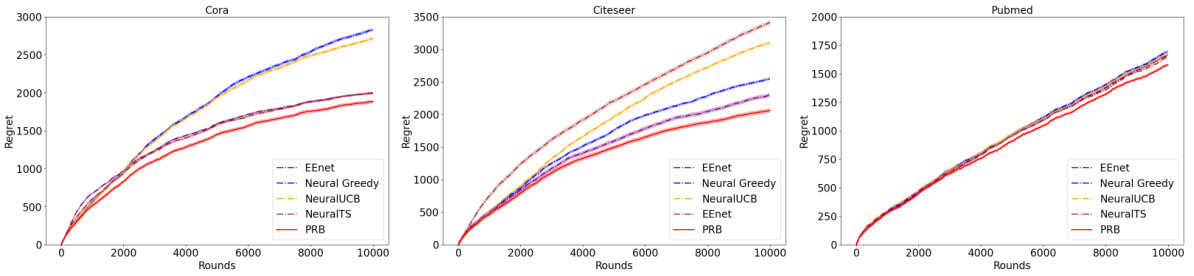
This figure compares the cumulative regret of several bandit-based algorithms (EE-Net, Neural Greedy, NeuralUCB, NeuralTS, and PRB) on three node classification datasets (Cora, Citeseer, and Pubmed). The x-axis represents the number of rounds, while the y-axis shows the cumulative regret. Each line represents the performance of a different algorithm on a specific dataset. The figure visually demonstrates PRB’s superior performance in terms of minimizing cumulative regret compared to the other algorithms across all datasets.
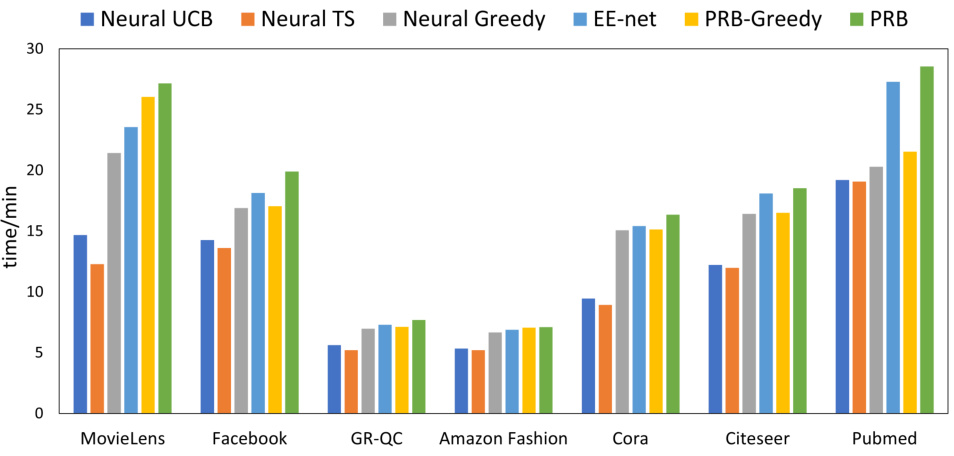
This figure compares the running time of the proposed algorithm PRB with several bandit-based baselines (Neural UCB, Neural TS, Neural Greedy, EE-net, PRB-Greedy) across eight datasets (MovieLens, Facebook, GR-QC, Amazon Fashion, Cora, Citeseer, Pubmed). The running time is measured in minutes. The datasets represent various types of graphs, including recommendation networks and citation networks. The figure shows that the running time of PRB is generally comparable to that of other baselines. This suggests that the computational cost of PRB is not prohibitively high and that it is a practical algorithm for link prediction.

This figure shows a bar chart comparing the proportion of running time spent on exploitation-exploration versus random walk for both PRB-Greedy (a simplified version of PRB without the exploration network) and PRB (the full algorithm). The chart is broken down by dataset, allowing for a comparison across different graph structures and sizes. It visually represents the computational trade-off inherent in the algorithms: the proportion of time dedicated to the random walk step (a crucial part of PageRank integration in PRB) relative to the time for the core exploitation and exploration components.

This figure compares the performance of several bandit-based methods for online link prediction on four different datasets: MovieLens, AmazonFashion, Facebook, and GrQc. The cumulative regret is plotted against the number of rounds. Lower regret indicates better performance. The figure shows that PRB consistently outperforms other methods across all datasets. The shaded areas represent the standard deviation across 10 runs for each method. More detail on the quantitative results can be found in Table 1.
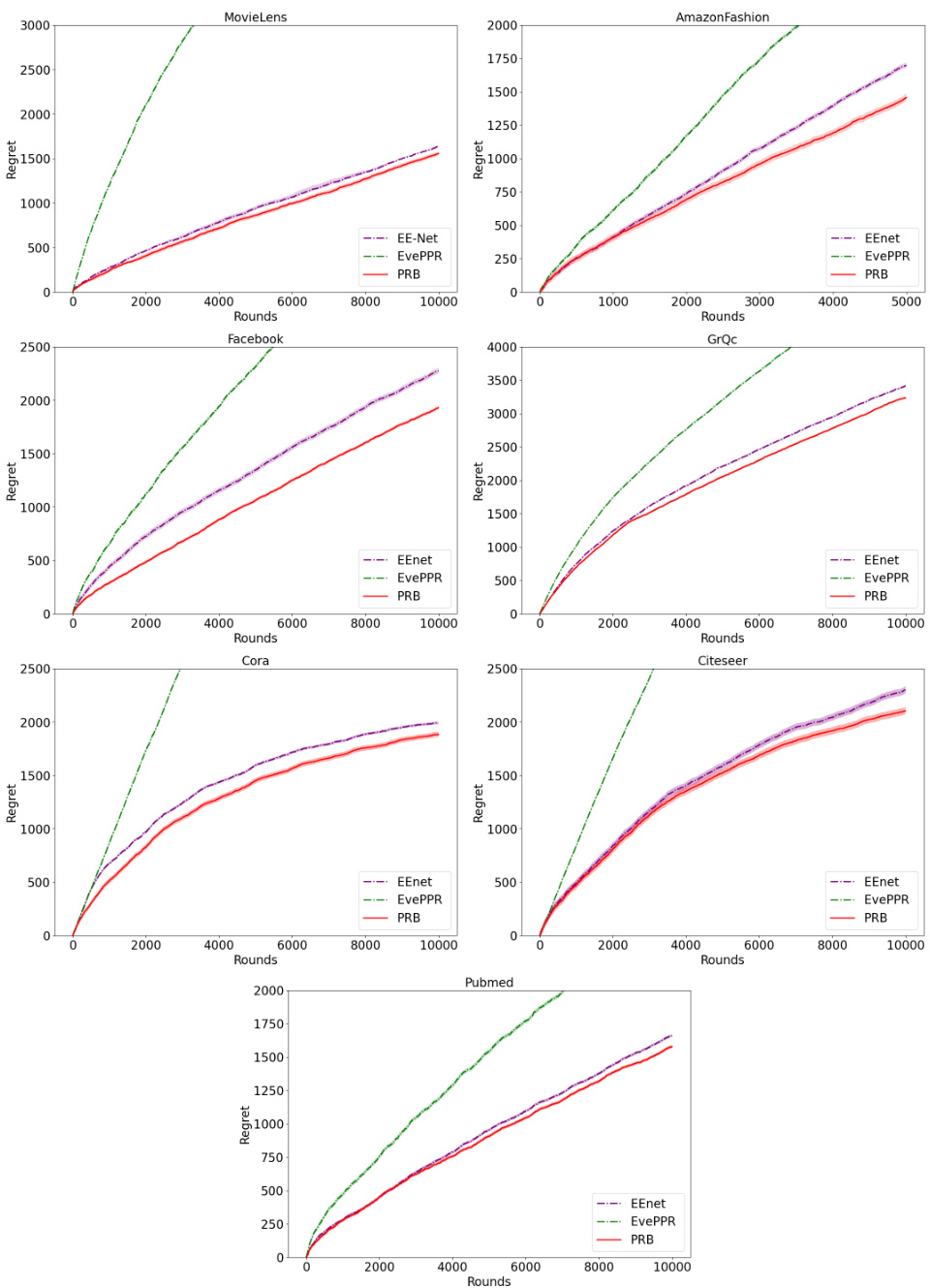
This figure compares the cumulative regret of several bandit-based methods for online link prediction across four different datasets: MovieLens, AmazonFashion, Facebook, and GrQc. The x-axis represents the number of rounds, and the y-axis represents the cumulative regret. Each line represents a different method, showing their performance over time. The shaded area around each line indicates the standard deviation across 10 runs, providing a measure of variability in performance. Table 1 provides the detailed numerical results shown graphically in this figure.
More on tables
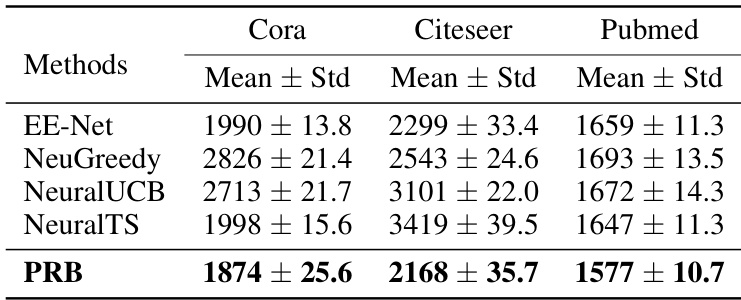
This table presents the cumulative regret results for various bandit-based methods (EE-Net, NeuGreedy, NeuralUCB, NeuralTS) and the proposed PRB method on three online node classification datasets (Cora, Citeseer, and Pubmed). The lower the cumulative regret, the better the performance of the method. The mean and standard deviation of the cumulative regret are shown for each method across multiple runs.
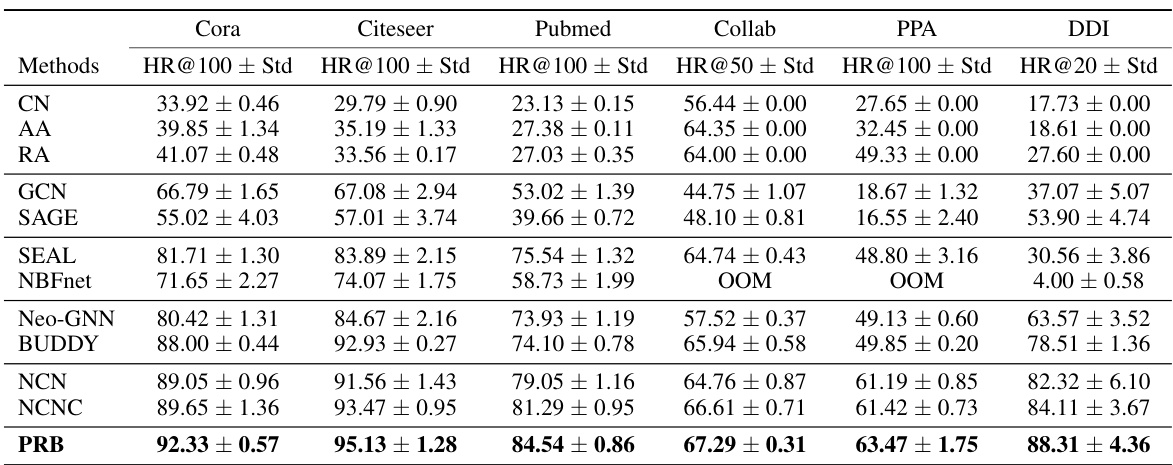
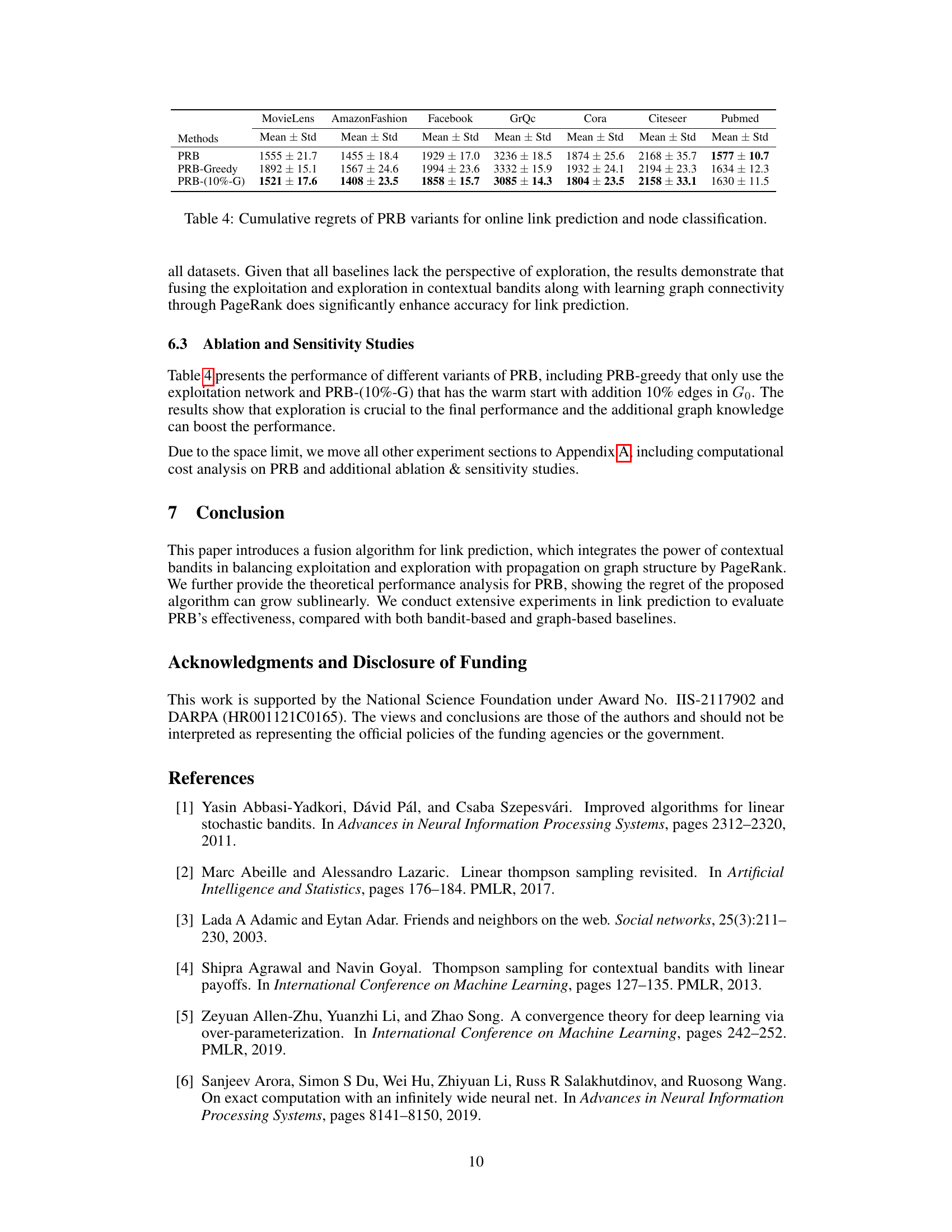
This table presents the results of offline link prediction experiments comparing PRB against several graph-based baselines across six datasets. The results are reported using the Hits@k metric. The table shows that PRB achieves consistently better performance than all other methods across all datasets. OOM denotes that the method ran out of GPU memory.

This table presents the cumulative regret of various bandit-based methods (EE-Net, NeuGreedy, NeuralUCB, NeuralTS, and PRB) on four different online link prediction datasets (MovieLens, AmazonFashion, Facebook, and GrQc). The cumulative regret is a measure of the algorithm’s performance, with lower values indicating better performance. The results show PRB’s consistent outperformance of other methods across all datasets.
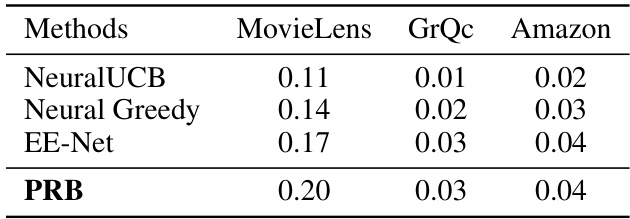
This table presents the cumulative regret of several bandit-based methods for online link prediction on four datasets: MovieLens, Amazon Fashion, Facebook, and GrQc. The methods compared include EE-Net, NeuGreedy, NeuralUCB, NeuralTS, and PRB. Lower values indicate better performance, reflecting a smaller cumulative difference between the algorithm’s choices and those of an optimal predictor. The standard deviation is also provided.

This table presents the results of offline link prediction experiments, comparing the proposed PRB method against several graph-based baselines across six datasets. The results are measured using the Hits@100 metric, which represents the accuracy of link prediction. The table shows that PRB generally outperforms the existing methods, particularly on the Collab, PPA, and DDI datasets. OOM indicates that a method ran out of GPU memory and thus could not complete the experiment.

This table presents the cumulative regret values achieved by different bandit-based methods (EE-Net, NeuGreedy, NeuralUCB, NeuralTS, and PRB) on four online link prediction datasets (MovieLens, AmazonFashion, Facebook, and GrQc). The cumulative regret is a metric that evaluates the algorithm’s performance in sequentially making link predictions and aims to measure how far the algorithm’s performance is from the optimal strategy. A lower cumulative regret indicates better performance.
Full paper#