↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many existing approaches for solving inverse problems using diffusion models are limited by their instability and amplified cumulative errors, especially when dealing with real-world, complex data. These models often rely on simplified linear representations and overlook the impact of measurement quality and the unreliable nature of priors. This research highlights the critical role of Temporal Distribution Discrepancy in explaining this instability and limits of existing methods.
To address the shortcomings of previous methods, this paper proposes a novel score-based diffusion framework called Dynamics-aware SDE Diffusion Generative Model (D³GM). D³GM leverages the measure-preserving dynamics of Random Dynamical Systems to enhance the stability and generalizability of the model, making it robust to various forms of degradation, noise and domain shift. The experimental results corroborate the efficacy of D³GM across multiple benchmarks, including magnetic resonance imaging, showcasing its ability to deliver high-quality restorations even under challenging circumstances.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on inverse problems and diffusion models. It addresses a critical gap in understanding the limitations of current approaches and proposes a novel framework (D³GM) that significantly improves the stability and generalizability of diffusion models for solving these challenging problems. The theoretical framework using RDS and the experimental results on various benchmarks make it particularly relevant to researchers focused on image restoration and generation using SDEs.
Visual Insights#

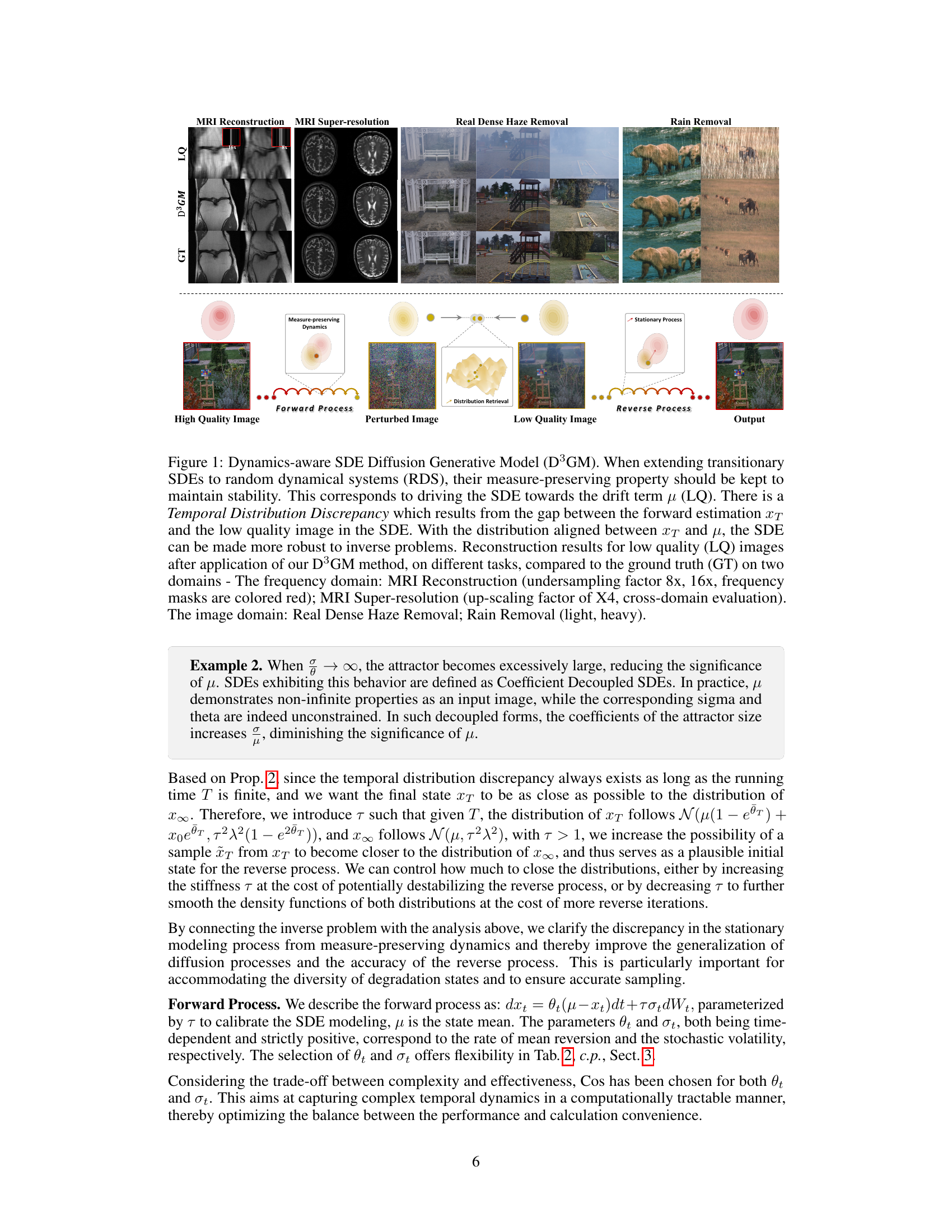
This figure shows the architecture of the proposed Dynamics-aware SDE Diffusion Generative Model (D³GM) and its application to various image restoration tasks. It highlights the measure-preserving property of the model and how it addresses the temporal distribution discrepancy issue in solving inverse problems. The figure presents qualitative results on MRI reconstruction, MRI super-resolution, haze removal, and rain removal, demonstrating the effectiveness of D³GM across different domains and complexities.

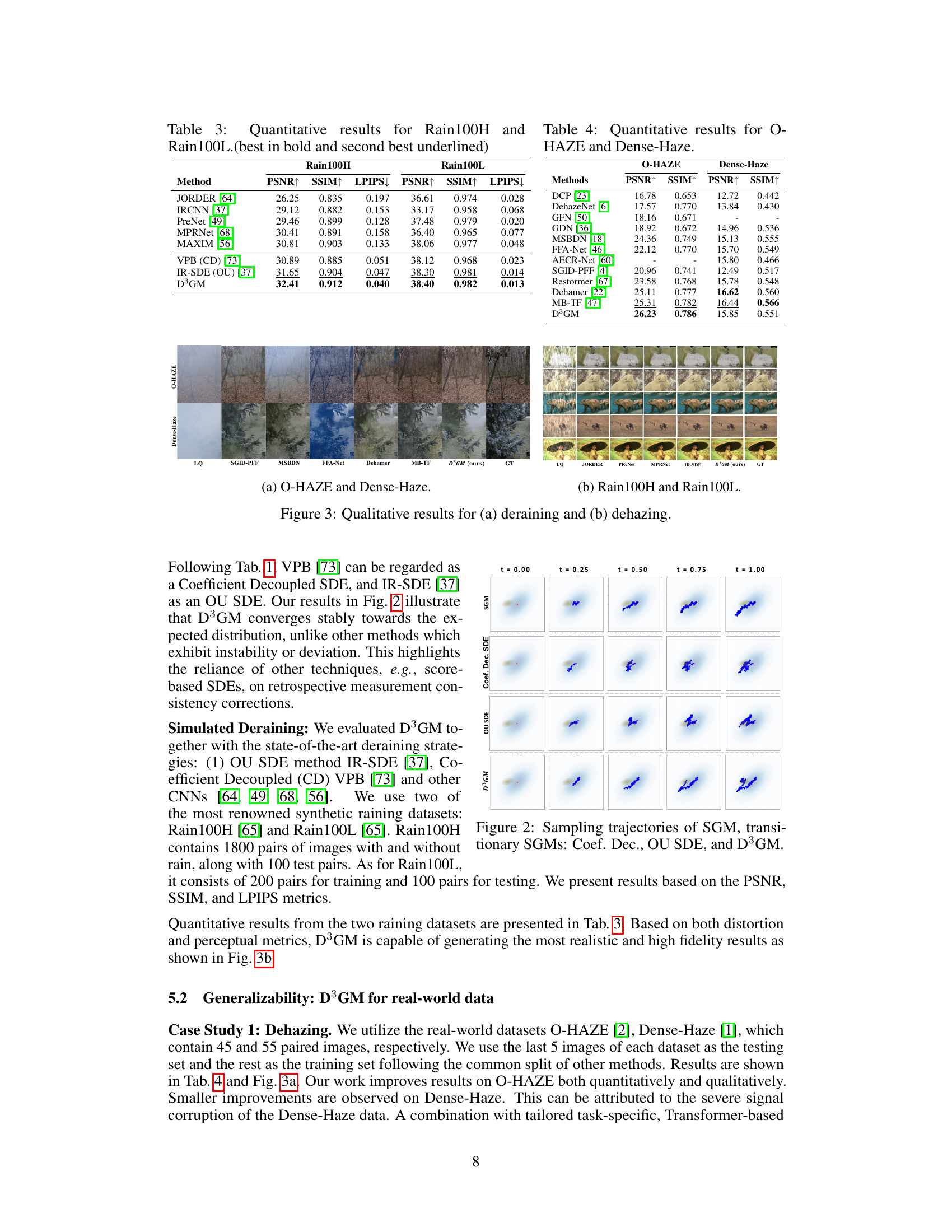
This table compares four different state-of-the-art SDE diffusion-based approaches for solving inverse problems. It shows the prior distribution used for X0 (initial state) and X1 (final state), the theoretical foundation of each approach, their key properties (stability, handling of prior knowledge), Temporal Distribution Discrepancy (TDD) characteristics, the type of attractor in their underlying dynamical systems, the type of operator they are suitable for (linear or non-linear), and whether they are suitable for one-sided or two-sided inverse problems.
In-depth insights#
SDE Stability#
The stability of Stochastic Differential Equations (SDEs) in the context of diffusion models is crucial for reliable performance. Instability in SDEs can lead to accumulated errors, hindering the generation of high-quality samples and the effective solution of inverse problems. The paper analyzes this instability through the lens of measure-preserving dynamics, uncovering how the failure to preserve the measure throughout the diffusion process results in Temporal Distribution Discrepancy. This discrepancy amplifies the impact of noise and errors at each step, significantly affecting the model’s ability to return to the original state during the reverse process. The authors demonstrate how maintaining measure-preserving dynamics using techniques like Random Dynamical Systems (RDS) enhances the stability and generalizability of diffusion models, and propose a novel framework that achieves a robust and reliable solution by controlling the Temporal Distribution Discrepancy. This is achieved by using a measure-preserving strategy which effectively mitigate the influence of accumulated errors and degradation during both the forward and reverse diffusion process. In essence, the paper establishes a clear theoretical foundation for understanding and addressing SDE stability issues in diffusion models, impacting the reliability and performance of these models across various applications.
DGM Framework#
The Dynamics-aware SDE Diffusion Generative Model (DGM) framework offers a novel approach to enhancing the stability and generalizability of diffusion models for inverse problems. It addresses limitations of existing methods by incorporating measure-preserving dynamics from random dynamical systems (RDS). This crucial aspect ensures that the model maintains stability even under complex degradations, mitigating the accumulation of errors. By incorporating the measure-preserving property, the DGM can effectively recover the original state from degraded measurements. The framework introduces Temporal Distribution Discrepancy as a key concept for analyzing stability. Furthermore, it leverages a stationary process to ensure robust performance across diverse benchmarks and challenging settings. The DGM framework represents a significant theoretical contribution, providing a more rigorous foundation for score-based diffusion models, and promises a powerful enhancement in solving various inverse problems.
RDS Dynamics#
The concept of ‘RDS Dynamics,’ likely referring to Random Dynamical Systems dynamics, is crucial for enhancing the stability and generalizability of diffusion models in solving inverse problems. RDS provides a framework for analyzing the temporal evolution of probability distributions under complex transformations, such as those encountered in image degradation. By leveraging the measure-preserving property of RDS, the approach aims to mitigate the accumulation of errors inherent in iterative processes. This is achieved by ensuring the model’s ability to return to an original state even after significant degradation. The analysis of Temporal Distribution Discrepancy highlights a key instability issue in existing methods, which RDS dynamics addresses by providing a more robust and theoretically grounded approach. The core idea is to guide the diffusion process toward a stationary measure, maintaining stability despite complex degradations. This measure-preserving property is essential for ensuring reliable and consistent results, especially when dealing with noisy or incomplete data frequently encountered in real-world inverse problems.
Inverse Problems#
Inverse problems, focused on estimating causal factors from observational data, are inherently ill-posed due to the complexity of mapping incomplete or degraded data to parameters. This ill-posed nature necessitates iterative, data-driven solutions, especially prevalent in image reconstruction from noisy signals. Diffusion models offer a promising approach, leveraging their superior reconstruction capabilities and compatibility with iterative solvers. However, existing methods often simplify inverse problems by assuming linearity, limiting their effectiveness for complex real-world applications. The reliance on linear stochastic differential equations (SDEs) neglects the crucial aspect of measure-preserving dynamics, leading to accumulated errors and biases. A deeper understanding of the measure-preserving dynamics of random dynamical systems (RDS), through the lens of temporal distribution discrepancy, is crucial for developing robust and generalizable diffusion models for diverse, challenging inverse problems.
Future Works#
Future research directions stemming from this work could explore extending the D³GM framework to handle even more complex degradation scenarios, such as those involving both unknown and heterogeneous degradation. A second avenue would involve investigating the theoretical limits of the measure-preserving dynamics approach, potentially developing more refined bounds on model error and exploring alternative mathematical frameworks for enhancing stability and generalizability. Finally, a deeper investigation into the interplay between the choice of noise schedule and the stability of the diffusion process could lead to more efficient and robust training methods. Specifically, exploring alternative noise schedules tailored to complex real-world degradations and establishing a principled way to select the optimal schedule based on the properties of the degradation would be valuable. Furthermore, evaluating D³GM on a wider variety of inverse problems and high-dimensional data modalities would further establish its generalizability and practicality.
More visual insights#
More on figures

This figure illustrates the proposed Dynamics-aware SDE Diffusion Generative Model (D³GM) for solving inverse problems. It highlights the importance of measure-preserving dynamics in maintaining stability during the diffusion process and addresses the issue of temporal distribution discrepancy. The figure shows the architecture of D³GM, which involves a forward and reverse process. The model is applied to various tasks including MRI reconstruction, MRI super-resolution, real dense haze removal, and rain removal, with reconstruction results shown for each task. These results are compared to the ground truth, demonstrating the effectiveness of D³GM in restoring high-quality images from degraded inputs.

This figure displays sampling trajectories of different SDE diffusion models over time. It visually demonstrates the stability and instability of various approaches. The top row shows the sampling trajectory of a standard Score-based Generative Model (SGM). The middle rows showcase transitionary SGMs, specifically, a Coefficient Decoupled SDE (Coef. Dec. SDE) and an Ornstein-Uhlenbeck SDE (OU SDE). The bottom row illustrates the sampling trajectory of the proposed Dynamics-aware SDE Diffusion Generative Model (D³GM). By comparing the trajectories across different models, the figure highlights the stability and generalizability advantages of the D³GM in handling challenging inverse problems. The instability of other models is evidenced by their failure to consistently converge towards the target distribution.

This figure illustrates the concept of reverse initialization and its relation to the basin of attraction in the context of the proposed diffusion model. The left side shows a schematic of the forward and reverse diffusion processes. The forward process (red arrow) maps the high-quality image (x₀) to the low-quality observation (y) through the operator A. The reverse process (brown arrow) aims to recover x₀ from y. The dotted oval represents the basin of attraction around the true high-quality image (x₀). The right-hand side provides a visual interpretation in a three-dimensional space. Each curve represents the probability distribution at a different time step. As the reverse process progresses (indicated by the red arrows), the distribution shifts from being spread out around y to being concentrated around the actual image (x₀). The success of the reverse process depends on whether it starts in the basin of attraction (as shown). Starting far outside the basin of attraction can lead to the diffusion process converging to a point other than x₀.

This figure displays qualitative comparison results for deraining and dehazing tasks. It shows low-quality (LQ) images, images processed by the Dynamics-aware SDE Diffusion Generative Model (D³GM), and ground truth (GT) high-quality images side-by-side for various examples in each task, demonstrating the visual quality improvement achieved by the proposed method.

This figure displays the deraining results of the proposed D³GM method on images with heavy rain. It shows three columns: the first shows the low-quality (LQ) images with heavy rain streaks, the second shows the images after deraining with D³GM, and the third shows the ground truth (GT) images. The results demonstrate the ability of the D³GM model to effectively remove rain streaks while preserving image details and quality.

This figure showcases the performance of the D³GM model on real-world hazy images. It presents three columns: the first shows the low-quality (LQ) hazy input images, the second displays the images restored by the D³GM model (D³GM (ours)), and the third shows the corresponding ground truth (GT) images. The results demonstrate the model’s ability to effectively remove haze from real-world images, preserving details and improving visual quality.

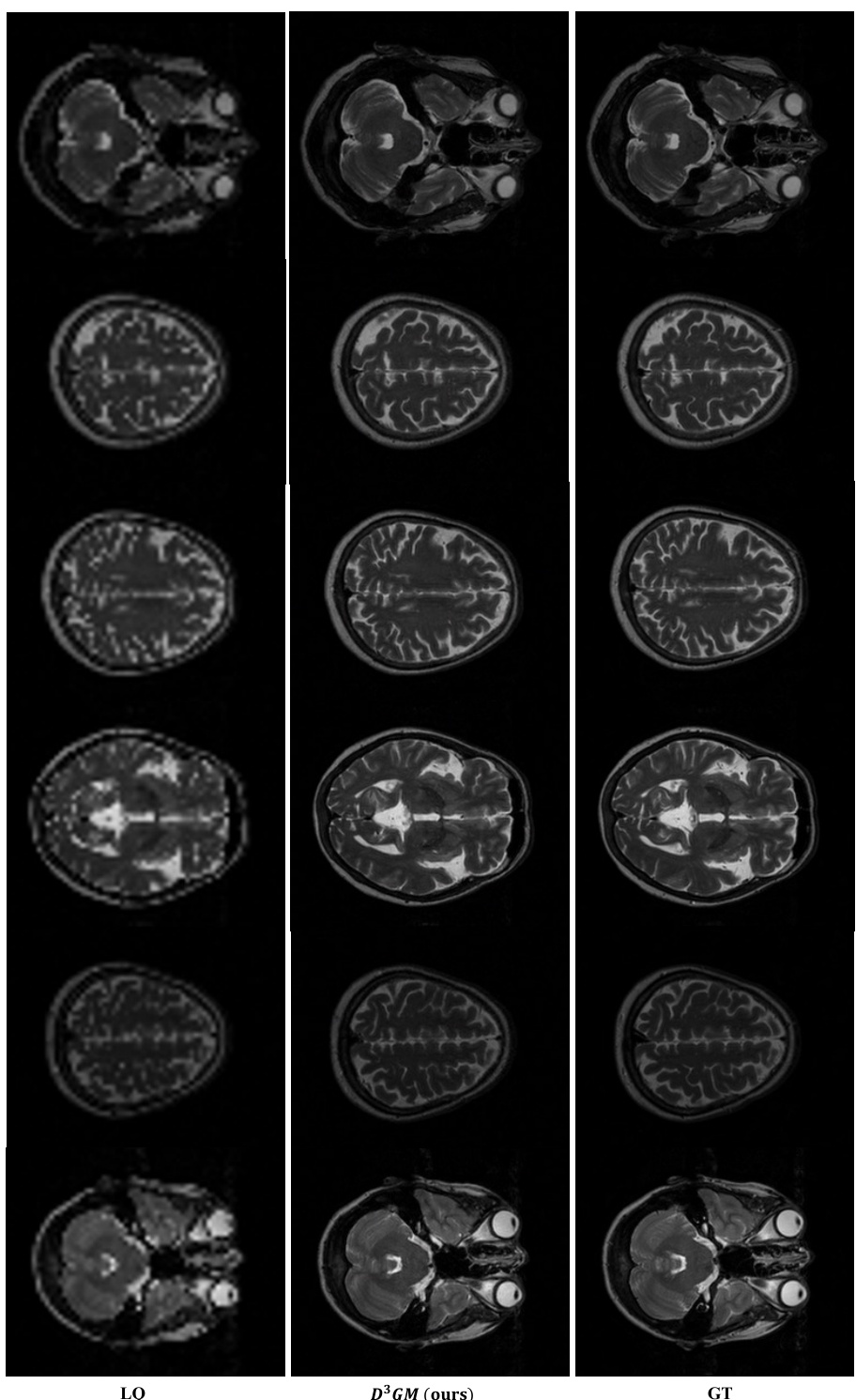
This figure shows the MRI reconstruction results obtained using the proposed D³GM method compared to the ground truth (GT) and low-quality (LQ) images. The results are presented for two different undersampling rates (8x and 16x) and two encoding directions (Frequency-encoding and Phase-encoding). It illustrates the model’s performance in reconstructing MRI images from undersampled k-space data, highlighting its effectiveness in handling different undersampling levels and encoding schemes.
This figure displays the results of MRI super-resolution using the proposed D³GM method. It shows the low-quality (LQ) input images, the results produced by D³GM, and the ground truth (GT) images. The images are arranged in columns, with each column representing a different sample. This visualization allows for a qualitative assessment of the model’s performance on in-domain data.

This figure shows the architecture of the proposed Dynamics-aware SDE Diffusion Generative Model (D³GM) and illustrates its application to various image restoration tasks. The left side shows the overall framework with the forward and reverse processes using measure-preserving dynamics to enhance stability. The right side presents qualitative results of D³GM on four different tasks: MRI reconstruction (with 8x and 16x undersampling), MRI super-resolution (4x upscaling), real dense haze removal and rain removal, demonstrating its effectiveness across diverse image restoration problems.

This figure shows the results of MRI reconstruction using the proposed D³GM method. Two different undersampling rates (8x and 16x) were used, and results are displayed for both frequency-encoding and phase-encoding directions. For each undersampling rate and direction, the low-quality (LQ) input image, the reconstruction result from D³GM, and the ground truth (GT) are shown side-by-side for comparison. This visualization helps to illustrate the performance of D³GM across different undersampling scenarios and encoding directions, demonstrating its ability to reconstruct high-quality images from undersampled data.
More on tables
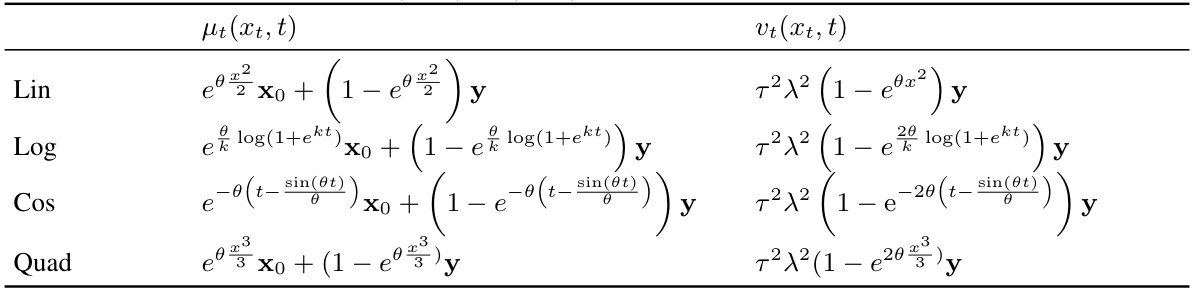
This table compares four different SDE diffusion-based approaches: SGM, IR-SDE, I2SB, and the proposed D³GM. It highlights key differences in their prior distributions (p(X0), p(X1)), theoretical foundations, properties, and whether they are suitable for linear, nonlinear, or blind inverse problems. D³GM is shown to improve on stability and robustness compared to existing methods.

This table presents the quantitative results of the fastMRI dataset using different acceleration rates (x8 and x16). The performance of various methods, including ZeroFilling, D5C5, DAGAN, SwinMR, DiffuseRecon, CDiffMR, and the proposed D³GM, is evaluated using PSNR, SSIM, and LPIPS metrics. Higher PSNR and SSIM values, and lower LPIPS values indicate better image reconstruction quality.
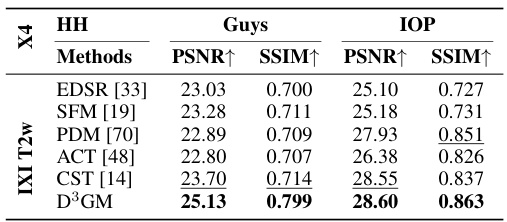
This table presents the quantitative results of MRI super-resolution (SR) experiments conducted on the IXI dataset. It specifically focuses on the performance of various methods on unseen datasets, showcasing the generalizability and robustness of the approaches across different domains and acquisition parameters. The table includes PSNR and SSIM scores, which are common image quality metrics, for multiple methods, including the proposed D³GM model, on three different datasets (HH, Guys, and IOP). Higher scores indicate better performance. The ‘unseen datasets’ aspect highlights the importance of the cross-domain generalization capabilities assessed.

This table compares the performance of the proposed D³GM model against other state-of-the-art deraining methods on the rain200H dataset. The metrics used for comparison are PSNR (Peak Signal-to-Noise Ratio), SSIM (Structural Similarity Index), the number of parameters, and FLOPs (floating point operations). The table shows that D³GM achieves competitive performance with a smaller number of FLOPs, suggesting improved efficiency.

This table compares various SDE diffusion-based approaches, including SGMs, transitionary SGMs and the proposed D³GM. It contrasts their prior distributions, the underlying SDEs used (linear, mean-reverting, or measure-preserving), and their properties, highlighting the advantages of the D³GM. Specifically, it shows how D³GM achieves greater robustness and stability by utilizing measure-preserving RDS.
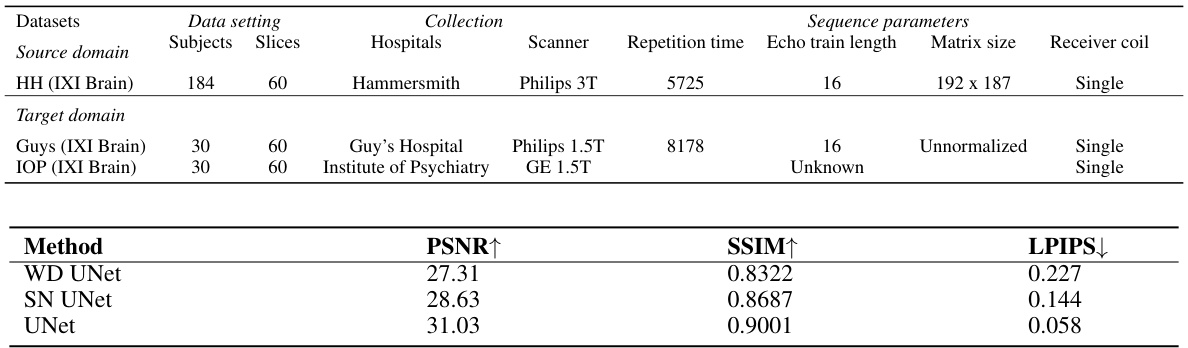
This table provides details on the datasets used in the MRI reconstruction and super-resolution experiments. It lists the source and target domains, including the number of subjects and slices used for training and testing. For the source domain (HH IXI Brain), information on the hospital, scanner type, repetition time, echo train length, matrix size and receiver coil type are also provided. The target domains (Guys IXI Brain and IOP IXI Brain) include similar information, with some data missing for IOP (e.g., sequence parameters). This information is crucial for understanding and reproducing the experimental results.

This table presents a quantitative comparison of different deraining methods on the Rain100H and Rain100L datasets. The metrics used are PSNR (Peak Signal-to-Noise Ratio), SSIM (Structural Similarity Index), and LPIPS (Learned Perceptual Image Patch Similarity). Higher PSNR and SSIM values, and lower LPIPS values indicate better deraining performance. The best performing method for each metric is shown in bold, while the second-best is underlined.
Full paper#