Average gradient outer product as a mechanism for deep neural collapse

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it reveals a data-dependent mechanism for Deep Neural Collapse (DNC), a phenomenon observed in deep learning where data representations become surprisingly rigid. This challenges existing data-agnostic explanations and opens new avenues for understanding and controlling DNC, potentially leading to improvements in model performance and generalization. The findings are particularly relevant to researchers working on feature learning and the theoretical analysis of deep networks.

Visual Insights

#

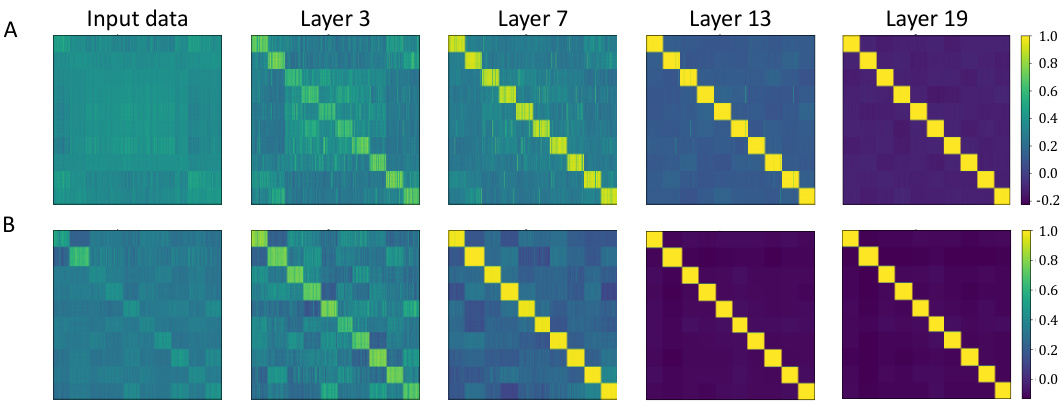
This figure visualizes neural collapse in Deep RFM on CIFAR-10 and MNIST datasets. It shows Gram matrices (inner product matrices) of feature vectors extracted from different layers (1, 3, 7, 13, 19) of the Deep RFM model. The feature vectors are transformed using the Average Gradient Outer Product (AGOP). The data is ordered such that points from the same class are grouped together. The figure demonstrates the progressive collapse of within-class variability, a key characteristic of neural collapse, showcasing the different effects of using cosine and ReLU activation functions.

In-depth insights

#

AGOP’s Role in DNC

#

The paper investigates the Average Gradient Outer Product (AGOP) and its role in Deep Neural Collapse (DNC). AGOP, defined as the uncentered covariance matrix of input-output gradients, is shown to be a data-dependent mechanism driving DNC. The authors introduce Deep Recursive Feature Machines (Deep RFM), a model iteratively applying AGOP projections, demonstrating empirical DNC occurrences. Theoretically, they link AGOP’s role in DNC to kernel learning, explaining DNC as an asymptotic property of Deep RFM under certain conditions. Furthermore, they demonstrate AGOP’s strong correlation with the singular vectors of weight matrices in standard DNNs, suggesting AGOP projections are responsible for within-class variability collapse, a key aspect of DNC in general DNNs. The work bridges data-agnostic explanations of DNC with a data-driven approach, highlighting AGOP as a crucial element in the feature learning process leading to this phenomenon.

Deep RFM Analysis

#

A hypothetical ‘Deep RFM Analysis’ section would delve into the theoretical and empirical underpinnings of the Deep Recursive Feature Machine (Deep RFM) model. It would likely start with a thorough examination of Deep RFM’s architecture, highlighting its iterative feature learning process driven by the Average Gradient Outer Product (AGOP). The analysis would emphasize the role of the AGOP in shaping the learned features, potentially exploring its connection to the model’s ability to learn relevant features effectively. A critical aspect would be an investigation into the model’s capacity to achieve Deep Neural Collapse (DNC), a phenomenon where features from different classes converge. The analysis would likely present both empirical evidence showing DNC in Deep RFM across various datasets and theoretical insights into the mechanism driving this behavior, possibly utilizing asymptotic analyses or kernel methods to explain the convergence. The results would demonstrate how the AGOP-based iterative feature learning leads to the observed DNC, providing a data-dependent explanation for DNC in contrast to data-agnostic models. Finally, it would discuss limitations of the theoretical analysis and the model’s generalizability, opening up avenues for future research.

Singular Vector Collapse

#

Singular vector collapse, a phenomenon observed in deep neural networks, describes the convergence of weight matrix singular vectors towards a low-dimensional subspace during training. This collapse is strongly linked to the emergence of neural collapse, a specific geometric structure in the final layers. While the exact mechanisms driving this collapse are still under investigation, evidence suggests a close relationship with the average gradient outer product (AGOP) and the implicit bias of the optimization algorithm. The collapse is not random; it reveals a structured pattern in the learned representations. Understanding singular vector collapse is crucial to explaining neural collapse and the generalization properties of deep networks. Further research is needed to fully elucidate the relationship between AGOP, singular vector dynamics, and the resulting representational properties. This includes exploring the impact of different network architectures, training algorithms, and datasets on the extent and nature of the collapse.

Theoretical Underpinnings

#

The theoretical underpinnings section of a research paper would ideally delve into the mathematical and conceptual frameworks supporting the empirical findings. This would involve a rigorous justification of the core methods, demonstrating their validity and limitations. It’s crucial to explicitly state any assumptions made and discuss their potential impact on the results’ generalizability. A robust theoretical framework might leverage existing mathematical theorems, or, if novel methods are used, the section should provide a formal proof of their correctness. Furthermore, connections between the theoretical models and the real-world phenomena being studied should be clearly established, explaining how the theoretical constructs translate to the observed behavior. Addressing potential limitations of the theoretical approach, such as the use of simplifying assumptions or the applicability to specific contexts, is also vital for ensuring the work’s credibility and scope. A strong theoretical foundation significantly enhances the paper’s impact by providing a deep understanding of the underlying mechanisms and guiding further research.

Future Research

#

Future research directions stemming from this work could explore extending the theoretical analysis to more complex network architectures and training regimes. Investigating the interplay between the AGOP, the Neural Feature Ansatz, and other factors influencing deep neural collapse is crucial. Furthermore, empirical studies on a wider variety of datasets and tasks would strengthen the findings. A particularly promising avenue is to examine the implications of the AGOP for transfer learning and domain adaptation, given its role in feature representation. Finally, developing practical algorithms that leverage the AGOP to improve generalization and robustness would be highly valuable.

More visual insights

#

More on figures

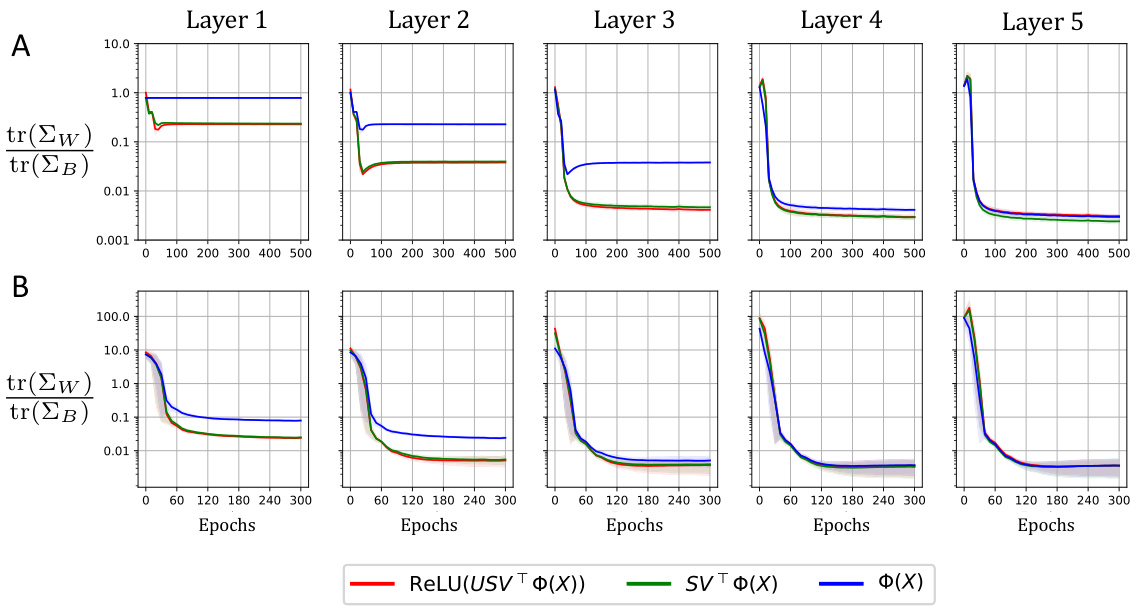
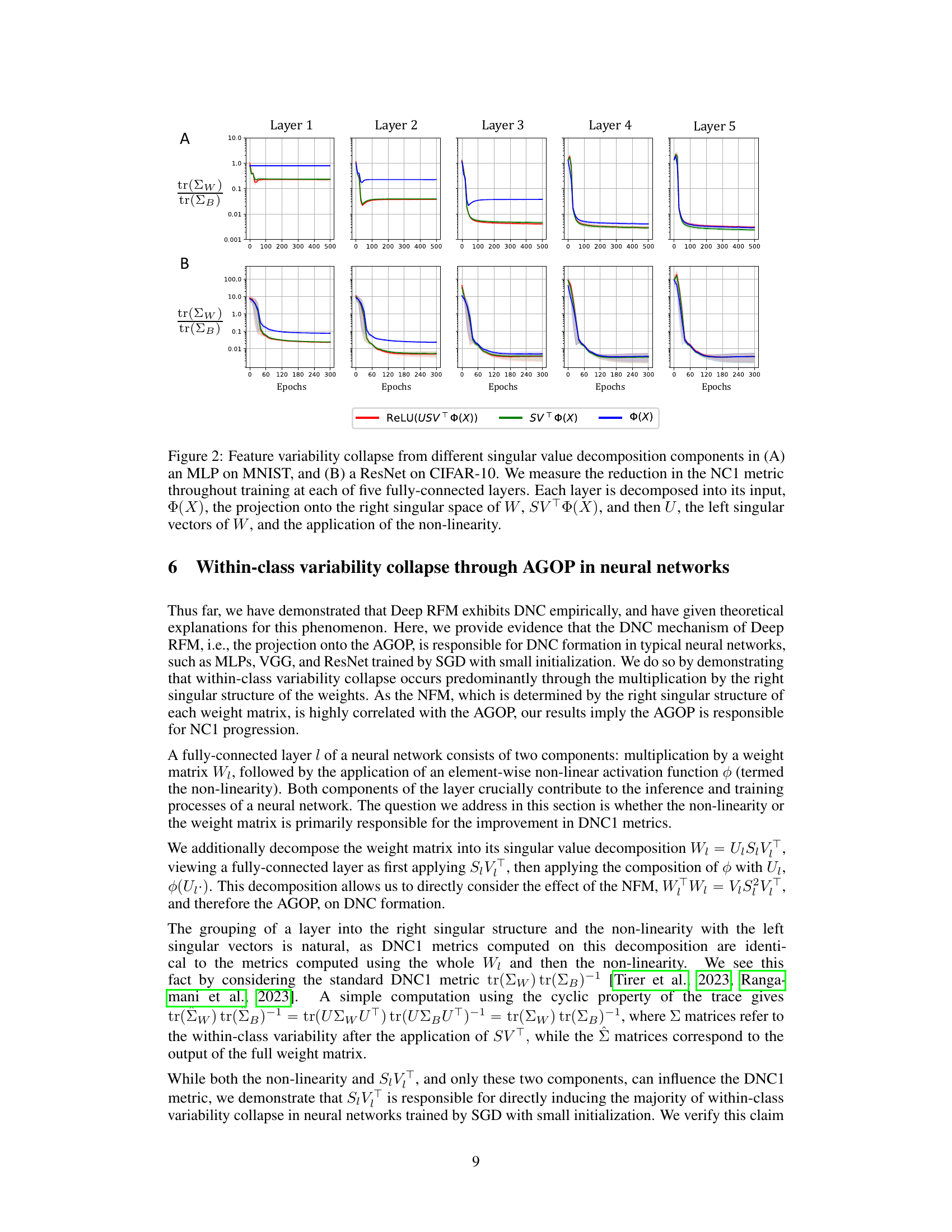
This figure visualizes how different components of a neural network layer contribute to the reduction of within-class variability (NC1 metric). It shows the NC1 metric’s evolution during training for MLP and ResNet models on MNIST and CIFAR-10 datasets, respectively. The layer is decomposed into three parts: the original input, the projection onto the right singular vectors of the weight matrix, and finally the application of non-linearity after projection onto the left singular vectors. The results highlight the dominant role of the right singular vectors in reducing within-class variability.

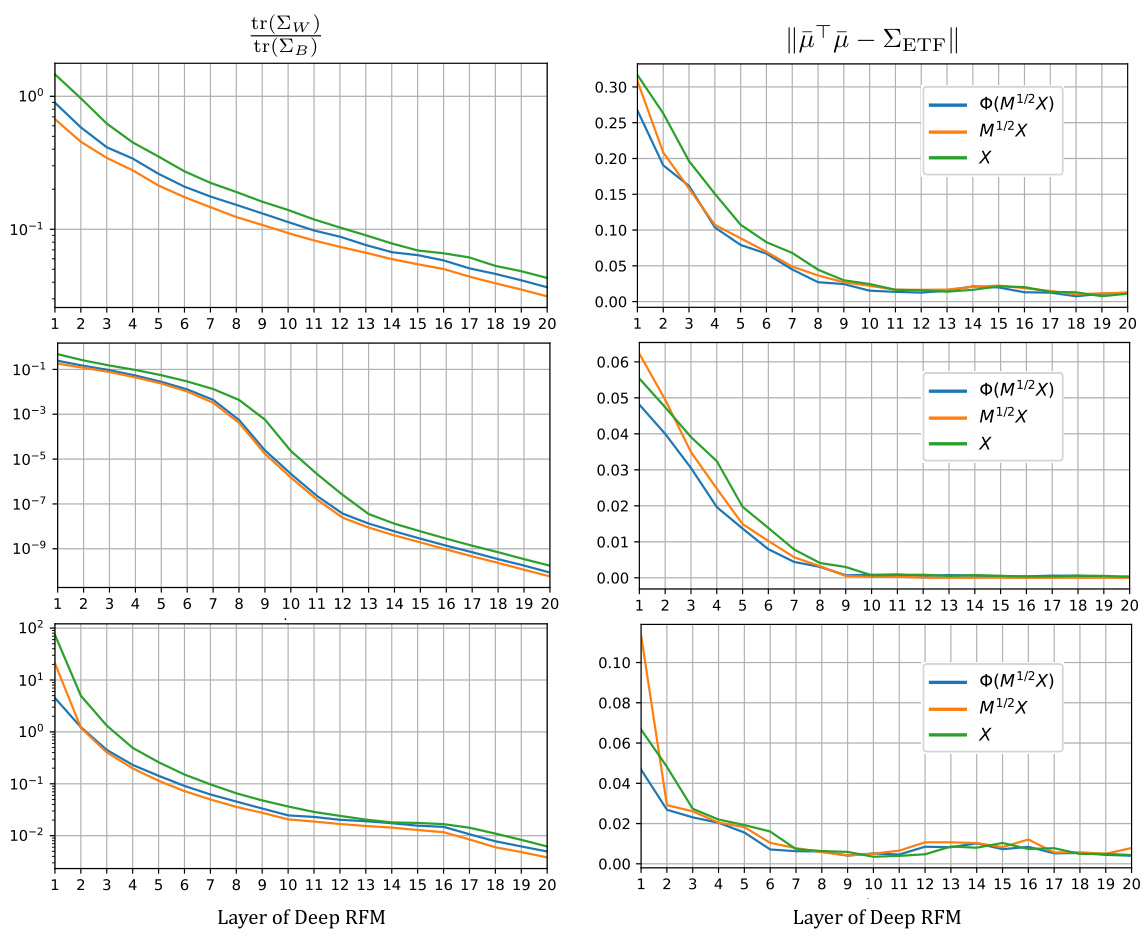
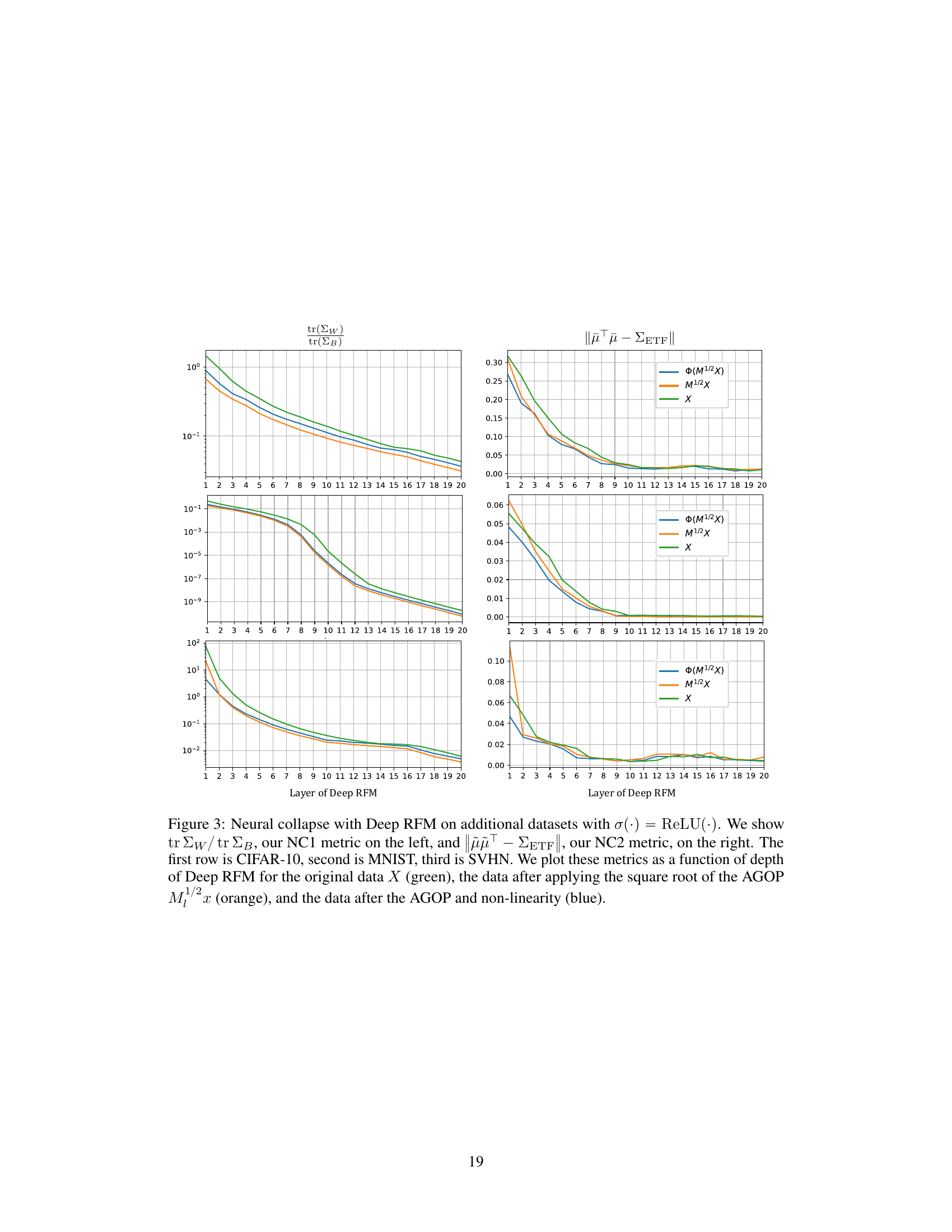
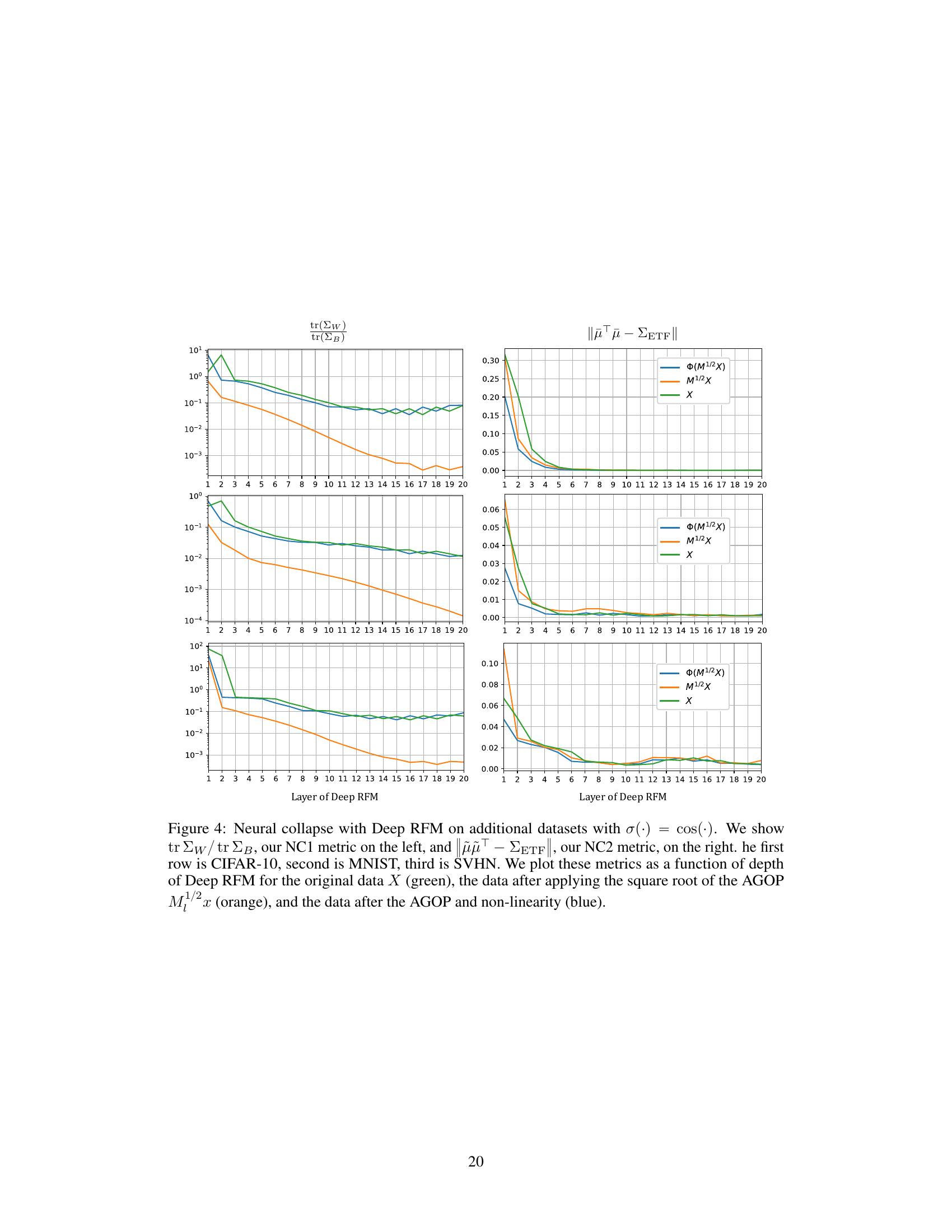
This figure shows the results of applying Deep RFM with ReLU activation function on three different datasets: CIFAR-10, MNIST, and SVHN. It plots two key metrics of neural collapse (NC1 and NC2) across multiple layers of the Deep RFM model. The plots compare the metrics for the original data, the data after transformation by the AGOP’s square root, and the data after both AGOP transformation and the ReLU nonlinearity. The aim is to show that the AGOP is responsible for the collapse in Deep RFM.

This figure visualizes the neural collapse phenomenon in Deep RFM across three datasets (CIFAR-10, MNIST, and SVHN) using the ReLU activation function. It demonstrates the effect of applying the average gradient outer product (AGOP) on the within-class variability and orthogonality properties of the data representations at different layers of the Deep RFM network. The plots show that projection onto the AGOP significantly improves the neural collapse metrics, indicating the AGOP’s crucial role in the process.

This figure visualizes neural collapse in Deep RFM on CIFAR-10 and MNIST datasets. It shows Gram matrices (inner product matrices) of feature vectors extracted from different layers (1, 3, 7, 13, 19) of the Deep RFM network. The features are transformed using the Average Gradient Outer Product (AGOP) before computing the Gram matrices. The data is ordered such that points from the same class are adjacent. The color intensity represents the inner product value, with yellow indicating a value of 1 (similar features) and dark blue indicating -1 (dissimilar features). The figure demonstrates how the within-class variability collapses as the network deepens, showing the effectiveness of AGOP in inducing neural collapse.

This figure visualizes neural collapse in Deep RFM on CIFAR-10 and MNIST datasets. It shows Gram matrices (inner product matrices) of feature vectors from different layers (1, 3, 7, 13, 19) of the Deep RFM. The feature vectors are transformed using the Average Gradient Outer Product (AGOP). The data is ordered such that points from the same class are together. Different non-linearities (cosine and ReLU) are used for CIFAR-10 and MNIST, respectively. The figure demonstrates how the within-class variability decreases as the network depth increases, indicating neural collapse.

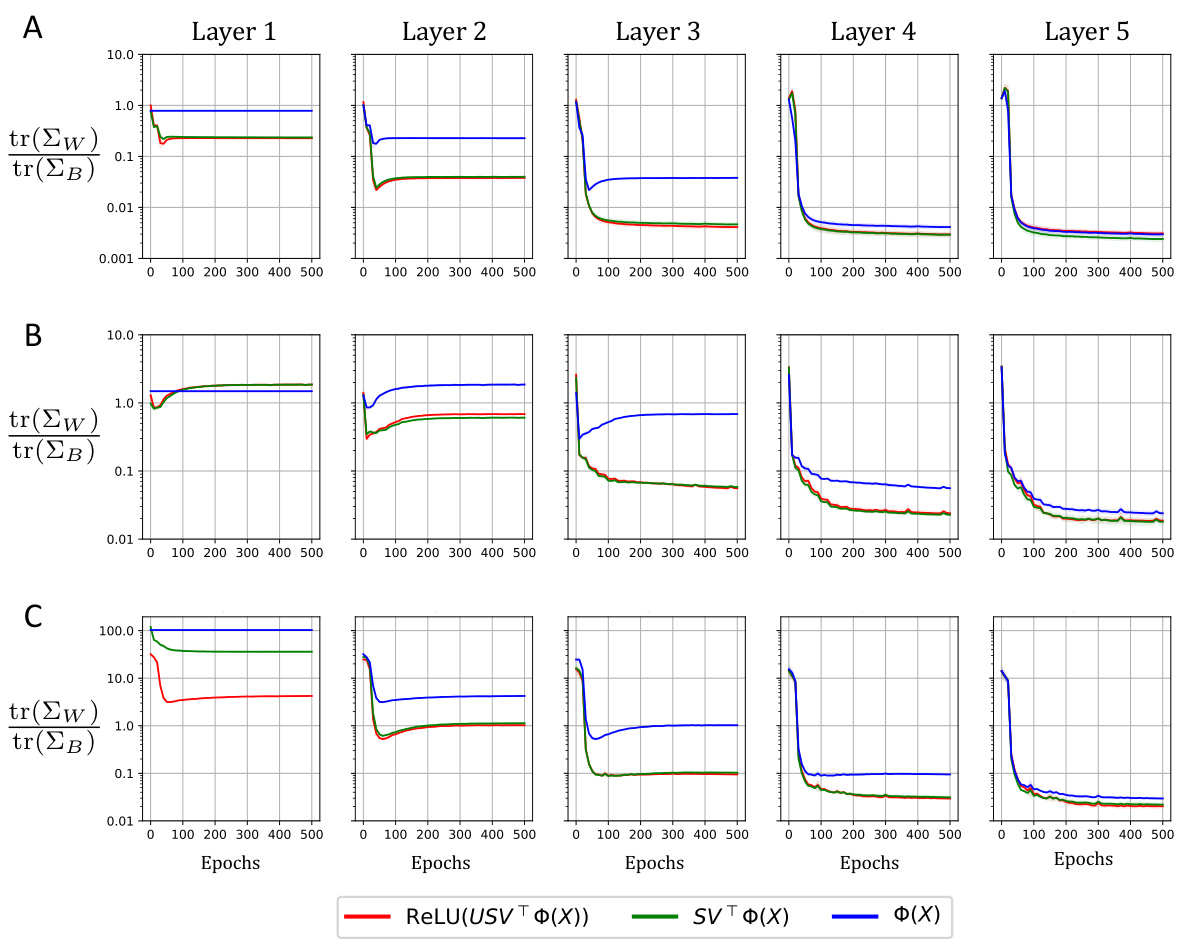
This figure visualizes how different singular value decomposition components of a neural network layer contribute to the reduction of within-class variability (NC1 metric) during training. It shows the NC1 metric’s evolution across five fully-connected layers in both an MLP (MNIST dataset) and a ResNet (CIFAR-10 dataset). The decomposition highlights the input (Φ(X)), the projection onto the right singular space (SVTΦ(X)), and finally the application of the non-linearity to the left singular vectors (ReLU(USVTΦ(X))). This helps understand which components are most responsible for the decrease in within-class variability.

This figure visualizes the feature variability collapse (NC1) from different singular value decomposition components in an MLP and a ResNet. The reduction in NC1 metric is measured throughout the training process for five fully-connected layers. Each layer is broken down into its input, projection onto the right singular space of the weight matrix, projection onto the left singular vectors of the weight matrix, and finally the application of the non-linearity. This decomposition helps to understand the role of each component in the collapse.

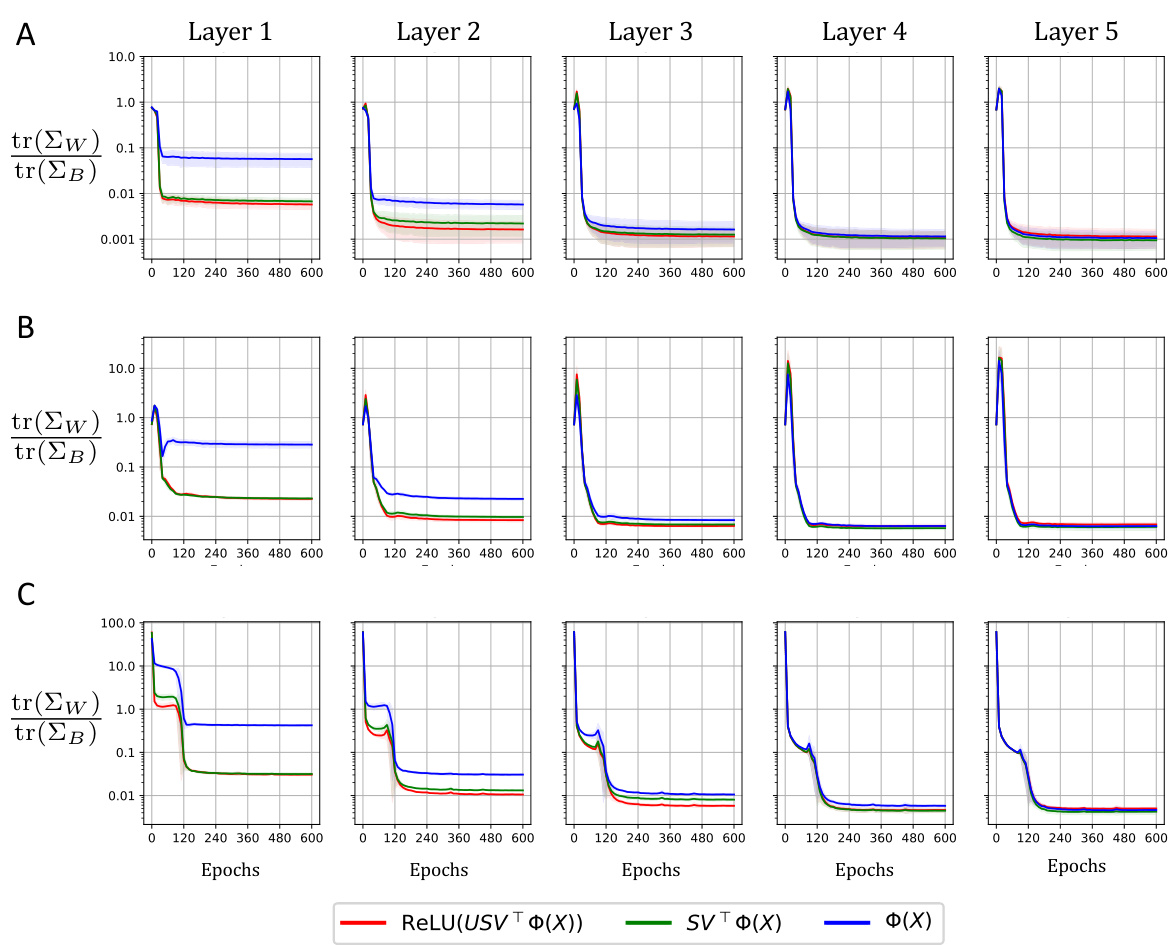
This figure visualizes how feature variability collapse (NC1 metric) changes throughout the training process for different singular value decomposition components. It shows the NC1 metric for Multilayer Perceptron (MLP) on MNIST dataset and Residual Network (ResNet) on CIFAR-10 dataset across five fully-connected layers, comparing the input (X), projection onto right singular space (SV^T(X)), and the result after applying left singular vectors and non-linearity (ReLU(USV^TΦ(X))).

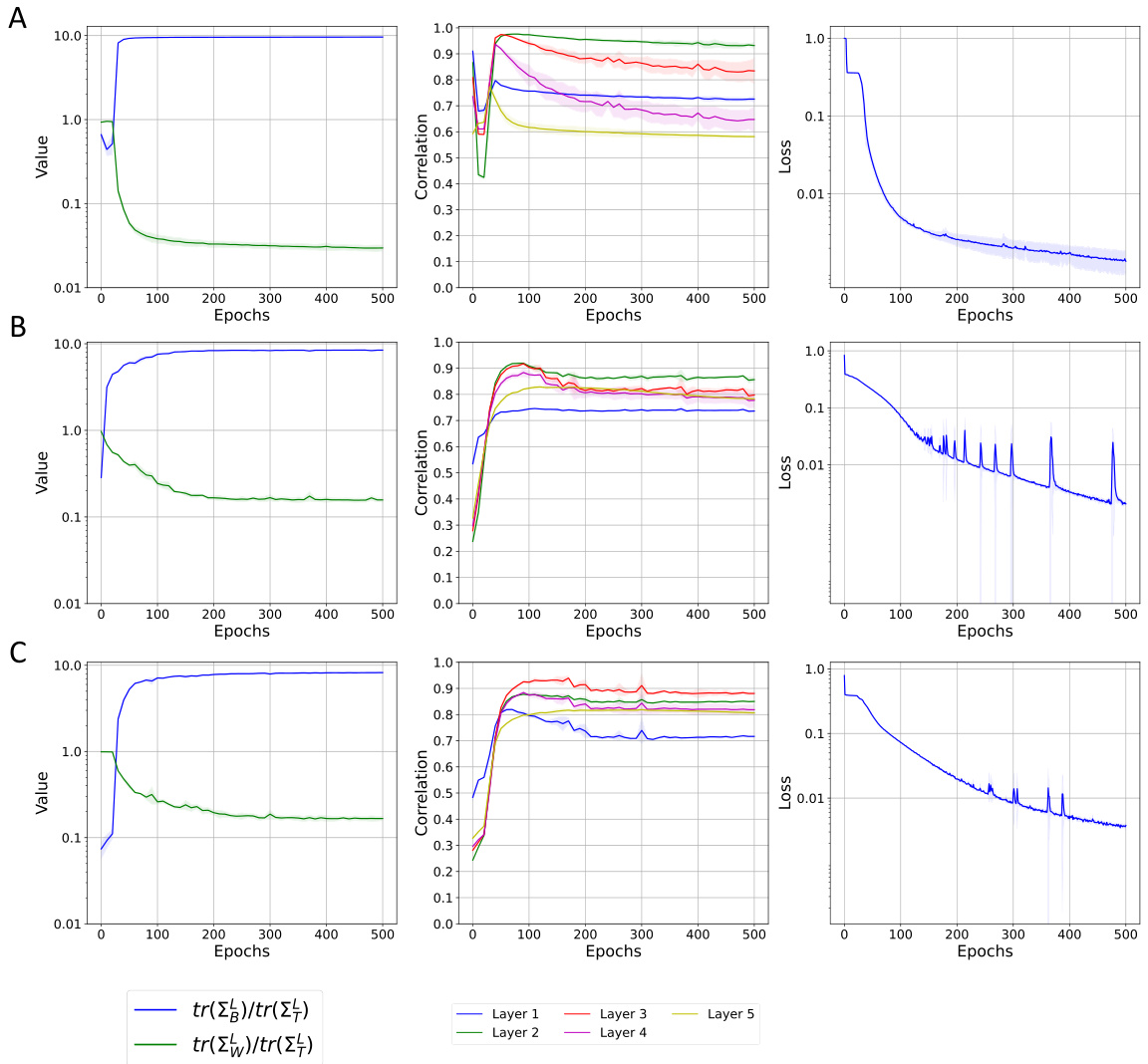
This figure analyzes feature variability collapse during training of neural networks, specifically MLPs and ResNets. It examines the impact of different components of a fully connected layer (input, right singular space projection, and application of non-linearity) on the NC1 metric (within-class variability) across multiple layers. The results highlight the role of the right singular structure in driving the collapse.

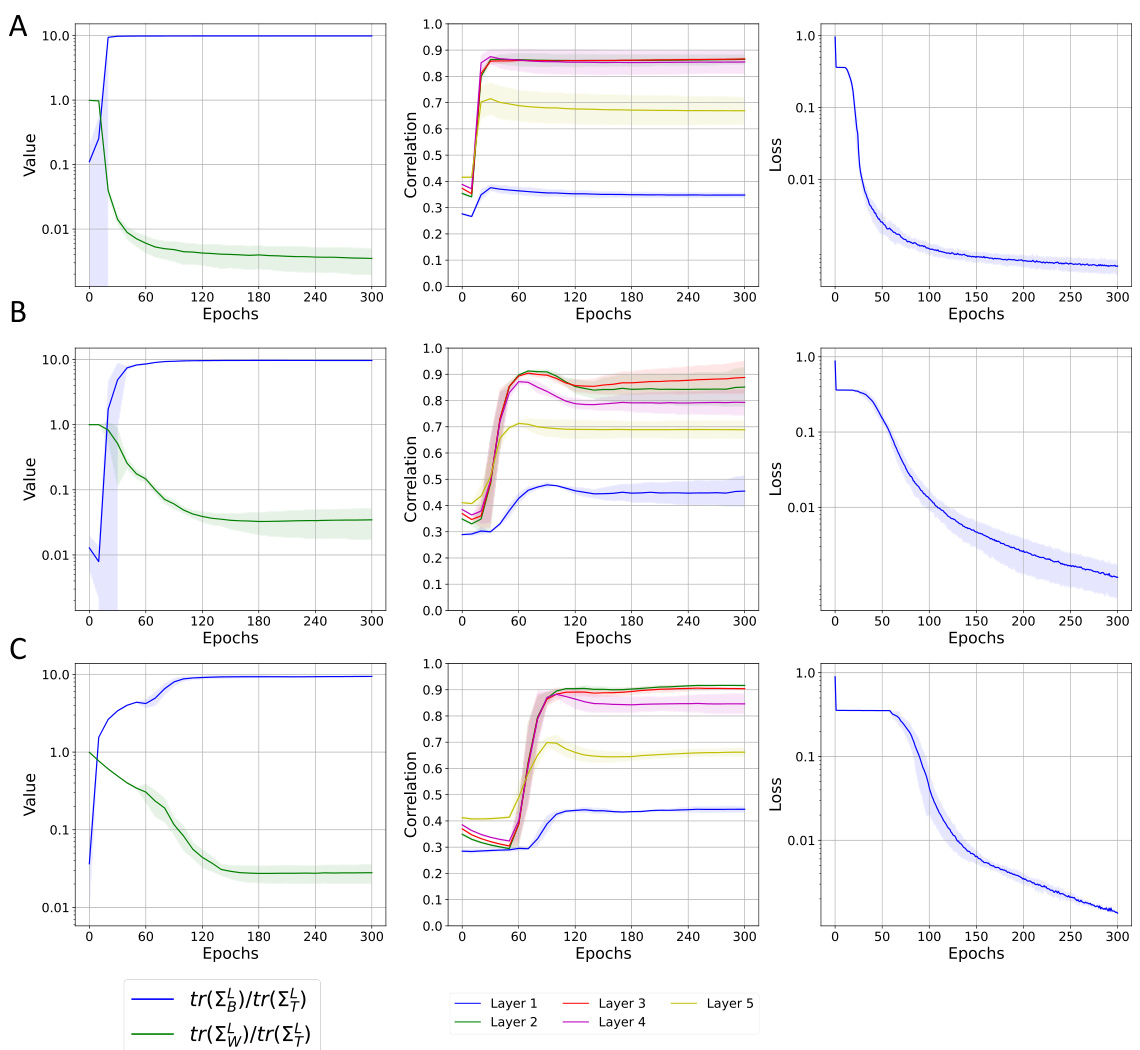
This figure shows how within-class variability changes during the training of an MLP and a ResNet. The reduction in the NC1 metric (a measure of within-class variability) is tracked across five fully connected layers. The figure breaks down each layer’s contribution into three components: the original input (X), the projection onto the right singular vectors of the weight matrix (SVT(X)), and finally the effect of the left singular vectors and the non-linearity (ReLU(USVT(X))). This analysis helps determine the primary influence on reducing within-class variability, allowing to highlight the role of the weight matrix in neural collapse.

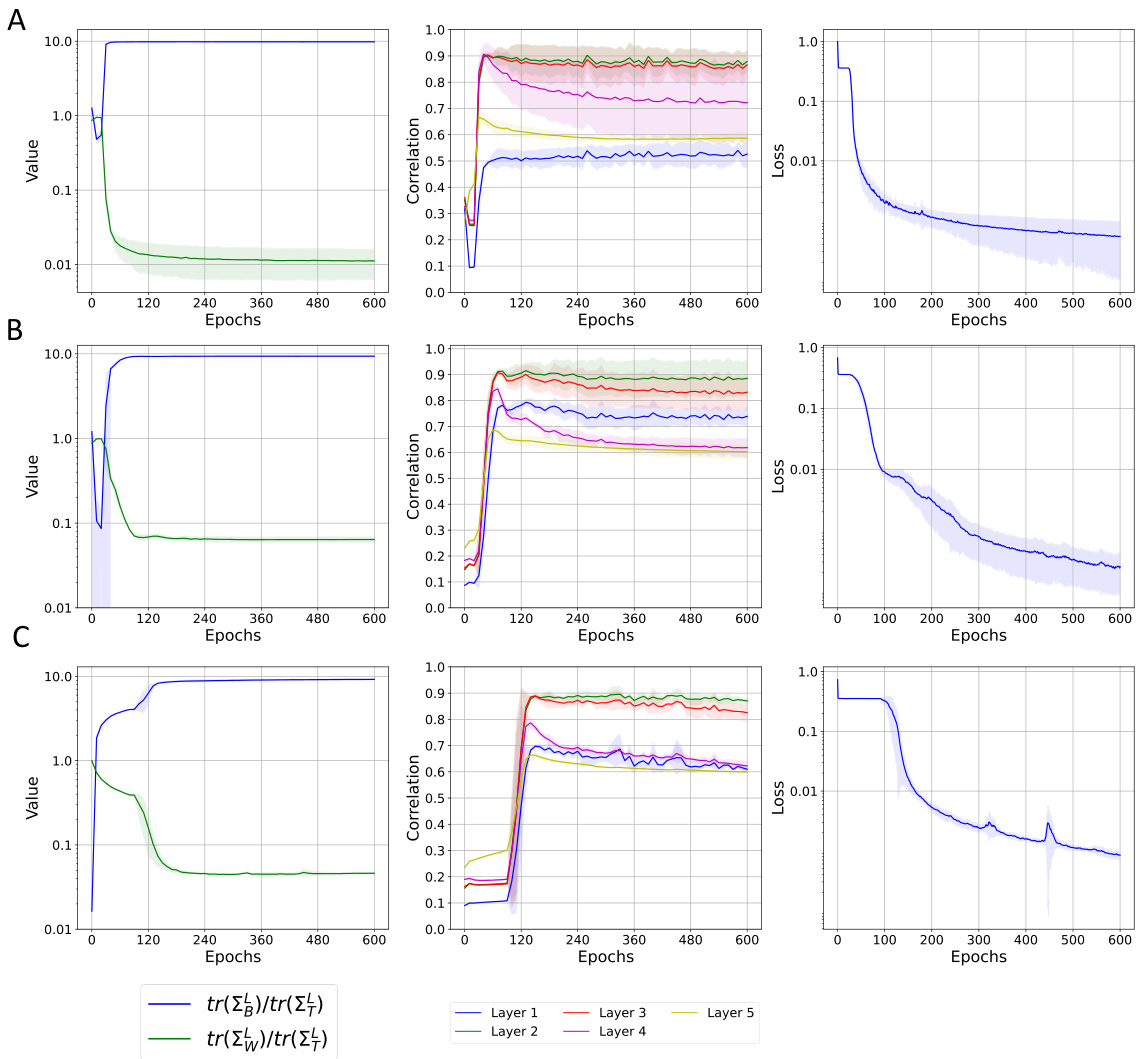
This figure shows how feature variability collapse (a key aspect of Neural Collapse) changes across different layers of neural networks (MLP and ResNet) during training. It breaks down each layer’s contribution into three components: the original input features (X), the projection onto the right singular vectors of the weight matrix (SV^T(X)), and the final output after applying the left singular vectors and non-linearity (ReLU(USV^T(X))). By comparing the within-class variability (NC1 metric) of these components, the figure illustrates the role of the singular value decomposition in driving the collapse.

Full paper

#