↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Transformers’ success hinges on self-attention mechanisms, but their design relies heavily on heuristics. This paper addresses this by showing a fundamental connection between self-attention and Kernel Principal Component Analysis (KPCA). It demonstrates that self-attention projects query vectors onto the principal component axes of its key matrix. This novel understanding reveals inherent limitations of traditional self-attention regarding noisy data.
The research then introduces Attention with Robust Principal Components (RPC-Attention), a novel attention mechanism designed to be robust against data contamination. Experiments on object classification, language modeling, and image segmentation tasks demonstrate that RPC-Attention outperforms traditional softmax attention, especially when dealing with noisy or corrupted datasets. This provides a more principled approach to attention mechanism design, potentially leading to significant improvements in various deep learning applications.
Key Takeaways#
Why does it matter?#
This paper is crucial because it offers a novel theoretical framework for understanding self-attention, a core mechanism in transformers. By connecting self-attention to kernel PCA, it provides a principled basis for designing and improving attention mechanisms, paving the way for more robust and efficient models. The introduction of RPC-Attention, a robust alternative to standard self-attention, is particularly important for dealing with noisy or corrupted data, a common challenge in many applications. This work opens avenues for developing new types of attention mechanisms and advancing the field of deep learning.
Visual Insights#
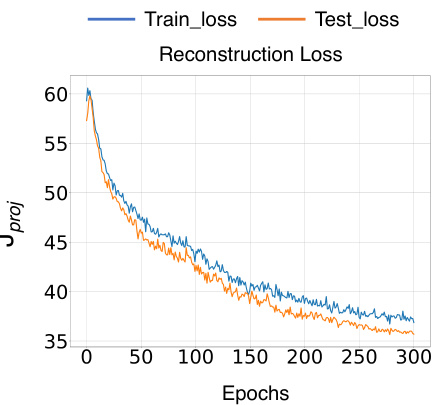
This figure shows the training and testing reconstruction loss of a Vision Transformer (ViT-tiny) model trained on the ImageNet-1K dataset. The reconstruction loss is calculated as the mean squared distance between the original data points and their projections onto the principal component axes. The plot shows that the reconstruction loss decreases over time, indicating that the model learns to perform kernel PCA by implicitly minimizing the projection loss. This supports the paper’s claim that self-attention layers in transformers learn to perform kernel PCA.
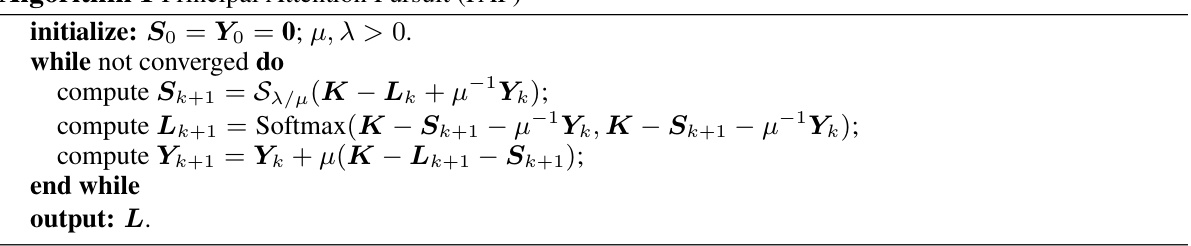
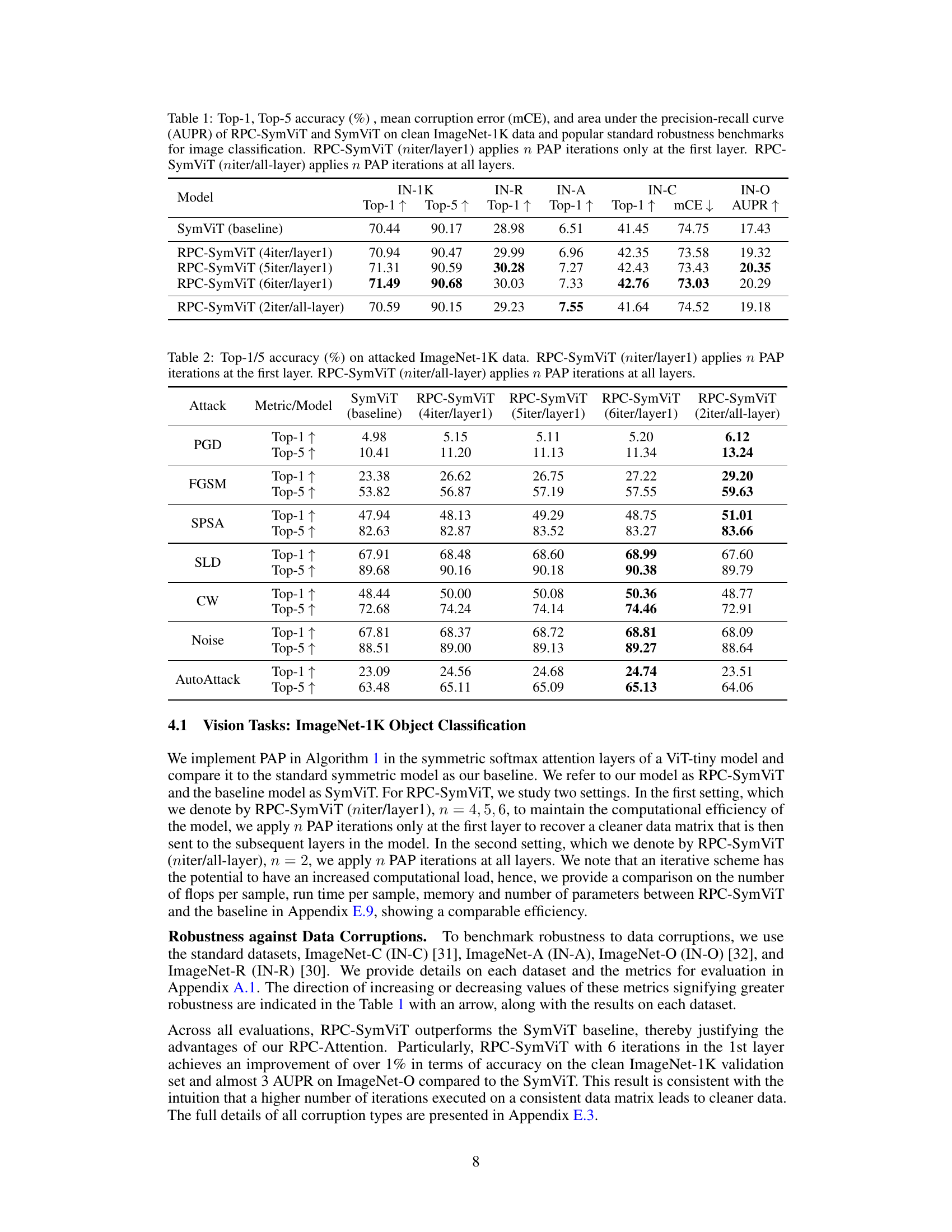
This table presents the performance comparison between RPC-SymViT and SymViT models on ImageNet-1K dataset and its corrupted versions for image classification. It shows the top-1 and top-5 accuracy, mean corruption error, and AUPR. The RPC-SymViT model applies the Principal Attention Pursuit (PAP) algorithm with varying numbers of iterations (niter) either only to the first layer or all layers of the model.
In-depth insights#
Self-Attention’s Roots#
The heading ‘Self-Attention’s Roots’ prompts a deep dive into the foundational understanding of self-attention mechanisms. A thoughtful analysis would explore its origins, tracing its development from simpler attention models and highlighting key conceptual advancements. It would likely discuss the mathematical underpinnings, such as the dot-product attention formulation and its connection to kernel methods. The role of linear transformations in projecting input data into query, key, and value spaces is crucial. A discussion of the impact of the softmax function in normalizing attention weights is also essential. Furthermore, a compelling analysis would contrast self-attention with other attention mechanisms, exploring its unique strengths and limitations, such as its quadratic complexity compared to alternatives. Finally, a comprehensive examination should touch upon the broader theoretical frameworks that underpin self-attention, drawing connections to established concepts in linear algebra, information theory, and machine learning in general.
Robust PCA Attention#
The concept of “Robust PCA Attention” merges the robustness of Principal Component Analysis (PCA) with the mechanism of self-attention in deep learning models. Standard PCA is sensitive to outliers, impacting its effectiveness in real-world applications with noisy data. Robust PCA algorithms mitigate this sensitivity by identifying and removing outliers before performing PCA, leading to more reliable principal components. By integrating robust PCA into self-attention, the resulting “Robust PCA Attention” aims to improve the attention mechanism’s accuracy and stability in the presence of noise or corrupted data. This approach could be particularly beneficial in tasks where data quality is variable or subject to contamination, such as image recognition with noisy images or natural language processing with ambiguous text. A key challenge lies in efficiently implementing robust PCA within the self-attention framework, ensuring computational feasibility for large-scale models. The resulting attention weights should be less susceptible to noisy data, yielding more robust model behavior and potentially improved generalization. Further investigation into the effectiveness of various robust PCA algorithms and the optimal integration strategy within the self-attention architecture is crucial.
Empirical Validation#
An Empirical Validation section in a research paper would rigorously test the study’s hypotheses using real-world data. It would detail the methodologies employed, including the datasets used, the chosen metrics, and the statistical methods for analysis. Robustness checks are crucial, assessing the model’s performance under various conditions and against different types of noise or adversarial attacks. The results would be presented clearly and comprehensively, often including tables, figures, and error bars to demonstrate statistical significance. A thorough discussion of the findings would compare the observed results to the expected outcomes, explaining any discrepancies or unexpected outcomes. Ultimately, a successful Empirical Validation strengthens the paper’s conclusions by providing strong evidence supporting its claims, highlighting both successes and limitations of the proposed methods.
Future Work: Multi-layer#
Extending the kernel PCA framework to analyze multi-layer transformers presents a significant challenge and exciting opportunity. A crucial aspect would be handling the complex interactions between layers, which is not captured by the single-layer analysis presented. This may involve developing new mathematical tools to characterize the evolution of the feature space and its principal components across layers, potentially drawing upon techniques from dynamical systems theory or deep learning theory. Another key area is robustness analysis across multiple layers, investigating whether the advantages of RPC-Attention remain in a deeper network, and potentially developing layer-specific adaptation of the RPC technique. Finally, empirical validation on a wide range of tasks, especially those that require complex long-range dependencies, would be essential to demonstrate the effectiveness of the proposed framework in a full multi-layer context. The ultimate goal would be to develop a comprehensive theory of multi-layer attention grounded in a principled mathematical framework, potentially leading to more efficient and robust transformer architectures.
Limitations: Iterative#
The iterative nature of the proposed RPC-Attention mechanism, stemming from its reliance on the Principal Component Pursuit (PCP) algorithm, presents a key limitation. Each iteration involves computationally expensive operations, potentially increasing the overall runtime and memory footprint, especially when applied to deep networks with numerous layers. While strategies like applying the iterations only to initial layers mitigate this, the scalability to extremely large models remains a concern. Furthermore, the convergence properties of PCP and the optimal number of iterations are not fully explored, requiring further investigation to determine the trade-off between accuracy gains and computational cost. The algorithm’s performance might also be sensitive to parameter tuning (λ, μ), adding complexity. While empirically shown effective, a theoretical analysis of the method’s convergence and robustness is lacking, making it difficult to guarantee its reliability in diverse scenarios. Finally, the generalizability of the approach across different attention architectures or transformer variants needs to be further studied.
More visual insights#
More on figures

This figure shows empirical results supporting Equation 11 in the paper. It plots the average pairwise absolute differences between elements of the vector γ (which should be constant if the value vectors vj capture the eigenvectors of the Gram matrix Kφ). The small standard deviation and near-zero mean support the hypothesis that vj captures these eigenvectors after training. The comparison with the significantly larger magnitudes of the eigenvalues themselves further emphasizes the findings.
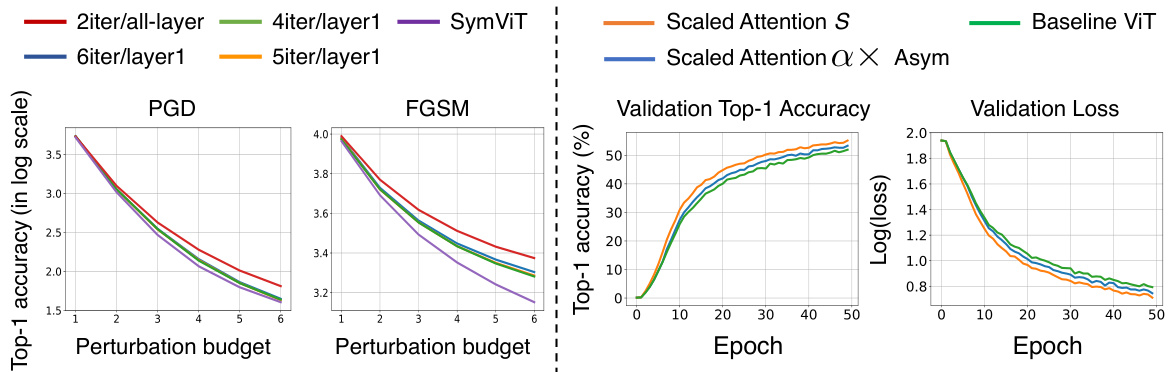
The figure shows two plots. The left plot compares the top-1 accuracy of RPC-SymViT and SymViT models on the ImageNet-1K validation set under PGD and FGSM attacks with varying perturbation budgets. It demonstrates the improved robustness of RPC-SymViT against adversarial attacks. The right plot compares the validation top-1 accuracy and loss curves of Scaled Attention and baseline asymmetric softmax attention models during the first 50 training epochs on the ImageNet-1K dataset. It illustrates the superior performance of Scaled Attention in terms of accuracy and convergence speed.

The left plot shows the robustness of RPC-SymViT against PGD and FGSM attacks compared to the baseline SymViT on the ImageNet-1K dataset. The right plot illustrates the performance of Scaled Attention and baseline asymmetric softmax attention on the validation dataset during the training of ViT-tiny model for the first 50 epochs.

This figure shows the empirical results to verify equation (11) in the paper. The mean and standard deviation of the absolute differences between each pair of elements in the constant vector λa (where a is the eigenvector of the Gram matrix) are plotted for each principal component axis. The plot shows that the differences are close to 0, with small standard deviations across all layers and heads. This indicates that after training, the value matrix V captures the eigenvectors of the Gram matrix, supporting the theory that self-attention performs kernel PCA.
More on tables
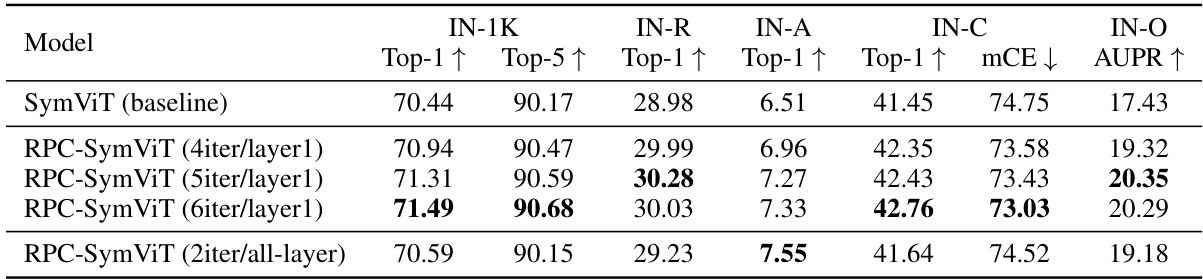
This table presents the performance comparison between RPC-SymViT and SymViT models on ImageNet-1K dataset and its corruptions (ImageNet-C, ImageNet-A, ImageNet-O, ImageNet-R). It shows Top-1 and Top-5 accuracy, mean corruption error (mCE), and area under the precision-recall curve (AUPR). Different versions of RPC-SymViT are evaluated, varying the number of PAP iterations applied to either only the first layer or all layers. SymViT serves as the baseline model.
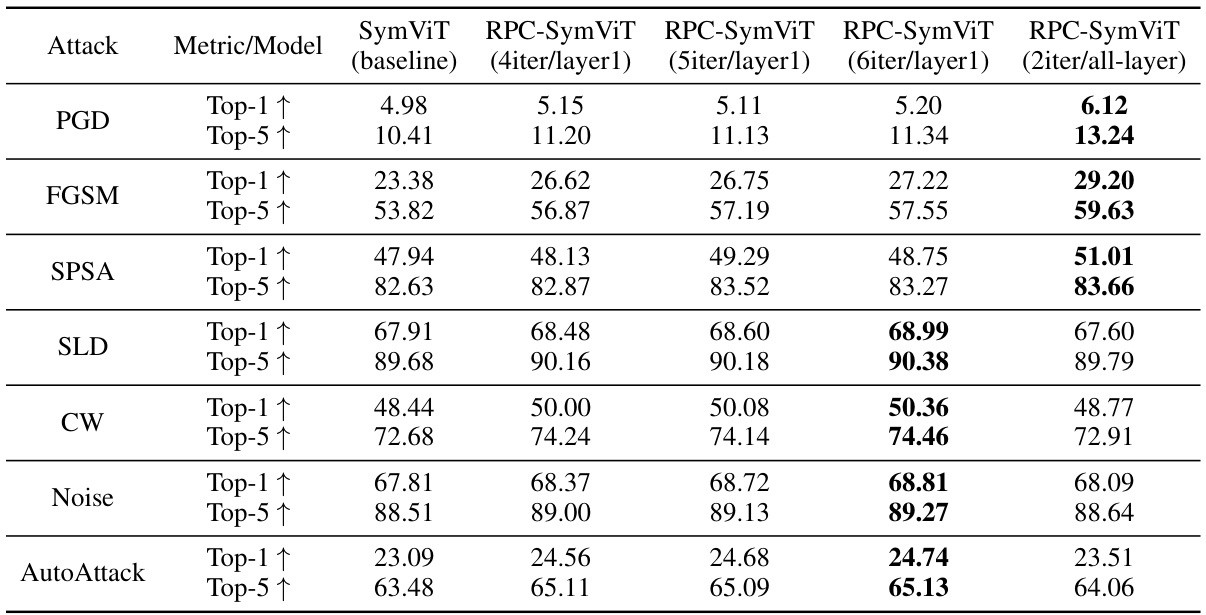
This table presents the top-1 and top-5 accuracy results of different models on the ImageNet-1K dataset after being attacked by various methods. It compares the baseline SymViT model against several variations of the RPC-SymViT model, which incorporates the proposed robust principal component analysis (RPC) based attention mechanism. The variations differ in the number of PAP (Principal Attention Pursuit) iterations applied (either to only the first layer or all layers) and the number of iterations. The attacks used include PGD, FGSM, SPSA, SLD, CW, noise, and AutoAttack, representing diverse attack strategies.

This table presents a comparison of the performance of RPC-SymViT and SymViT models on the ImageNet-1K dataset and several standard robustness benchmarks. The metrics used are Top-1 and Top-5 accuracy, mean corruption error (mCE), and area under the precision-recall curve (AUPR). Different configurations of RPC-SymViT are tested, varying the number of PAP iterations applied either to only the first layer or all layers. The baseline model is SymViT.

This table presents a comparison of the performance of RPC-SymViT and SymViT models on ImageNet-1K dataset and its variations (ImageNet-C, ImageNet-R, ImageNet-A, and ImageNet-O) used for evaluating robustness of models against corruptions and distribution shifts. It shows top-1 and top-5 accuracy, mean corruption error (mCE), and area under the precision-recall curve (AUPR). Different versions of RPC-SymViT are tested, applying the proposed robust principal component analysis (RPC)-based attention mechanism to either only the first layer or all layers of the model. The baseline model is SymViT, a standard Vision Transformer model without RPC-Attention.
This table presents a comparison of the performance of RPC-SymViT and SymViT models on the ImageNet-1K dataset and several standard robustness benchmarks for image classification. The models are evaluated on their top-1 and top-5 accuracy, mean corruption error (mCE), and area under the precision-recall curve (AUPR). The table also shows the effect of applying different numbers of PAP iterations to either only the first layer or all layers of the RPC-SymViT model.

This table presents the results of square attack on ImageNet-1K validation set. The top-1 and top-5 accuracy are reported for both baseline SymViT and RPC-SymViT model with 6 PAP iterations applied only to the first layer. The table shows that RPC-SymViT outperforms the baseline SymViT demonstrating its improved robustness against this adversarial attack.

This table presents the performance of the RPC-SymViT model and the baseline SymViT model on the ADE20K image segmentation task. It shows the mean accuracy and mean Intersection over Union (IOU) for both clean and corrupted data. Different configurations of RPC-SymViT (varying the number of PAP iterations and the layers they are applied to) are compared.

This table presents the performance of RPC-SymViT and SymViT models on ImageNet-1K dataset and its corrupted versions (ImageNet-C, ImageNet-A, ImageNet-O, ImageNet-R). The metrics used are Top-1 accuracy, Top-5 accuracy, mean corruption error (mCE), and area under the precision-recall curve (AUPR). Different configurations of RPC-SymViT are tested, varying the number of PAP iterations applied (either only to the first layer or all layers). The results show the impact of applying the robust principal component analysis (RPC) method on the robustness of the models against various corruptions and perturbations.

This table presents the top-1 and top-5 accuracy of two models, RPC-SymViT-base and SymViT-base, when evaluated on the ImageNet-1K dataset under PGD and FGSM attacks. The attacks use the highest perturbation budget. RPC-SymViT-base incorporates the proposed Robust Principal Component Attention (RPC-Attention) method, and SymViT-base serves as a baseline without this method. The results highlight the improved robustness of RPC-SymViT-base against these adversarial attacks.
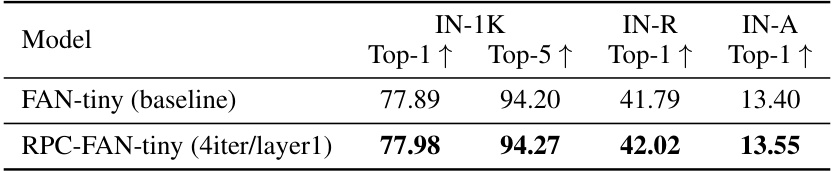
This table presents the performance comparison between RPC-FAN-tiny and FAN-tiny models on ImageNet-1K dataset and its variations (IN-R, IN-A). RPC-FAN-tiny is the proposed model in the paper that uses Robust Principal Component Analysis (RPCA) to improve the robustness of self-attention. The table shows that RPC-FAN-tiny outperforms FAN-tiny in terms of Top-1 and Top-5 accuracy on all datasets. This demonstrates the effectiveness of RPC-Attention in enhancing the model robustness.

This table presents the top-1 and top-5 accuracy of two models, FAN-tiny (baseline) and RPC-FAN-tiny (4iter/layer1), evaluated on the ImageNet-1K dataset under PGD and FGSM attacks. The highest perturbation budget was used for the attacks. The RPC-FAN-tiny model incorporates the Robust Principal Component Attention (RPC-Attention) method, applying the Principal Attention Pursuit (PAP) algorithm 4 times in the first layer. The results show how the RPC-Attention method improves the model’s robustness against adversarial attacks.

This table presents the performance comparison between RPC-SymViT and SymViT models on ImageNet-1K dataset and its corruptions (ImageNet-C, ImageNet-A, ImageNet-O, ImageNet-R). The metrics used are Top-1 accuracy, Top-5 accuracy, mean corruption error, and area under the precision-recall curve. Different configurations of RPC-SymViT are evaluated, varying the number of PAP iterations and whether they are applied to only the first layer or all layers.

This table presents the performance comparison between RPC-SymViT and SymViT models on ImageNet-1K dataset and its corrupted versions (ImageNet-C, ImageNet-A, ImageNet-O, and ImageNet-R). The metrics used are Top-1 and Top-5 accuracy, mean corruption error (mCE), and area under the precision-recall curve (AUPR). RPC-SymViT is a variant of SymViT that incorporates the Robust Principal Component Pursuit (RPC) algorithm. Two variations are presented, applying the RPC algorithm either to only the first layer or to all layers of the model. The results show that RPC-SymViT generally outperforms SymViT, especially on the corrupted datasets, indicating its improved robustness.

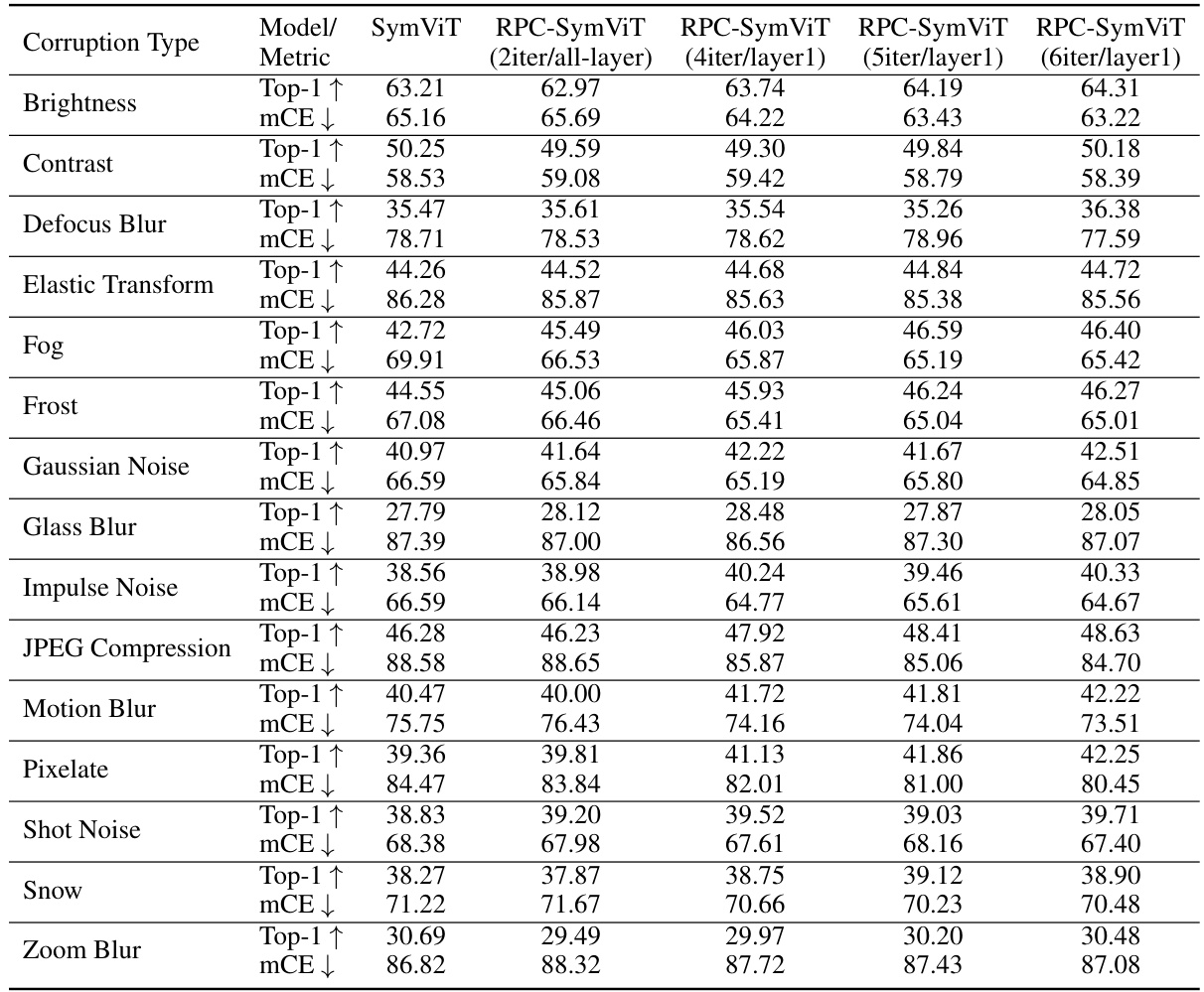
This table presents the performance comparison between RPC-SymViT and SymViT models on ImageNet-1K dataset and its various corrupted versions. It shows the top-1 and top-5 accuracy, mean corruption error (mCE), and area under the precision-recall curve (AUPR) for both models under different settings (number of PAP iterations applied to either only the first layer or all layers). The results are categorized by the type of corruption (brightness, contrast, etc.) and presented to demonstrate the robustness of the RPC-SymViT model compared to the baseline SymViT.

This table presents a comparison of the performance of RPC-SymViT and SymViT models on the ImageNet-1K dataset and several standard robustness benchmarks for image classification. It shows Top-1 and Top-5 accuracy, mean corruption error (mCE), and area under the precision-recall curve (AUPR) for both models under various conditions. The RPC-SymViT model is a variant of the SymViT model that incorporates the proposed robust principal component attention mechanism. The results indicate the performance gain from incorporating this method, particularly on the more challenging robustness benchmarks.
Full paper#