↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Federated learning (FL) faces challenges in communication efficiency and computation costs due to resource-constrained edge devices and the need for privacy-preserving data handling. Existing methods often focus on improving global model aggregation or employing regularization to reduce local model drift, but they might not fully address the computational burden at the client-side. Heterogeneous data distribution across clients further complicates the training process, causing overfitting and model aggregation failures. This paper presents a novel FL paradigm to tackle these issues.
The proposed method utilizes low-precision computation during local model training and communication, while reserving high-precision for model aggregation on the server-side. This significantly reduces both communication and computation costs. The method leverages the stability of moving average for aggregation, theoretically demonstrating its convergence to the optimal solution, even with low-precision local training. Experiments validate the effectiveness of the paradigm, showing comparable performance with 8-bit precision to that of full-precision methods. The reduced model expressiveness from low-precision training also alleviates overfitting, preventing local model drift and ensuring effective aggregation in the heterogeneous data scenario.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in federated learning due to its significant contribution in enhancing efficiency and addressing critical challenges. By proposing and validating a low-precision local training paradigm, it reduces communication and computation costs substantially. This is especially relevant given the resource-constrained nature of edge devices in federated learning scenarios. The theoretical analysis and empirical validation demonstrate the effectiveness of the method, addressing overfitting issues commonly encountered in heterogeneous data settings. Furthermore, its flexibility to integrate with existing algorithms and achieve comparable performance with 8-bit precision opens exciting avenues for future work, such as exploring hardware-specific optimizations for further efficiency improvements.
Visual Insights#
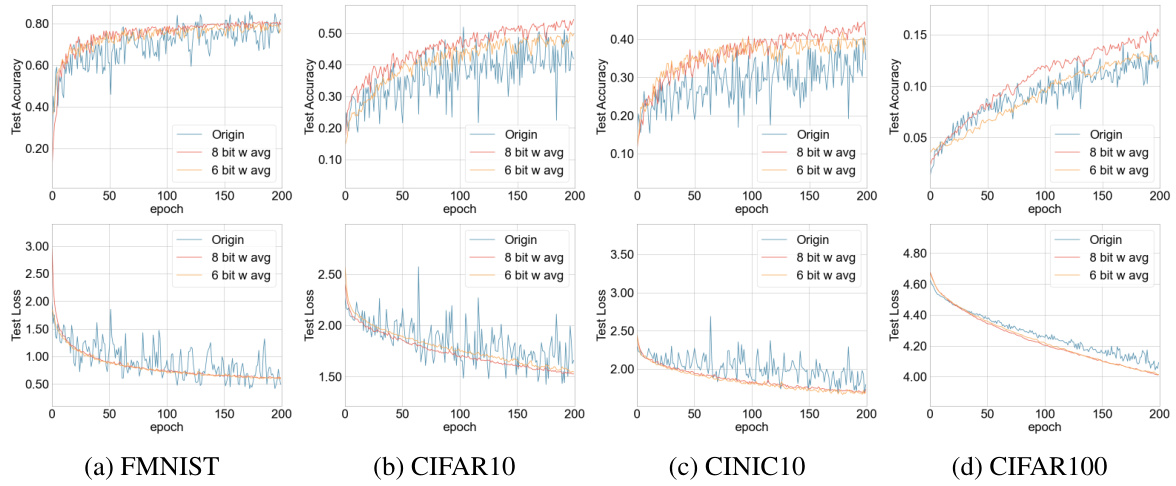
This figure compares the accuracy and loss curves of the FedAvg algorithm using full precision and the proposed low-precision method with 8-bit and 6-bit precision. The results are shown for four datasets: FashionMNIST, CIFAR10, CINIC10, and CIFAR100. The low-precision method demonstrates improved stability and reduced fluctuation compared to the full-precision method, highlighting its effectiveness in mitigating model drift and overfitting issues in federated learning.

This table shows the results of the proposed low-precision federated learning method integrated with FedAvg. The accuracy is tested under different levels of data heterogeneity (α = 0.01, 0.04, 0.16) and quantization precision (32 bits, 8 bits, 6 bits) on four datasets (FMNIST, CIFAR10, CINIC10, CIFAR100). The results are shown with and without the moving average aggregation technique used in the server. The table demonstrates that using 8-bit precision with moving average achieves comparable accuracy to the full precision (32-bit) model.
In-depth insights#
Low-Precision FL#
Low-Precision Federated Learning (FL) is a technique that aims to improve the efficiency of FL by performing computations and communication with lower precision. This approach has several advantages: it reduces communication costs and computational overheads on resource-constrained edge devices, as well as relieving the overfitting problem often seen in local training. The core idea is to train local models with low precision (e.g., 8-bit), then aggregate them on a server using high precision. Surprisingly, high-accuracy global models can be recovered despite the lower precision in local training, demonstrating that low precision is sufficient. This paradigm is flexible, integrating with existing FL algorithms, and offering considerable savings in training memory and communication costs, often while maintaining or exceeding the accuracy of full-precision methods. However, theoretical guarantees need careful consideration and depend on assumptions about data distribution and model characteristics. While this method offers significant advantages, potential limitations include the theoretical constraints which may not always be met in real-world scenarios, and the implementation challenges, including reliance on specialized hardware to fully realize the potential speed-ups.
Theoretical Convergence#
A theoretical convergence analysis in a machine learning context, specifically within the framework of federated learning (FL), rigorously examines the algorithm’s ability to reach an optimal solution. It often involves demonstrating that the model parameters converge to a point that minimizes the loss function, under specific assumptions. Key assumptions frequently include the smoothness and strong convexity of the loss function and bounds on the variance of stochastic gradients. The analysis may address different participation scenarios (full vs. partial) and the impact of non-independent and identically distributed (non-iid) data, conditions commonly found in real-world FL deployments. Convergence rates, often expressed as a function of the number of iterations (e.g., O(1/T)), are crucial in assessing the algorithm’s efficiency. A complete analysis should account for the effects of data heterogeneity and the use of low-precision computation, common considerations in FL to improve efficiency and privacy.
Overfitting Relief#
Overfitting, a common challenge in machine learning, is exacerbated in federated learning (FL) by the non-independent and identically distributed (non-IID) nature of client data. This paper posits that low-precision local training serves as a powerful regularizer, mitigating overfitting. By limiting the model’s expressiveness through reduced precision arithmetic, the local model is prevented from memorizing idiosyncrasies in its limited training data. This effect is particularly beneficial in heterogeneous FL settings where client data varies significantly, as it prevents the models from diverging substantially. The resulting more generalized local models, despite lower precision, then lead to improved global model aggregation and performance, avoiding the pitfalls of overfitting-induced model drift and aggregation failure. This unexpected benefit of low-precision training simplifies FL and enhances its robustness to data heterogeneity. The authors demonstrate this empirically, showing that low-precision methods match or surpass the performance of full-precision approaches. Therefore, low precision is not merely a computational efficiency technique but also a regularization method to improve model generalizability in FL.
Efficient FL Designs#
Efficient Federated Learning (FL) designs are crucial for practical implementation due to the inherent communication and computational constraints. Reducing communication overhead is a primary focus, often achieved through techniques like model compression (pruning, quantization), gradient compression, or sparse updates. Computation efficiency is addressed by methods such as local model training, employing computationally lightweight models, and using efficient optimization algorithms. Balancing communication and computation is key; a highly communication-efficient method that requires excessive local computation may not be optimal. Furthermore, robustness to data heterogeneity across participating clients is paramount, with many designs focusing on techniques like personalized federated learning to cater to the specific characteristics of individual client data distributions. Ultimately, the most efficient FL design will often depend on the specific application and constraints, requiring careful consideration of the trade-offs between communication, computation, and the degree of personalization.
Future Work#
Future research directions stemming from this low-precision federated learning paradigm could explore several promising avenues. Extending the theoretical analysis to encompass more realistic FL settings such as heterogeneous client data distributions, and more complex communication models is crucial. Investigating the impact of different quantization techniques and their interplay with various optimization algorithms can further enhance model accuracy and efficiency. Furthermore, developing robust and adaptive methods for selecting the optimal precision level dynamically based on the data characteristics and network conditions is a key area for future development. Finally, applying this low-precision framework to a wider range of FL applications and exploring its benefits on resource-constrained edge devices holds significant potential. This would necessitate extensive experimental validation across diverse benchmarks and real-world scenarios.
More visual insights#
More on figures
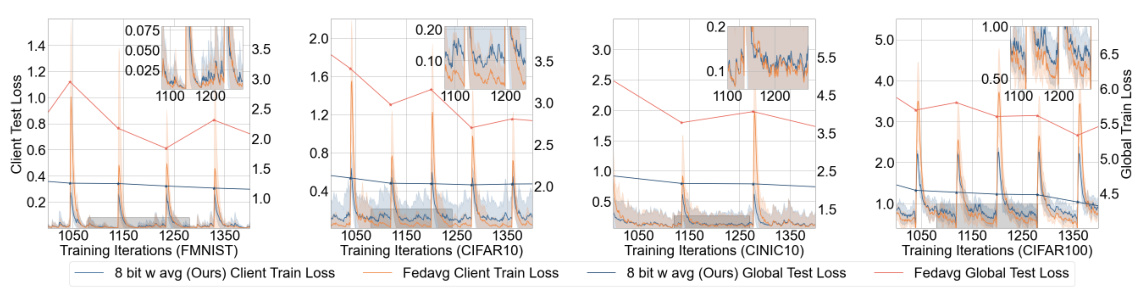
This figure compares the training and testing loss curves for FedAvg (full precision) and the proposed low-precision method. It shows that while the low-precision method has higher local training loss, it significantly reduces the global testing loss and exhibits greater stability, indicating that it effectively mitigates overfitting.

This figure compares the training cost, communication cost, and accuracy of different model compression and low-precision training methods on the CIFAR10 dataset. The methods include HeteroFL, SplitMix, and the proposed low-bit moving average method. The varying percentages shown in parentheses represent the fraction of the global model used in client training. The figure showcases the trade-offs between these factors, illustrating how the proposed method achieves high accuracy while reducing resource consumption.

This figure compares the accuracy and loss curves for FedAvg with full precision and the proposed low-precision method using 8-bit and 6-bit precision. The results show that the low-precision method achieves comparable accuracy while demonstrating improved stability and reduced fluctuation. This is attributed to the low-precision local training preventing client models from diverging and overfitting their local datasets, thereby leading to more stable aggregation.
More on tables

This table presents the results of the proposed low-precision federated learning method integrated with FedAvg on various datasets. It showcases the impact of different levels of heterogeneity (α) and precision (bits) on the model’s performance, comparing models trained with moving averages to those without. Notably, the results highlight the ability of the low-precision method (with moving averages) to achieve comparable performance to the full-precision (32-bit) method even at 8-bit precision, while demonstrating that the low-precision method without moving average suffers performance degradation.

This table presents the results of the proposed low-precision federated learning method integrated with FedAvg, showing its performance across different levels of data heterogeneity and quantization precision. The results are compared against the full-precision version of FedAvg, highlighting the effectiveness of the low-precision approach even when using as few as 8 bits of precision. The impact of removing the moving average component of the method is also demonstrated.

This table presents the results of integrating the proposed low-precision federated learning method with the FedAvg algorithm. It shows the accuracy achieved across various datasets (FashionMNIST, CIFAR10, CINIC10, CIFAR100) under different levels of data heterogeneity (α = 0.01, 0.04, 0.16) and quantization precisions (32 bits, 8 bits, 6 bits). The results are compared with and without the use of moving average in the server-side aggregation. The table demonstrates that low-precision local training with moving average effectively matches the accuracy of full-precision training, significantly reducing communication and computation costs.
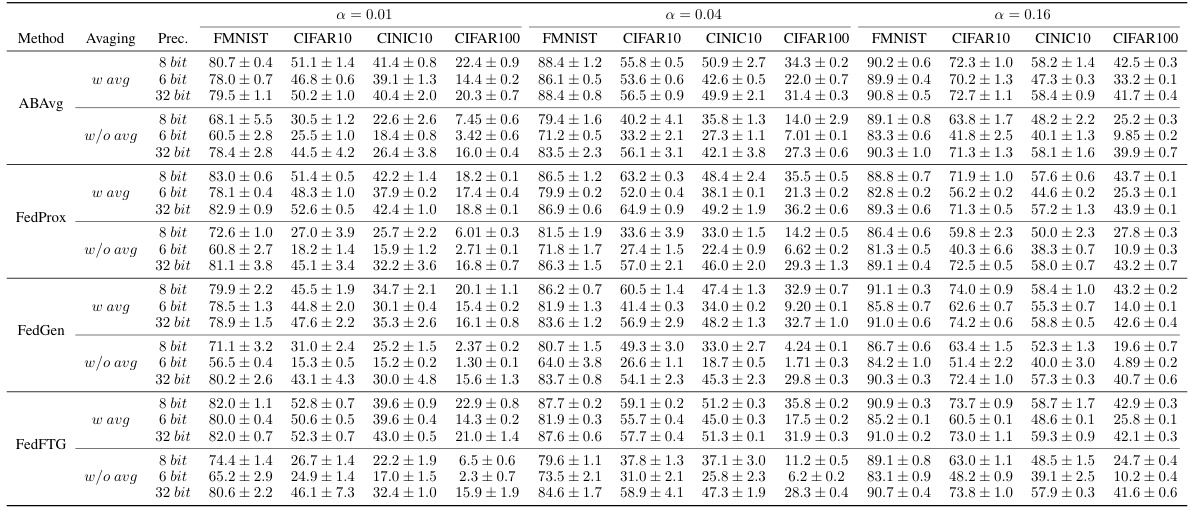
This table presents the results of the proposed low-precision federated learning method integrated with FedAvg. It shows the accuracy achieved with different levels of precision (32-bit, 8-bit, 6-bit) and data heterogeneity (α = 0.01, 0.04, 0.16). The results are compared with and without using moving average for model aggregation, demonstrating the effectiveness of the proposed approach, especially with 8-bit precision and moving average.
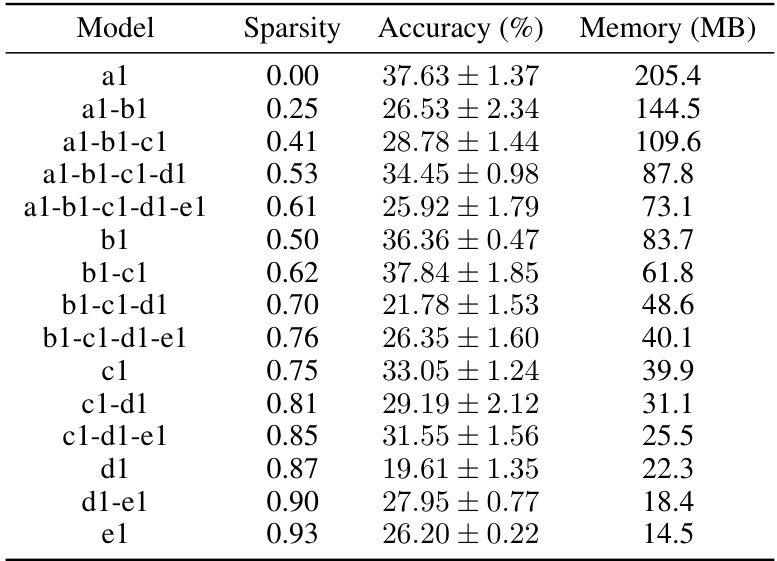
This table presents the results of experiments using the HeteroFL method. HeteroFL uses a variable number of model channels, represented by ‘Sparsity’. The table shows the accuracy achieved and the memory usage for different configurations of model channels. Each row shows the combination of model channels used, the resulting sparsity, the accuracy, and the memory usage (in MB). The results illustrate the trade-off between model size, sparsity, and accuracy. A smaller model (higher sparsity) results in lower memory usage but may also lead to lower accuracy.
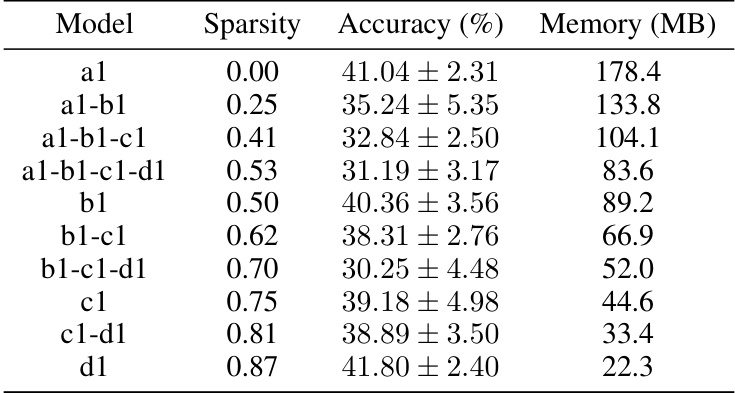
This table presents the results of experiments using the SplitMix model with a sparsity of 1/8. It shows the accuracy and memory usage for different model configurations, illustrating the trade-off between model size and performance. Different model configurations are tested, each with a varying number of model components trained in parallel. The results highlight how reducing the model size impacts the performance and memory requirements.

This table presents the results of using the SplitMix model compression technique with a compression ratio of 1/16 in federated learning. It shows the accuracy and memory usage for different model configurations, where the sparsity represents the fraction of the original model’s channels used. The parallel training indicates that multiple smaller models can be trained concurrently, leveraging available resources more efficiently.

This table presents the results of the proposed low-precision federated learning method integrated with FedAvg. It shows the accuracy achieved at different levels of precision (32, 8, and 6 bits) and data heterogeneity (represented by α), both with and without moving averaging in the server aggregation step. The results highlight that the low-precision approach with moving averaging maintains comparable performance to the full-precision approach even at 8 bits of precision, demonstrating its efficiency in computation and communication.
Full paper#



















