↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Multi-agent reinforcement learning (MARL) often employs parameter sharing to improve sample efficiency. However, the common approach of full parameter sharing often results in homogeneous policies, limiting performance. This homogeneity is a significant problem, especially when dealing with diverse agents or complex tasks requiring heterogeneous strategies. Addressing this limitation requires methods that balance sample efficiency with policy diversity.
Kaleidoscope tackles this problem by using learnable masks for adaptive partial parameter sharing. The model employs a single set of shared parameters along with multiple learnable masks for each agent. These masks control the parameter sharing dynamically, promoting policy heterogeneity among agents. The method also includes a novel regularization term to encourage diversity among policies and a resetting mechanism to prevent the network from becoming overly sparse. Extensive experiments show Kaleidoscope outperforms traditional parameter sharing approaches across various environments, suggesting its potential for improving MARL performance.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in multi-agent reinforcement learning (MARL) as it introduces a novel approach to address the critical limitation of homogeneous policies in parameter sharing. Kaleidoscope’s adaptive partial parameter sharing enhances both sample efficiency and policy diversity, opening up new research directions in this field. The method is empirically validated across diverse environments, proving its generalizability and effectiveness, which is essential for researchers seeking to enhance MARL systems performance.
Visual Insights#
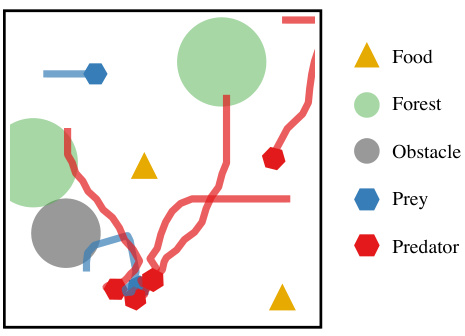
This figure shows an example of how full parameter sharing in multi-agent reinforcement learning leads to homogeneous policies. In a predator-prey scenario, all predators follow the same prey, ignoring other available options. This illustrates a key limitation of full parameter sharing: it prevents the development of diverse and potentially more effective strategies.
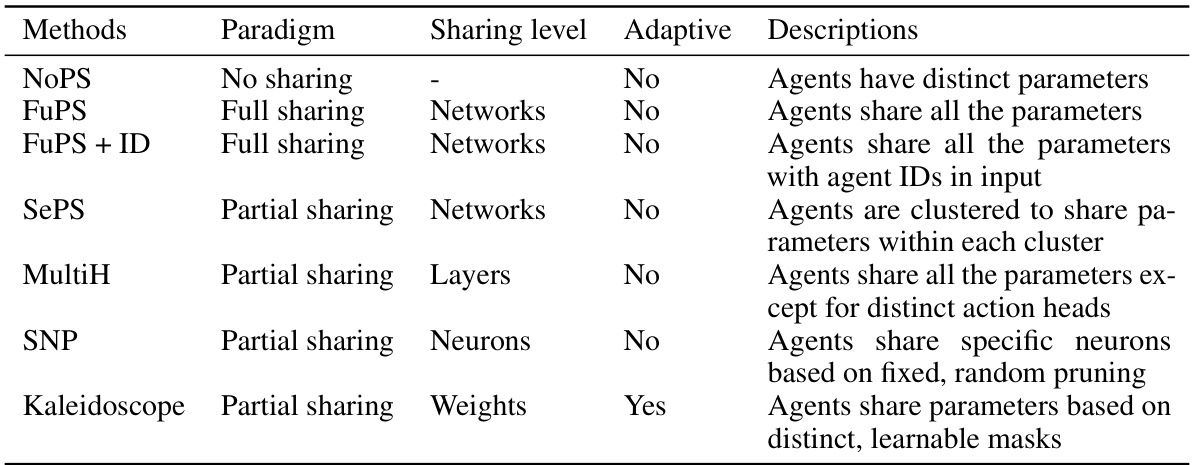
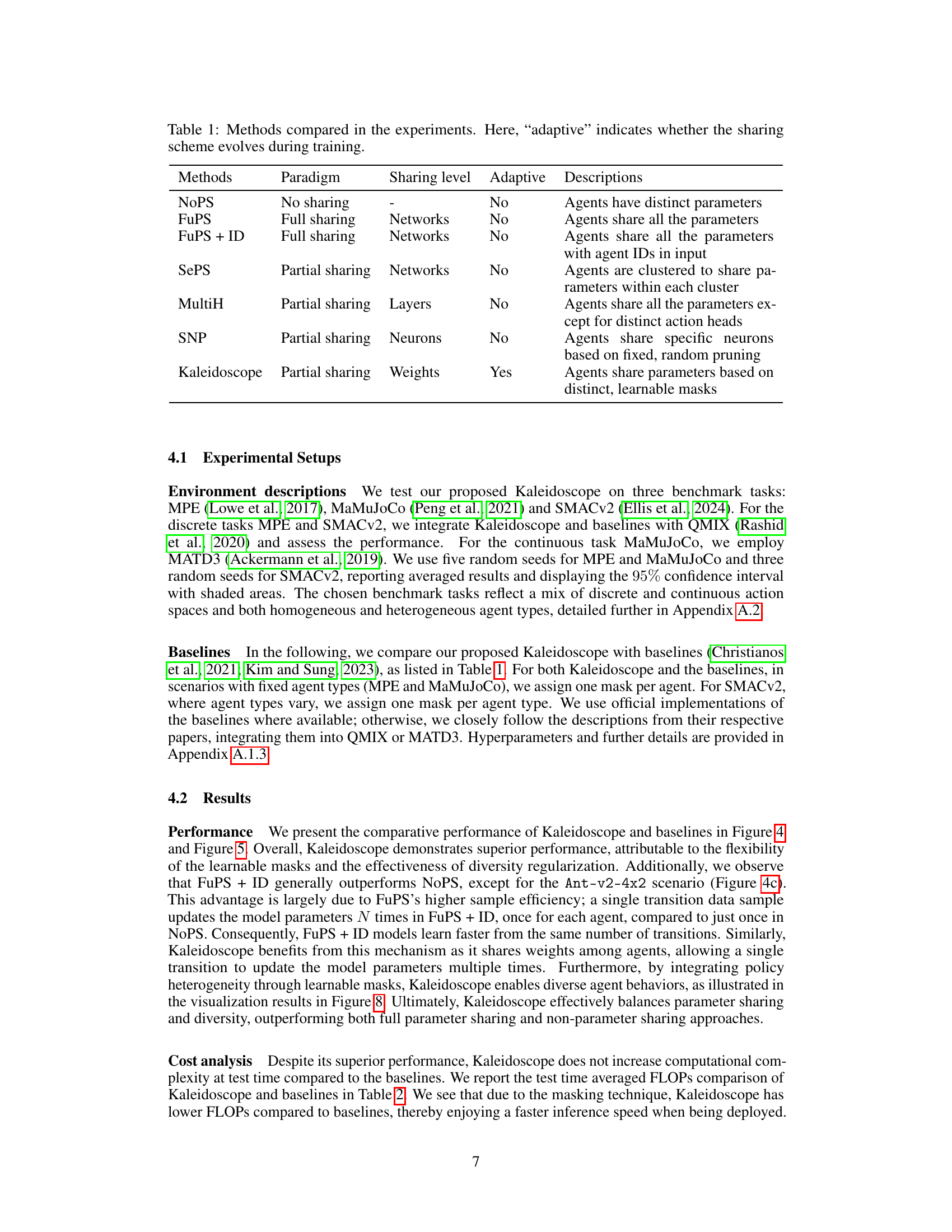
This table compares different multi-agent reinforcement learning (MARL) methods used in the paper’s experiments. Each method is categorized by its parameter sharing paradigm (no sharing, full sharing, or partial sharing), the level at which parameters are shared (networks, layers, neurons, or weights), whether the sharing scheme adapts during training, and a brief description of how parameters are shared. This helps to understand the various approaches to parameter sharing and their differences.
In-depth insights#
Learnable Masks#
The concept of “learnable masks” presents a novel approach to parameter sharing in multi-agent reinforcement learning (MARL). Instead of enforcing complete homogeneity through full parameter sharing or encountering the sample inefficiency of no sharing, learnable masks offer a dynamic, adaptive solution. These masks act as learned gatekeepers, selectively controlling which parameters are shared between agents, fostering heterogeneity while retaining high sample efficiency. The masks’ adaptability is key, allowing the model to dynamically adjust the level of parameter sharing based on environmental demands and the learning progress of individual agents. This contrasts with static methods which predefine sharing patterns, proving less effective across diverse scenarios. By incorporating a regularization term that encourages mask discrepancy, the system further promotes diversity among policies, while resetting mechanisms prevent network sparsity and mitigate potential bias. The flexibility and adaptability of learnable masks represent a significant step towards bridging the gap between full parameter sharing and complete independence in MARL, enabling more robust and effective training in heterogeneous multi-agent environments.
Adaptive Sharing#
Adaptive parameter sharing in multi-agent reinforcement learning (MARL) aims to balance the sample efficiency of full parameter sharing with the policy diversity of no parameter sharing. A key challenge is dynamically adjusting the level of parameter sharing based on environmental demands and agent learning progress. This adaptive approach contrasts with static methods that pre-define sharing schemes at the start of training. Learnable masks offer a promising solution by allowing the model to learn which parameters to share between agents. This dynamic adjustment enables the agents to develop diverse policies while still benefiting from the efficiencies of sharing. Furthermore, the adaptive nature of learnable masks allows for a flexible trade-off between sample efficiency and policy representation capacity, bridging the gap between homogeneous and heterogeneous strategies. Regularization techniques can encourage diversity amongst the learned policies, promoting better overall performance. However, adaptive methods necessitate careful consideration of potential issues like over-sparsity of network weights or unintended homogeneity, demanding novel solutions such as weight resetting mechanisms to maintain representational capacity and avoid bias.
Policy Diversity#
Policy diversity in multi-agent reinforcement learning (MARL) is crucial for achieving robust and high-performing systems. Homogeneous policies, where all agents adopt the same strategy, can lead to vulnerabilities and limit the overall team’s capability to adapt to complex situations. The paper explores the challenges of balancing the benefits of parameter sharing (improved sample efficiency) with the need for diverse policies, proposing a novel approach called Kaleidoscope. This method allows for adaptive partial parameter sharing, dynamically learning masks to regulate the sharing of parameters between agents. Learnable masks introduce heterogeneity by enabling agents to specialize in different aspects of the task, even while leveraging the efficiencies of shared weights. This approach moves beyond fixed or static parameter sharing schemes, enhancing the adaptability and performance of MARL agents in various environments. The success of Kaleidoscope hinges on the dynamic balance it achieves between homogeneity and heterogeneity. The core idea is to enable dynamic adjustment of parameter sharing during training, a key step in promoting diversity. It directly addresses the limitation of full parameter sharing approaches by allowing for a flexible balance of sample efficiency and diverse agent capabilities. Regularization techniques, such as pairwise distance maximization between masks, further encourage the development of distinct policies.
Critic Ensembles#
In multi-agent reinforcement learning (MARL), using a single critic network can lead to inaccurate value estimations, particularly in complex environments. Critic ensembles offer a robust solution by employing multiple critic networks, each learning a different value function. This approach enhances learning stability and mitigates the risk of overestimation bias, a common problem in MARL. However, training multiple critics can significantly increase computational costs and potentially lead to redundant value estimations if not properly regulated. To address these challenges, the paper proposes to enhance sample efficiency by sharing parameters across the critic ensemble. Instead of maintaining entirely separate networks, they dynamically learn shared parameters along with distinct learnable masks. This approach allows for balanced exploration of heterogeneous value functions while maintaining the benefits of parameter sharing. The proposed learnable masks regulate parameter sharing between the ensemble members, ensuring diversity without compromising sample efficiency or increasing computational demands too much. This adaptive parameter sharing is crucial for creating a powerful yet efficient system, capable of efficiently balancing exploration of diverse value functions with the need for high sample efficiency, ultimately leading to improved performance in MARL.
MARL Heterogeneity#
Multi-agent reinforcement learning (MARL) often struggles with the challenge of balancing efficient learning and diverse agent policies. Full parameter sharing, a common approach to boost sample efficiency, frequently leads to homogeneous agent behaviors, limiting overall performance. MARL heterogeneity addresses this by promoting diverse policies amongst agents, enabling more robust and adaptable solutions to complex, multi-agent tasks. This diversity can manifest in various ways, such as agents specializing in different subtasks, exhibiting diverse exploration strategies, or developing unique approaches to problem-solving. The trade-off between homogeneity (sample efficiency) and heterogeneity (policy diversity) is a key focus in MARL research. Achieving heterogeneity often requires careful design, sometimes employing techniques like partial parameter sharing, where agents share some but not all parameters, or learnable masks, which dynamically control parameter sharing during training. The key goal is to leverage the benefits of parameter sharing for sample efficiency while enabling sufficient agent-level distinctions to avoid performance bottlenecks associated with uniform behavior.
More visual insights#
More on figures
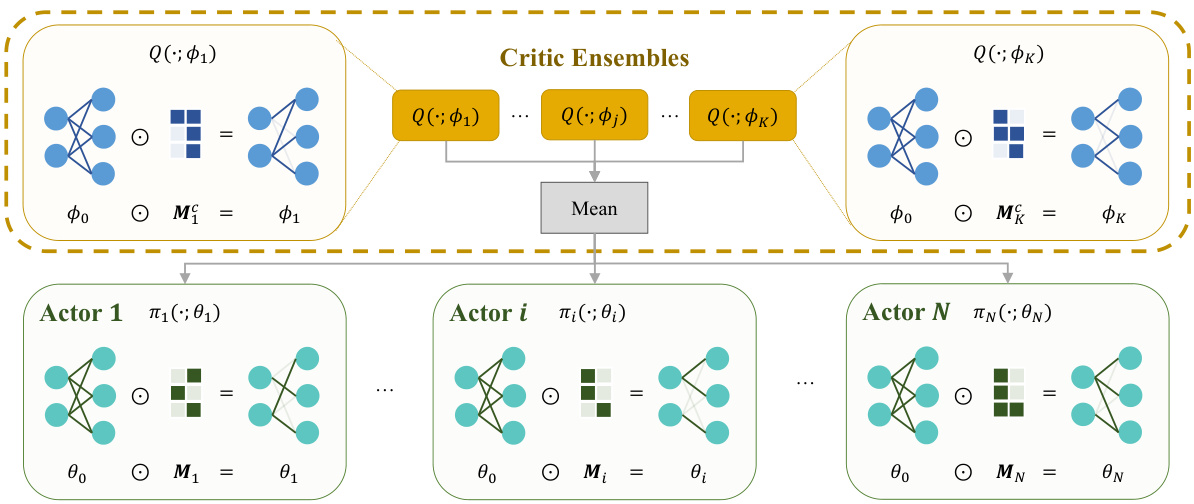
This figure illustrates the architecture of the Kaleidoscope model. It shows how a single set of parameters (θ₀ for actors, ϕ₀ for critics) is used across multiple agents. Each agent has a unique learnable mask (Mᵢ for actors, Mⱼ for critics) that selectively gates the shared parameters, allowing for heterogeneity in the policies and value estimations while maintaining high sample efficiency. The Hadamard product (⊙) combines the shared parameters with the agent-specific masks.
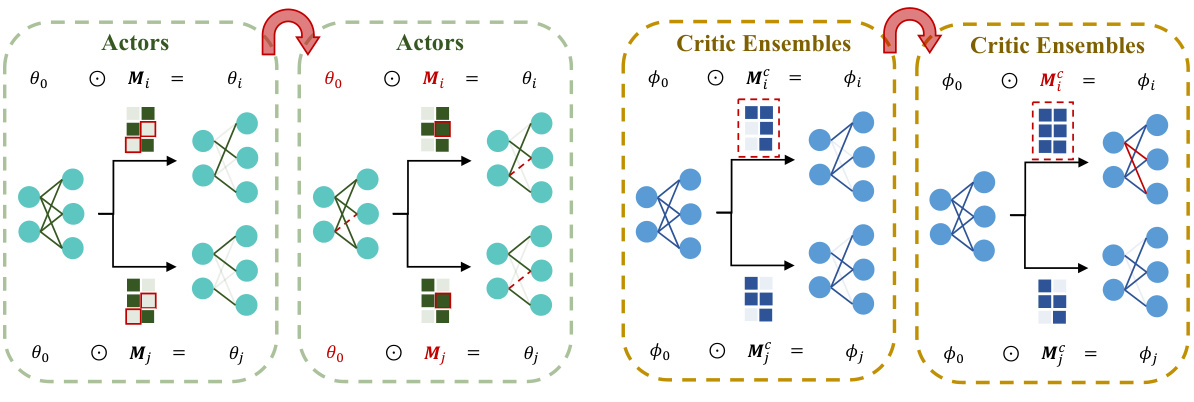
This figure illustrates the resetting mechanisms used in Kaleidoscope for both actor networks and critic ensembles. For actors, the weights masked by all agents are reinitialized with probability p, encouraging heterogeneity. For critic ensembles, one set of masks is reset at a time, promoting diversity among critic functions. The figure showcases how these resetting mechanisms prevent excessive sparsity and enhance the representational capacity of the network.

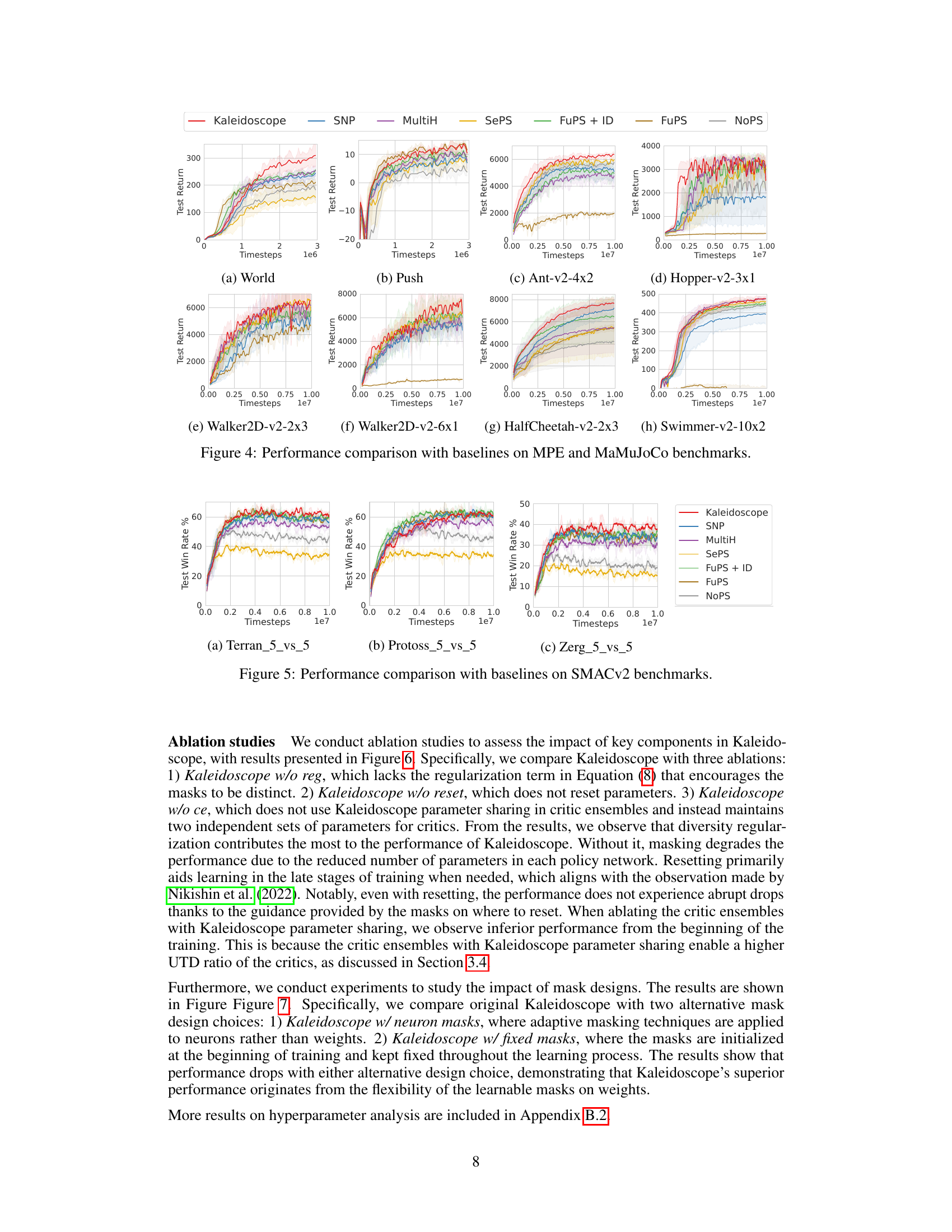
This figure presents a comparison of the performance of Kaleidoscope and several baseline methods across eight different scenarios from the Multi-Agent Particle Environment (MPE) and Multi-Agent MuJoCo (MaMuJoCo) benchmarks. Each subplot represents a different scenario, showing the average test return over training timesteps for each algorithm. The shaded areas represent 95% confidence intervals. The results demonstrate the superior performance of Kaleidoscope in most scenarios, highlighting its effectiveness in balancing sample efficiency and policy diversity.
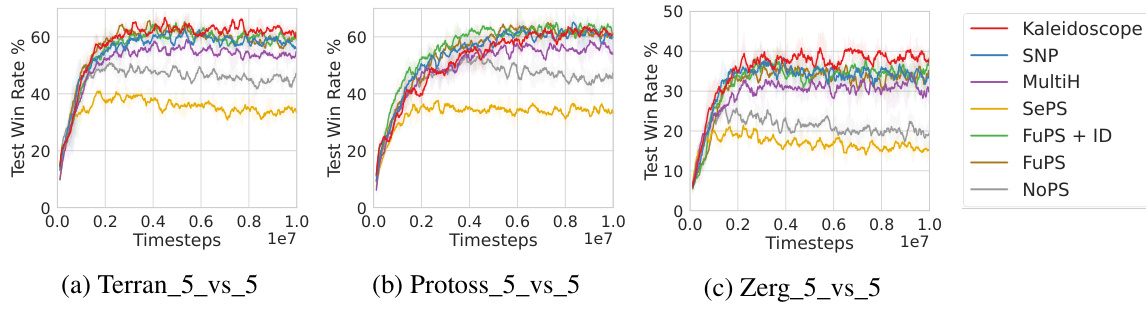
This figure compares the performance of Kaleidoscope against several baselines on three different StarCraft II scenarios (Terran_5_vs_5, Protoss_5_vs_5, and Zerg_5_vs_5). Each line represents the average test win rate over multiple runs for a particular algorithm. The x-axis shows the training progress (timesteps), and the y-axis shows the win rate. The figure visually demonstrates the superior performance of Kaleidoscope compared to other parameter sharing approaches across these complex multi-agent scenarios.
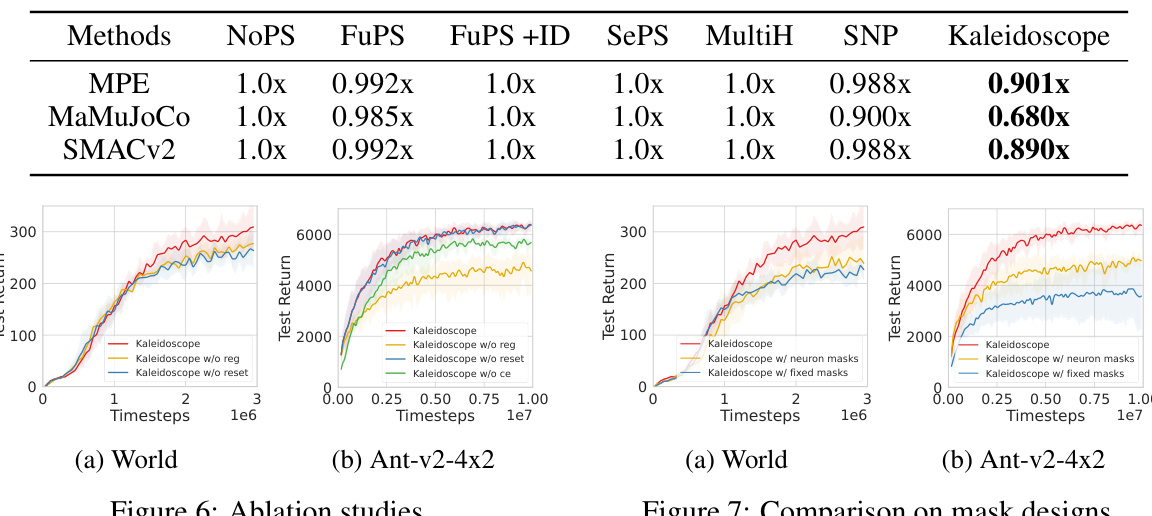
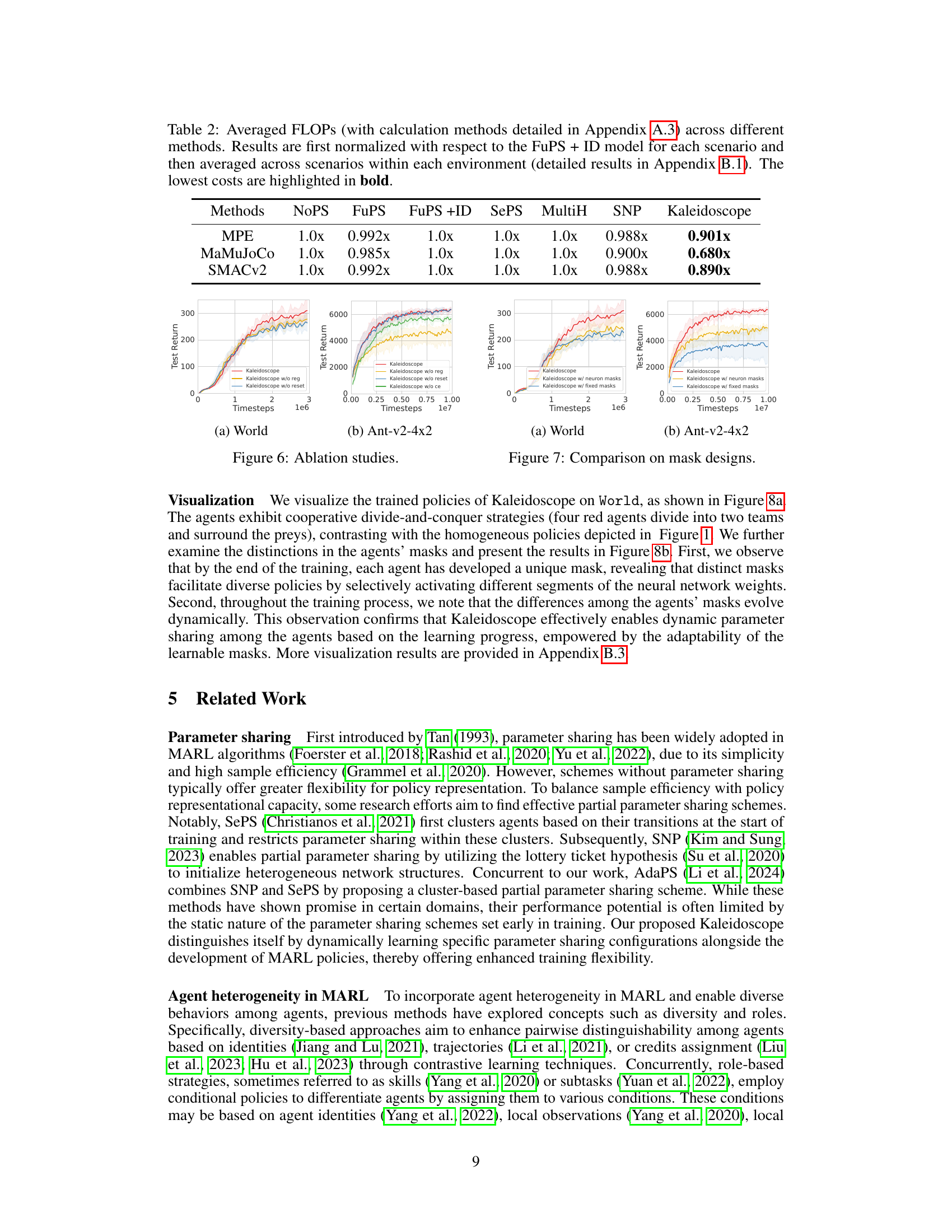
The ablation studies compare Kaleidoscope with three variations: one without the diversity regularization term, another without the parameter resetting mechanism, and a final version without critic ensembles using Kaleidoscope. The results show that the diversity regularization is crucial for Kaleidoscope’s performance, while the resetting mechanism offers additional benefits, particularly in later training stages. The use of critic ensembles with Kaleidoscope also contributes significantly to the overall results.
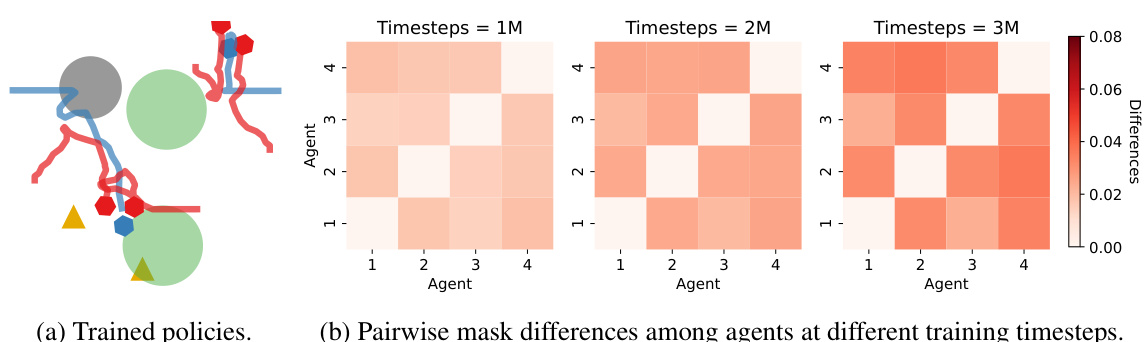
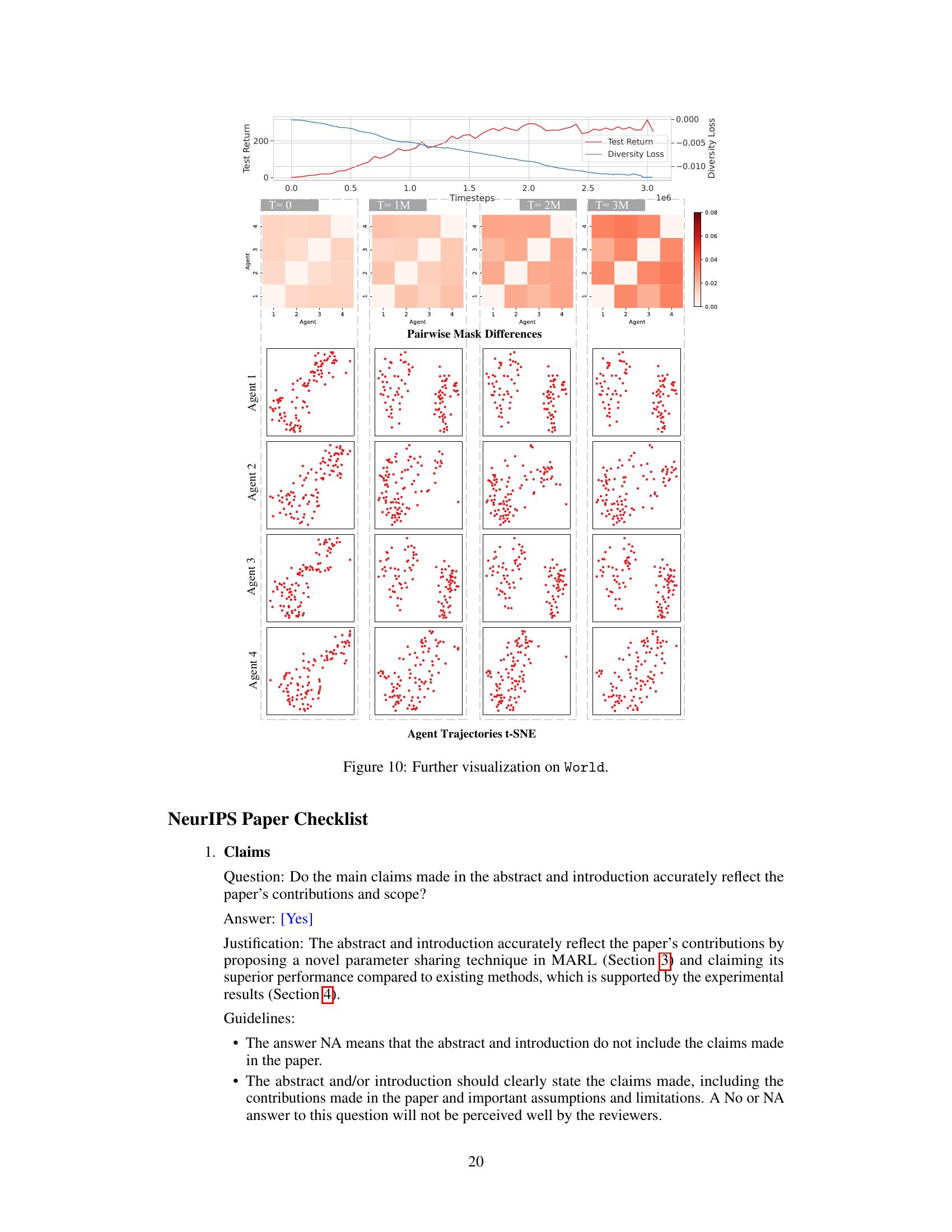
This figure visualizes the trained policies and pairwise mask differences among agents at different training timesteps in the ‘World’ scenario. (a) shows the trained policies, illustrating the agents’ strategies. (b) presents heatmaps showing the pairwise differences between agents’ masks at various training stages (1M, 2M, and 3M timesteps), highlighting how these differences evolve during training, indicating the development of distinct policies.
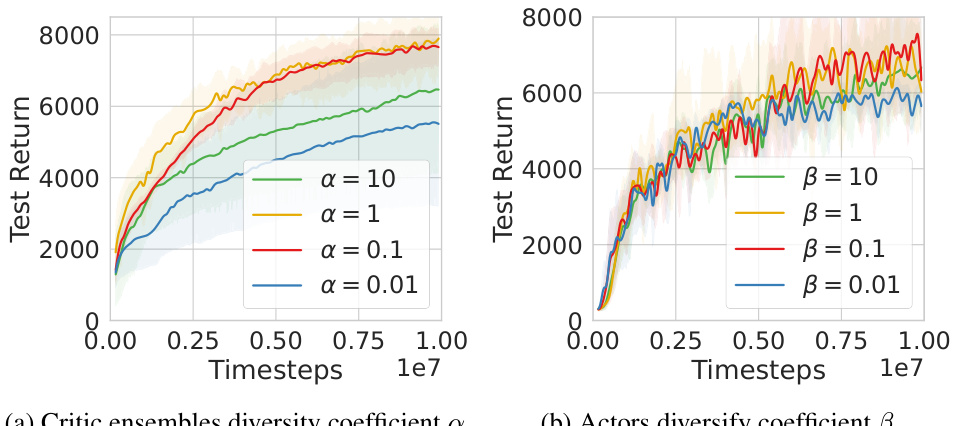
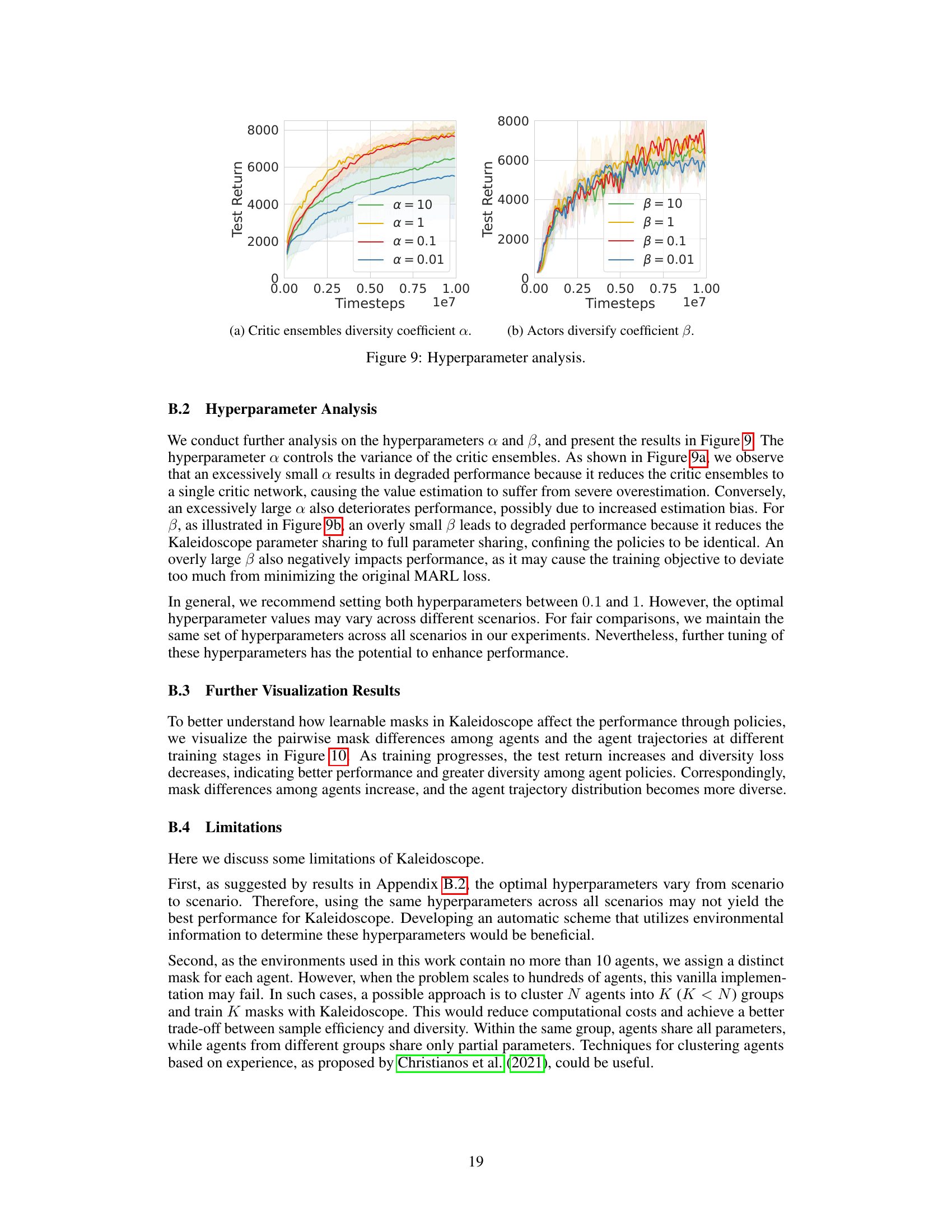
The plots show the impact of hyperparameters α (critic ensembles diversity coefficient) and β (actors diversity coefficient) on the performance of Kaleidoscope. The left plot shows that an excessively small α leads to degraded performance due to the critic ensembles collapsing to a single critic, while an excessively large α also degrades performance due to increased estimation bias. The right plot shows that a small β leads to degraded performance because Kaleidoscope’s parameter sharing reduces to full parameter sharing, causing policy homogeneity. An excessively large β also negatively impacts performance. Optimal performance is achieved with α and β values between 0.1 and 1.
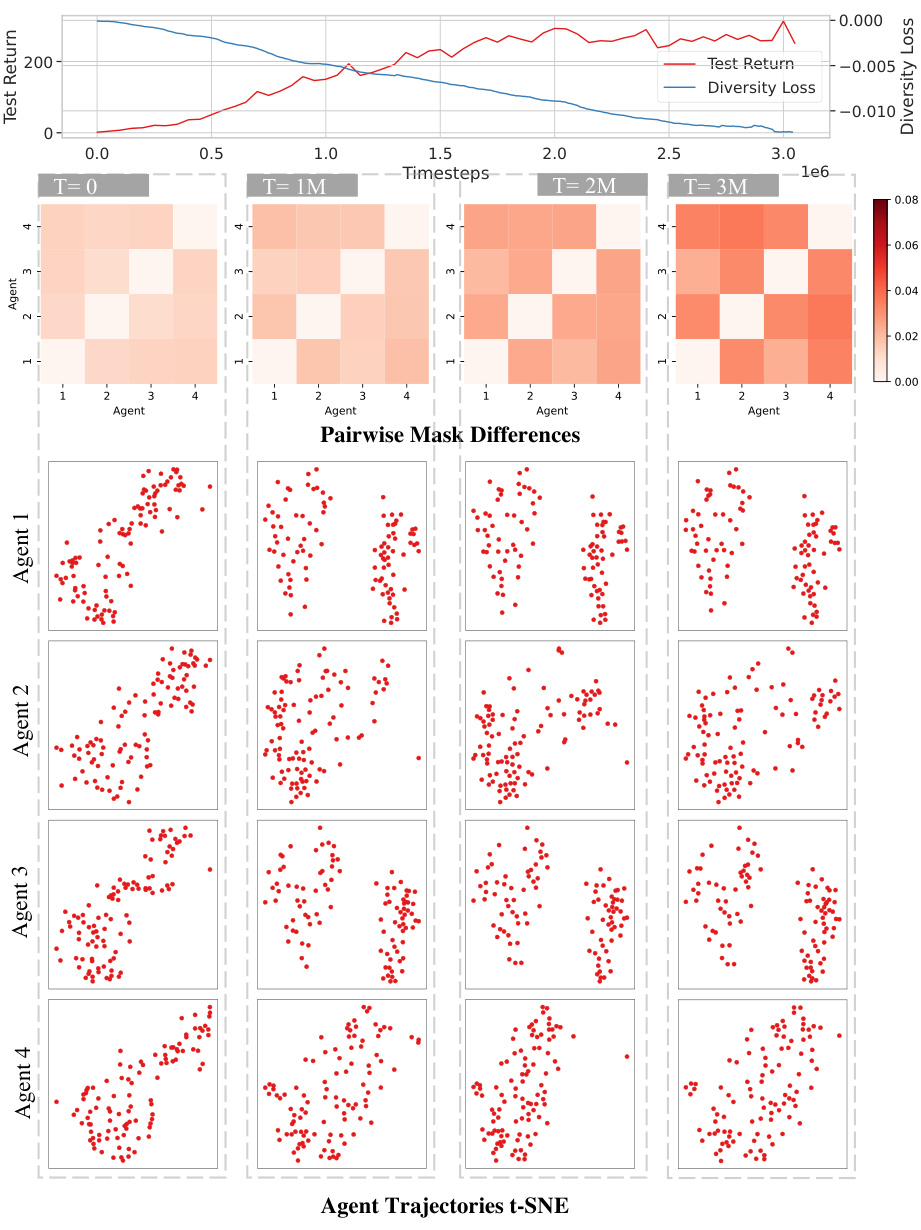
This figure visualizes the trained policies of Kaleidoscope on the ‘World’ environment at different training timesteps (1M, 2M, 3M). The top panel shows the test return and diversity loss curves over time. The middle panel displays heatmaps representing pairwise mask differences between agents at different timesteps. The bottom panel uses t-SNE to visualize the trajectories of each agent. The visualizations demonstrate how Kaleidoscope dynamically learns to share parameters (as indicated by the evolving mask differences) and how this leads to diverse and effective agent policies (as seen in their distinct trajectories).
More on tables

This table lists the common hyperparameters used for the MATD3 algorithm in the MaMuJoCo domain experiments. It includes the number of layers in the neural network, the size of the hidden layers, the discount factor, the number of rollout threads, the learning rate for the critic and actor networks, exploration noise, batch size, replay buffer size, total number of environment steps, and the n-step parameter for the algorithm. These parameters are crucial in setting up the training process and significantly influence the results of the experiments.

This table lists the common hyperparameters used for the QMIX algorithm in the Multi-agent Particle Environment (MPE) domain. It includes parameters such as the number of layers in the neural network, hidden layer sizes, discount factor, learning rate, exploration noise parameters (initial and final epsilon values), batch size, replay buffer size, number of training steps, and whether or not Double Q-learning is used.

This table shows the common hyperparameters used when applying the QMIX algorithm in the Multi-agent Particle Environment (MPE) domain. The hyperparameters listed are those used for all algorithms and baselines used in the experiment and include the number of layers in the neural network, the hidden layer sizes, the discount factor (gamma), the learning rate, the initial and final exploration rates (epsilon), the batch size, the replay buffer size, the number of environment steps, and whether the Double Q learning technique was used.

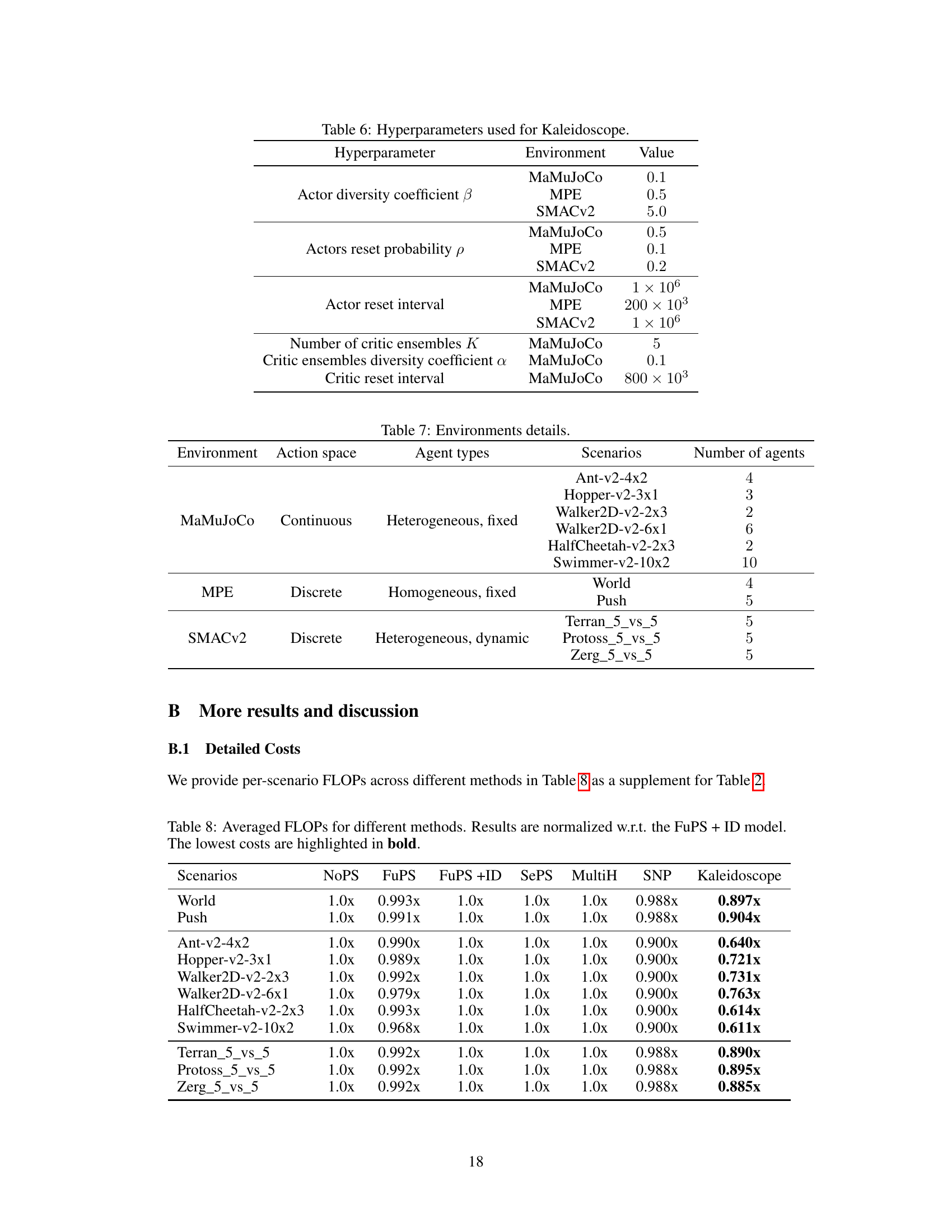
This table lists the hyperparameters used in the Kaleidoscope model, categorized by environment (MaMuJoCo, MPE, and SMACv2) and hyperparameter type (actor diversity coefficient, actor reset probability, actor reset interval, number of critic ensembles, critic ensembles diversity coefficient, and critic reset interval). Each hyperparameter’s value is specified for each environment, demonstrating the model’s adaptability to different experimental settings.
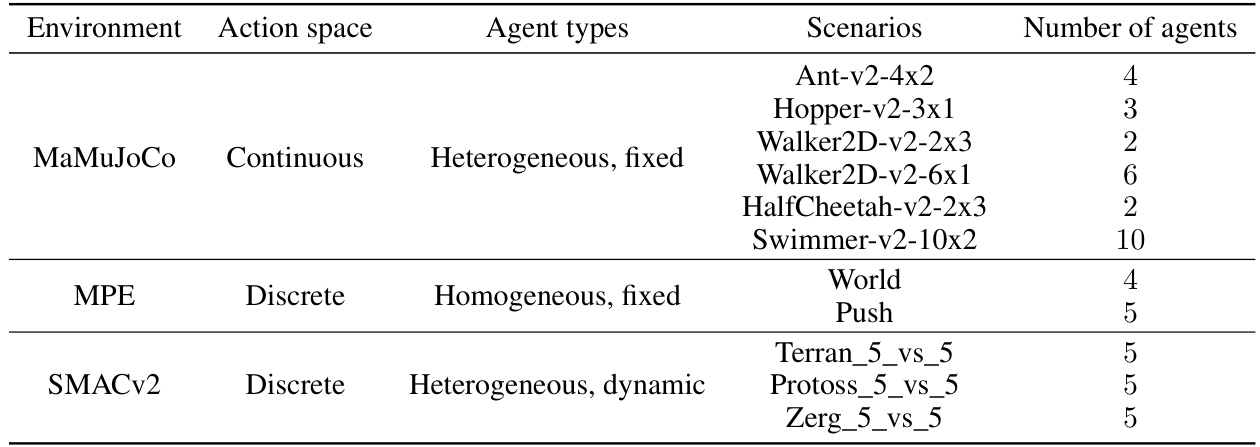
This table lists the experimental environments used in the paper. It includes the environment name (MaMuJoCo, MPE, SMACv2), action space type (continuous or discrete), agent types (homogeneous or heterogeneous), specific scenarios used within each environment and the number of agents involved in each scenario.
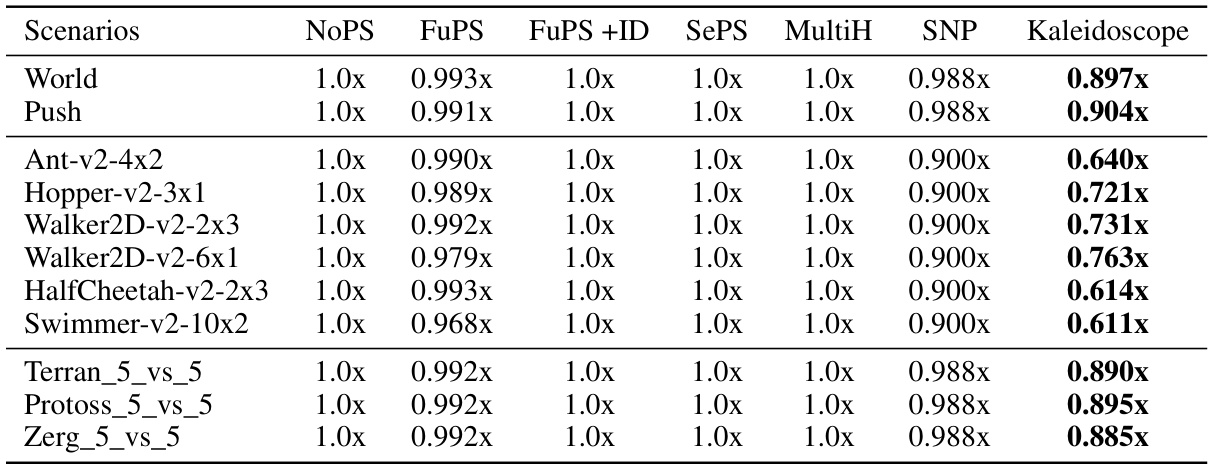
This table compares the computational cost (measured in FLOPs) of different multi-agent reinforcement learning methods. The FLOPs are normalized relative to the ‘FuPS + ID’ method for each scenario and then averaged across scenarios within each environment. The lowest FLOPs for each environment are highlighted in bold, indicating the most computationally efficient methods.
Full paper#