High Rank Path Development: an approach to learning the filtration of stochastic processes

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is vital for researchers working with stochastic processes, particularly in finance and economics. It introduces a novel metric and algorithm that efficiently addresses the limitations of existing methods for characterizing stochastic processes, including the crucial aspect of information flow over time. This opens new avenues for generative modeling of time series data and solving classic problems in optimal stopping and utility maximization. The work is significant due to its strong theoretical foundations and impressive empirical results, demonstrated by outperforming several state-of-the-art methods.

Visual Insights

#

This figure illustrates the high-rank path development method. It starts with a stochastic process X and its filtration F. The prediction process Xt, representing the conditional distribution of X given the filtration at time t, is then calculated. The Path Characteristic Function (PCF), Φλ,(M₁), which is a function of the prediction process, is computed. Finally, the high-rank development, UM₁,M₂(X), which captures higher-order information about the path, is obtained by applying a linear map M₂ to the PCF.

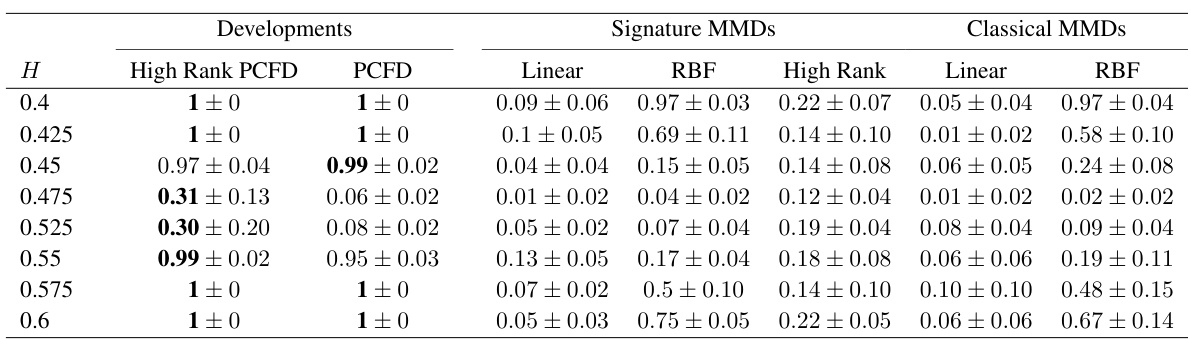
This table presents the results of a hypothesis testing experiment comparing the performance of different methods for distinguishing between two stochastic processes (3D Brownian motion and 3D fractional Brownian motion). The methods are High Rank PCFD, PCFD, linear and RBF signature MMDs, linear and RBF classical MMDs, and High Rank signature MMDs. The Hurst parameter H, which ranges from 0.4 to 0.6, is used to control the degree of long-range dependence. The test power, representing the probability that the method correctly rejects the null hypothesis (that the two processes are identical), is reported as the mean and standard deviation over 5 runs. Optimal hyperparameters for some of the methods were determined through a grid search.

In-depth insights

#

HRPCFD: A New Metric

#

The proposed HRPCFD (High Rank Path Characteristic Function Distance) metric offers a novel approach to measuring distances between stochastic processes, addressing limitations of traditional weak convergence methods. HRPCFD directly incorporates the filtration of the processes, a crucial aspect ignored by weak convergence that is vital for modeling time-dependent information flows. This is achieved using a clever combination of high rank path development from rough path theory and path characteristic functions. The method’s effectiveness lies in its ability to capture the differences in the evolution of conditional distributions of the processes over time. HRPCFD demonstrates favorable analytical properties, such as the characteristicity of synonymous processes and continuity, making it a theoretically sound and computationally practical alternative for applications requiring precise characterizations of stochastic processes, particularly in financial modeling and multi-period decision-making problems. The outperformance against several state-of-the-art metrics in numerical experiments further validates HRPCFD’s practical value. However, further investigation is needed to explore its robustness under various data conditions and its scalability to high-dimensional data.

High-Rank Path Dev.

#

The heading “High-Rank Path Development” suggests a novel approach within a framework that likely involves high-dimensional data and complex relationships, possibly using concepts from rough path theory. The “High-Rank” aspect likely refers to a method of representing or processing data using higher-order features or structures compared to traditional approaches. This may involve extending existing techniques to capture more nuanced information from sequential data or stochastic processes. Path Development probably entails constructing a representation of the data that highlights temporal dependencies and captures the evolution of information over time. This could involve techniques like signature computation or similar methods which unfold information progressively. The combination of high-rank features and path development suggests a more comprehensive approach to analyzing and learning intricate patterns in data, potentially leading to improved accuracy or more robust models, especially when dealing with noisy or incomplete data. The overall goal appears to be learning more about the underlying stochastic processes by expanding on traditional methods to capture the intricate dynamics.

HRPCF-GAN: Model

#

The heading “HRPCF-GAN: Model” suggests a generative adversarial network (GAN) architecture specifically designed for time series generation, leveraging a novel metric called the High Rank Path Characteristic Function Distance (HRPCFD). HRPCF-GAN likely employs the HRPCFD as its discriminator, differentiating it from traditional GANs which typically use simpler metrics. This choice is crucial because HRPCFD is designed to address the limitations of traditional weak convergence approaches for stochastic processes, offering improved sensitivity to the underlying filtration of time series data. The generator component would then learn to produce synthetic time series that can fool the HRPCFD discriminator, effectively learning the complex temporal dependencies inherent in real-world time series. The use of “high rank” in the name implies a sophisticated method for handling the complex structure of time series, possibly using higher-order path information or advanced feature extraction techniques. Overall, the HRPCF-GAN model presents an innovative approach to time-series generation, potentially overcoming previous limitations and achieving state-of-the-art performance in applications requiring accurate representation of temporal dynamics and information flow.

Extended Weak Conv.

#

Extended weak convergence offers a more robust approach to comparing stochastic processes than traditional weak convergence by explicitly considering the underlying filtration. This is crucial because the filtration reflects the information flow over time, which is often ignored by standard weak convergence. The implications are profound; models that are “close” in the weak topology might be vastly different in practice when multi-period decisions are involved (e.g., pricing American options). Extended weak convergence addresses this by focusing on the convergence of conditional distributions of the process given the filtration at each time point. Consequently, it provides continuity for value functions in problems involving multi-period decisions, such as optimal stopping or utility maximization problems, where the flow of information is essential. While computationally challenging, the development of new metrics and efficient algorithms based on extended weak convergence represents significant progress in addressing the limitations of classical weak convergence and allows for the study of stochastic processes with a greater emphasis on temporal and informational dynamics.

Future Research

#

The paper’s “Future Research” section would ideally explore several avenues. Extending the HRPCF-GAN’s applicability to other data types beyond the financial time series used in the experiments is crucial to demonstrate broader utility. Investigating the impact of different network architectures on the filtration learning process could refine the model and lead to improved performance. A rigorous theoretical analysis of HRPCFD’s convergence properties is needed for a deeper understanding and potential improvements. Additionally, exploring the computational cost and scalability of the methods, especially for high-dimensional data, is essential. Addressing the challenge of accurately estimating conditional probability measures in more complex scenarios is paramount for practical applications. Finally, comparisons with other adapted weak topology metrics and exploration of applications to challenging multi-period optimization problems would solidify its impact in addressing real-world challenges.

More visual insights

#

More on figures

This figure illustrates the architecture of the HRPCF-GAN, a generative adversarial network for learning the conditional distribution of future time series given past data. It shows how the generator (Ge), which produces synthetic future paths, and the discriminator (HRPCFD), based on the High Rank Path Characteristic Function Distance, interact. The discriminator evaluates the similarity between real and generated data based on the HRPCFD, which incorporates information about the filtration of the stochastic processes. The process involves multiple stages, including training regression models to estimate conditional probability measures and employing both PCFD and HRPCFD in the process of optimization.

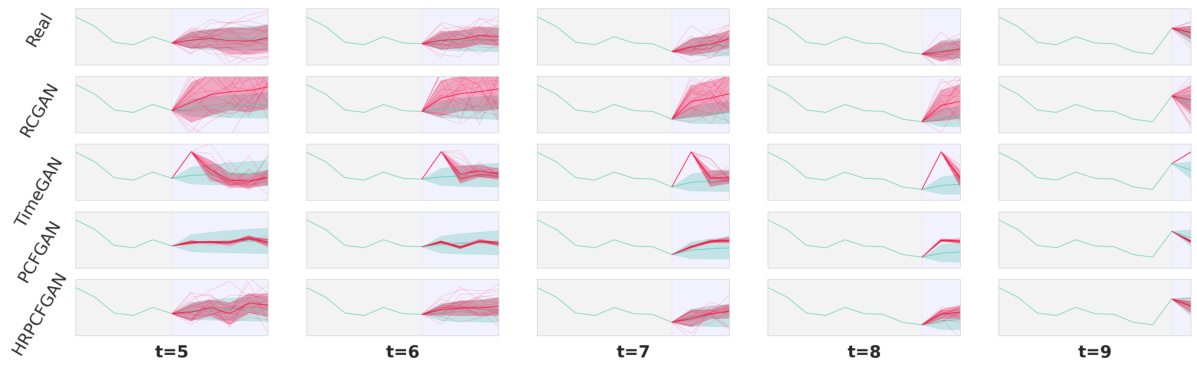
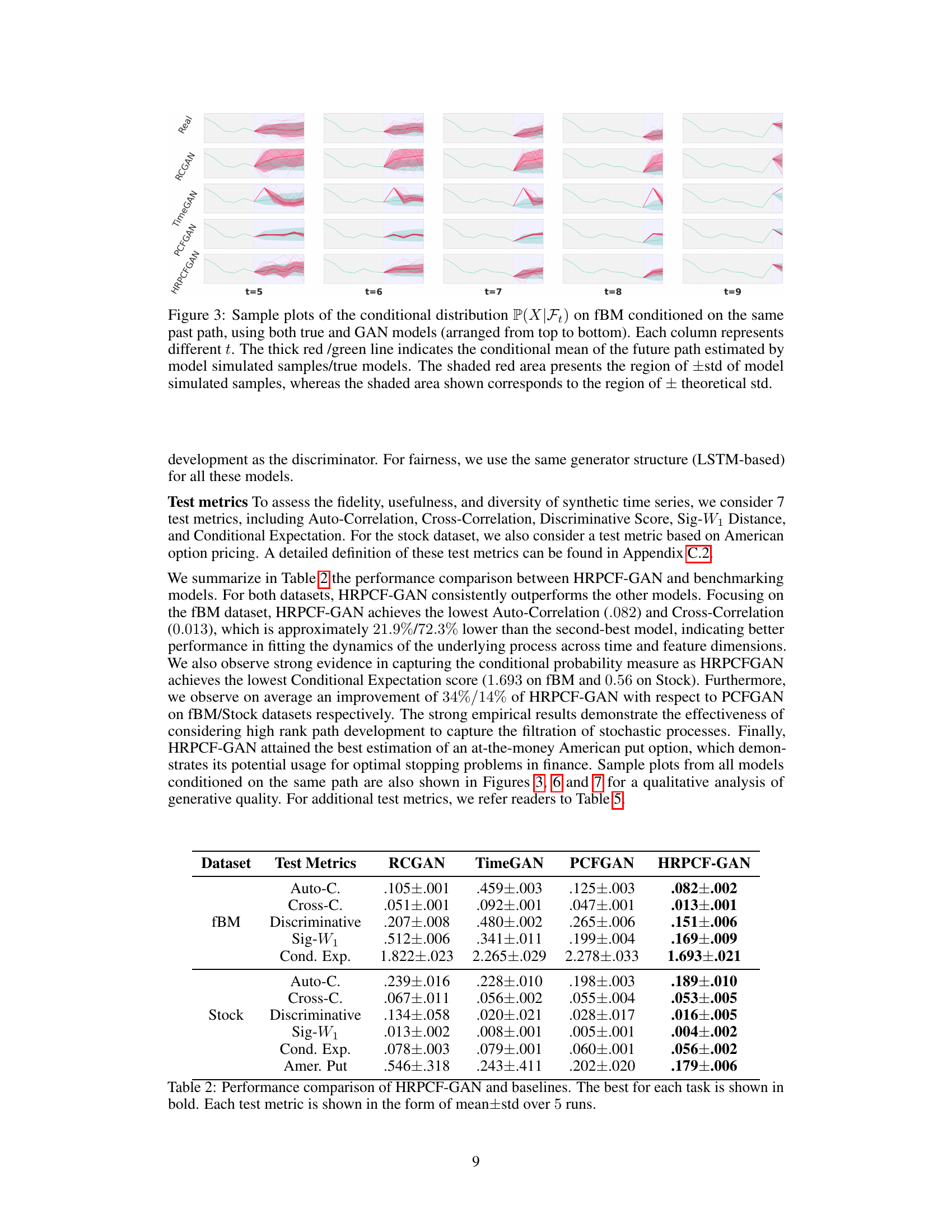
This figure compares the conditional distribution of future paths predicted by four different generative models (RCGAN, TimeGAN, PCFGAN, and HRPCFGAN) with the true distribution for a fractional Brownian motion (fBM). Each column shows the distributions at a different time point (t). The red lines show the conditional mean predicted by the generative models, with shaded areas representing their standard deviations. The green lines show the true conditional means and standard deviations. The figure demonstrates the performance of different models in capturing the conditional probability distribution over time.

This figure illustrates the high-rank path development method. It shows how the prediction process, representing the conditional distribution of the stochastic process given its filtration, is used to construct a high-rank path characteristic function (HRPCF). This involves two steps: first, computing the PCF of the prediction process; then, applying a high-rank development to this PCF, resulting in a more informative representation of the process that captures the underlying filtration.

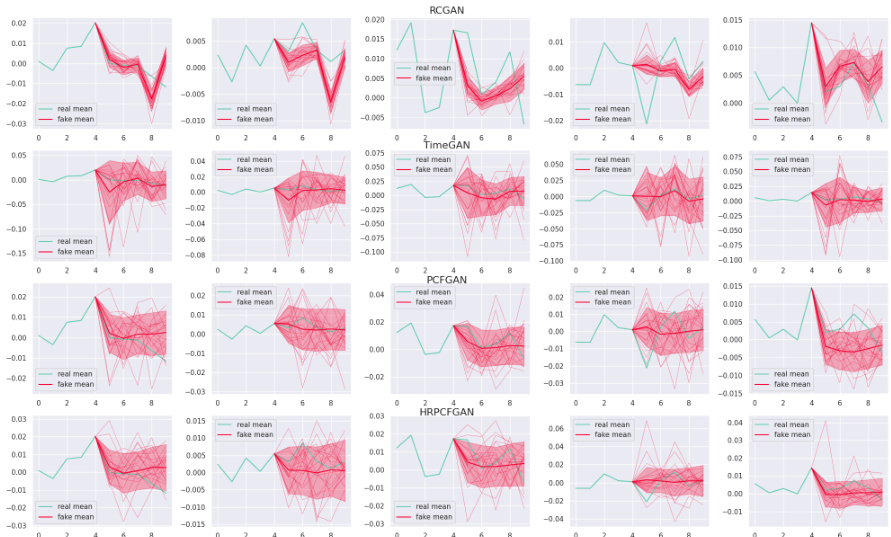
The figure shows the distributions of EPCFD and EHRPCFD under the null hypothesis (H0) and alternative hypothesis (H1) for a Hurst parameter of 0.475. The histograms illustrate the separation of the two distributions under the different hypothesis, demonstrating the effectiveness of both metrics in distinguishing between the two scenarios. Specific hyperparameter settings (K1, n, K2, m) used for each metric are provided in the caption.

This figure illustrates the high-rank path development method. It shows how the prediction process, represented as conditional distributions P(X|Ft) over time, is transformed using the Path Characteristic Function (PCF). The PCF, Φλ(M₁), captures the distribution’s characteristics. Then, a high-rank development, UM₁,M₂(X), further refines this representation by applying a linear map M₂ to the PCF path. This process allows for the incorporation of information about the filtration into a computable distance metric.

This figure illustrates the high-rank path development method. It shows how the prediction process, representing the conditional distribution of the stochastic process given its filtration up to time t, is used to construct the high-rank path characteristic function (HRPCF). The HRPCF is a key element in the proposed High Rank PCF Distance (HRPCFD) metric, which allows for efficient numerical implementation and is used to learn the filtration of stochastic processes. The figure depicts two steps of development: First, computing the PCF of the prediction process, and second, applying a higher-rank development to the PCF, resulting in the HRPCF.

More on tables

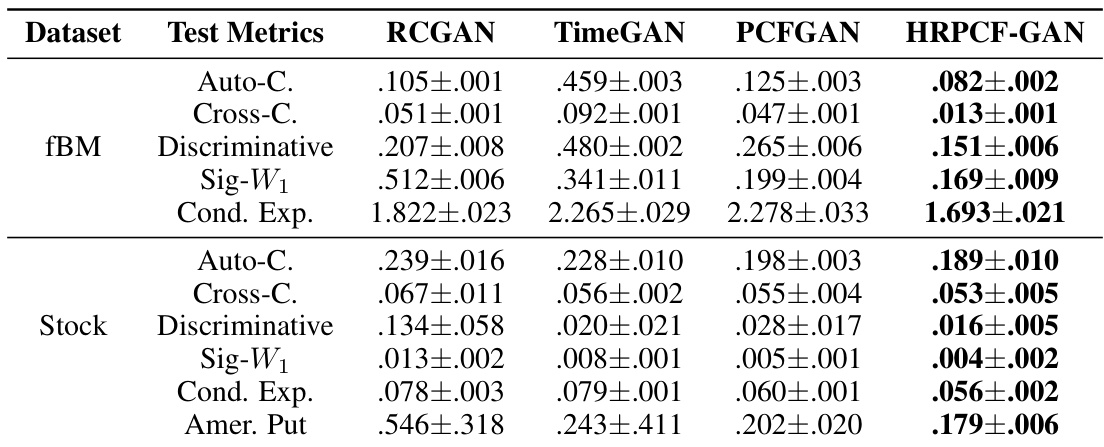
This table compares the performance of the HRPCF-GAN model against several baseline models (RCGAN, TimeGAN, PCFGAN) across seven evaluation metrics. The metrics assess different aspects of time series generation quality, including the fidelity of the generated series’ distribution, its correlation structure, and its ability to capture the conditional distribution. Two datasets were used for evaluation: a synthetic multivariate fractional Brownian motion dataset and a real-world stock market dataset. HRPCF-GAN demonstrates superior performance across most metrics and datasets.

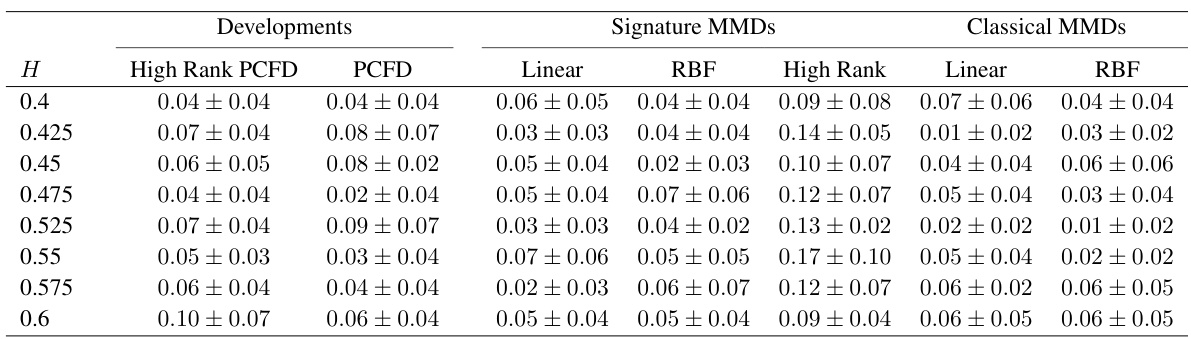
This table presents the results of hypothesis testing for different stochastic processes. The test power, representing the probability of correctly rejecting the null hypothesis (that the processes have the same distribution), is shown for various methods (High Rank PCFD, PCFD, Linear/RBF Signature MMDs, Linear/RBF Classical MMDs). The values are the mean ± standard deviation across 5 runs, and optimal hyperparameters for some methods are specified.

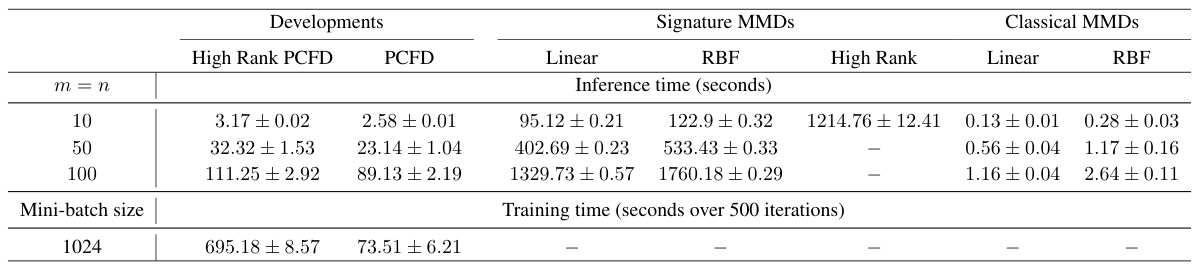
This table presents the statistical power of different distance metrics (High Rank PCFD, PCFD, Linear Signature MMD, RBF Signature MMD, High Rank Signature MMD, Linear Classical MMD, RBF Classical MMD) in distinguishing between 3-dimensional Brownian motion and 3-dimensional fractional Brownian motion with varying Hurst parameters (H). The power represents the probability of correctly rejecting the null hypothesis (that the processes are the same) when the alternative hypothesis (that the processes are different) is true. Different optimal parameters were used for the RBF and High Rank signature MMDs.

This table presents a comparison of the performance of HRPCF-GAN against other state-of-the-art models for time series generation on two datasets: a synthetic dataset (fBM) and a real-world stock market dataset. Seven metrics are used to evaluate the models’ performance, encompassing aspects such as fidelity (e.g., auto-correlation), diversity (ONND), and conditional expectations. HRPCF-GAN consistently shows superior performance across multiple evaluation metrics on both datasets.

This table compares the performance of HRPCF-GAN against three other baseline models (RCGAN, TimeGAN, PCFGAN) across seven evaluation metrics. The metrics assess various aspects of the generated time series, including autocorrelation, cross-correlation, discriminative ability, distance to real data, conditional expectation, and the accuracy in predicting options pricing. Results are reported for two datasets: a synthetic fractional Brownian motion dataset and a real-world stock market dataset. The best-performing model for each metric is highlighted in bold.

Full paper

#