↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Dimensionality reduction is crucial in machine learning, and the Johnson-Lindenstrauss Lemma provides strong theoretical guarantees using randomized projections. However, these methods ignore data structure. This paper explores using optimization to find low-distortion embeddings directly from data, addressing the non-convexity challenge of the distance-preserving objective. Existing derandomization methods for the JL lemma often rely on less direct techniques.
The authors propose a novel method using optimization over a larger space of random solution samplers. By gradually reducing the variance of the sampler, the method converges to a deterministic solution that avoids bad stationary points and satisfies the Johnson-Lindenstrauss guarantee. This optimization-based approach can be viewed as a derandomization technique and potentially applied to other similar problems. The paper includes theoretical analysis and experimental results supporting the effectiveness of their method.
Key Takeaways#
Why does it matter?#
This paper is important because it challenges the conventional wisdom in dimensionality reduction by demonstrating that optimization, rather than randomization, can achieve the same theoretical guarantees as the Johnson-Lindenstrauss Lemma. This opens new avenues for research in derandomization techniques and optimization-based approaches to embedding problems. The framework presented provides a solid foundation for future work in this area and has potential implications for various machine learning applications.
Visual Insights#

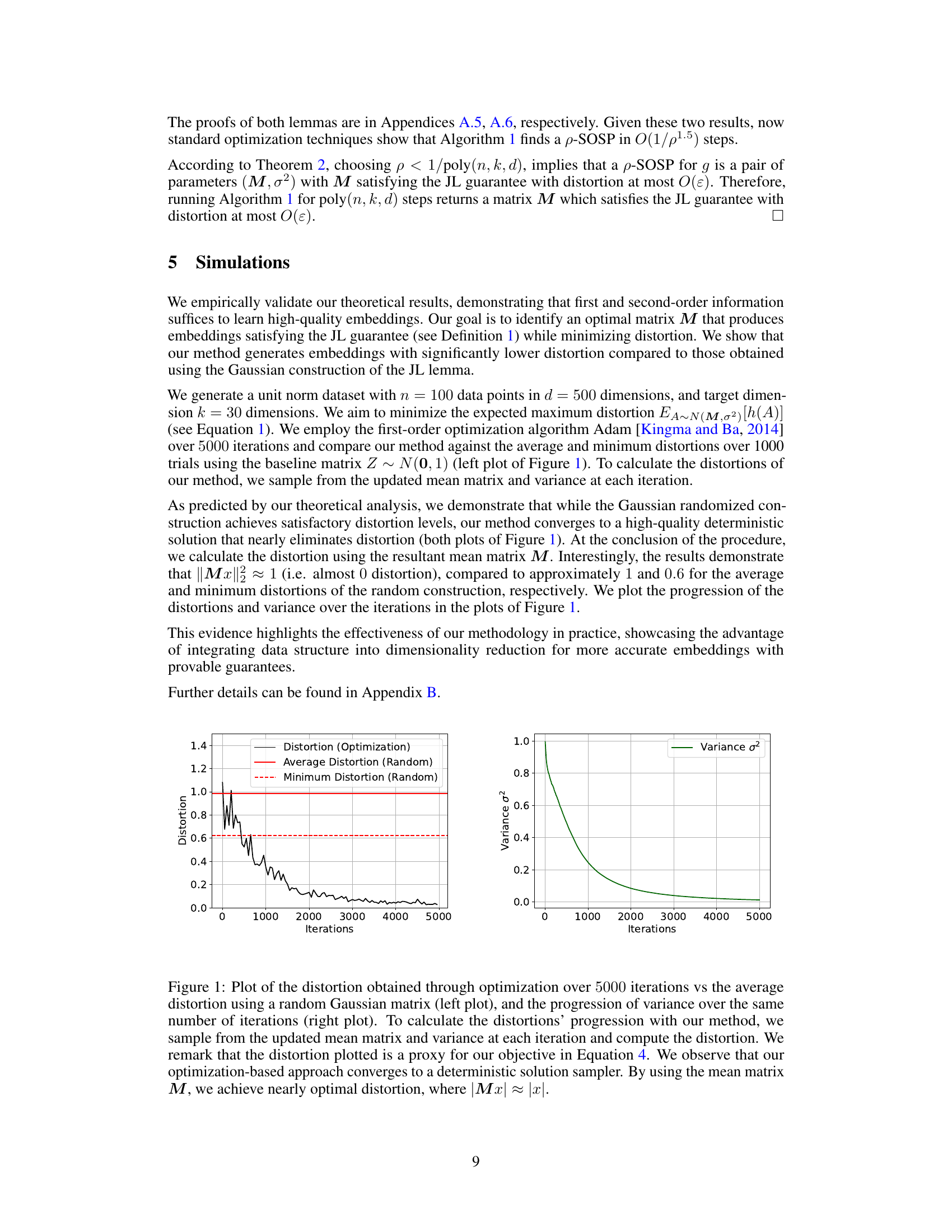
This figure shows the results of a simulation comparing the performance of the proposed optimization-based method for finding Johnson-Lindenstrauss embeddings against a standard randomized approach using Gaussian matrices. The left plot shows the maximum distortion over iterations, comparing the optimization method (black line) with the average and minimum distortions obtained using random matrices (red and dashed red lines). The right plot shows the decrease in variance of the Gaussian sampler across the iterations of the optimization process. The optimization method demonstrates that it is able to achieve near-optimal distortion as the variance tends to zero and converges to a deterministic solution.

This figure shows two plots. The left plot compares the distortion obtained using the proposed optimization-based method over 5000 iterations with the average and minimum distortion obtained using a random Gaussian matrix. The right plot illustrates how the variance of the Gaussian distribution changes over the 5000 iterations. The results demonstrate that the proposed method converges to a deterministic solution sampler, achieving near-optimal distortion.
Full paper#