↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Existing methods for verifying relational properties of Deep Neural Networks (DNNs) suffer from imprecision due to ignoring dependencies between multiple executions or lacking efficient branching strategies. This leads to unreliable verification results, especially in safety-critical applications where robustness against adversarial attacks is paramount. The inability to reason about these dependencies hinders the development of truly trustworthy AI systems.
This paper introduces RABBit, a novel Branch-and-Bound based verifier that addresses these limitations. RABBit efficiently combines branching strategies over multiple executions with a cross-executional bounding method, effectively leveraging dependencies between DNN outputs. The resulting MILP instance is efficiently solved, providing substantial precision improvements over existing state-of-the-art methods. RABBit’s superior performance is demonstrated through extensive experiments on diverse datasets and network architectures, proving its practical relevance in ensuring the safety and reliability of DNNs in critical applications.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in AI safety and formal verification. It significantly advances the state-of-the-art in relational verification of neural networks by introducing a novel Branch-and-Bound approach. This work directly addresses the limitations of existing methods, particularly in handling complex, real-world scenarios involving dependencies across multiple network executions. The novel approach improves precision, paving the way for more reliable and trustworthy AI systems. The efficient algorithms and strong experimental results demonstrate the practical applicability of the method, opening avenues for future research in robust and safe AI development.
Visual Insights#

This figure shows the comparison of the worst-case k-UAP accuracy over time for three different CIFAR-10 ConvSmall DNNs trained with different robust training methods (DiffAI, SABR, CITRUS). The x-axis represents time in seconds, and the y-axis represents the worst-case k-UAP accuracy (averaged over 10 runs). The figure demonstrates that RABBit consistently outperforms the α, β-CROWN baseline across all DNNs and time intervals, highlighting RABBit’s improved precision in k-UAP verification.

This table presents a comparison of RABBit’s performance against several state-of-the-art baselines for worst-case universal adversarial perturbation (UAP) accuracy. It shows the results across different datasets (CIFAR-10 and MNIST), network architectures (ConvSmall and ConvBig), training methods (standard, DiffAI, SABR, CITRUS), and perturbation bounds (epsilon). For each configuration, the table lists the worst-case UAP accuracy achieved by each method, including the improvement achieved by RABBit’s strong bounding and strong branching algorithms, along with RABBit’s overall performance. The results highlight RABBit’s superior precision in relational verification compared to existing methods.
In-depth insights#
Relational Verification#
Relational verification in the context of deep neural networks (DNNs) tackles the challenge of verifying properties that depend on the relationships between multiple DNN executions, rather than individual executions. Existing methods often fall short due to the computational complexity of reasoning across multiple executions. This limitation leads to imprecise results, especially concerning properties like robustness against universal adversarial perturbations (UAPs). A novel branch-and-bound (BaB) approach, potentially leveraging mixed integer linear programming (MILP), is needed to efficiently manage this complexity. This approach may involve intelligently combining branching strategies that explore multiple execution paths with cross-executional bound refinement techniques, effectively reducing the search space. The challenge lies in designing algorithms that are both precise and scalable, capable of handling the exponential growth in the problem size as the number of executions increases. Key to success is exploiting the dependencies between executions to obtain tighter bounds and improve the verification accuracy. Finally, it is crucial to consider the practical limitations of any such approach, particularly regarding the scalability to larger DNNs and datasets.
Branch-and-Bound#
Branch-and-bound (BnB) is a core algorithmic strategy in the paper, significantly enhancing the precision of relational DNN verification. The approach cleverly combines branching strategies over multiple DNN executions with cross-executional bounding, addressing limitations of prior methods which either lacked branching or effective utilization of relational constraints. Two distinct BnB algorithms are presented: ‘strong bounding,’ applying cross-execution bounding at each step for tighter bounds, and ‘strong branching,’ independently branching over executions using pre-computed approximations. The innovative fusion of these two approaches via MILP optimization is a key contribution, providing the best performance. This strategy tackles the computational complexity of exact DNN verification by breaking down the problem into smaller, more manageable subproblems, iteratively refining bounds to converge towards a solution. The effectiveness is demonstrated empirically across various datasets and network architectures. The core innovation lies in efficiently combining branching with the use of cross-execution relationships, overcoming the computational hurdles of the problem, thus advancing the state-of-the-art in relational DNN verification.
Cross-execution#
The concept of “Cross-execution” in the context of verifying relational properties of Deep Neural Networks (DNNs) centers on leveraging dependencies between multiple executions of the same DNN. Instead of treating each execution in isolation, this approach recognizes that the outputs of multiple DNN executions, when subject to related inputs (e.g., those perturbed by a universal adversarial perturbation), are interconnected. This interconnectedness enables more precise verification because relational constraints can be applied across executions, significantly improving the accuracy of the bounds. A key challenge is efficiently managing the computational cost associated with analyzing multiple executions simultaneously. The paper explores branching strategies and cross-executional bound refinement techniques to address this scalability issue while maintaining precision, showing that combining these methods yields substantial gains over state-of-the-art baselines. The effectiveness of cross-execution techniques highlights the need to move beyond individual-execution analysis when dealing with relational properties in DNN verification, where understanding how different inputs affect the network’s behavior collectively is critical.
MILP Optimization#
Mixed Integer Linear Programming (MILP) is a crucial technique in the formal verification of neural networks. Its ability to precisely model piecewise linear activation functions, such as ReLU, makes it theoretically ideal for rigorous verification. However, the computational cost of MILP optimization scales exponentially with the number of integer variables, posing a significant scalability challenge. This is particularly problematic when verifying relational properties requiring analysis of multiple network executions, as the number of variables explodes. The paper explores strategies to mitigate this complexity by combining branching techniques with cross-execution bound refinements. These strategies aim to reduce the number of integer variables while maintaining a high level of precision, improving upon the limitations of existing methods which either lack branching or do not fully leverage relational constraints. This efficient integration of MILP with other techniques is key to making relational verification practical. The authors demonstrate this through extensive experimentation, showcasing RABBit’s effectiveness against existing state-of-the-art methods. While MILP remains computationally intensive, the novel approach significantly reduces its limitations, enabling more precise and scalable relational verification of neural networks.
UAP Robustness#
Universal adversarial perturbations (UAPs) pose a significant challenge to the robustness of deep neural networks (DNNs). A UAP is a carefully crafted perturbation that can fool a DNN across a wide range of inputs, significantly impacting the model’s reliability, especially in safety-critical applications. Effective defense against UAPs is crucial for ensuring the trustworthiness and security of DNNs. This requires verification methods that go beyond traditional input-specific robustness analysis and consider the relationships between multiple DNN executions under the influence of a common perturbation. Current research emphasizes the need for relational verification techniques that can efficiently and precisely reason about these dependencies, moving beyond methods that treat each execution independently. This involves clever bounding techniques that can leverage constraints across multiple executions. Scalability remains a key challenge, as the computational cost of relational verification can increase exponentially with the number of inputs and the complexity of the DNN. Therefore, efficient algorithms, such as branch-and-bound methods, are needed to address the scalability and precision limitations of existing relational verification techniques. Future research will likely focus on developing more sophisticated and scalable verification methods that can provide stronger guarantees of UAP robustness for DNNs used in various real-world applications.
More visual insights#
More on figures

This figure shows the timewise comparison of worst-case k-UAP accuracy between RABBIT and α-β-CROWN for three different CIFAR10 ConvSmall DNNs trained with different robust training methods (DiffAI, SABR, CITRUS). The x-axis represents the time in seconds, and the y-axis represents the k-UAP accuracy (averaged over 10 runs). The results demonstrate that RABBIT consistently outperforms α-β-CROWN across all DNNs and time intervals. This highlights RABBIT’s efficiency and precision improvements in relational verification.
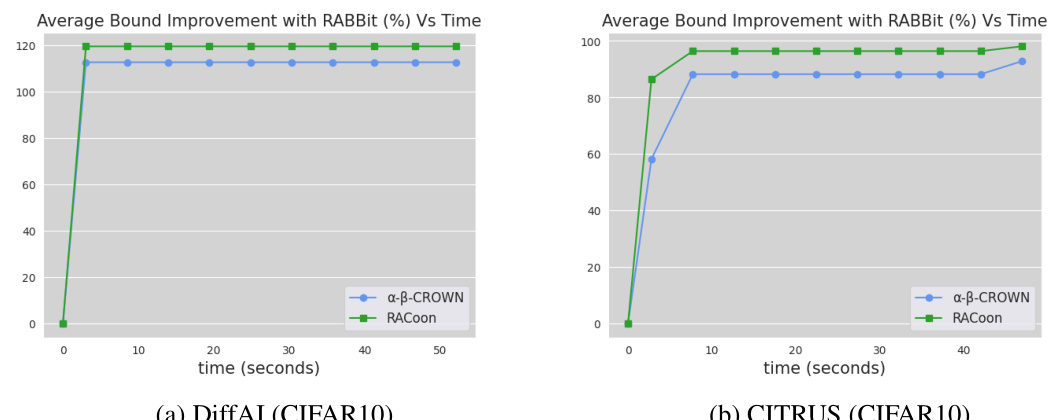
This figure displays the average percentage improvement in t* achieved by strong bounding in RABBit over α,β-CROWN and RACoon across different time intervals, for both DiffAI and CITRUS ConvSmall networks on CIFAR10 dataset. The results highlight how strong bounding’s advantage increases over time, emphasizing its efficiency and precision improvement for relational verification.
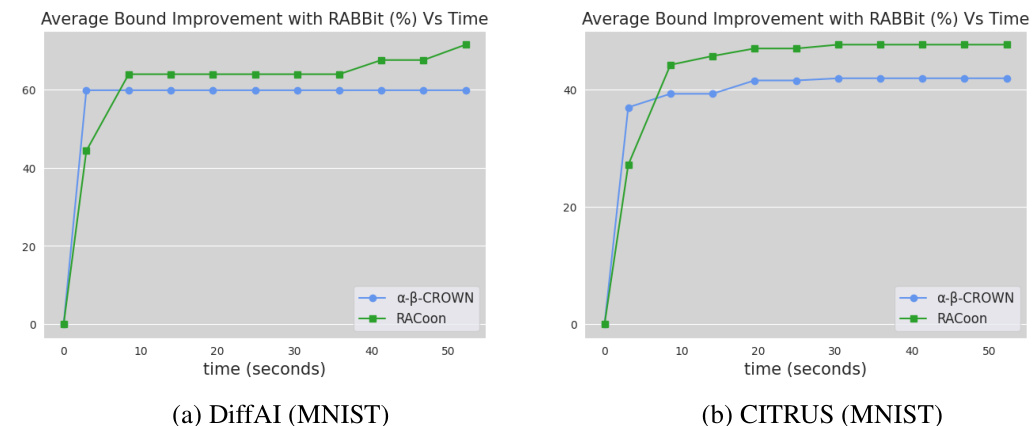
This figure shows the timewise analysis of the average percentage improvement in t* achieved by strong bounding over α, β-CROWN and RACoon for CIFAR10 datasets. The plots illustrate the improvement over time for two different training methods, DiffAI and CITRUS. It demonstrates that the strong bounding method consistently yields tighter bounds than the baselines across various time frames.

This figure compares the worst-case k-UAP accuracy of three different verifiers (RACoon, α-β-CROWN, and RABBit) against varying epsilon values for two different CIFAR10 DNNs trained with DiffAI and CITRUS methods. It showcases the performance of each verifier in terms of accuracy against universal adversarial perturbations (UAPs) with different magnitudes (epsilon values). The graphs illustrate how the accuracy of each verifier changes as the allowed perturbation size (epsilon) increases. It shows RABBit consistently outperforms the other two verifiers.
More on tables

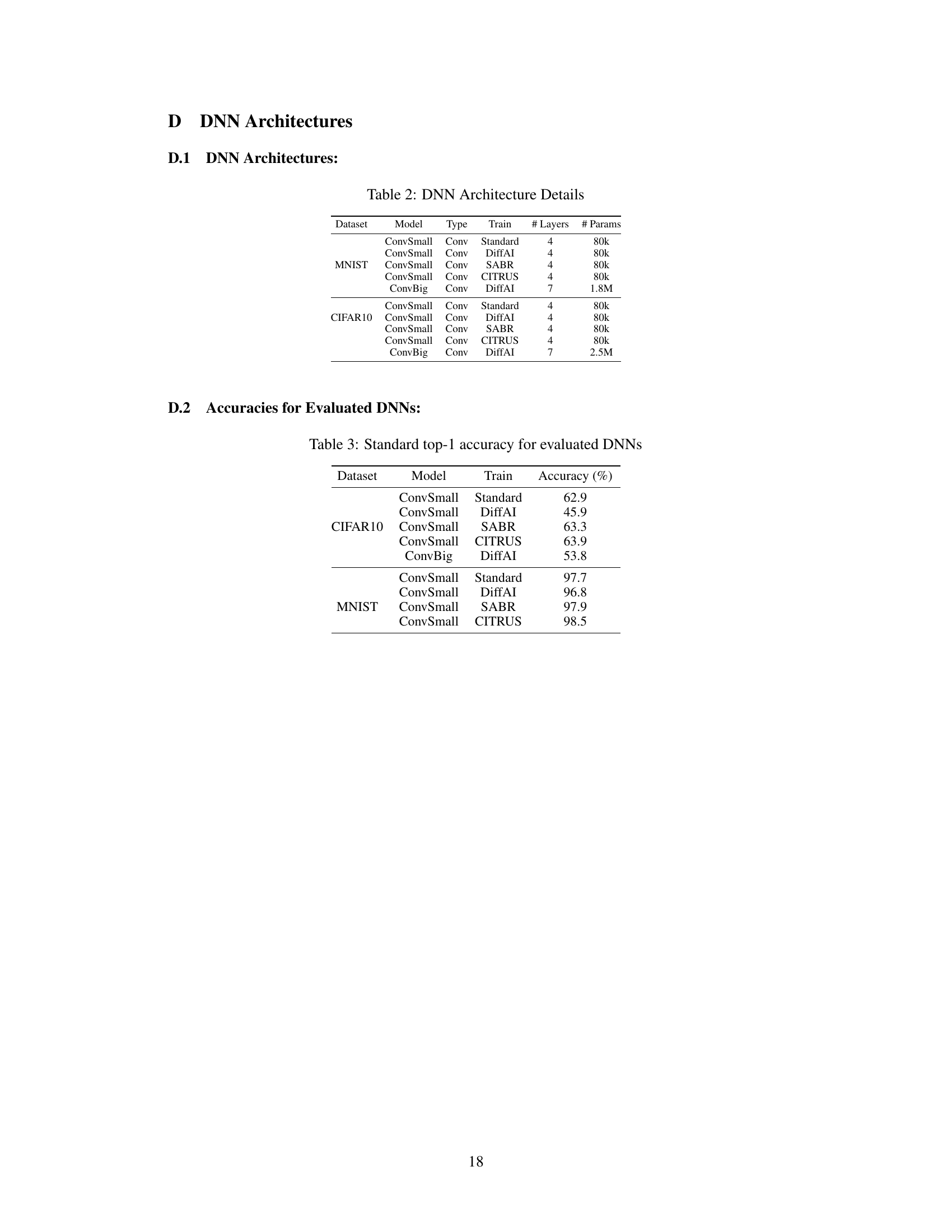
This table presents details about the architectures of the deep neural networks (DNNs) used in the experiments. It lists the dataset, model name, model type (convolutional), training method used to create the model (Standard, DiffAI, SABR, CITRUS), the number of layers in the network architecture, and the total number of parameters in the model. The table covers both MNIST and CIFAR10 datasets using various models, each having been trained using different training methods.
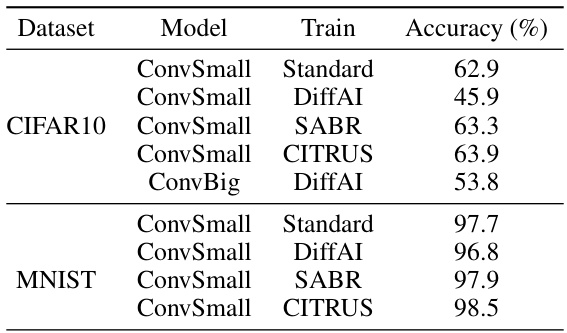
This table presents the standard top-1 accuracy for the evaluated deep neural networks (DNNs). The accuracy is reported for different datasets (CIFAR10 and MNIST) and DNN models (ConvSmall and ConvBig), each trained with various methods (Standard, DiffAI, SABR, and CITRUS). These values represent the baseline performance of each DNN before relational verification.

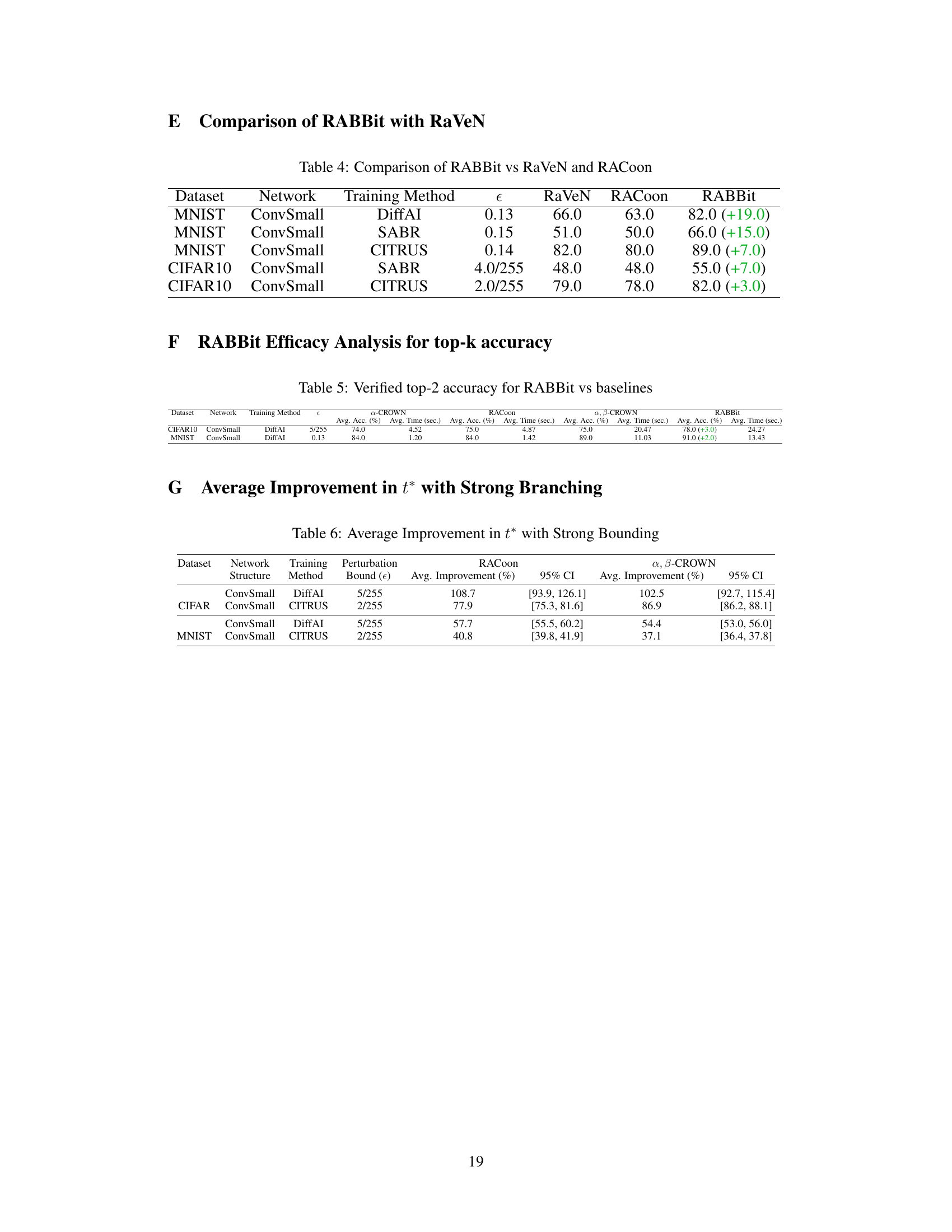
This table compares the performance of RABBit against RaVeN and RACoon on various datasets and network architectures trained with different methods. It shows the worst-case UAP accuracy achieved by each method for each experimental setup, highlighting the improvement achieved by RABBit over RaVeN and RACoon. The values in parentheses indicate the percentage improvement of RABBit over the corresponding baseline method.

This table presents the average percentage improvement achieved by the strong bounding method in the objective function t* compared to two state-of-the-art baselines (RACoon and α, β-CROWN). The results are shown for different datasets (CIFAR and MNIST), network architectures (ConvSmall), training methods (DiffAI and CITRUS), and perturbation bounds (ε). 95% confidence intervals are provided to indicate the statistical significance of the improvements.
Full paper#