Universal Neural Functionals

↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working with neural networks and optimizers because it presents a novel method for creating permutation-equivariant models that are applicable to diverse network architectures, leading to improved optimization and generalization. It opens new avenues for creating more expressive and efficient learned optimizers, which is a significant trend in the field. The open-sourced codebase further enhances its impact on the research community.

Visual Insights

#

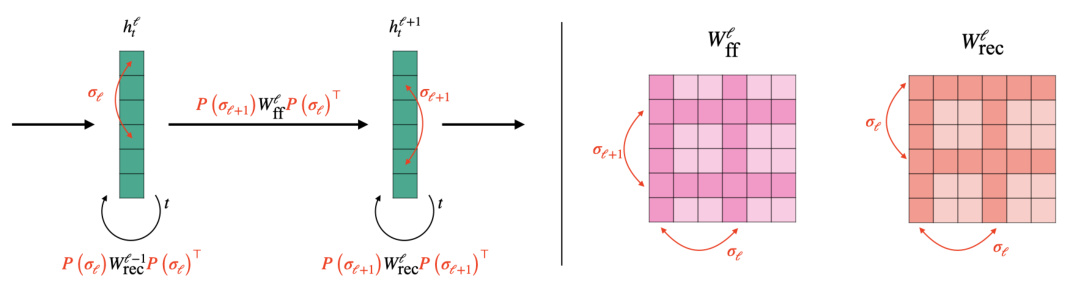
This figure illustrates how permutation symmetries affect the weights of a recurrent neural network. The left side shows how permuting the hidden activations (h^ℓ) doesn’t change the final output (h^f), while the right side shows how this permutation affects both feedforward and recurrent weights (W^ff and W^rec) by permuting their rows and columns accordingly. This example demonstrates the type of weight space permutation symmetries the paper’s algorithm handles.

This table presents the results of an experiment comparing the performance of three different methods in predicting the success rate of Recurrent Neural Networks (RNNs) trained for an arithmetic task. The methods are Deep Sets, STATNN (a strong baseline method), and the proposed Universal Neural Functional (UNF) method. The evaluation metric is Kendall’s tau (τ), which measures rank correlation. The results demonstrate that UNF significantly outperforms the other two methods.

In-depth insights

#

Equivariant Layers

#

The concept of “Equivariant Layers” in the context of neural networks is crucial for building models that respect inherent symmetries within the data. Equivariance ensures that if the input data undergoes a transformation (like rotation or permutation), the output of the layer undergoes a corresponding transformation. This property is highly desirable because it allows the model to learn more effectively from data with inherent structures. The paper likely explores different techniques for constructing such layers. For example, it might focus on weight-sharing schemes, where specific sets of weights are reused across different parts of the network to maintain symmetry. Alternatively, it could explore the use of specific activation functions or layer architectures that inherently possess the equivariance property. The effectiveness of equivariant layers is especially noticeable when handling data with permutation symmetries, such as when processing sets of data points where the order does not matter. Building deep models using equivariant layers involves composing these layers while ensuring their equivariance properties are preserved. The choice of architecture and design heavily influences model performance and generalization.

Learned Optimizers

#

The section on “Learned Optimizers” explores the use of neural networks to design optimizers, moving beyond traditional methods like SGD. This meta-learning approach trains a neural network (the optimizer) to learn how to best update model parameters given a specific architecture and task. The authors highlight the benefits of incorporating permutation equivariance into the design of these learned optimizers by leveraging Universal Neural Functionals (UNFs). UNFs offer increased flexibility and expressiveness compared to previous methods, handling various network architectures (MLPs, CNNs, RNNs, Transformers) that would otherwise require task-specific designs. The experiments showcase the superior performance of UNFs based optimizers against standard optimizers and other meta-learned optimizers that lack permutation equivariance, achieving lower training loss and faster convergence across diverse tasks. The results provide strong evidence for the advantages of leveraging symmetry properties within the weight space when designing efficient and effective learned optimizers. This work is a significant contribution to the field of meta-learning, pushing the boundaries of learned optimizers and offering a powerful and versatile tool for training complex models.

RNN Generalization

#

The section on RNN generalization likely explores the use of neural functionals, specifically universal neural functionals (UNFs), to predict the generalization performance of recurrent neural networks (RNNs) from their weights. This is a significant area of research because understanding and predicting how well an RNN will generalize to unseen data is crucial for effective model selection and training. The authors may present a novel method using UNFs, outperforming existing methods like STATNN in predicting RNN test success rates on an arithmetic task. This success highlights the potential of UNFs to capture nuanced information within the RNN weight space that is otherwise missed by traditional methods. A key aspect is likely the invariance property of the UNFs ensuring that the model’s prediction remains consistent under neuron permutations of the weights, a desirable characteristic given the inherent symmetry in RNN architectures. Furthermore, the results could demonstrate the utility of UNFs for handling the complex weight spaces of RNNs, something that simpler permutation-equivariant models might struggle with. The analysis likely also involves comparing UNFs with other weight-space analysis techniques, such as Deep Sets and NFNs. The findings would likely support the claim that UNFs are more suitable for learning from and using the structural properties of complicated weight spaces, leading to improved generalization prediction accuracy and a deeper understanding of RNN behavior.

Weight Space Maps

#

The concept of “Weight Space Maps” in the context of neural networks represents a powerful abstraction for analyzing and manipulating the learned parameters (weights and biases) of a model. It moves beyond simply viewing weights as individual scalars to consider them as a collective entity, residing in a high-dimensional space. This allows for the exploration of geometric properties and relationships within the weight space, which can reveal crucial insights into model behavior, generalization, and optimization. Understanding how weights cluster, form manifolds, or exhibit specific symmetries can offer a deep understanding of model capacity, implicit biases, and the optimization landscape. The study of weight space maps is particularly useful for creating permutation-equivariant models. These models explicitly leverage the intrinsic symmetries of weight spaces, which can lead to more efficient and robust training and improved generalization. This is especially relevant for complex architectures where simple permutation symmetries of basic feedforward networks may not hold. Weight space maps provide a fundamental framework for developing new methods for model analysis, design, and optimization, moving beyond the limitations of traditional approaches and paving the way for more sophisticated and effective deep learning techniques.

Future Directions

#

The paper’s core contribution is a novel method for constructing permutation-equivariant neural functionals applicable to arbitrary weight spaces, marking a significant advancement beyond previous methods limited to simple MLPs and CNNs. Future research directions could focus on extending UNFs to handle heterogeneous weight-space inputs, allowing a single UNF to act as a learned optimizer for diverse architectures. This necessitates addressing the computational complexity that arises with more complex networks. Another crucial area for future work involves thorough testing of generalization capabilities across a much wider array of tasks and datasets, going beyond the small-scale experiments presented. Investigating the scalability challenges of UNFs, particularly for higher-rank tensors and higher-order interactions, is essential. This involves exploring more efficient meta-gradient estimators capable of handling high-dimensional spaces. Finally, a comprehensive analysis of the trade-offs between UNF expressiveness and computational cost relative to alternative methods such as MPNNs is vital to establish its practical utility in large-scale applications.

More visual insights

#

More on tables

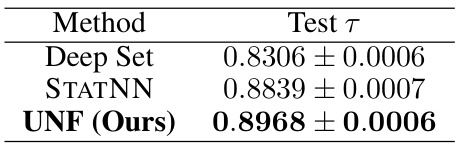
This table shows the results of an experiment comparing three different methods for predicting the success rate of recurrent neural networks (RNNs) trained on an arithmetic task. The methods are Deep Sets, STATNN (a strong baseline), and UNF (the proposed method). The performance is measured using Kendall’s Tau (τ), which is a rank correlation coefficient. The table shows that UNF significantly outperforms both Deep Sets and STATNN, indicating that it’s more effective at extracting information from the RNN weights to predict their performance.

This table presents the number of parameters used by the function f(·) in different learned optimizers (UNF, Deep Set, NFN) across various tasks (MLP on FashionMNIST, CNN on CIFAR-10, RNN on LM1B, Transformer on LM1B). Note that the parameter count excludes meta-learned scalars α, γ, and β. The UNF and NFN optimizers are equivalent in the MLP task.

Full paper

#