↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Training energy-based models (EBMs) on discrete or mixed data is challenging due to the difficulty of sampling from the unnormalized probability distribution. Existing methods often rely on Markov Chain Monte Carlo (MCMC), which can be computationally expensive and lack theoretical guarantees. This paper addresses these challenges by introducing a novel loss function called Energy Discrepancy (ED) and proposing a framework to efficiently train discrete EBMs.
The proposed framework uses discrete diffusion processes on structured spaces, informed by the data’s underlying graph structure. The continuous-time parameter of the diffusion process provides fine-grained control over the perturbation, improving the quality of the model’s learning. The authors demonstrate the method’s effectiveness on several datasets, showing improved performance over existing MCMC-based approaches in various downstream tasks, including synthetic data generation and classification.
Key Takeaways#
Why does it matter?#
This paper is crucial because it introduces a novel training method for energy-based models (EBMs) that overcomes the limitations of existing methods for handling discrete and mixed data. This opens doors for more accurate and efficient probabilistic modeling in various domains, like tabular data analysis and image generation, significantly advancing machine learning research.
Visual Insights#

This figure illustrates different types of state spaces that can be represented in a tabular dataset. It shows how numerical variables (represented by a continuous space Rd), cyclical categorical variables (like seasons), ordinal categorical variables (like age), and unstructured categorical variables can all be included in a single dataset. The figure also shows how an ‘absorbing state’ can be used to indicate a missing or masked value. The different graph structures illustrate how various dependencies among variables can be represented.
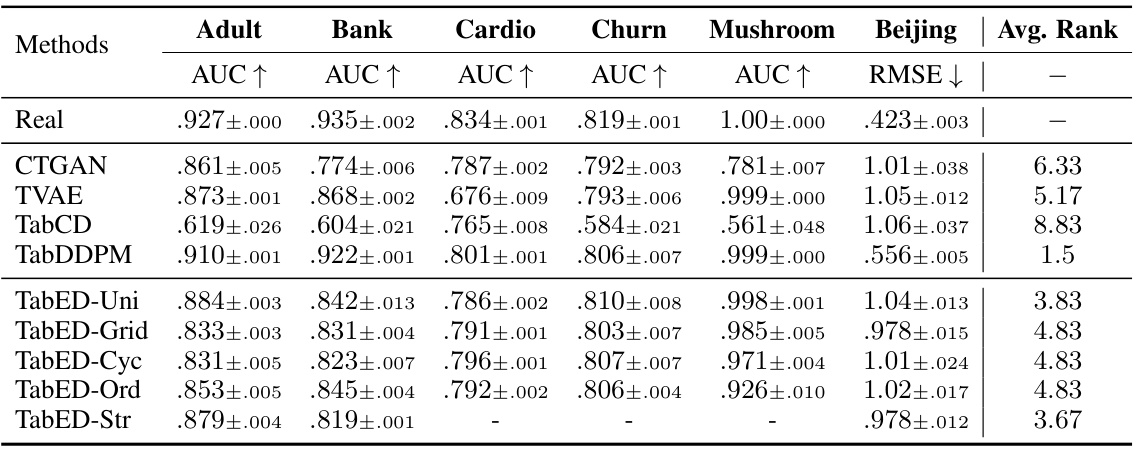
This table presents the results of experiments conducted on six real-world tabular datasets using various methods for tabular data synthesis. The methods compared include CTGAN, TVAE, TabCD, TabDDPM, and several variants of the proposed TabED method (TabED-Uni, TabED-Grid, TabED-Cyc, TabED-Ord, TabED-Str). The evaluation metrics used are AUC (Area Under the ROC Curve) for classification tasks and RMSE (Root Mean Squared Error) for the regression task. The average rank across all datasets is also provided, indicating the overall performance of each method.
In-depth insights#
Discrete EBM Training#
Training Energy-Based Models (EBMs) on discrete data presents unique challenges due to the intractability of normalization and the difficulty in sampling from the unnormalized probability distribution. Traditional methods like contrastive divergence (CD) rely on Markov Chain Monte Carlo (MCMC) sampling, which can be slow, computationally expensive, and lack theoretical guarantees. Energy Discrepancy (ED) offers a promising alternative by formulating a loss function that avoids explicit sampling, relying instead on the evaluation of the energy function at data points and their perturbed counterparts. This approach is particularly attractive for discrete data because it bypasses the need for complex sampling schemes tailored to discrete spaces, which can be challenging to design and implement efficiently. The effectiveness of ED for discrete EBM training is further enhanced by the introduction of discrete diffusion processes, enabling data perturbation methods informed by the inherent structure of the discrete space, leading to better gradient estimates and improved training stability. The choice of perturbation process, whether based on uniform, cyclical, or ordinal structures, is crucial and can significantly impact the effectiveness of training. Overall, ED offers a powerful and efficient framework for discrete EBM training, overcoming some of the limitations associated with traditional methods.
Heat Equation Diffusion#
The concept of ‘Heat Equation Diffusion’ in the context of energy-based models for discrete data offers a novel approach to generating perturbations for training. Instead of relying on computationally expensive Markov Chain Monte Carlo (MCMC) methods, this technique leverages the heat equation to simulate a diffusion process directly on the discrete state space. This is particularly useful for structured discrete data (like graphs or images) where the graph structure itself can inform the diffusion process, making the perturbation more meaningful and data-efficient. The continuous-time parameter in the heat equation provides fine-grained control over the perturbation strength. This allows for a trade-off between exploration and exploitation in the training process, potentially improving convergence speed and sample quality. The use of a graph Laplacian to define the rate matrix of the diffusion further enhances the approach’s suitability for structured data. The theoretical analysis of the heat equation’s convergence to maximum likelihood estimation and its Gaussian limiting behavior provides strong support for the method’s soundness. The efficacy of this approach hinges on the choice of perturbation and its alignment with the data’s intrinsic structure. This technique might be particularly beneficial for high-dimensional discrete data, where traditional MCMC methods struggle.
Energy Discrepancy Loss#
The concept of “Energy Discrepancy Loss” presents a novel approach to training energy-based models (EBMs), particularly advantageous when dealing with discrete or mixed data. It bypasses the computationally expensive Markov Chain Monte Carlo (MCMC) sampling techniques typically required for estimating the gradient of the log-likelihood in EBMs. Instead, it leverages the energy function evaluations at data points and their perturbed counterparts. The efficacy of this method hinges on the design of the perturbation mechanism, which, as shown in the paper, can effectively incorporate structural information from the data space (e.g., using graph Laplacians for discrete data) to create informative perturbations. The theoretical analysis demonstrates convergence towards maximum likelihood estimation under specific conditions, making it a principled and robust alternative to traditional contrastive divergence methods. However, the success and performance also depend on the choice of perturbation and its scale, requiring careful consideration and potential tuning for optimal results. Practical applications shown in the paper highlight the power of this approach in tasks ranging from density estimation and synthetic data generation to tabular data analysis, demonstrating its potential impact in various domains.
Tabular Data Synthesis#
The synthesis of tabular data, a complex data type combining numerical and categorical features, presents a significant challenge for probabilistic modeling. Existing methods often struggle with this data modality. Energy-based models (EBMs), while flexible, traditionally face difficulties due to the intractability of normalization and the need for robust sampling methods. This research addresses these challenges by extending the energy discrepancy loss function, offering a robust training method for EBMs on tabular data that eliminates the need for Markov Chain Monte Carlo (MCMC). The approach cleverly leverages discrete diffusion processes on structured spaces to inform the selection of perturbations, a crucial aspect of the energy discrepancy method. Experiments on both synthetic and real-world datasets demonstrate promising results in tabular data generation, showcasing the efficacy and robustness of the proposed method. The ability to handle mixed-data types seamlessly is highlighted as a key advancement, opening the door for broader applications in data augmentation and other downstream tasks.
Future Work: Scalability#
Future work on scalability for energy-based models (EBMs) trained with energy discrepancy should prioritize addressing limitations in handling high-dimensional and complex data structures. Improving sampling efficiency for discrete spaces, perhaps by leveraging advancements in discrete diffusion models or developing novel sampling strategies tailored to the specific graph structure of the data, is crucial. Research into more efficient approximation techniques for the contrastive potential could also significantly improve scalability. Exploring alternative loss functions or training methods that avoid explicit sampling altogether might offer further avenues for optimization. Additionally, parallelization strategies need development to fully harness the potential of the energy discrepancy framework for large-scale applications. Finally, investigation into the theoretical guarantees of the method under various data distributions and dimensions is needed to provide insights for practical scalability and applicability.
More visual insights#
More on figures
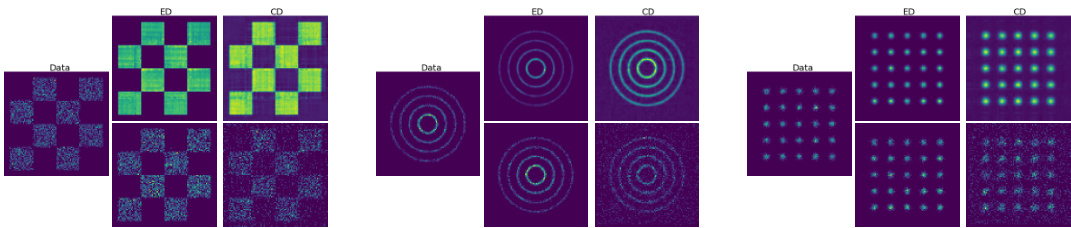
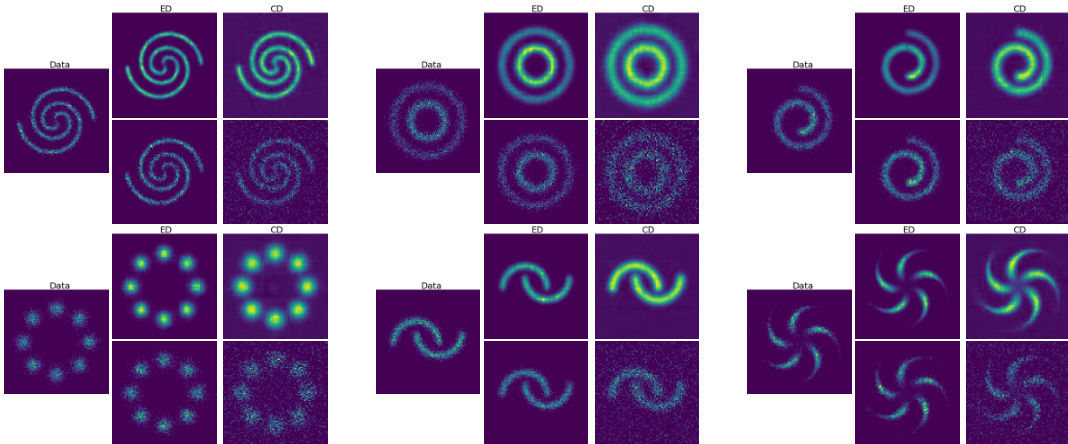
This figure compares the performance of energy discrepancy (ED) and contrastive divergence (CD) in estimating a probability distribution with 16 dimensions and 5 states. The top row shows the true data distribution (Data), the ED estimated density, and the CD estimated density. The bottom row displays samples generated from the ED and CD models, respectively. The figure visually demonstrates that energy discrepancy produces a more accurate estimate of the density and generates samples that better reflect the true distribution’s characteristics.

This figure shows a comparison of samples generated using contrastive divergence (CD) and energy discrepancy (ED) methods on a synthetic tabular dataset. The leftmost panel shows the original data distribution, which exhibits a clear ring structure with distinct color clusters within each ring. The middle panel shows samples generated using contrastive divergence. These samples are dispersed more randomly, indicating that the CD method is not capturing the underlying structure of the data as effectively. The rightmost panel shows samples generated using energy discrepancy. These samples are more concentrated around the ring structure and maintain the color clustering more accurately, showing that the ED method successfully captures the data’s underlying structure. This visual comparison illustrates the superior performance of energy discrepancy in generating realistic samples from complex data distributions.
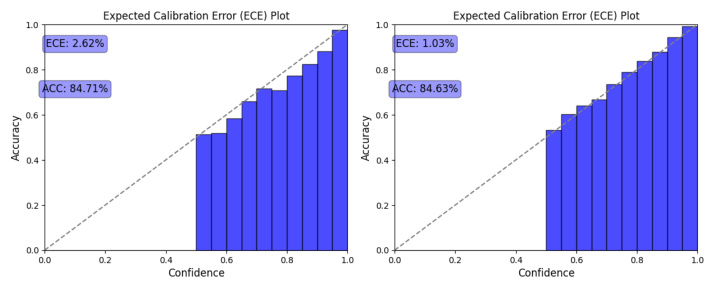
This figure compares the calibration results of two classification models: a baseline model (left) and a model trained using energy discrepancy (right), both applied to the ‘adult’ dataset. The Expected Calibration Error (ECE) plots show that the model trained with energy discrepancy exhibits better calibration than the baseline model, evidenced by a lower ECE (2.62% vs. 1.03%). This suggests that the energy discrepancy method produces more reliable confidence scores in its predictions.

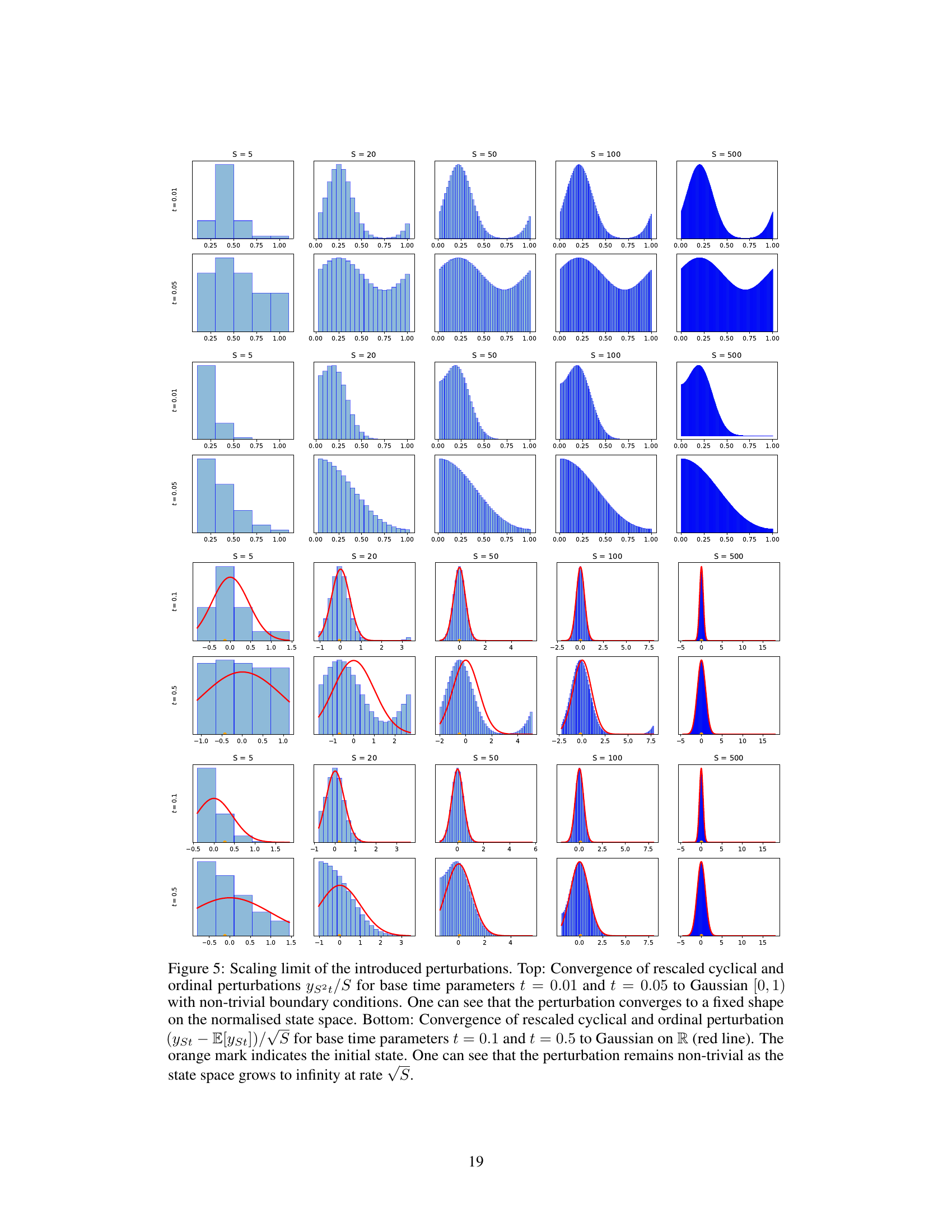
This figure shows the convergence of cyclical and ordinal perturbations to a Gaussian distribution as the state space size increases. The top row shows the convergence of the rescaled perturbations to a fixed shape on the normalized state space for different base time parameters. The bottom row shows the convergence of the rescaled and centered perturbations to a Gaussian distribution on R.
This figure compares the performance of energy discrepancy (ED) and contrastive divergence (CD) in estimating the probability density and generating samples from a dataset with 16 dimensions and 5 states. The top row shows the true data distribution and then the estimated density functions produced by ED and CD methods. The bottom row displays samples generated by each method, illustrating the differences in their ability to capture the multi-modal nature of the distribution.

This figure compares the performance of energy discrepancy (ED) and contrastive divergence (CD) in estimating probability distributions on a dataset with 16 dimensions and 5 states. The top row shows the true data distribution and the ED and CD estimated densities. The bottom row shows samples generated from the learned models using ED and CD. The figure visually demonstrates that ED produces a more accurate density estimation and generates samples that more closely resemble the true data distribution compared to CD.
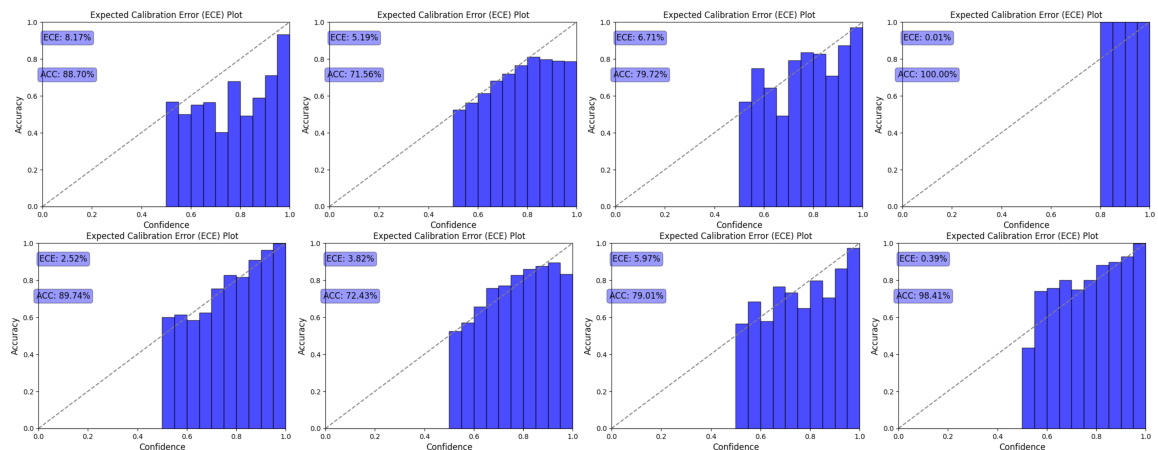
This figure compares the performance of energy discrepancy and contrastive divergence methods for estimating probability density and generating synthetic samples from a dataset with 16 dimensions and 5 states. The top row displays the estimated probability density functions obtained by using the two different methods. The bottom row shows samples synthesized using the same methods. It showcases how the energy discrepancy method produces more accurate density estimations and better-quality synthetic samples compared to the contrastive divergence method.

This figure compares the performance of energy discrepancy (ED) and contrastive divergence (CD) in estimating the probability distribution of a dataset with 16 dimensions and 5 states for each dimension. The top row displays the estimated probability density learned by each method. The bottom row presents samples generated from the learned models. Visually, energy discrepancy produces a sharper, more accurate representation of the density, with samples that more closely reflect the true data distribution. Contrastive divergence, in contrast, shows a less refined density estimation and produces samples less aligned with the true data distribution.
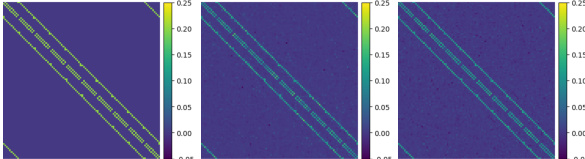
This figure shows the results of an experiment to verify the scaling limit of the cyclical and ordinal perturbations, as described in Theorem 2. The top row shows that as the size of the state space (S) increases, both cyclical and ordinal perturbations converge to a Gaussian distribution on the interval [0,1), which is consistent with Theorem 2. The bottom row demonstrates that rescaling the perturbation by √S results in convergence to a Gaussian distribution on the real numbers.
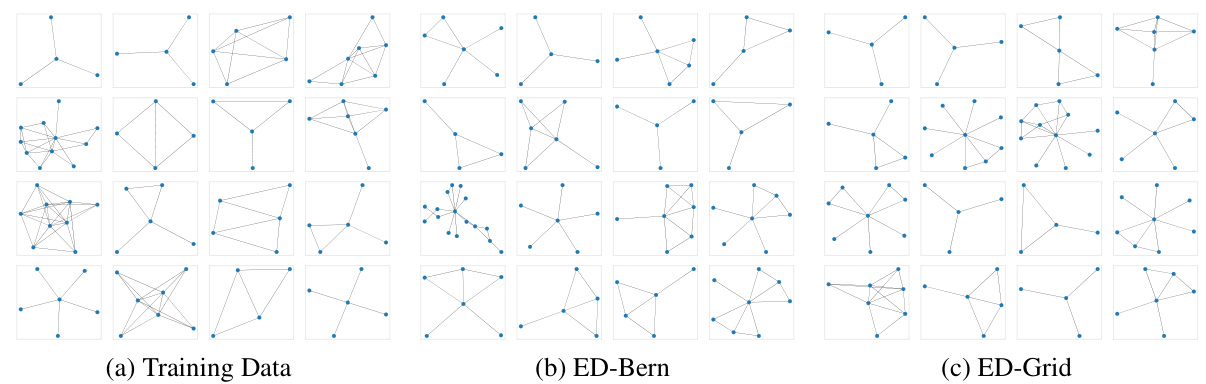
This figure visualizes the results of graph generation using different methods. Subfigure (a) shows examples from the Ego-small training dataset. Subfigures (b) and (c) display graphs generated using the ED-Bern and ED-Grid methods, respectively, showcasing the models’ ability to learn and generate realistic graph structures similar to the training data.
More on tables

The table presents the negative log-likelihood (NLL) results for various discrete image modeling methods on three different datasets: Static MNIST, Dynamic MNIST, and Omniglot. It compares the performance of the proposed Energy Discrepancy (ED) methods (ED-Bern and ED-Grid) against existing approaches including Gibbs sampling, Gibbs with Gradients (GWG), Energy-based Generative Flow Networks (EB-GFN), and Discrete Unadjusted Langevin Algorithm (DULA). The results show the effectiveness of ED in achieving comparable or superior NLL performance compared to the baselines.

This table compares the performance of different methods for discrete density estimation. The negative log-likelihood (NLL) is used as the evaluation metric. It shows the results for various synthetic datasets (2spirals, 8gaussians, circles, moons, pinwheel, swissroll, checkerboard), and includes results from several baseline methods (PCD, ALOE+, EB-GFN) for comparison. The table highlights the effectiveness of the proposed method (ED-Bern and ED-Grid) compared to existing approaches.
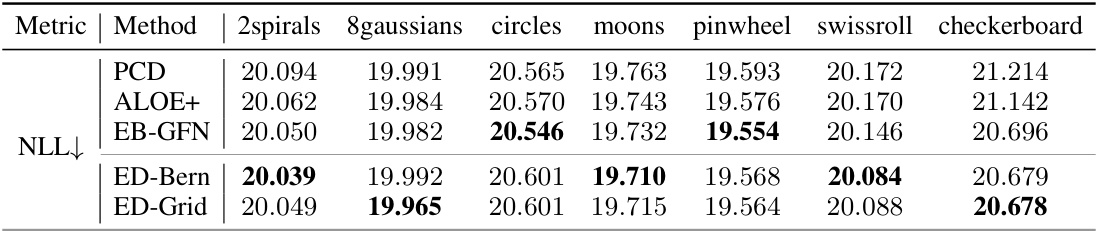
The table presents the negative log-likelihood (NLL) results for discrete density estimation using different methods. It compares the performance of the proposed Energy Discrepancy (ED) approach (ED-Bern and ED-Grid) against three baseline methods: PCD, ALOE+, and EB-GFN. The results are shown for eight different synthetic datasets, each with unique characteristics.
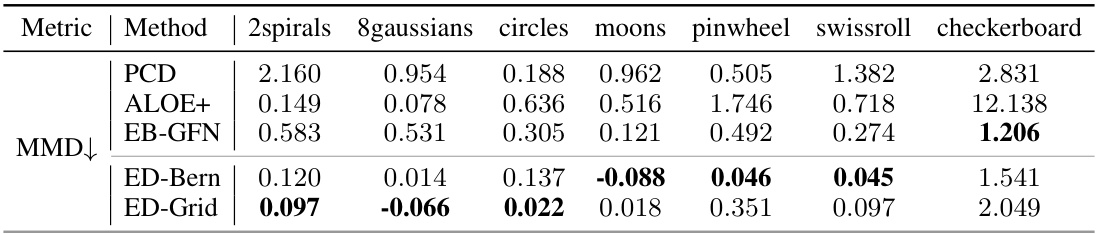
This table presents the Maximum Mean Discrepancy (MMD) results for different discrete density estimation methods on several synthetic datasets. Lower MMD values indicate better performance, reflecting a closer match between the estimated density and the true data generating distribution. The results are compared against baselines from a previous study by Zhang et al. (2022a). The datasets include 2spirals, 8gaussians, circles, moons, pinwheel, swissroll, and checkerboard, representing various data distributions.

This table presents the statistics of six real-world datasets used in the paper’s experiments on tabular data synthesis. For each dataset, it shows the number of rows, the number of numerical features (# Num), the number of categorical features (# Cat), and the number of instances in the training, validation, and testing sets. It also specifies the type of task (binary classification or regression) for each dataset. This information is crucial for understanding the experimental setup and the generalizability of the results.
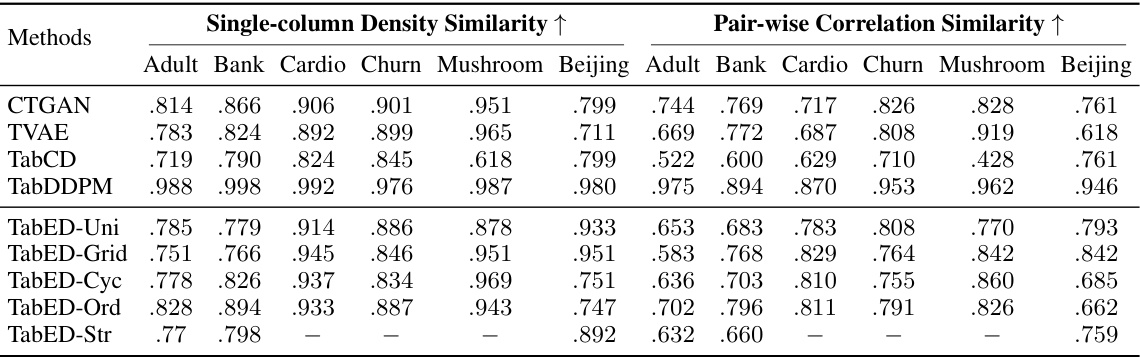
This table presents the results of evaluating the quality of synthetic tabular data generated by various models. Two metrics are used for evaluation: single-column density similarity and pair-wise correlation similarity. Single-column density similarity measures how similar the distribution of values in each individual column is between the real and synthetic data. Pair-wise correlation similarity compares the correlation between pairs of columns in the real and synthetic data. The table shows the results for several different models, including the proposed energy discrepancy (ED) methods and several baselines.

This table compares the running time complexity per iteration and per epoch for energy discrepancy and contrastive divergence methods. The contrastive divergence methods use varying numbers of Markov Chain Monte Carlo (MCMC) steps (CD-1, CD-5, CD-10), while energy discrepancy uses two variants (ED-Bern, ED-Grid). The results show that energy discrepancy methods are significantly faster, particularly because they don’t rely on computationally expensive MCMC sampling.

This table compares the performance of energy discrepancy and contrastive divergence methods for training EBMs on three image datasets (Static MNIST, Dynamic MNIST, and Omniglot). The contrastive divergence results use varying numbers of MCMC steps (CD-1, CD-3, CD-5, CD-7, CD-10), while energy discrepancy results are shown for Bernoulli and Grid versions (ED-Bern, ED-Grid). The negative log-likelihood (NLL) is used as the evaluation metric. The table shows that ED-Bern and ED-Grid consistently achieve comparable or better results than CD with multiple MCMC steps across all three datasets.

This table presents the negative log-likelihood (NLL) results for the static MNIST dataset using the ED-Grid method with varying numbers of negative samples (M). It shows that the model performance is relatively stable across different values of M, indicating robustness to this hyperparameter.

This table compares the performance of different methods for learning the connectivity matrix J in an Ising model with different grid sizes (D) and coupling strengths (σ). The negative log-RMSE metric measures the difference between the learned matrix and the true matrix. Lower values indicate better performance. The table includes results for Gibbs sampling, GWG (Gibbs with gradients), EB-GFN (energy-based generative flow networks), ED-Bern (energy discrepancy with Bernoulli perturbation), and ED-Grid (energy discrepancy with grid perturbation). The results for Gibbs, GWG, and EB-GFN are taken from a previous study by Zhang et al. (2022a).
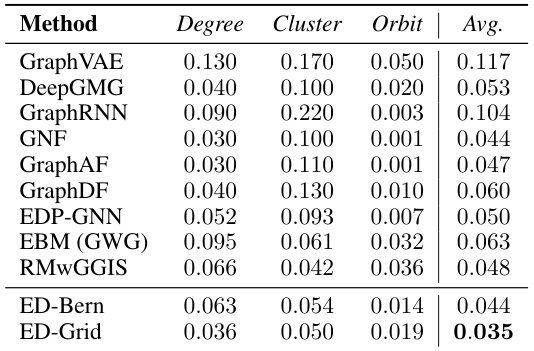
This table presents a comparison of different graph generation methods on the Ego-small dataset. The methods are evaluated based on three graph statistics: degree, cluster, and orbit, using the Maximum Mean Discrepancy (MMD) metric. The ‘Avg.’ column shows the average MMD across these three metrics. Lower MMD values indicate better performance.

This table summarizes the naming conventions and available tuning parameters for all introduced energy discrepancy methods. The structured perturbation TabED-Str uses different perturbations depending on the state space structure: On unstructured data, the uniform perturbation with tuning hyper-parameter tcat is used, while on ordinally and cyclically structured data the ordinal perturbations and cyclical perturbations are used, respectively, with tuning parameter tbase.
Full paper#