↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Top-k classification, predicting the k most likely classes, is valuable but can be inefficient if k is arbitrarily high. Existing methods struggle to balance accuracy and prediction set size. The paper addresses this by introducing the problem of cardinality-aware set prediction, which dynamically adjusts the prediction set’s size based on the input instance.
This new approach uses a target loss function that minimizes classification error while simultaneously controlling the size of the prediction set. To optimize this, the paper introduces two families of surrogate losses: cost-sensitive comp-sum and cost-sensitive constrained losses, with theoretical consistency guarantees. Extensive experiments across multiple datasets demonstrate the effectiveness and benefits of these algorithms, showing significant improvements over traditional top-k classifiers.
Key Takeaways#
Why does it matter?#
This paper is crucial because it introduces a novel approach to top-k classification, a widely used technique in many applications. The cardinality-aware method significantly improves accuracy and efficiency, addressing a key limitation of traditional top-k classifiers. This opens new avenues for research in developing more efficient and accurate algorithms for various machine learning tasks.
Visual Insights#

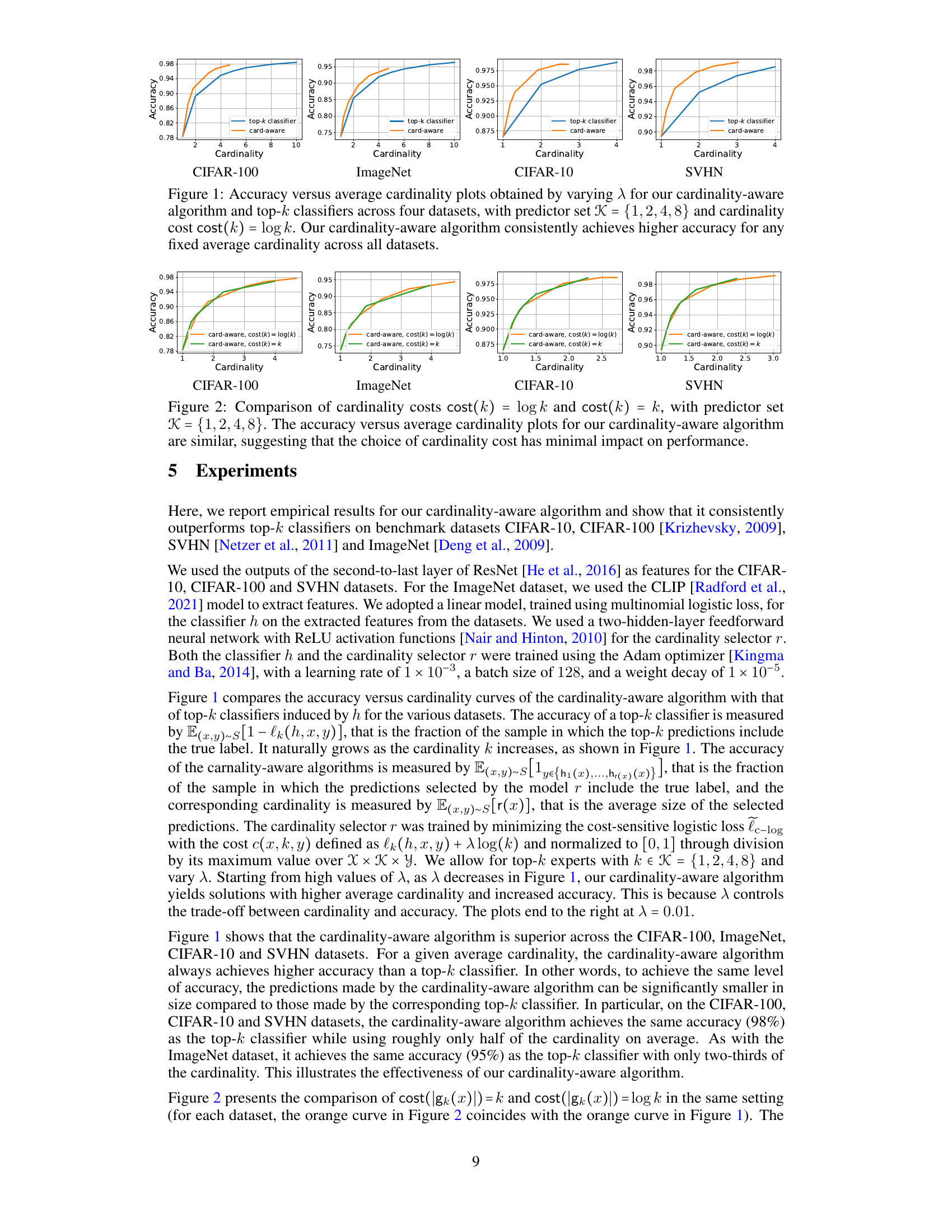
The figure shows the accuracy versus average cardinality for four different datasets (CIFAR-10, CIFAR-100, ImageNet, and SVHN). Two approaches are compared: a standard top-k classifier and a new cardinality-aware algorithm. The cardinality-aware algorithm dynamically adjusts the number of predictions (cardinality) based on input difficulty. The x-axis represents the average cardinality, and the y-axis represents the accuracy. The plots demonstrate that for any given average cardinality, the cardinality-aware algorithm consistently achieves higher accuracy than the top-k classifier, showcasing its effectiveness.
In-depth insights#
Top-k’s Challenges#
Top-k classification, while seemingly a straightforward extension of standard classification, presents unique challenges. The inherent ambiguity in selecting among multiple highly probable classes necessitates robust loss functions that accurately reflect this uncertainty. Unlike binary or multi-class scenarios, traditional loss functions often fail to capture the nuanced nature of top-k prediction. Developing efficient algorithms to minimize these more complex losses becomes computationally expensive. Furthermore, the theoretical analysis of top-k algorithms lags behind that of standard classifiers, making it challenging to provide strong guarantees of consistency and generalization. Another key challenge lies in balancing accuracy and cardinality. Effective top-k systems must dynamically adjust the number of classes predicted based on input difficulty to prevent the inclusion of low-confidence predictions that inflate cardinality. This requires a careful balancing of the accuracy-cardinality trade-off, which might necessitate instance-dependent cost functions and adaptive algorithms.
H-Consistency#
H-consistency, a crucial concept in the study of surrogate loss functions, offers a stronger and more refined guarantee than the traditional notion of Bayes-consistency. Unlike Bayes-consistency, which is an asymptotic property applicable only to the family of all measurable functions, H-consistency provides non-asymptotic and hypothesis-set-specific bounds. This means that H-consistency not only ensures that minimizing a surrogate loss leads to minimizing the true loss asymptotically but also provides quantitative bounds on how close the performance is to the optimal solution for the hypothesis set in use. The value of H-consistency is particularly evident in scenarios involving complex hypothesis sets, where standard guarantees such as Bayes-consistency may fail to provide any meaningful information, but H-consistency still offers valuable non-asymptotic insights. The framework’s rigorous mathematical foundation ensures its reliability and applicability in various machine learning applications, including classification and regression problems. Non-asymptotic bounds ensure that the results are directly applicable to finite samples, unlike Bayes-consistency which offers an asymptotic guarantee only. This means that H-consistency is particularly beneficial in situations with limited data where asymptotic guarantees are less meaningful.
Cost-Sensitive Loss#
Cost-sensitive loss functions are crucial for addressing class imbalance in classification problems. They assign different misclassification costs to different classes, reflecting the real-world impact of errors. For instance, in medical diagnosis, misclassifying a malignant tumor as benign is far more severe than the reverse. Standard loss functions, like cross-entropy, treat all errors equally, which is insufficient when the costs of different errors vary significantly. Cost-sensitive losses modify the learning process to prioritize minimizing more costly errors. This can involve weighting the loss function based on class frequency or assigning weights manually based on domain expertise. The choice of cost-weighting strategy significantly impacts the model’s performance and fairness, necessitating careful consideration of potential biases and implications. Advanced cost-sensitive techniques might incorporate instance-dependent costs to handle nuanced error scenarios, optimizing accuracy while mitigating the negative consequences of specific errors. Empirical evaluation is vital to gauge the effectiveness of a cost-sensitive approach in reducing costly errors, often requiring rigorous analysis of different weighting methods and their impact on model behavior and outcome prediction.
Cardinality Control#
Cardinality control, in the context of machine learning models, particularly those dealing with set prediction and top-k classification, focuses on managing the size of predicted sets. The core idea is to find an optimal balance between accuracy and the number of elements in the output set. A large set might lead to higher accuracy but less efficiency, while a small set may improve efficiency but sacrifice accuracy. Effective cardinality control mechanisms enable models to dynamically adjust set sizes, considering the input’s complexity. This is achieved by introducing carefully designed loss functions that incorporate both classification error and cardinality, such as cost-sensitive comp-sum or cost-sensitive constrained losses. These loss functions allow for instance-dependent cardinality adjustments. Theoretical guarantees, like H-consistency bounds, ensure that algorithms minimizing these loss functions converge to good solutions, providing a strong foundation for cardinality-aware algorithms. Experiments show that cardinality-aware algorithms consistently outperform traditional top-k classifiers, achieving similar accuracy with significantly smaller set sizes, leading to substantial efficiency gains.
Future Research#
The ‘Future Research’ section of this cardinality-aware set prediction paper could explore several promising avenues. Extending the theoretical analysis to broader classes of surrogate loss functions beyond comp-sum and constrained losses would strengthen the framework’s applicability. Investigating the impact of different cost functions on algorithm performance and cardinality control is crucial, particularly for cost functions that better reflect real-world scenarios. Empirical evaluations on more diverse datasets encompassing varied data modalities (text, audio, video) and challenging conditions (noise, class imbalance) could reveal the method’s limitations and generalization abilities. A key area for investigation is developing more efficient algorithms, potentially leveraging advanced optimization techniques or specialized hardware acceleration. Furthermore, exploring the integration of cardinality-aware set prediction with other machine learning tasks like active learning and reinforcement learning would broaden its applicability and address more complex problem settings. Finally, investigating methods for automatically determining the optimal cardinality for a given application without relying on manual hyperparameter tuning, and developing methods that can explain the model’s selection process in a more intuitive and transparent way to enhance user trust and understanding would be valuable contributions.
More visual insights#
More on figures

This figure compares the performance of the cardinality-aware algorithm using two different cardinality cost functions: cost(k) = log k and cost(k) = k. The predictor set K remains consistent across both cost functions ({1, 2, 4, 8}). The results show that the accuracy versus average cardinality curves are very similar for both cost functions across four different datasets (CIFAR-10, CIFAR-100, ImageNet, and SVHN), indicating that the choice of cardinality cost has minimal effect on the algorithm’s overall performance.
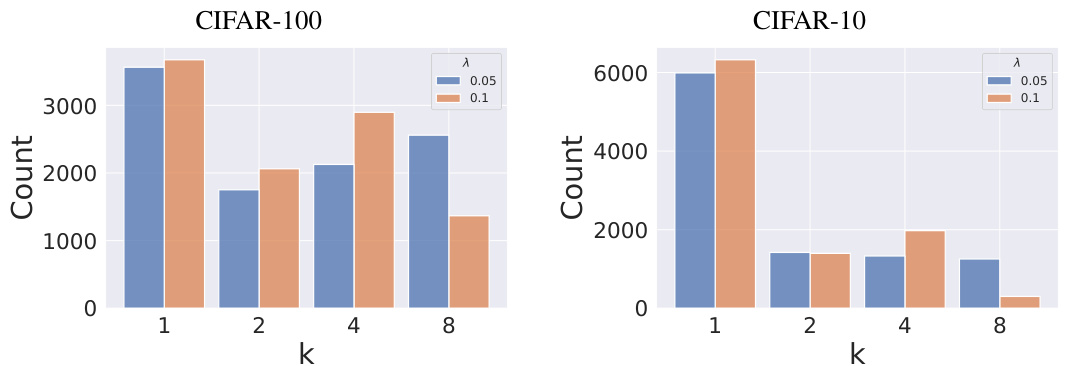
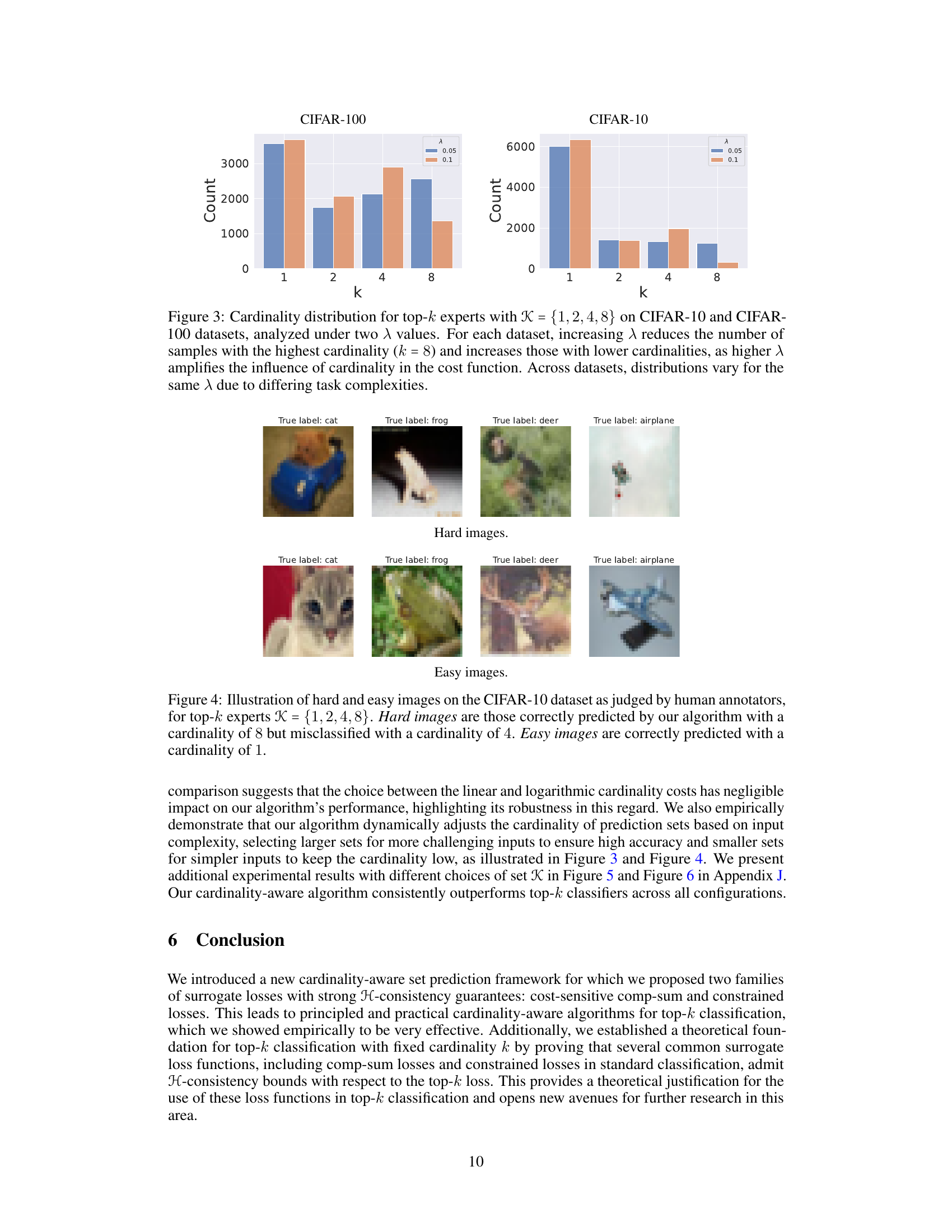
This figure shows the distribution of cardinalities (k) selected by the cardinality-aware algorithm for different values of the hyperparameter λ on the CIFAR-10 and CIFAR-100 datasets. The x-axis represents the cardinality (k), and the y-axis represents the count of samples with that cardinality. Two different λ values (0.05 and 0.1) are shown. Increasing λ makes the algorithm prefer smaller cardinalities, as the cost of higher cardinalities is increased. The distributions also vary slightly between the datasets because of differing complexities of the classification task for CIFAR-10 and CIFAR-100.

This figure shows examples of ‘hard’ and ’easy’ images from the CIFAR-10 dataset, as determined by human evaluators. Hard images are those correctly classified by the cardinality-aware algorithm only when considering the top 8 most likely classes (cardinality =8), but incorrectly classified when considering only the top 4 (cardinality = 4). Easy images are those correctly classified even when considering only the single most likely class (cardinality = 1). This illustrates the algorithm’s ability to dynamically adjust prediction set size based on image complexity.
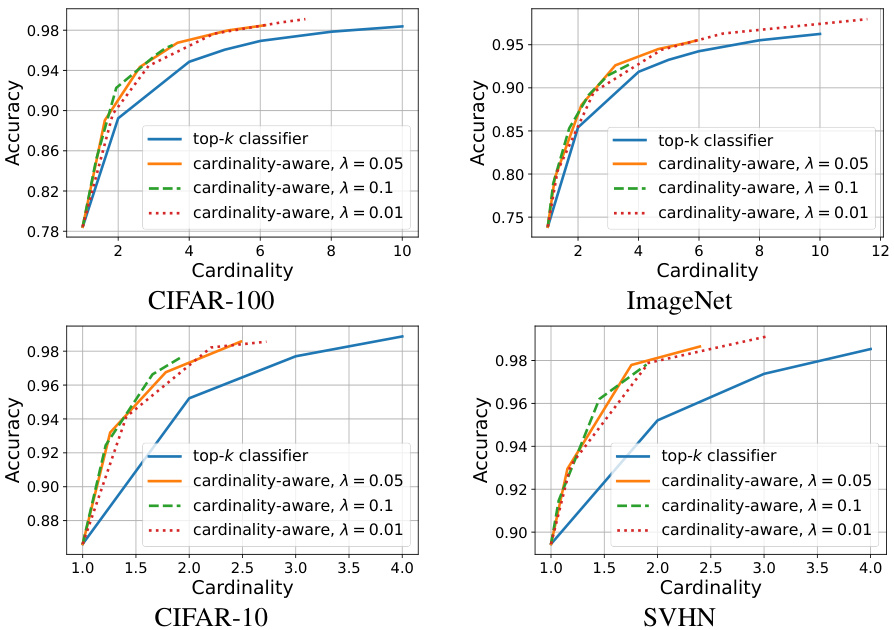
This figure compares the performance of the proposed cardinality-aware algorithm and the standard top-k classifiers in terms of accuracy against the average cardinality of the predicted sets. Four datasets (CIFAR-10, CIFAR-100, ImageNet, and SVHN) are used, and the cardinality cost function is log(k). The results show that the cardinality-aware algorithm consistently outperforms the top-k classifier for any given average cardinality across all datasets.
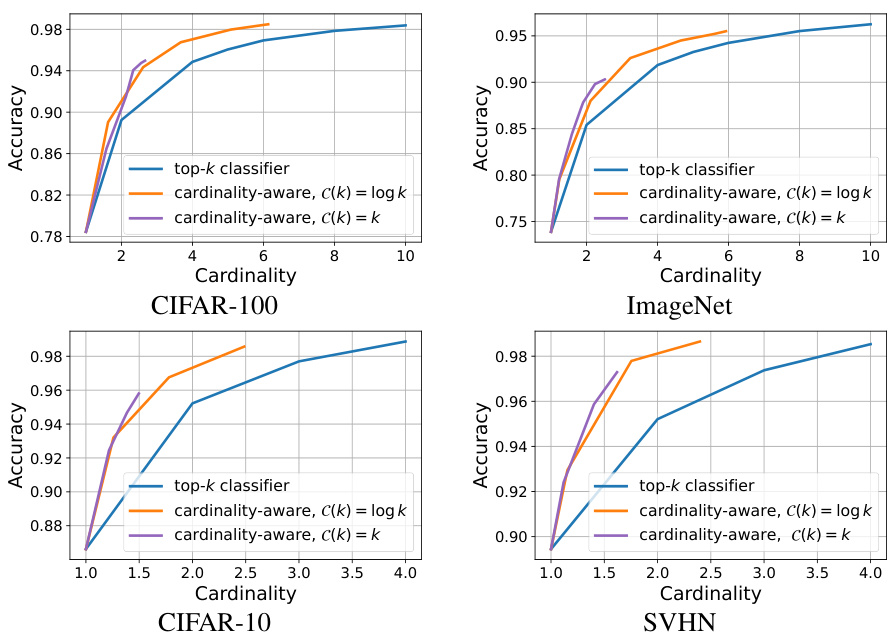
This figure compares the performance of the proposed cardinality-aware algorithm to standard top-k classifiers on four benchmark datasets (CIFAR-10, CIFAR-100, ImageNet, and SVHN). The x-axis represents the average cardinality (k) of the prediction sets, while the y-axis shows the achieved accuracy. Different curves are plotted for various values of the hyperparameter λ in the cardinality-aware loss function. The figure demonstrates that the cardinality-aware algorithm consistently outperforms top-k classifiers across all datasets, achieving higher accuracy for the same average cardinality.
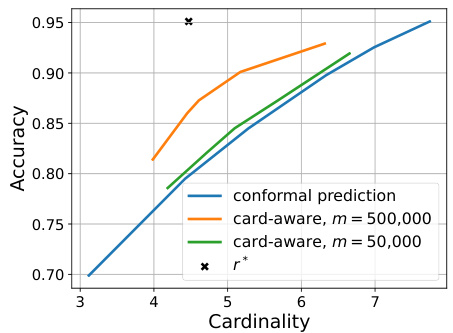
This figure compares the accuracy versus cardinality curves of the cardinality-aware algorithms and conformal prediction on a synthetic dataset. Two curves are shown for the cardinality-aware algorithm, one trained with 50,000 samples and the other with 500,000 samples. The figure also indicates the optimal accuracy-cardinality trade-off point (r*). The results demonstrate that with sufficient data (500,000 samples), the cardinality-aware approach outperforms conformal prediction across all cardinalities. Conversely, with limited data (50,000 samples), the performance gap between the cardinality-aware method and conformal prediction is significantly reduced.

This figure compares the accuracy versus cardinality performance of the proposed cardinality-aware algorithm against conformal prediction on four benchmark datasets: CIFAR-100, ImageNet, CIFAR-10, and SVHN. Each plot shows the accuracy achieved at different average cardinalities. The cardinality-aware algorithm demonstrates improved accuracy compared to conformal prediction across all datasets and cardinalities.
Full paper#