↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Real-time decision-making under constraints is crucial for many applications, such as online recruitment and recommendation systems. Existing methods often struggle with managing multiple constraints or lack theoretical guarantees. This paper introduces II-COS, a novel online sample selection rule. It addresses this by incorporating two types of constraints: individual (e.g., cost and FSR) and interactive (e.g., diversity). The method uses predictive inference to assess the uncertainty in response predictions.
II-COS achieves simultaneous control of both individual and interactive constraints with theoretical guarantees. This is demonstrated through simulations and real-world applications, showcasing superior performance compared to existing methods in scenarios with diverse constraints. The II-COS framework is flexible, model-agnostic, and provides valuable tools for real-time decision-making under diverse practical limitations.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel and flexible online selection rule called II-COS that effectively manages both individual and interactive constraints simultaneously. This addresses a crucial gap in real-time decision-making, particularly in big data applications like online recruitment and recommendation systems. The theoretical guarantees and extensive empirical evaluations make II-COS a valuable tool for researchers and practitioners. It opens new avenues for research into more sophisticated constraint handling and adaptive online selection methods.
Visual Insights#
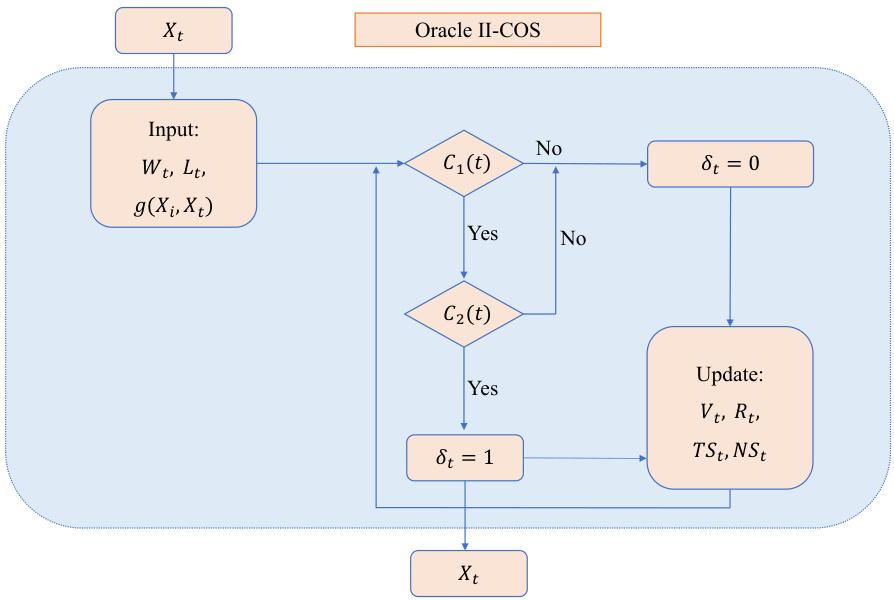
This figure shows the flowchart of the oracle version of the II-COS algorithm. The algorithm takes as input the current sample’s covariates (Xt), a prediction of the response (Wt), and an estimate of the local false discovery rate (Lt). It then evaluates two constraints sequentially: C1(t) which represents an individual constraint and C2(t) which represents an interactive constraint. If both constraints are met, the current sample is selected (δt = 1), otherwise it is rejected (δt = 0). The algorithm then updates internal variables to track the current status of the constraints, and the process repeats for the next sample.

This table presents the results of the II-COS, SAST, and CP methods applied to two real-world datasets: a candidate dataset and an income dataset. It shows the False Selection Rate (FSR), Expected Similarity (ES), and stopping time (Tm) for each method across 500 replications. The target FSR level was 0.2 for both datasets. The target ES level was 1 x 10^-3 for the candidate dataset and 6 x 10^-3 for the income dataset. Standard errors are reported in parentheses.
In-depth insights#
Online Selection Rules#
Online selection rules are crucial for real-time decision-making in scenarios with streaming data. These rules must efficiently balance the need to select the most promising data points while adhering to constraints such as computational cost and desired diversity in the selected subset. Effective online selection rules leverage predictive inference to estimate the value of unobserved data points and guide selection decisions. This allows for a data-driven approach, adapting to changes in data characteristics over time. Key considerations include the type of constraint, which could involve individual constraints (e.g., budget, false positive rate) or interactive constraints (e.g., diversity, similarity), and the design of a stopping rule. The choice of stopping rule affects the algorithm’s performance in terms of efficiency and accuracy; a flexible rule can adapt to varying needs and data characteristics. Ultimately, a well-designed online selection rule balances the competing demands of efficient data utilization and the satisfaction of pre-defined constraints for optimal decision-making.
Predictive Inference#
Predictive inference plays a crucial role in the paper by enabling real-time decision-making under uncertainty. The authors leverage predictive inference to quantify the uncertainty associated with response predictions, which is vital when dealing with unobserved responses. This uncertainty quantification is key to developing a decision rule that effectively controls the false selection rate and other practical constraints. The use of predictive inference is algorithm-agnostic, allowing flexibility in model choice. The effectiveness of this approach is demonstrated through theoretical guarantees and empirical results, highlighting the method’s ability to handle both individual and interactive constraints simultaneously. The integration of predictive inference with constraint control represents a novel contribution, offering a flexible framework for various real-time decision-making scenarios. By carefully quantifying uncertainty, the paper overcomes limitations of existing methods that often neglect prediction uncertainty, which leads to suboptimal sample selection.
Constraint Control#
The effectiveness of real-time decision-making hinges on the ability to select relevant samples while adhering to various constraints. Constraint control in this context involves strategically managing individual and interactive limitations to achieve optimal sample selection. Individual constraints, such as false selection rate (FSR) and cost, focus on the properties of each selected sample. Interactive constraints, however, consider the relationships between selected samples, for example, promoting diversity or minimizing redundancy. The challenge lies in designing a decision rule that efficiently balances these competing constraints and provides theoretical guarantees. This requires a deep understanding of predictive uncertainty to quantify the risk of selecting inappropriate samples and a mechanism for sequentially managing constraints in the online setting. A key contribution is the development of novel methods that quantify uncertainty through predictive inference, providing a rigorous framework for achieving control over both types of constraints simultaneously. Furthermore, model-agnostic approaches enable flexibility in incorporating various algorithms. Theoretical analysis and empirical evidence demonstrate the efficacy of these methods in practical applications like online candidate screening and precision marketing.
II-COS Algorithm#
The II-COS algorithm is a novel online sample selection method designed for real-time decision-making under general constraints. Its core strength lies in its ability to simultaneously manage two types of constraints: individual constraints (such as False Selection Rate and cost limitations) and interactive constraints (like diversity among selected samples). This unified framework addresses the limitations of existing methods that only consider individual constraints. II-COS achieves this by leveraging predictive inference to quantify response prediction uncertainty and sequentially controlling both constraint types, ensuring theoretical guarantees. The algorithm’s model-agnostic nature enhances its flexibility and applicability across various scenarios. Furthermore, the asymptotic guarantees provided demonstrate its effectiveness in controlling both individual and interactive constraints over time. However, it is important to note that II-COS’s effectiveness is highly dependent on the quality of its input predictions and the accuracy of estimated parameters. Furthermore, the selection of appropriate evaluation functions is crucial for effective constraint management.
Future Extensions#
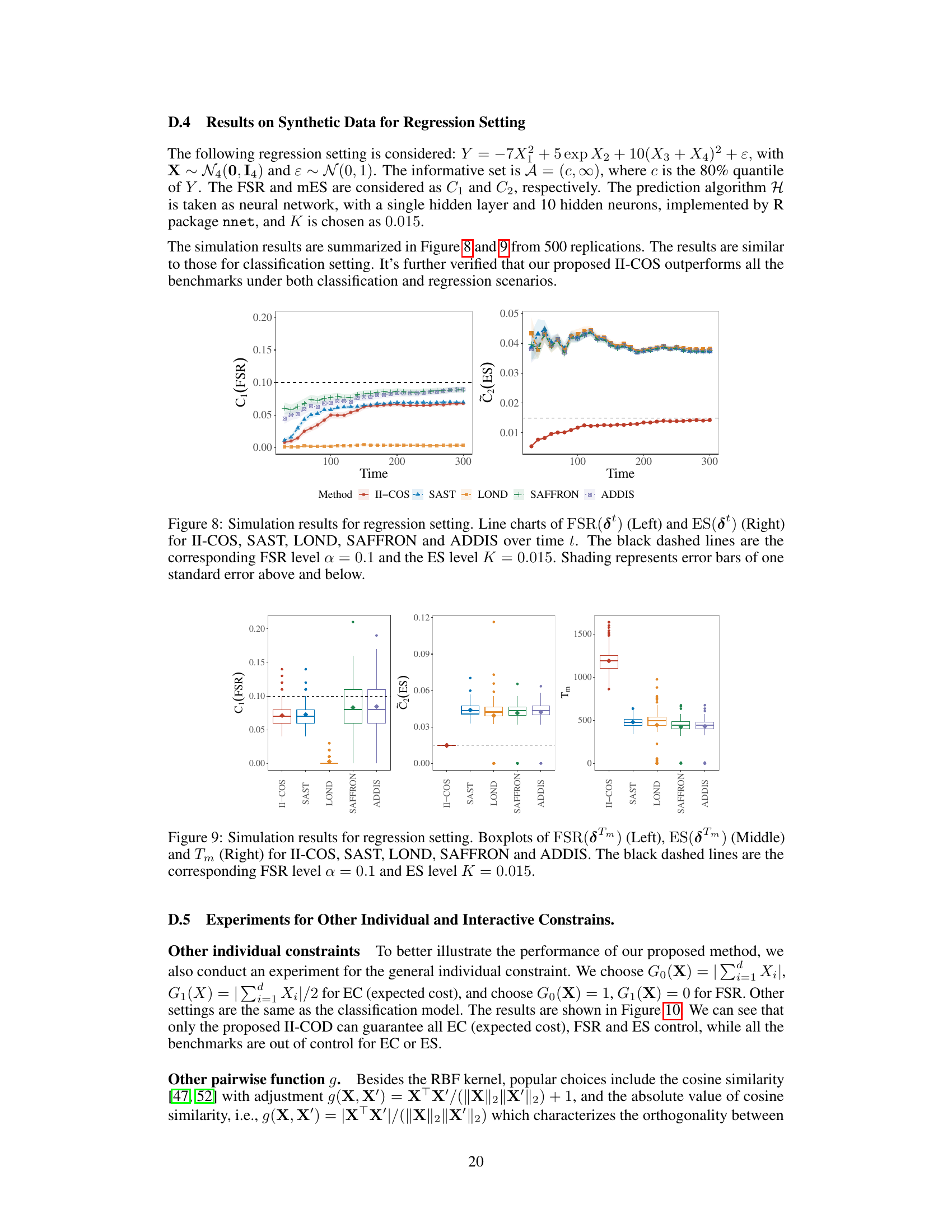
Future extensions of this real-time sample selection research could explore several promising directions. Relaxing the i.i.d. assumption on the data stream is crucial for practical applications, allowing for handling temporal dependencies and concept drift. Incorporating feedback mechanisms would significantly enhance the system’s adaptability and accuracy over time. This feedback could come from human reviewers, user clicks, or other available signals. Investigating different constraint types beyond FSR and diversity would broaden the applicability, including cost optimization, fairness, and specific domain constraints. Exploring the use of more sophisticated prediction models capable of handling complex relationships within high-dimensional data could improve selection accuracy. Finally, developing a comprehensive theoretical framework to analyze the trade-offs between various constraints and their impact on the overall selection efficiency is essential to guide practical algorithm design.
More visual insights#
More on figures
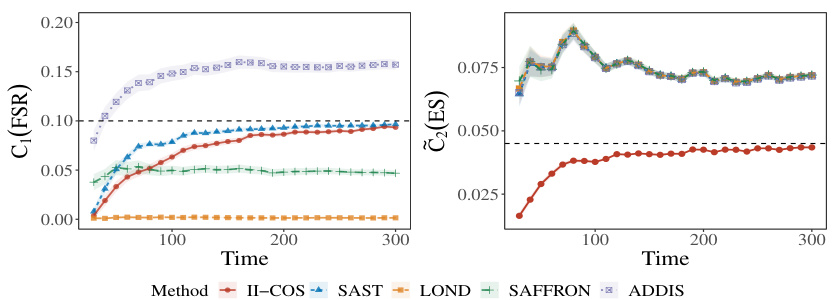
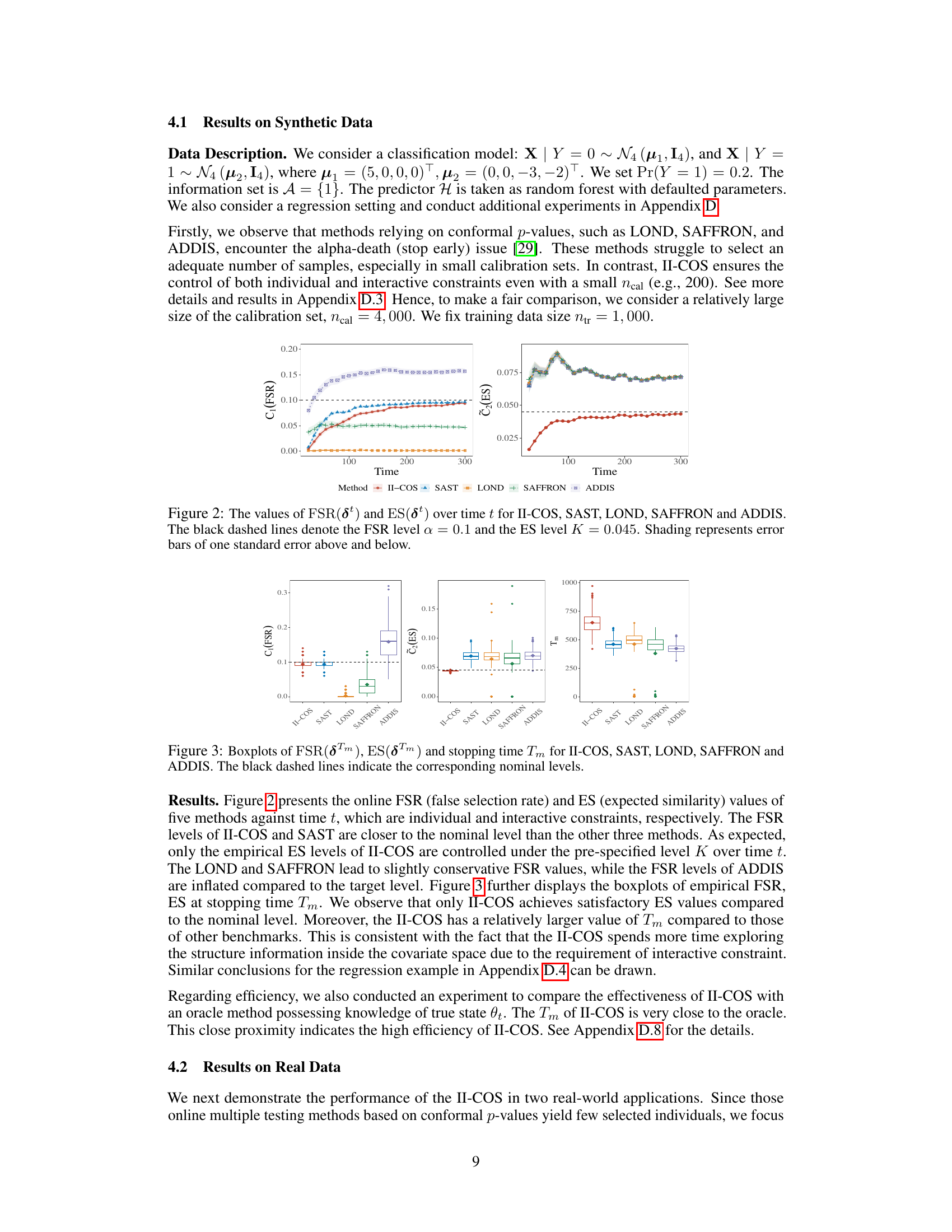
This figure displays the online False Selection Rate (FSR) and Expected Similarity (ES) for five different methods over time. The II-COS method, along with SAST, aims to control both FSR and ES. The other three methods (LOND, SAFFRON, and ADDIS) only focus on FSR control. The dashed lines represent the target levels (α = 0.1 for FSR and K = 0.045 for ES), showing how well each method maintains these constraints. The shaded areas represent error bars, providing a measure of uncertainty in the results.

Boxplots summarizing the results of five methods (II-COS, SAST, LOND, SAFFRON, ADDIS) across 500 replications regarding three metrics: False Selection Rate (FSR), Expected Similarity (ES), and stopping time (Tm). The dashed lines represent the target (nominal) levels for FSR and ES. The figure visually compares the performance of these methods in controlling these two constraints and achieving an efficient stopping time. II-COS shows the closest results to the target levels.
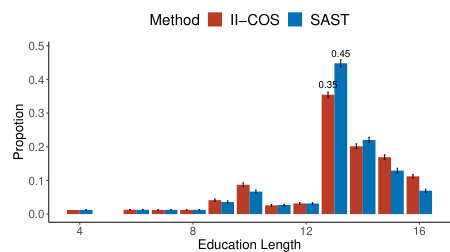
This figure compares the diversity of selected samples by three different methods: II-COS, SAST, and CP, in two real-world applications. The left panel shows the distribution of education levels among the selected candidates in a recruitment dataset. The right panel displays the distribution of education lengths (in years) for selected individuals in an income dataset. Error bars represent the variability across 500 repetitions. The figure demonstrates the superior diversity achieved by II-COS.
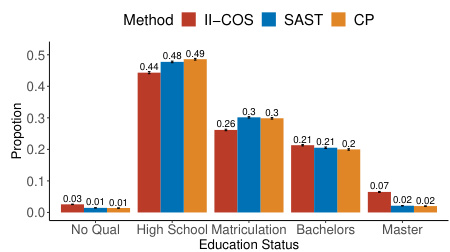
This figure compares the diversity of selected samples by three methods (II-COS, SAST, and CP) across two datasets. The left panel shows the distribution of education status among selected candidates, highlighting the greater diversity achieved by II-COS compared to the other methods. The right panel illustrates the distribution of education length (years) for the income dataset, again showing II-COS promotes more diverse selections.

The flowchart visually represents the steps involved in the oracle II-COS procedure. It starts with an input of Wt and Lt, proceeds to check individual and interactive constraints (C1(t) and C2(t)), and updates parameters based on whether the constraints are satisfied or not. The process iteratively evaluates these constraints for each incoming sample Xt and makes selection decisions (δt=1 for selection, δt=0 for rejection), ultimately generating a selection set.
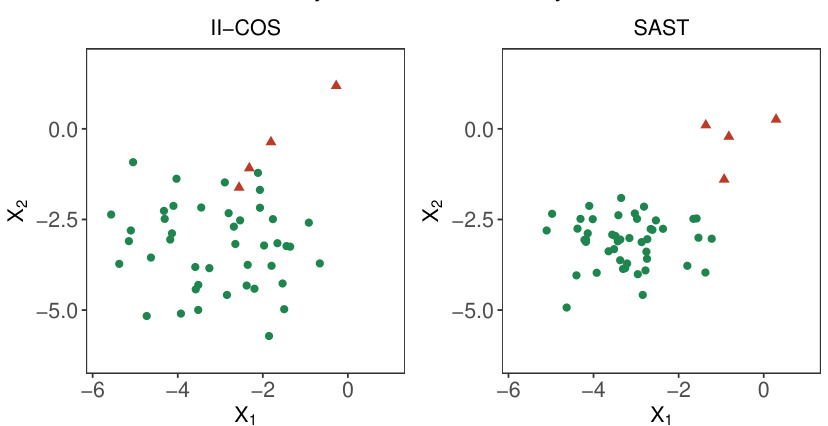
This figure compares the sample selection results of the II-COS and SAST methods. Both methods aim to select 50 samples, but II-COS incorporates both individual and interactive constraints, while SAST focuses only on the individual constraint. The plot shows the first two dimensions of the covariates X for each selected sample. Green dots represent correctly selected samples and red triangles show incorrectly selected samples. The figure demonstrates that II-COS achieves greater diversity across the covariate space and fewer false selections compared to SAST.

This figure shows the online False Selection Rate (FSR) and Expected Similarity (ES) for five different methods (II-COS, SAST, LOND, SAFFRON, ADDIS) over time. The dashed lines represent the target levels for FSR (α = 0.1) and ES (K = 0.045). The shaded areas indicate the standard error of the mean for each method. The figure demonstrates the ability of the II-COS method to control both FSR and ES effectively compared to other methods.
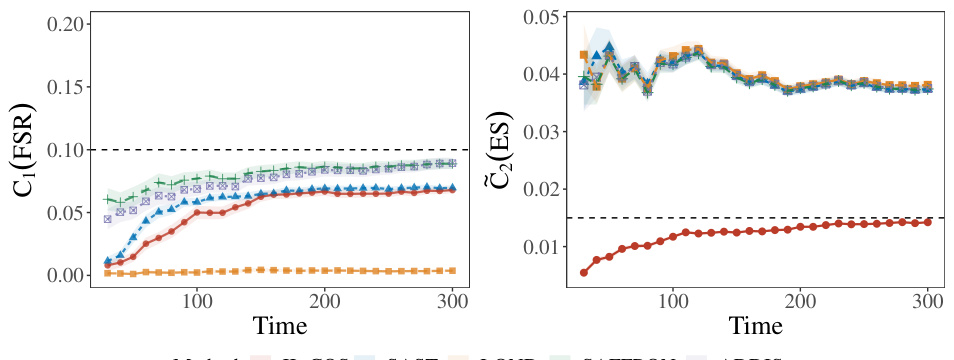
This figure displays the online false selection rate (FSR) and expected similarity (ES) over time for five different online sample selection methods: II-COS, SAST, LOND, SAFFRON, and ADDIS. The II-COS method aims to control both individual and interactive constraints simultaneously. The black dashed lines represent the target FSR level (α = 0.1) and ES level (K = 0.045). Shaded regions indicate the standard error around the mean for each method. The results illustrate the ability of II-COS to maintain these constraints over time, in contrast to other methods.

This figure compares the performance of five different online sample selection methods (II-COS, SAST, LOND, SAFFRON, and ADDIS) across three key metrics: False Selection Rate (FSR), Expected Similarity (ES), and stopping time (Tm). Box plots visually represent the distribution of each metric across multiple simulation runs. The black dashed lines indicate the pre-specified target levels for FSR and ES. This figure allows for a direct visual comparison of the effectiveness of different methods in controlling both individual (FSR) and interactive (ES) constraints while maintaining efficiency (Tm).

Boxplots comparing the performance of II-COS and four benchmark methods (SAST, LOND, SAFFRON, ADDIS) across three metrics: Expected Cost (EC), False Selection Rate (FSR), and Expected Similarity (ES). The black dashed lines represent the target levels for each metric, demonstrating II-COS’s ability to control all three simultaneously.
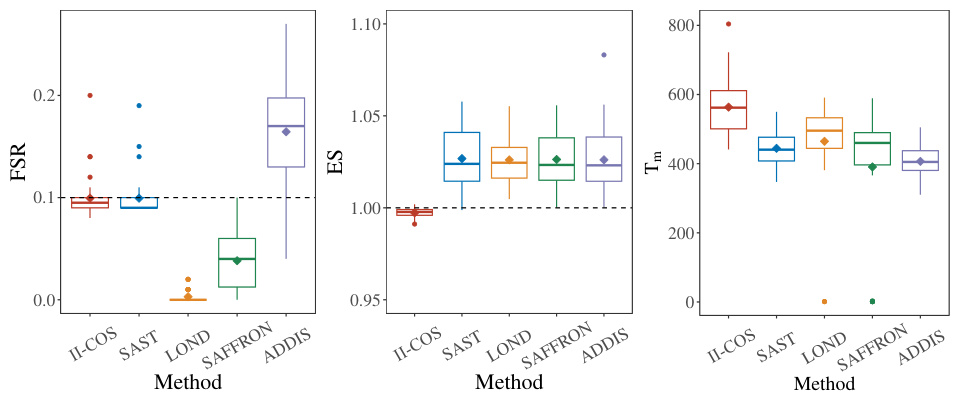
This figure displays boxplots summarizing the performance of five different online sample selection methods: II-COS, SAST, LOND, SAFFRON, and ADDIS. Each method’s performance is evaluated across three metrics: False Selection Rate (FSR) at the stopping time (Tm), Expected Similarity (ES) at Tm, and the stopping time Tm itself. The black dashed lines represent the target or nominal levels for FSR and ES, providing a visual comparison of how well each method achieves its goals. The boxplots visually represent the distribution of results from multiple replications, showing the median, quartiles, and potential outliers.
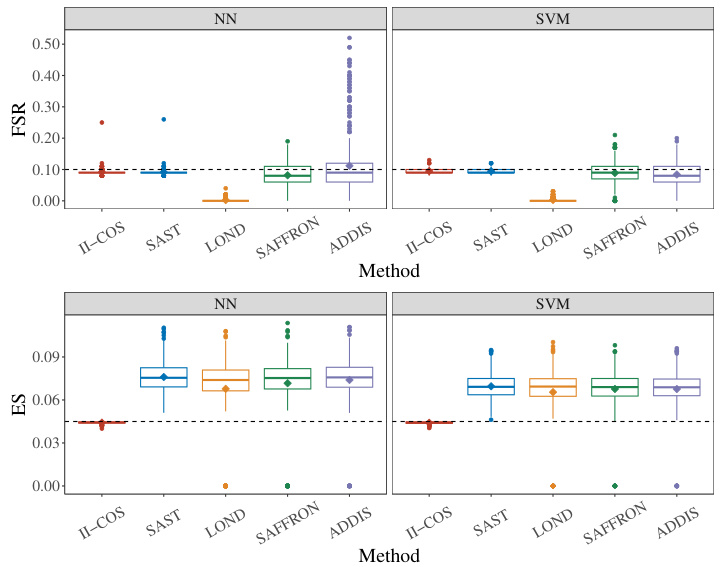
This figure compares the performance of II-COS against four other online FDR control methods (SAST, LOND, SAFFRON, ADDIS) using two different learning algorithms (NN and SVM). It shows the boxplots of the False Selection Rate (FSR), Expected Similarity (ES), and stopping time (Tm) for each method. The black dashed lines indicate the target levels (α = 0.1 for FSR, K = 0.045 for ES). The figure illustrates the II-COS method’s ability to effectively control both individual and interactive constraints, while the other methods struggle, particularly in controlling the ES.
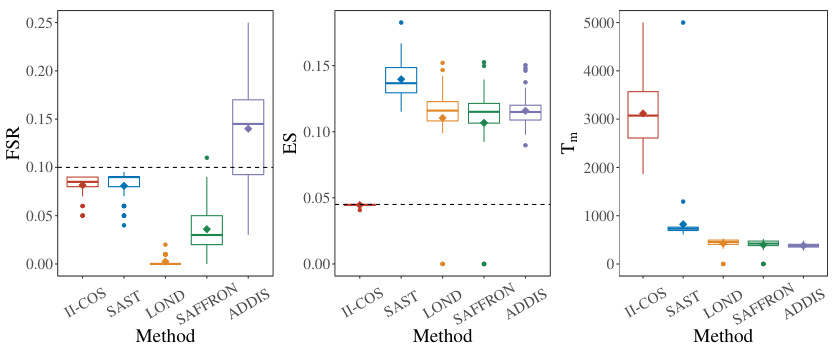
This figure compares the performance of II-COS against four other online multiple testing methods (SAST, LOND, SAFFRON, ADDIS) in terms of False Selection Rate (FSR), Expected Similarity (ES), and stopping time (Tm). Boxplots show the distribution of these metrics across 500 simulation runs. The dashed lines represent the target levels for FSR and ES. The results demonstrate II-COS’s effectiveness in controlling both individual (FSR) and interactive (ES) constraints while maintaining efficiency (Tm).
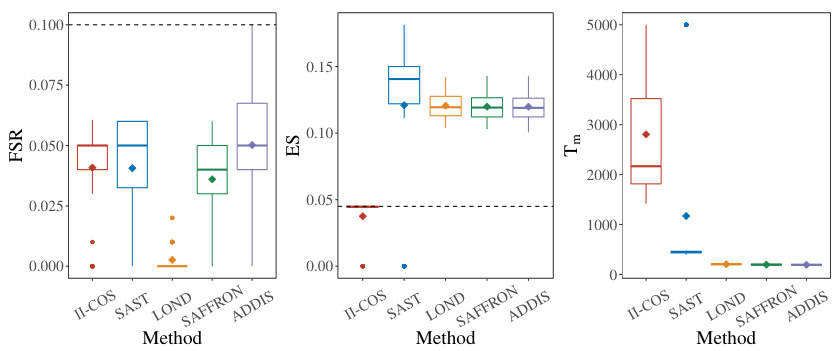
This figure compares the performance of five different methods (II-COS, SAST, LOND, SAFFRON, and ADDIS) in terms of three key metrics: False Selection Rate (FSR), Expected Similarity (ES), and stopping time (Tm). Boxplots show the distribution of these metrics across 500 replications. The dashed lines represent the target values for FSR and ES. The figure helps assess the effectiveness of each method in controlling both individual and interactive constraints while maintaining efficiency (measured by stopping time).
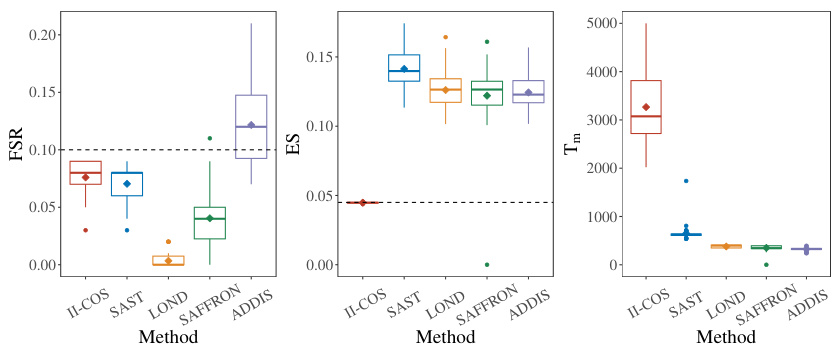
This figure compares the performance of five different methods (II-COS, SAST, LOND, SAFFRON, and ADDIS) in terms of three metrics: False Selection Rate (FSR), Expected Similarity (ES), and stopping time (Tm). Boxplots illustrate the distribution of each metric across 500 replications. Dashed lines represent the target levels for FSR and ES. The figure shows that II-COS effectively controls both FSR and ES while maintaining relatively longer stopping times, indicating better performance in balancing constraint satisfaction with sample selection efficiency.
More on tables

This table compares different methods for controlling the False Discovery Rate (FDR), both offline and online. It shows the formulas used for estimating the False Discovery Proportion (FDP) for each method, highlighting the key differences in how they adjust for multiple testing in offline versus online settings. The offline methods are Storey-BH and BH, while the online methods are LOND, SAFFRON, and ADDIS. The formulas illustrate how each method dynamically adapts its thresholds for rejecting hypotheses, balancing the trade-off between controlling the FDR and maximizing the number of true discoveries.
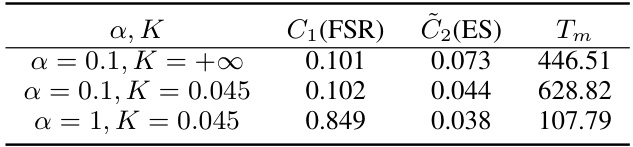
This table shows the results of an experiment to illustrate the flexibility of the II-COS procedure in terms of adjusting the individual and interactive constraint levels. It presents the average false selection rate (FSR), expected similarity (ES), and stopping time (Tm) for different combinations of α and K, which represent the individual and interactive constraint levels respectively. By changing these parameters, one can control the trade-off between the two types of constraints and stopping time.

This table presents a comparison of the number of samples selected by the II-COS method and three other online FDR control methods (LOND, SAFFRON, ADDIS) under different calibration sizes (ncal) in both classification and regression settings. The stopping rule is to select m=100 samples. The results show that II-COS consistently selects the target number of 100 samples, unlike the other methods which often select fewer samples, especially when the calibration size is small. The under-selection is more prominent in the regression setting than in the classification setting.

This table presents the average values of the False Selection Rate (FSR) and Expected Similarity (ES) at the stopping time Tm for the II-COS method under different calibration sizes (ncal). It shows the performance of II-COS in controlling both individual and interactive constraints for both classification and regression settings when the calibration set size varies from 200 to 800. The results demonstrate that II-COS effectively maintains the FSR and ES levels across different calibration sizes.

This table presents the results of the II-COS, SAST, and CP methods on two real-world datasets: a candidate dataset and an income dataset. The table shows the average values (across 500 repetitions) for the False Selection Rate (FSR), Expected Similarity (ES), and stopping time (Tm) for each method on each dataset. The target FSR level (α) is 0.2 for both datasets, but the target ES level (K) differs: 1 x 10^-3 for the candidate dataset and 6 x 10^-3 for the income dataset. Standard errors are included in parentheses for each value.

This table presents the results of comparing the proposed II-COS method with an oracle method which knows the true state 0t in advance. The experiment is conducted under a classification setting. The table shows the False Selection Rate (FSR), Expected Similarity (ES), and the stopping time (Tm) for both II-COS and the oracle method. The oracle method serves as a benchmark for evaluating the efficiency of II-COS.
Full paper#